基于DWT-LPP的行星变速箱故障信号特征增强方法

江鹏程， 丛 华， 吴春志， 冯辅周

(陆军装甲兵学院车辆工程系， 北京 100072)

行星变速箱作为某型装甲车辆传动系统的重要组成部分，具有较大的传动比和较高的承载能力，在其他军用装备中得到了广泛的应用[1-2]。行星变速箱工作条件恶劣，齿轮容易发生磨损、点蚀甚至是断裂等故障[3]，这将严重影响装备的机动性能，造成传动箱二次损伤，进而增加维修费用[4]。根据系统传动特性，当齿轮发生故障时，通过测取振动信号可以检测行星变速箱的状态。然而，齿轮故障信号在传递时，容易与其他多种激励源产生噪声混叠，使得传感器采集到的信号具有较强的非线性和非平稳性[5]。因此，传统的信号处理方法很难有效提取对行星变速箱的故障。

信息熵是对系统不确定性的描述。近年来，样本熵(Sample Entropy,SE)、排列熵(Permutation Entropy,PE)和功率谱熵(Power Spectrum Entropy,PSE)等被越来越多地运用到机械设备的故障诊断中[6-8]。然而，行星变速箱的信号复杂，直接计算信息熵无法对信号直接分类。局部保持映射算法(Locality Preserving Projection，LPP)是机器学习算法的一种，与典型的流形学习算法不同，LPP可以将高维的信号进行降维处理，在保留信号的空间局部流形特征的同时，发掘信号的隐藏信息[9-10]。此外，离散小波变换(Discrete Wavelet Transform，DWT)可对信号进行无冗余重构和精准重构，并将故障信号按频带严格区分开来。

基于此，笔者提出一种基于DWT-LPP的行星变速箱特征增强方法。首先，利用DWT对信号进行多频带分解重构；然后，采用LPP对得到的高维信号进行降维处理，突出故障特征；最后，计算信号的信息熵值，并通过三维信息熵坐标实现故障信号的有效区分。

1 相关原理

1.1 离散小波变换

离散小波变换(DWT)是信号在时频域中的一种多尺度分解运算，其作用是将信号从一维扩充到高维，其算法的核心为Mallat算法。对信号进行小波分解的过程为：首先，通过高通滤波器和低通滤波器对信号进行采样，得到第1层高通系数D1和低通系数A1；然后，再次通过高通滤波器和低通滤波器对系数D1、A1重构得到信号进行采样；最后，对得到的重构信号进行循环采样和重构，并最终得到不同层高低不同频段的信号。图1为Mallat算法流程。

求解过程如下：

Ac+1(k)=∑bAc(b)H(b-2k)；

(1)

Dc+1(k)=∑bAc(b)G(b-2k)。

(2)

式中：c为层数；b为各层系数长度；k为各层系数序列点。

1.2 局部保持映射算法

局部保持映射算法(LPP)是通过线性过程来近似地求取算子，以实现对数据的线性维数约减。该算法克服了主成分分析法难以使数据保持非线性流形结构的不足，可在不改变数据局部流形结构的前提下，实现信号在映射空间的特征增强[11]。局部保持映射算法是一个对数据映射的优化过程[12]：对于数据X=(X1,X2,…,Xn)∈RD×n，求映射f:RD→Rd，得到目标矩阵Y=(Y1,Y2,…,Yn)。局部保持映射算法就是求取一个映射矩阵W，使得Y=XW，其中W的目标函数为

(3)

式中：Xi,Xj均为原始数据样本；sij为权重系数，由K-近邻法构造近邻图计算，来表示数据样本之间的相似度。即

(4)

式中：β为所有样本之间欧氏距离均值的平方。

式(3)经过运算可得

(5)

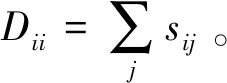
XLXTW=λXDXTW

(6)

的广义特征向量得到。

1.3 信息熵

信息熵是由信息论之父香农于1948年提出的[13]。信息熵是指信息论中信息无序度的度量，即信息熵与信息的无序度成正比，与信息的效用值成反比。因此，系统中的信息效用值可以用信息熵来衡量。通过振动信号提取的信息熵可以反映行星变速箱的振动状态[14]。

1.3.1 排列熵

排列熵是一种衡量一维信号复杂度的平均熵参数，具有计算简单、抗噪能力强等特点，对于信号中的突变情况具有较强的检测能力。

对信号X=(x1,x2,…,xN)进行相空间重构，得到重构矩阵

(7)

式中：Bl(l=1，2，…，K)为第l个重构分量，其中K+(m-1)τ=N；m为嵌入维数；τ为延迟时间。将重构矩阵B中的任一重构分量中的元素按照由小到大的顺序重新排列。由于重构矩阵中重构分量为m维向量，因此对应的位置索引序列最多有m!种。设重构矩阵中所有重构分量实际对应的位置索引序列为K′种，则有K′≤m!。

统计并计算重构矩阵中所有重构向量的每一种位置索引序列出现的概率p1,p2,…,pl′,…,pK′，其中pl′=Cl′/K′,Cl′为第l′种位置索引序列出现的次数。根据信息熵的数学模型，重构分量对应的K′种不同位置索引序列的排列熵定义为

(8)

1.3.2 样本熵

样本熵可以有效衡量振动信号的复杂度，与信号的复杂度成正相关。其计算流程如图2所示。

图2 样本熵计算流程

样本熵的计算公式为

(9)

式中：q=1,2,…,Q,为模式维数；r为相似容限;Bq(r)和Bq+1(r)分别为模式维数在q和q+1下的平均长度。参考文献[6]，取q=2，r=信号的标准差。

1.3.3 功率谱熵

功率谱熵是从频域角度定义的信息熵，用来度量信号在频域上的复杂度,是一种信号在频域上的划分规则，其定义为

山塘涵洞长度普遍较短，可根据施工图设计在地面上初步拟定钻孔走向，然后用仪器测定进出口平面位置和高差，依据洞轴线长度和高差计算钻孔纵坡，确定钻孔偏角，根据纵坡和偏角调整钻杆入岩角度，完成后即可开始钻进施工。钻进施工过程在导向仪的指引下，及时调整和修正钻头钻进方向，确保导向孔按设计顺利成孔。

(10)

式中：qo为信号功率谱归一化后的重构矩阵中所有重构向量的每一种位置索引序列出现的概率；P为重构向量个数。

1.4 算法流程

DWT-LPP是一种结合离散小波变换(DWT)和局部保持映射算法(LPP)的数据处理方法，其算法处理过程为：1)对采集到的振动信号进行离散小波变换，将一维信号扩展到多种频域尺度的多维信号矩阵；2)对矩阵进行局部保持映射降维，得到保持信号局部流形结构信息的映射结果；3)采用相关信息熵提取特征值，完成故障分类诊断。算法处理流程如图3所示。

由于齿轮断齿的故障频率主要在低频段，高频部分主要是衰减的倍频成分、相关实验设备以及齿轮箱运行过程中产生的噪声。因此，采用DWT-LPP算法可以降低与故障信号相关度低的高频部分信号能量占比，进而使故障信号的特征得到增强，从而更好地实现故障的分类诊断。

2 实验设计

行星变速箱故障实验台实物图和原理图如图4所示。图中：实验台的机械驱动装置由变频电机、发电机、传动箱、行星变速箱、液压站和转速扭矩仪等组成。其中：发电机、传动箱的功能是改变力的传递方向，使实验台的整体布局合理；行星变速箱两侧的输出端连接到转速扭矩仪，转速扭矩仪由发电机加载；液压站负责在行星变速箱上提供润滑油压力和换挡压力。实验设定了4种故障状态，即K1和K3排的太阳轮断裂故障(K1-30断齿和K3-31断齿)和与太阳齿轮啮合的行星齿轮的断齿故障(K1-15断齿和K3-18断齿)。断齿故障设置如图5所示。

测试系统设备包括主控制平台、32通道信号采集设备、振动传感器和相应的数据线。主控制平台控制行星变速箱故障模拟实验台的启动和停止、速度调节、加载扭矩和其他过程。振动传感器采用DYTRAN公司的127-3023M2型传感器，信号采集仪的通道采用东华数据采集软件设置。设置采样频率为20 kHz，采样时间为30 s，分别采集1-5挡以及倒挡时的数据。本次实验选用3挡时转速1 500 r/min和900 N·m负载的数据作为测试数据，测点位置为箱体内部，K2行星排内齿圈上方。

3 数据分析与处理

3.1 实验数据分析

由于行星变速箱工作状态复杂，噪声干扰严重，因此对于内部不同位置的断齿故障，很难从原始信号的时域图中区分。图6为行星变速箱齿轮正常以及4种断齿故障下采集到的振动信号。本次实验所选信号样本长度均为4 800点，大于2倍周期，采样时间为0.24 s，每种状态各取100个样本。

3.2 DWT-LPP处理

对采集到的各个状态的信号首先进行离散小波变换(DWT)，选用“db5”小波基进行3层小波变换。以K1-15断齿信号为例，重构a1、a2、a3三个低频分量以及d1、d2、d3三个高频分量的信号，重构信号各分量的时域图如图7所示。

将图7(a)-7(f)的分量信号进行局部保持映射变换(LPP)，得到的降维信号的时域图如图8所示。对比图8、6(b)可以发现：K15断齿信号在经过DWT-LPP处理后，信号形态更加稳定。

图9为DWT-LPP处理前后K15断齿信号的频域图，可以看出：经处理后，信号在高频噪声部分得到了抑制，在低频部分信号得到了增强。

3.3 信息熵特征增强

通过计算DWT-LPP处理后5种状态各100组信号的信息熵值，得到以功率谱熵、排列熵和样本熵为坐标的三维图，如图10所示。各状态信号DWT-LPP处理前后信息熵均值和方差如表1所示。通过对比可以发现：经处理后，行星变速箱各故障状态信息熵值类间差别得到了增强，方差减小。这说明：经DWT-LPP处理可使信息熵的类内聚焦性和类间离散性明显增强。

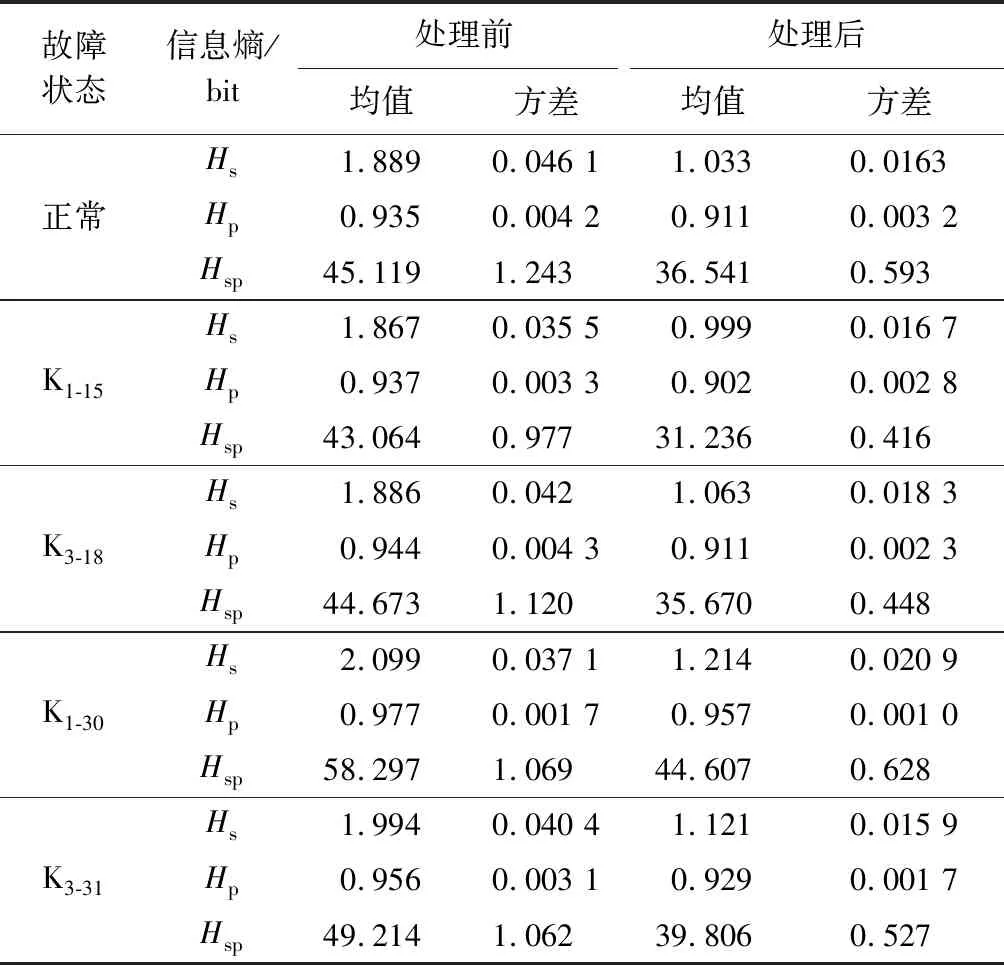
表1 各状态信号DWT-LPP处理前后信息熵均值和方差

4 结论

针对行星变速箱齿轮故障振动信号故障特征微弱，容易被噪声湮没，直接采用排列熵、样本熵、功率谱熵等信息熵进行故障分类难以诊断不同故障状态的问题，提出了一种基于离散小波变换和局部保持映射相结合的故障信号特征增强算法，降低了高频噪声的影响，增加了主要频率信号的能量，增强了信息熵的类间差异性。主要结论如下：

1) 离散小波变换能够在时频域内对信号进行多频率段提取重构，可以实现信号的频带多尺度化。

2) 局部保持映射算法能够保持数据的流形结构，可以对多维信号进行降维处理，与离散小波变换增强了信号的稳定性，降低了噪声干扰。

3) 多种信息熵能够反映行星变速箱不同齿轮的故障状态，用DWT-LPP处理后增强了信息熵的类内聚焦性和类间离散性，有助于齿轮故障的诊断与分类。