基于列生成算法的无人机任务分配
李瑞阳 王智学 何红悦 邓巧雨
1.陆军工程大学指挥控制工程学院江苏南京210000
无人机是一种无需人员驾驶的空中飞行器,能够实现自主飞行、独立地完成作战任务,因此,逐步成为执行多样化军事任务的最佳选择[1−2].无人机任务分配问题是根据既定目标,把需要完成的任务合理地分配给系统中的成员,达到高效率执行任务,优化无人机系统的目的[3−4].该问题本质上可以看作车辆路径规划问题,主要从建立数学模型和算法求解两方面入手进行研究.
在以往对于任务分配问题求解算法的研究中,绝大多数文献都是采用人工智能算法进行求解,这类算法虽然操作简单,易于实现,但是很难保证收敛到全局最优解[5−9],而列生成算法、拉格朗日松弛算法这类的基于数学规划的启发式算法克服了这些缺点,从理论上讲,不受规模限制,能收敛到最优解,属于精确性方法,目前国内外有很多学者将其应用于求解各种条件下的优化分配问题[10−14],但是考虑时间窗约束条件下的无人机任务分配调度问题,目前的研究还比较匮乏,本文基于具体的无人机运输任务,利用列生成算法建模求解,旨在找到运输任务分配的最佳方案,为指导作战实践提供参考.
1 问题描述
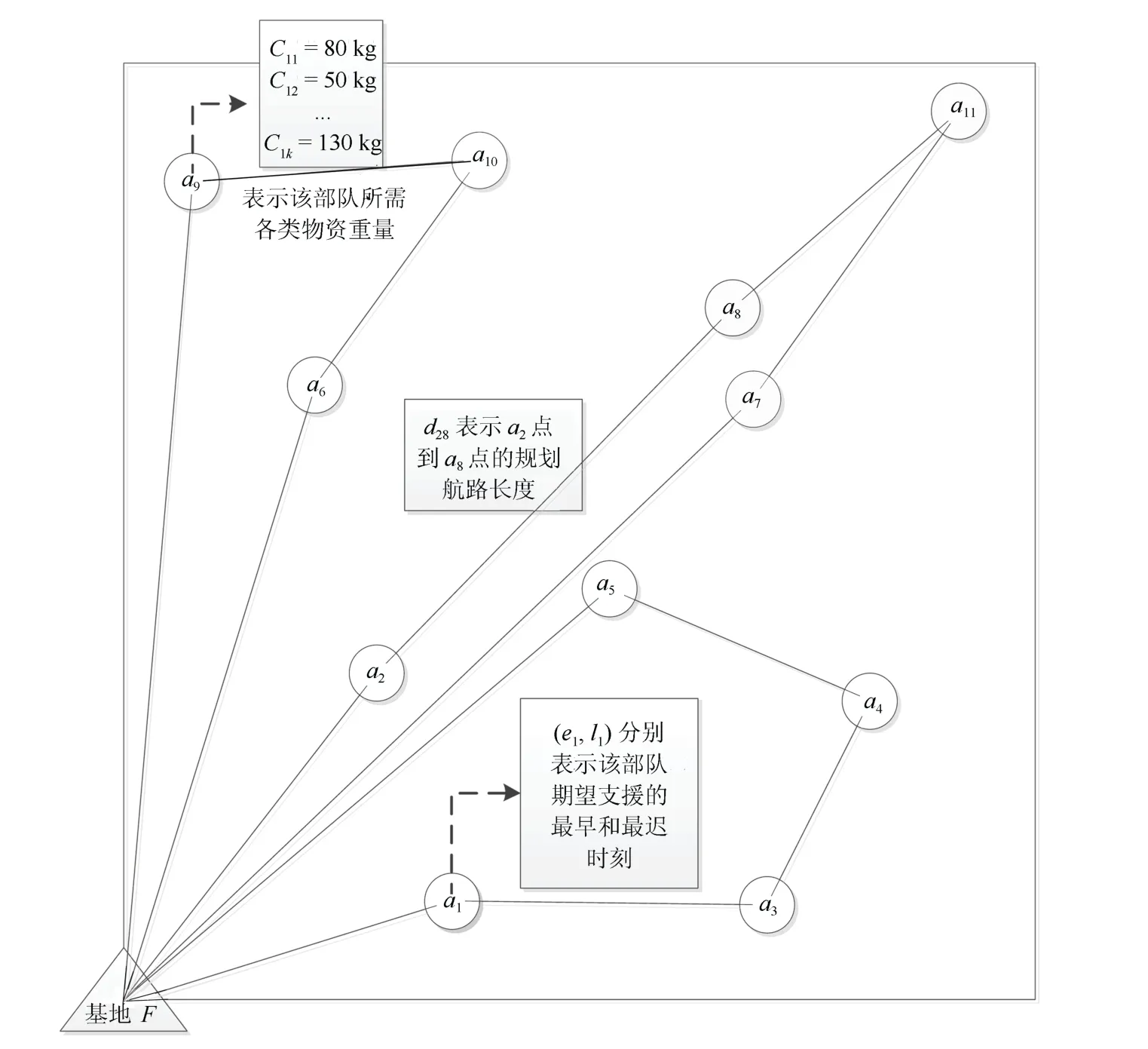
在无人机运输任务分配问题中,如图1所示,敌我双方的交战地域S=[0,s]×[0,s]内,有n支我军部队A={a1,a2,··· ,an}正在等待物资补给,需要从某基地F调派一定数量的无人机U={U1,U2,··· ,Um}完成所有部队的支援任务.
任务开始前,假设我军已经通过侦察机获取了所有目标部队以及交战地域内敌人防空阵地的地理坐标,采用航路规划技术规划了任意两点之间的优化路线,准备为各无人运输机进行任务分配.每个目标部队所需要的物资重量事先已知,表示为C={C1,C2,··· ,Cn},部队ai期望得到补给的时间范围表示为(ei,li),每架无人运输机的任务可以表示为一组目标部队的有序集合,如TaskU1={F→ai→··· →aj→F},规划派出无人机数量最少,飞行路程最短的分配方案,完成所有部队的任务需求.
2 数学模型
2.1 模型假设
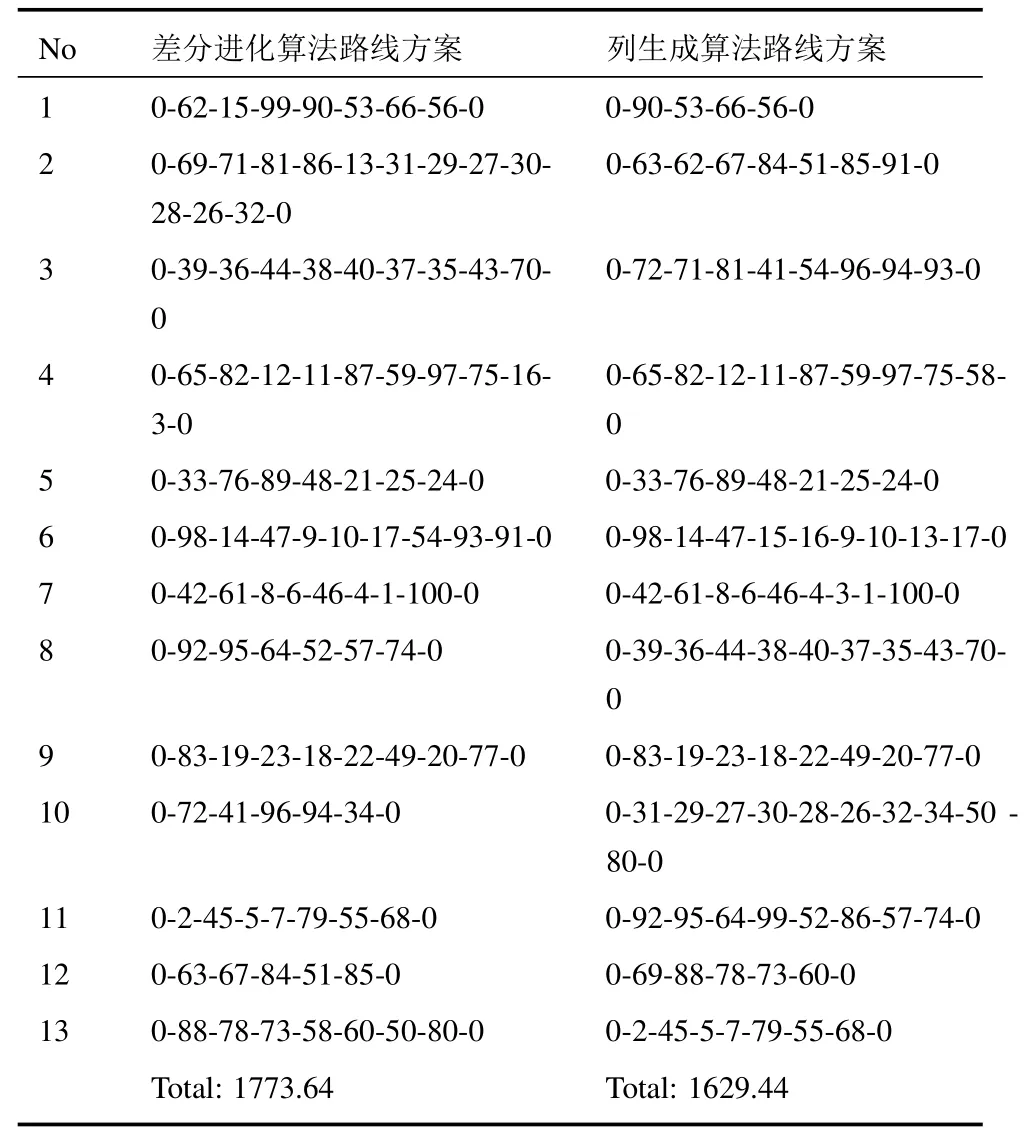
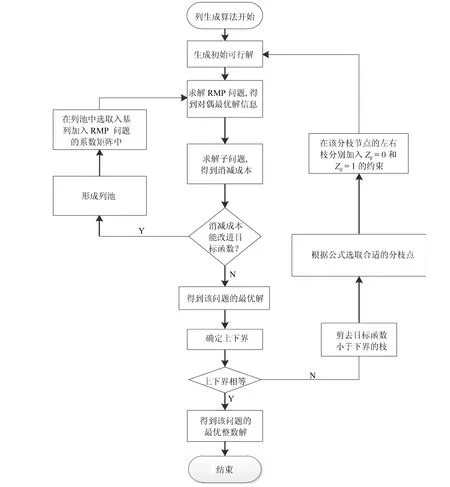
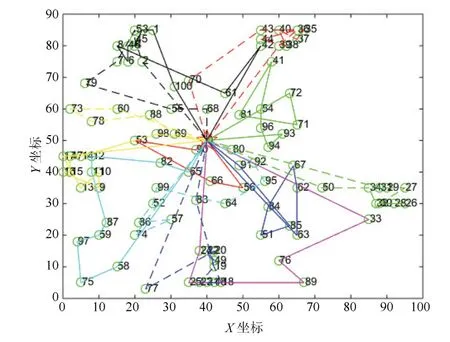
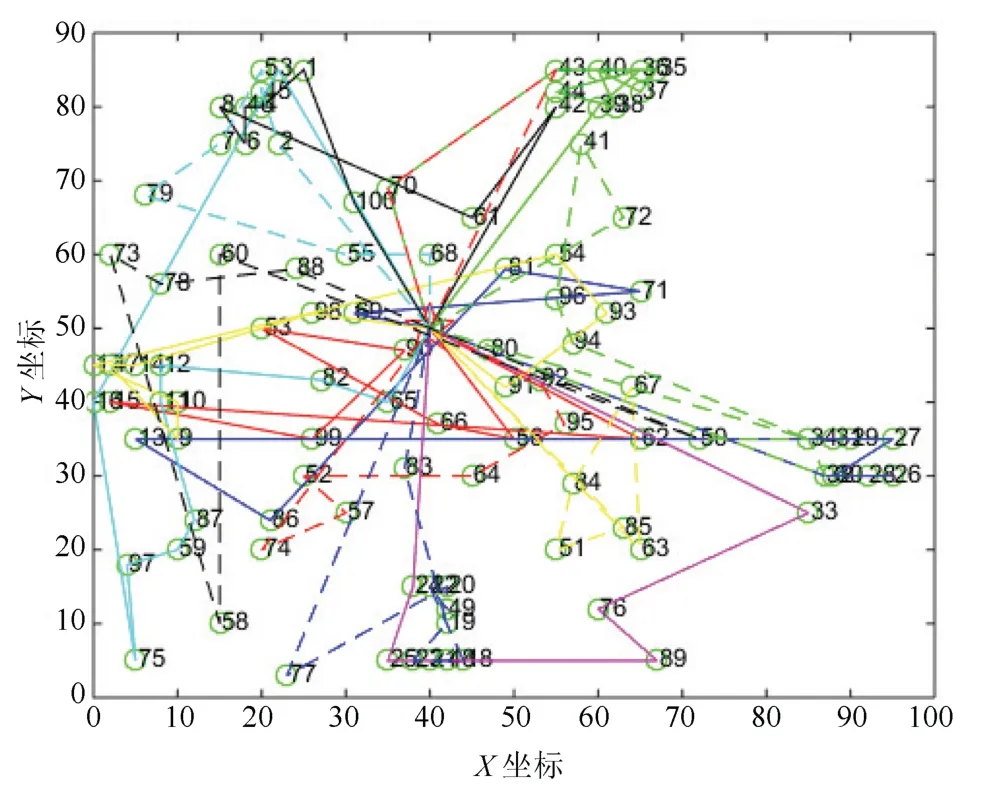
正如图1所示,无人机运输任务分配问题的基本模型可以看作一个完全无向图G=(V,E),其中V=(a0,a1,··· ,an)是运输网络中节点的集合,a0=F表示出发基地,其余表示n支等待支援的作战部队;E={dij,(i 1) 每架无人机从后勤基地出发,沿着某一条飞行路线把所装载的所有物资补给运输给待支援部队后,返回原基地; 2) 每架无人机可以为多支部队提供补给,但是为了避免多架无人机在空中飞行时发生碰撞事故,每只目标部队只安排一架无人运输机进行支援; 3) 每架无人机的载重量是有限制的,所运载的物资补给总重量不能超过该范围.为了简化问题,假设所有无人运输机型号相同,拥有相同的载重能力,同时不考虑物资种类对飞行的影响; 4)不考虑无人运输机在各个目标部队位置处的转向角约束,也不考虑无人运输机的航程约束; 5) 假设每支部队都会进行战前预估,都有接受补给的时间窗,即部队对于补给物资的到达时间要求是在某个时间段上的. 2.2.1 标号和参数变量 U表示无人运输机的集合;A表示待援部队的集合;V表示任务分配模型网络中的节点集合,由后勤基地与待援部队共同组成,将基地拓展为出发以及接收节点,分别标为0 和n+1 号节点,待援部队构成了1 到n号节点;cij表示网络中任意两个节点i和j构成的弧(i,j)上的飞行路线成本,等价于两点之间飞行路线的长度dij表示;tij表示网络中任意两个节点上的飞行时间;Ci表示部队的物资需求;q表示每架无人机的最大载重量;[ei,li]表示每个节点的服务时间窗要求.sik表示无人运输机k在节点i的卸载物资开始时间;xijk表示0 −1 变量,如果无人机k经过弧(i,j),则为1,否则为0. 图1 无人机运输任务分配示意图 2.2.2 数学模型 无人机运输任务分配的数学模型可以表示为: 其中,式(1)是问题的优化目标,表示执行任务的总成本最小,式(2)表示无人机从起点出发,只能选择一条路线,每只部队只能被一架无人机支援; 式(3)表示无人运输机的实际载货量不能超过其最大限制容量;式(4)∼式(6)共同构成网络的流约束,表示每架无人机从基地出发,经过待援部队处不停留,并最终返回基地.式(7)表示如果无人运输机经过弧,那么车辆在点开始卸载物资的时间约束.式(8)保证了在每个点开始卸载物资的时间要满足该点的时间窗约束.式(9)是整数约束.可以看出,其中式(7)是非线性的,引入式(10)替代将其转化为线性约束: 其中,M代表一个足够大的数. 列生成算法是一种基于数学规划的启发式算法,适合于求解大规模线性规划问题.算法受Dantzig 和Wolfe 提出的著名的块对角结构与Dantzig-Wolfe 分解原理启发[15]而设计产生的.其基本原理是: 将原始线性规划问题中分成两个部分,即限制性主问题(RMP)和子问题(SP),其中RMP 中含有m个决策变量,用于生成基可行解,使用单纯形法对RMP 进行求解,得到最优解信息,根据检验数式(11)在候选列中选取列加入到主问题中,然后重复上述过程,直到找不到这种列,说明当前的限制性主问题已经无法改进,即问题最优[16].如果原问题需要得到的解是整数解,则再利用分支定界法进行求解. 首先需要将数学模型转化为依靠列的形式,以方便使用列生成算法进行求解.满足所有约束条件的路径称为可行路径,Ω 为所有路径的集合,为了建立路径与决策变量之间的联系,本文引入以下两个变量: ςir: 路径r经过点i则为1,否则为0; yr: 路径r被选择则为1,否则为0. 由此得到模型的主问题: 其中,目标函数式(12)表示在集合中找到一个子集,使总的飞行路程最短.约束条件式(13)表示选择的路径集合中仅提供每支部队一次支援.约束式(14)表示每个可行路径要么不被选择,要么最多被选择一次.注意到主问题模型中的可行路径集合包含非常多的元素,因此,本文使用列生成算法不断产生对其有改善作用的可行路径加入到主问题中.设子问题中每个可行路径对应的检验数(削减成本)为,如果存在任何的路径满足<0,则将该路径r作为一列加入到主问题中,否则主问题的当前解为最优解. 子问题模型表示为: 其中,σi对应约束式(13)的影子价格,在子问题中为常数,其物理意义表示路径到达网络中每个客户节点的奖励.目标函数式(15)表示在网络中寻求一条路径,使该路径上的总的路径成本减去收益总和最小. 列生成算法子问题又称为定价问题.在本文中,该问题实际上是一种带资源约束的初等最短路径问题[17].本文参考并改进了Desrochers 的标签修正算法[18].该算法的思路为: 在网络中的所有可行路径在其经过的每个节点都带有若干个临时标签,每个标签对应一种资源约束,每次从一条路径上的一个节点的临时标签出发,在其相邻点生成新的临时标签,然后作为出发点的节点的临时标签转化为永久标签,当所有的标签都为永久标签时该算法结束.改进的标签修正算法可以表示为: 步骤1.初始化: 首先得到每个bucket 的长度h=min{tij},∀(i,j) ∈E,然后给初始节点的标签赋值(Tk0,Ck0,Dk0)=(0,0,0),令Pi表示节点的永久标签集合,令Qi表示节点的临时标签集合,令Bp表示第p个bucket.使P0={0,0,0},其他赋值空集. 步骤2.选择bucket: 在所有bucket 中选择第l个bucket,满足如果没有满足条件的l,则算法结束. 步骤3.选择临时标签: 在Bp中依次选择一个标签(Tki,Cki,Dki).如果Bp为空,则转到步骤2. 步骤4.修正标签(Tki,Cki,Dki): 令EEF(Q)表示在标签集合Q中找到所有有效的标签.对于节点i的每个相邻节点j,按条件执行: 转到步骤3. 结合上述建模分析,列生成算法的总体流程图如图2所示. 基于Visual Studio 2012 和Cplex 12.6 平台进行仿真算例的求解与测试,CPLEX 提供了灵活的高性能优化程序,能够解决线性规划、二次方程规划、二次方程约束规划和混合整数规划等多种数学优化问题,并且还在不断地更新改进,是一款功能强大的软件,几乎帮助解决了每个行业中的规划和计划问题,许多先进的软件公司也是CPLEX 的用户.由于没有应用无人机执行作战保障行动的真实案例,本文为了验证列生成算法在求解无人机任务分配问题中的有效性,采用Solomon_25 算例求解VRPTW 经典问题的测试数据. 将各个单位的任务需求按照时间窗序列整理划分,并将运输任务分配模型修正为适合列生成算法求解的集合划分模型,利用该算法对问题进行求解,得到的任务分配路线图如图3. 为了验证算法的性能,本文采用多种智能算法(遗传算法、粒子群算法、差分进化算法等)来求解该问题,多种算法给出的结果都不相同,其中差分进化算法最终解的目标函数最小,即飞行总成本最低,图4给出了采用差分进化算法得到的任务分配路线图.将两种算法求解结果的具体分配方案进行对比分析,如表1所示. 表1 无人机任务分配路线方案对比 图2 列生成算法流程图 图3 无人机任务分配路线图(列生成算法) 图4 无人机任务分配路线图(差分进化算法) 通过标准测试算例的对比结果分析可以看出,两种算法求解得到的路径数量(即需要派出无人机的最大数量)是一致的,都需要但基于列生成算法对任务分配问题进行求解,其算法的精度明显更高,与差分进化算法相比,无人机飞行总路程明显更短,总路线长度缩短了8.84 %,验证了列生成算法在求解大规模运筹优化问题方面的优势. 无人机任务分配优化问题是无人机任务规划系统中的核心技术问题,合适的优化模型和算法能够使无人机实现智能决策、自主高效的完成飞行任务.本文采用的列生成算法是一种基于数学规划的启发式算法,非常适合解决大规模线性问题.通过与常用的人工智能算法进行对比实验,证明了列生成算法具有更高的求解精度,具有更好的应用前景.2.2 构建模型

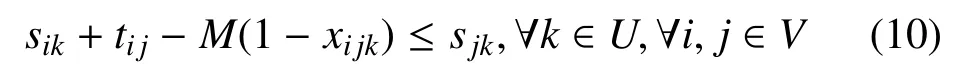
3 模型求解
3.1 列生成算法介绍
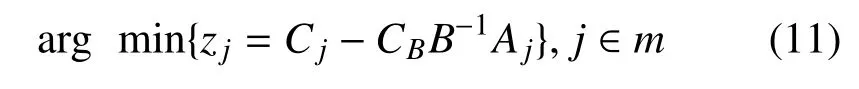
3.2 算法设计
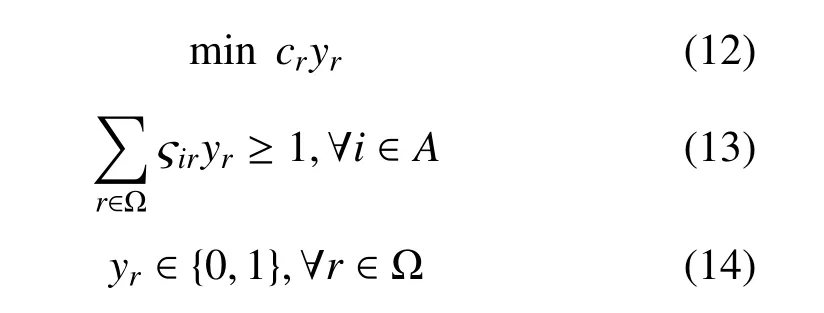
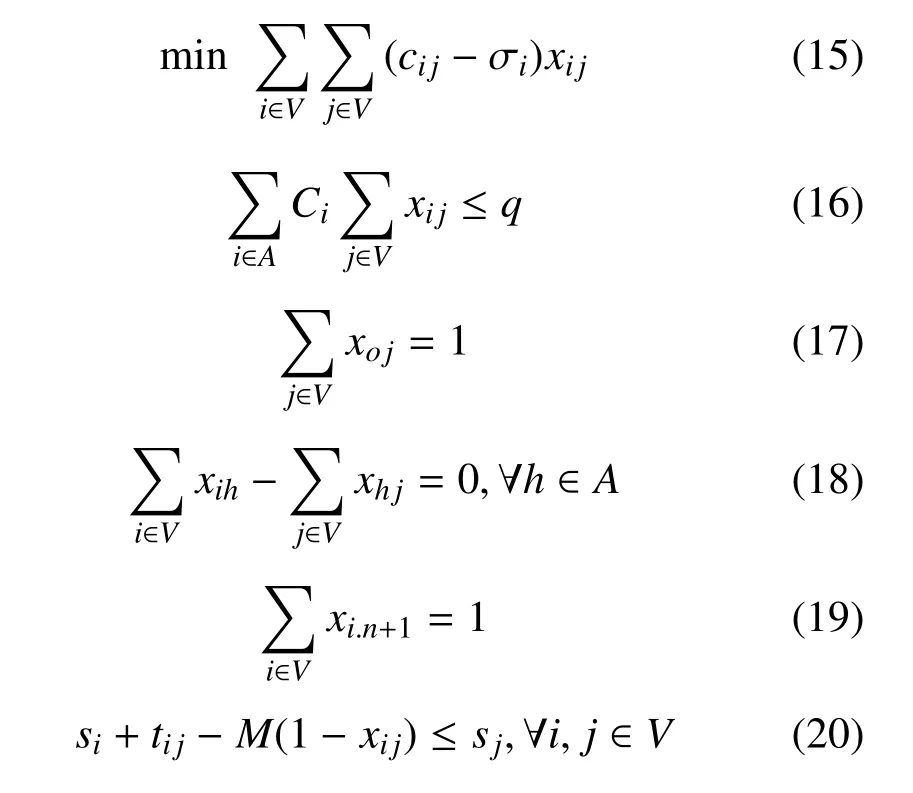
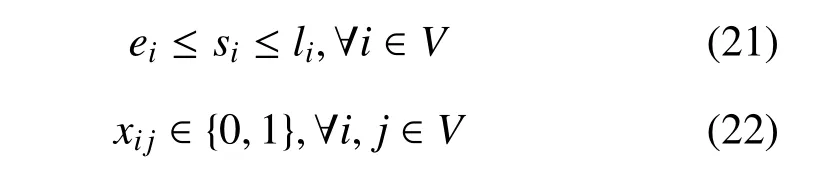
3.3 子问题求解算法
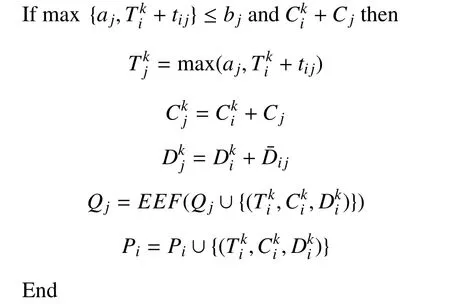
3.4 算法流程图
4 计算实验
5 结论

