近壁声空泡溃灭微射流冲击流固耦合模型及蚀坑反演分析*
叶林征,祝锡晶,王建青
(中北大学机械工程学院,山西 太原 030051)
空化是由于液体环境压力变化而产生的结合非线性动力声学和极端物理学的动态现象,以空泡的反复形成和强烈溃灭为主要特征。19 世纪末,Parsons 和Barnaby 首次提出空化效应,并指出空泡溃灭使螺旋桨叶片使用效率下降。随后,大量学者在空化领域研究并取得了很多突破性进展,对空化效应的研究重点也逐渐由抑制其破坏性转移至利用其破坏性,使空化起到积极作用,如超声清洗、石油钻孔、海洋开发等领域[1]。
依据产生条件,空化主要分为超声空化和水力空化,两者分别通过声压载荷施加和特殊流动系统几何结构改变液体环境压力,进而产生空化现象。水力空化在舰船领域十分常见,诸多学者对水下爆炸气泡运动特性进行了广泛研究。张阿漫等[2-3]运用高阶三维边界元法模拟了水下爆炸气泡的动态特性,自主开发程序系统地研究了近自由面水下爆炸气泡的动态特性。李健等[4]基于VOF 方法对水下爆炸气泡运动进行了数值模拟,研究了距离参数对气泡坍塌、射流及环状气泡的影响。郭娅等[5]考虑了水下近场爆炸冲击波及射流的联合作用,真实地模拟了水下近场爆炸过程。沈壮志等[6]研究了声场中水力空化泡的动力学特性,认为超声将水力空泡运动调制为稳态空化,增强了空化效果。目前,超声空化的研究重点集中在两个方面:空泡动力学理论研究以及超声空化对材料作用的试验研究,前者重点集中在单泡、双泡以及泡群动力学分析[7],后者则重点研究超声空化作用下材料的行为变化及试验分析[8-9],而联系两者间的纽带—空泡溃灭微射流冲击的研究却少有报导。
众所周知,超声空化对材料的作用中,空泡溃灭微射流冲击占主导地位。1944 年,Kornfeld 等[10]首先提出微射流理论,指出当空泡受压力梯度作用或在边壁附近溃灭时,空泡变形为扁平形或元宝形,最后分裂、溃灭,并在溃灭前瞬间,产生一束直径几微米的微型射流冲向壁面。随后,研究者们陆续从理论、试验验证了此观点,并对微射流进行了数学分析。Gregorčič等[11]分别通过高速摄像机观察到了近壁空泡溃灭时产生的冲向壁面的微射流。Plesset 等[12]通过数值计算,指出附壁空泡溃灭时微射流速度约为130 m/s,近壁空泡溃灭时速度约为170 m/s。Dular 等[13]研究了不同温度下的空化腐蚀,结果表明:微射流速度为几百米每秒,且应用微射流方法能很好地预测空蚀趋势。
在微射流对材料具体作用的研究方面,Tzanakis 等[14]认为溃灭微射流是蚀坑形成的主要原因,用干涉显微镜观察了声空化下钢试件表面的点坑,并通过逆向工程及数理统计预测:近壁面声空泡溃灭产生0.4~1 GPa 的冲击压力,且对应的微射流速度为200~700 m/s。Reuter 等[15]通过纳秒激光脉冲诱导产生单空泡和高速摄影记录等手段,研究了近壁单空泡溃灭微射流对受微粒污染玻璃板的清洗作用,对应不同的无量纲空泡壁面距离,提出了三种不同的清洗机理。Soyama 等[16]则利用空泡溃灭产生的冲击作用处理硬铝合金板表面,试验结果表明,材料的疲劳寿命提高超过10 倍。可见,虽然上述空蚀分析、单空泡清洗以及空化表面强化各领域均以空泡溃灭微射流冲击作用为主导,但均未对微射流冲击进行详细理论分析,而此理论分析对于深入揭示超声空化机理、联系空泡理论与作用材料行为以及进一步超声空化工业应用均具有重要意义。
为深入探究声空泡溃灭微射流冲击机理,首先估算空泡溃灭微射流速度,随后依据流体力学、冲击动力学建立率相关的微射流冲击流固耦合三维数学模型,并用耦合欧拉拉格朗日方法分析,探究微射流冲击形成凹坑的几何尺寸及壁面压强的变化,最后通过超声空化试验及反演分析验证理论的可靠性并给出微射流冲击强度、速度的合理预测。
1 微射流冲击流固耦合数学模型
1.1 微射流速度
当传入液体中的超声波声压幅值达到空化阈值时,液体中产生空化效应,在超声波正负压相的交替作用下,液体中的微小泡核历经生长、膨胀、压缩、溃灭等一系列行为。空泡在近固壁面演化时发生不对称溃灭,在溃灭历程早期,空泡远离壁面一侧就产生指向壁面的微射流,空泡由初始的近似球形变为瘦长形再趋近于扁平形,最终微射流突破空泡近壁边侧冲向壁面,造成壁面空蚀损伤。空泡溃灭过程极其复杂且充满随机性,溃灭微射流速度很难精确计算,文献[17]得到了微射流速度估算公式:
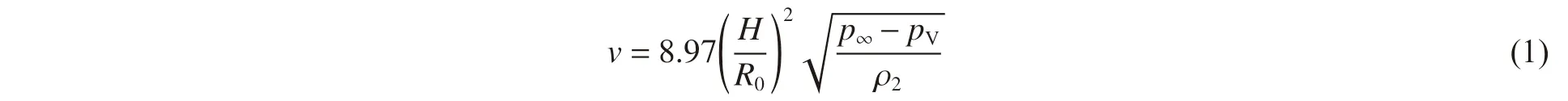
式中:H 为空泡中心距壁面距离,R0为空化泡初始半径,p∞为环境压力,pV为泡内饱和蒸气压,ρ2为液体密度。由于本文液体环境中附加了超声,故p∞=p0+p2sin (ωt),p0为大气压,p2为超声声压幅值,ω 为超声角频率。故针对超声空化这一物理现象,溃灭微射流的速度为:
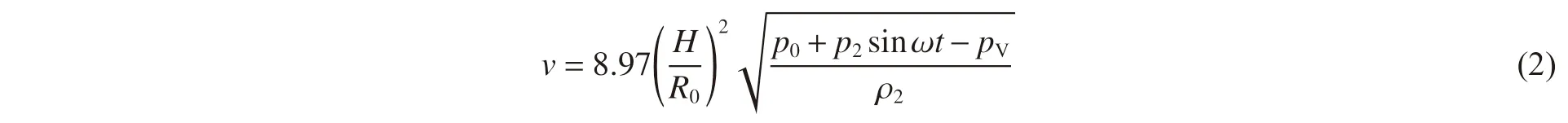
从中可以看出,虽然空泡壁面距离越大,溃灭微射流速度越大,但微射流在冲向壁面过程中速度会衰减,到达壁面时速度反而不高,冲击效果不如空泡壁面距离近时强烈,为便于分析,排除空泡壁面距离的影响,仅考虑H=R0的情况,故在本文具体研究环境中,微射流速度范围为0~479 m/s。
1.2 数学模型
近壁空泡溃灭时产生一束冲向壁面的微射流,会造成材料表面空蚀损伤。微射流以较高速度冲击壁面,在接触壁面一瞬间速度突跃降低,同时产生激波传入液体。激波波阵面后会发生密度、压力突跃变化,称之为受扰动区,此处液体压缩性起主要作用,不可忽略;而波阵面前各物理量基本未变,称之为未受扰动区,此处液体压缩性可忽略。激波离体之后,液体压力降低,侧向射流形成。微射流冲击壁面属于强非线性流固耦合问题,整个过程强烈、复杂且短暂,最有研究意义的是微射流受扰动区的物理行为变化及材料壁面行为变化。首先依据流体力学,建立微射流冲击三维数学模型。
以静止壁面为参考系,微射流以初始速度v0冲击壁面,产生的激波以速度c-v0传入液体,波阵面前后的密度、压力分别为ρ0、p0和ρ、p,微射流冲击示意图见图1。
波阵面后压强突跃增强,通常称为水锤压力,可达到几百甚至上千兆帕,液体的黏性、表面张力及重力与水锤压力相比极小,其影响可忽略,并且微射流冲击强烈且短暂,可忽略外界因素影响。采用欧拉法描述液体行为变化,其控制方程为:
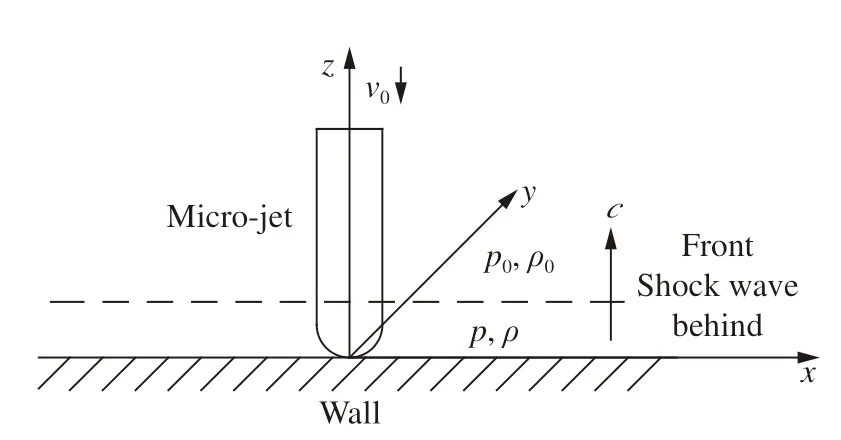
图 1 微射流冲击示意图Fig. 1 Schematic diagram of micro-jet impact

上述两式分别为液体的连续性方程和动量方程,v 为速度向量, ∇为微分算符,且代表散度。上述方程组展开后有4 个方程、5 个未知量,方程组不闭合,需补充液体状态方程,通常情况下液体密度仅是液体压力的函数,如下式所示[18]:

式中:p0、ρ0分别为大气压及大气压下水的密度,B 是常数,可取为3 000,n 为无量纲常数,可取为7。由此,方程组闭合,理论上可得到唯一解,但上述式子本质为流体N-S 方程,得到其一般精确解极其困难,因此,简化上述方程。
以微射流为参考系,看作壁面以速度v0撞击微射流,微射流初始速度、密度及压力为0、ρ0和p0。冲击过程中受扰动区液体的速度、密度和压强可表示为液体初始值与相关摄动值的和,此时物理量均为空间坐标和时间的函数,如下式所示:




式(8)本质为波动方程,冲击较强烈时,声速c 不再是一常数,有[19]:=∇φ,
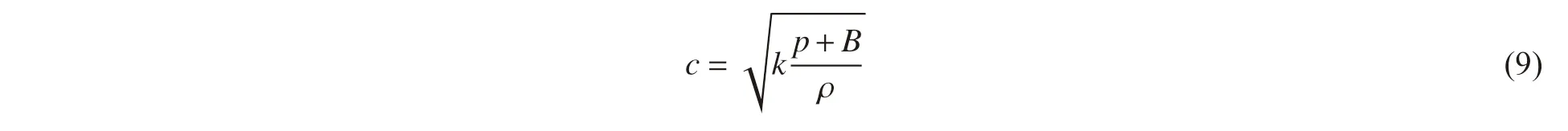
式中:k=7.15。此时式(8)成为非线性偏微分方程。此外,对式(6)中动量方程进行积分计算且引入速度势函数,可得:
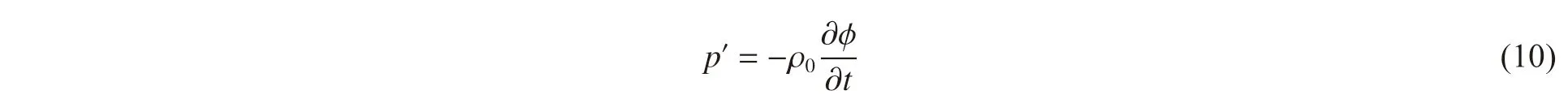
此时,微射流冲击壁面液体区域的物理量已全部得出,控制方程如下:

在固体区域,使用拉格朗日法描述材料行为变化,设壁面质点位移为U(ux, uy, uz),其运动方程为:
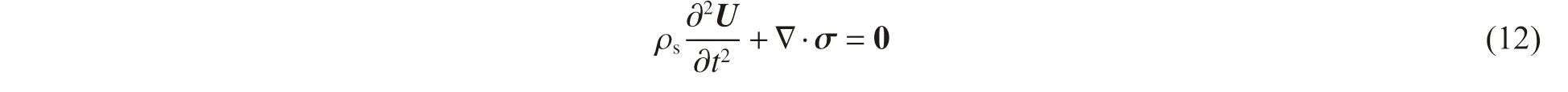
式中:ρs为材料密度,σ 为质点应力张量。由于微射流为短时历高强度冲击载荷,材料变形过程中应变率可高达104~106s-1量级,此时,材料应变率效应不能忽略,故选用典型的率相关本构模型—J-C 模型[20],此模型考虑了材料的应变硬化效应、应变率强化效应及热软化效应,不过本研究中忽略温度影响,则JC 方程可表示为:
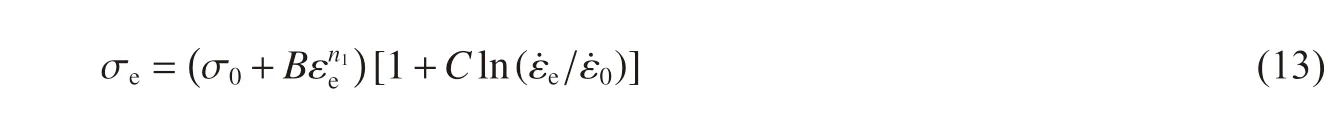
式中:σe、σ0、εe分别为等效应力、屈服强度及等效应变, 为等效应变率, 为参考应变率,B、n1为应变硬化参数,C 为应变率强化参数。本研究壁面材料选用Al 1060,依据文献[21]的有限元模拟结果,可得到Al 1060 的材料参数,见表1。
至此,液固区域的控制方程均已得到,加之初始条件及边界条件,即可得到微射流冲击流固耦合三维数学模型。
液体区域:

表 1 Al 1060 材料参数Table 1 Material parameters of Al1060
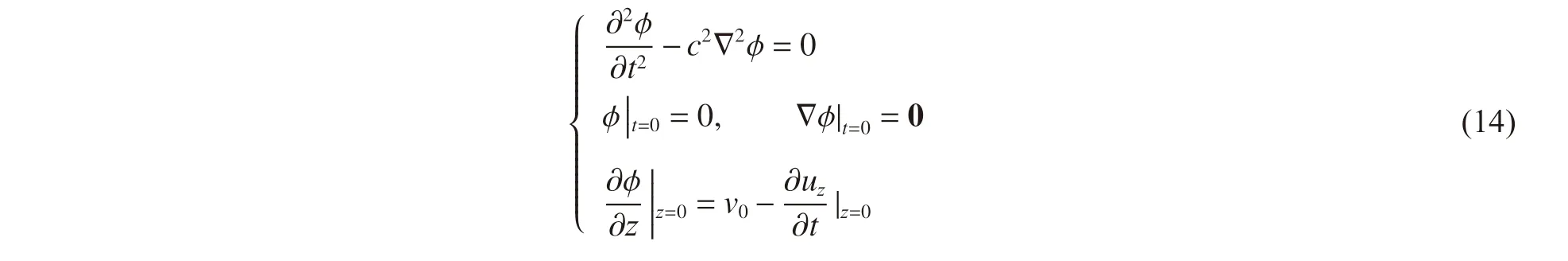
固体区域:
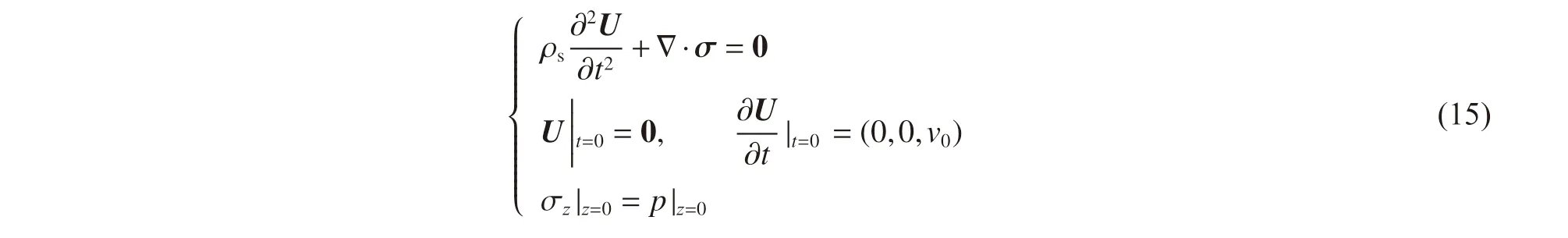
数学模型是一个偏微分方程组,得到其解析解非常困难,故借用有限元模拟的手段对其进行分析,利用耦合欧拉拉格朗日方法模拟分析微射流冲击壁面的流固耦合特性。假设微射流为头部半球形的圆柱,直径为6 μm,初始速度分别为50、100、200、300、400、479 m/s,分析步长为1 ns。
2 结果与讨论
2.1 凹坑几何形貌分析
记微射流半径为r0,r 为壁面上沿x 轴坐标,壁面无量纲距离即为r/r0。微射流冲击下材料发生塑性变形,图2 给出了不同冲击速度下壁面变形深度h 的分布图,结果表明:微射流冲击下材料表面出现凹坑,凹坑两侧有材料塑性隆起,速度越大的微射流冲击形成的凹坑深度越大;相比于凹坑深度,凹坑直径受微射流速度影响较小。为进一步分析凹坑几何形貌与微射流速度的关系,绘制凹坑直径dp、深度hp、径深比dp/hp以及凹坑直径与微射流直径之比dp/dj随微射流速度的变化曲线,如图3 所示。可知随微射流速度增大,凹坑直径和凹坑直径与微射流直径之比虽略有增大但变化不明显,dp/dj处于0.95~1.15,见图3(a)、(d),故凹坑直径与微射流速度无明显相关性。由图3(b)可知:微射流速度小于300 m/s 时,虽然凹坑深度随微射流速度增大而缓慢增大,但其数值很小,形成的凹坑极不明显,故可忽略;当微射流速度大于300 m/s 时,凹坑深度则随微射流速度增大而明显非线性增大,通过比较可知凹坑的直径远大于深度。由图3(c)可见,凹坑径深比与微射流速度有明显的相关性,且凹坑径深比随微射流速度增大而减小,在形成明显凹坑的前提下(即v0≥300 m/s 时),凹坑的径深比处于15~80 之间,这与其他学者的研究结论[22]相符。
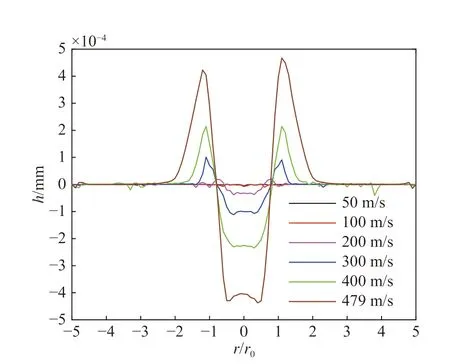
图 2 不同速度壁面变形深度分布曲线Fig. 2 Depth distribution of wall deformation at different velocities
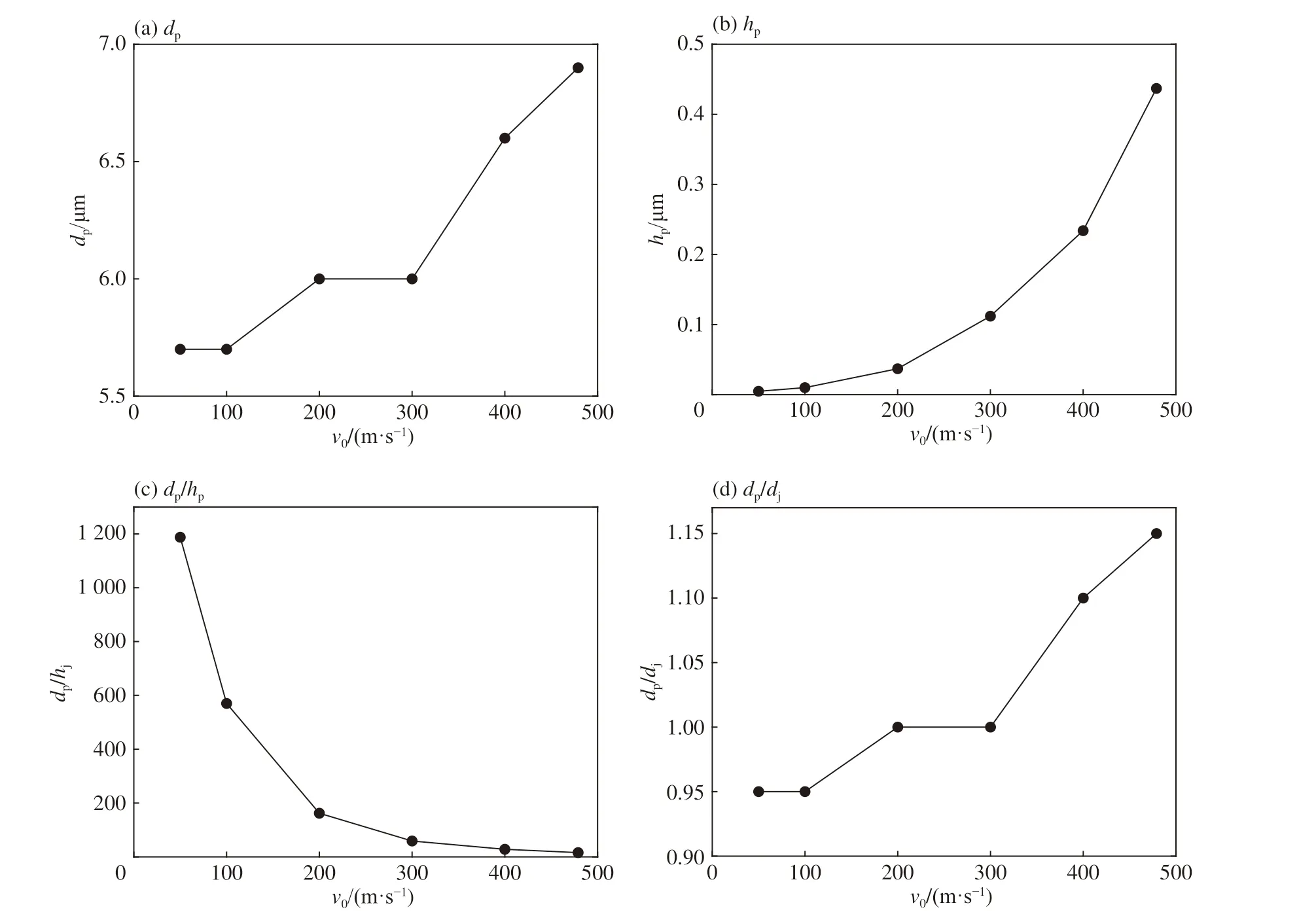
图 3 dp、 hp 、dp/hp、dp/dj 随微射流速度变化曲线Fig. 3 Curves of dp , hp , dp/hp , dp/dj with different velocities
为进一步分析凹坑几何形貌与微射流直径的相关性,定义微射流初始速度为300 m/s,微射流直径分别为4、6、8、10、12 μm,s 为壁面距离,从而进行仿真分析,不同微射流直径下壁面变形深度分布如图4 所示。可见,微射流直径增大,形成的凹坑几何尺寸也相应增大。同样,为对凹坑几何尺寸进行详细分析,提取图4 中数据,绘制凹坑直径dp、深度hp、径深比dp/hp以及凹坑直径与微射流直径之比dp/dj随微射流直径的变化曲线,如图5 所示。随微射流直径增大,凹坑直径近似线性增大,而凹坑直径与微射流直径之比则变化不大,故凹坑直径主要由微射流直径决定,且dp/dj处于0.95~1.2,见图5(a)、(d)。凹坑深度及凹坑径深比随微射流直径增大而略有增加,见图5(b)、(c),但相比于微射流速度,凹坑径深比受微射流直径影响较小。
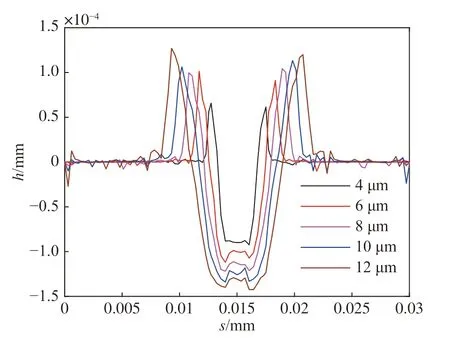
图 4 不同微射流直径壁面变形深度分布曲线Fig. 4 Depth distribution of wall deformation at differentmicro-jet diameters
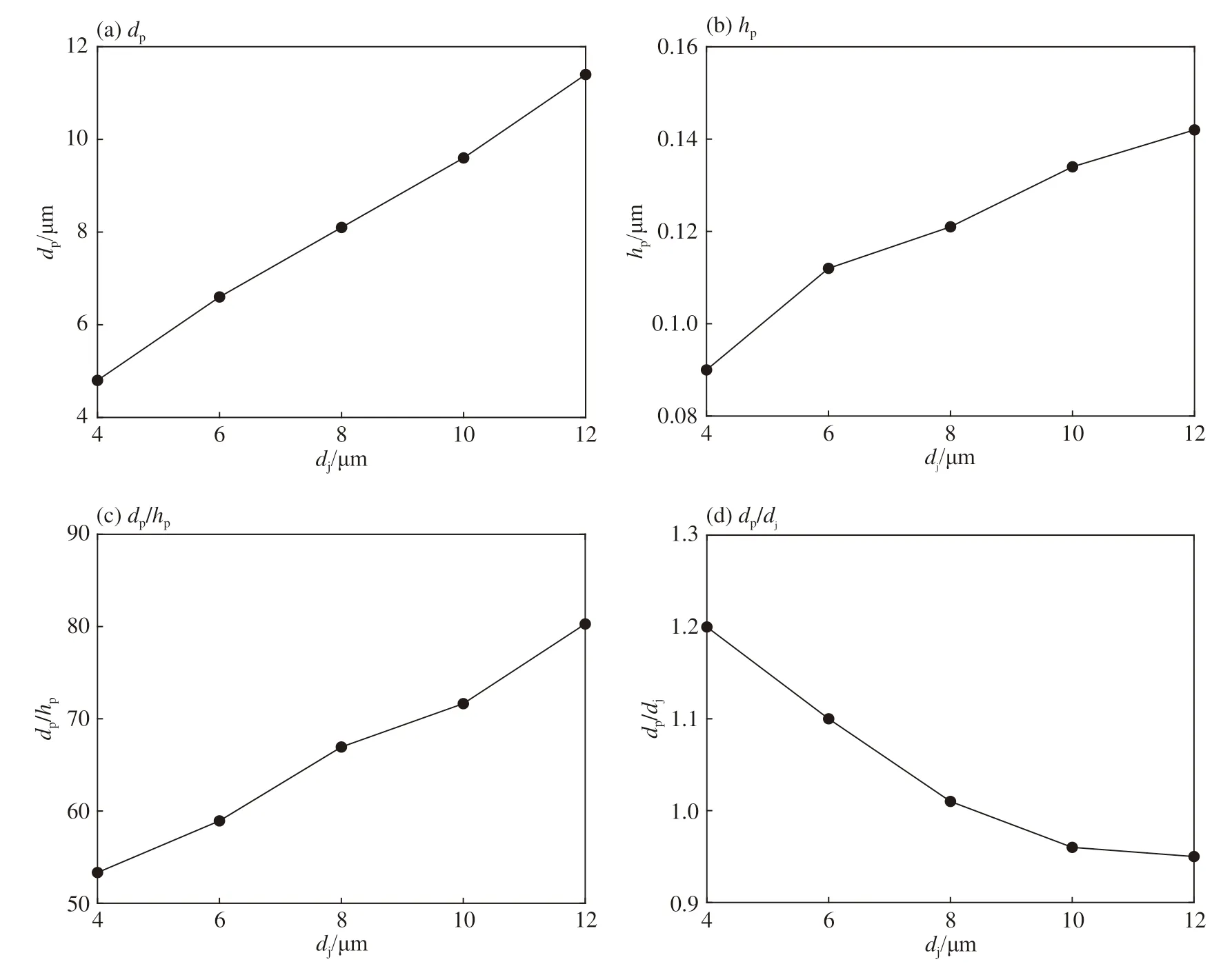
图 5 dp 、hp 、dp/hp 、dp/dj 随微射流直径变化曲线Fig. 5 Curves of dp , hp , dp/hp , dp/dj with different micro-jet diameters
由上可知,凹坑深度由微射流速度及微射流直径共同决定;凹坑径深比主要由微射流冲击速度决定,且冲击形成明显凹坑的径深比约为15~80;而凹坑直径则主要由微射流直径决定,且dp/dj≈0.95~1.2。
2.2 壁面压强分析
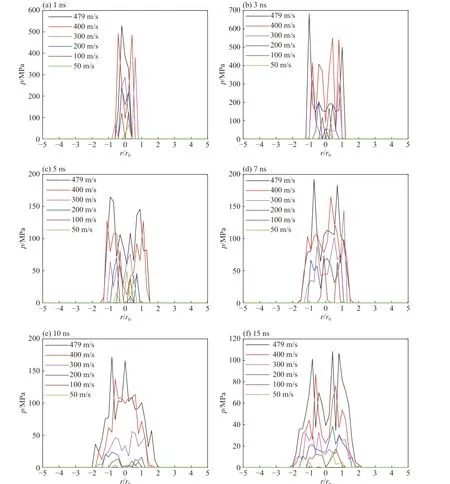
图 6 不同时刻壁面压强分布曲线Fig. 6 Wall pressure distribution at different times
微射流冲击下不同时刻壁面压强分布,如图6 所示。微射流冲击壁面瞬间产生极高压强,并在1~3 ns 内达到最大,见图6(a)、(b),这是由于微射流撞击壁面时速度急剧降低,液体积压以致产生的激波波阵面后液体压缩性不容忽视,从而密度压强突跃增大,随后压力释放,积压液体以侧向射流形式流出,压力降低至一相对稳定状态,如图6(c)、(d)、(e)、(f)。图6 中可明显看出壁面压强随微射流冲击速度增大而增大,壁面压强基本呈对称分布且最大压强出现在微射流冲击边缘,这是由微射流中反向传播的球形激波首先由冲击中心产生并逐渐扩散至两边而导致的。整理不同速度下壁面最大压强,并由式(4)、(9)得到不同微射流速度下液体的最大声速,见图7,结果表明:在冲击速度为479 m/s 时,壁面压强可达682 MPa,此时对应液体中声速即激波速度可达2 435 m/s,这一方面体现了液体压缩性对结果的重要性,另一方面也体现了空泡溃灭微射流冲击的剧烈程度。随后,为验证数学模型及结果的准确性,进行超声空化试验并进行反演分析。
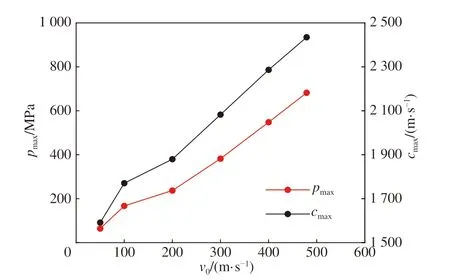
图 7 壁面最大压强及激波速度随微射流速度变化曲线Fig. 7 Maximum wall pressure and shock wave velocityvaried with the increase of micro-jet velocity
3 试验及反演分析
为验证前述理论及结果的准确性,进行超声谐振系统空化试验,并针对材料出现的微小凹坑进行反演分析。为保证试验的稳定性及准确性,试验材料选取厚约1 mm 的1 060 铝薄板。超声谐振系统由超声波发生器、换能器、变幅杆和辐射杆组成,超声波发生器会根据负载变化而自动跟踪频率,从而达到共振。本试验中频率范围为20~20.6 kHz,工具头端面振幅为8 μm,可通过调节振幅百分比控制空化强弱。除超声谐振系统外,主要试验仪器物品有VHX-600ESO 数码显微镜、直径为160 mm 的烧杯、酒精杯、1 060 铝薄板等,放置好超声谐振系统后,将铝薄板固定在钢块上放入烧杯,设置好试验参数后进行试验,图8 为试验示意图。为避免试验后材料表面凹坑重叠,保证单凹坑由单束微射流冲击造成,合理选取试验参数:工具头与材料表面距离3 mm,振幅为8 μm,试验时间为1 min。试验后将薄铝板放入酒精杯中去除残余水分,取出后待铝薄板上酒精完全挥发,将其放置在VHX-600ESO 数码显微镜下观察,试样试验前后表面形貌图如图9 所示,挑选图中有代表性的5 个凹坑并分别记录其直径及深度,见表2。
可见,试验后试样出现近似圆形的微小凹坑,即空蚀坑,其直径大致在4~14 μm,对应深度大致在0.06~0.88 μm,径深比处于16~68,与前述理论结果基本吻合。空蚀坑几何特征符合空泡溃灭微射流冲击结果,可认为空蚀坑主要由微射流冲击导致,这也和空蚀损伤主要由微射流引起的论述相符。由于空化微射流冲击下材料形成的空蚀坑与球形压痕试验中基底材料的变形有很高的相似性,故应用球形压痕试验理论,加之空蚀坑几何特征的测量,可预测空蚀坑应力及空化冲击载荷,进而反演推出空化微射流冲击强
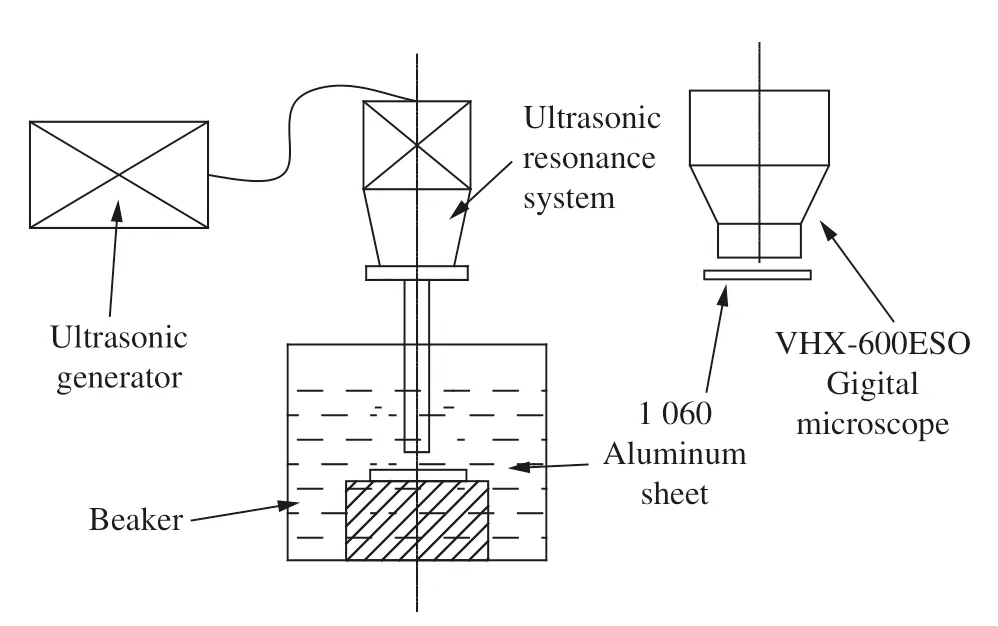
图 8 试验示意图Fig. 8 Test schematic diagram
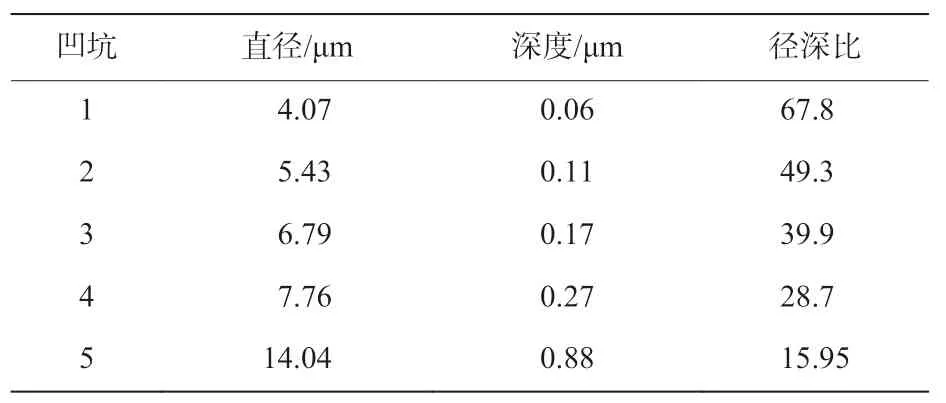
表 2 凹坑几何参数Table 2 Pit geometry parameters

图 9 试验前、后材料表面形貌图Fig. 9 Surface topography of material before and after the test
度及速度。假设单空蚀坑由单束微射流冲击导致空蚀坑为球冠几何形状,且其几何特征可由直径和深度完全描述,依据Tabor 压痕试验的开创性工作,可推导出空蚀坑球冠接触边缘的等效应变εp为[23]:
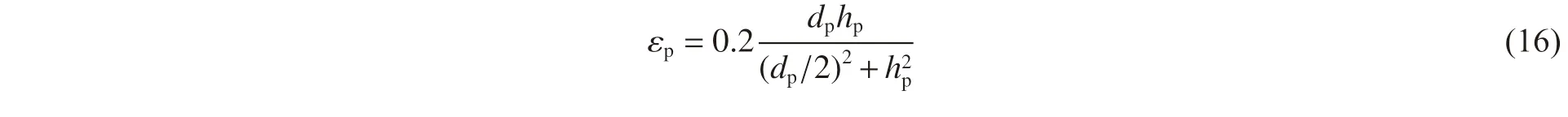
式中:dp和hp分别为空蚀坑的直径和深度。由于本试验中凹坑直径远大于深度,故式(16)可变为:
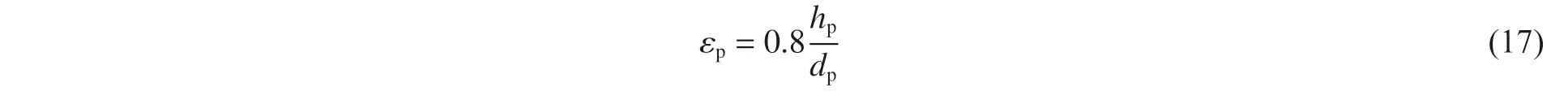
由式(17)可知,空蚀坑等效应变仅与径深比负相关。由前述J-C 方程可得空蚀坑等效应力σp为:
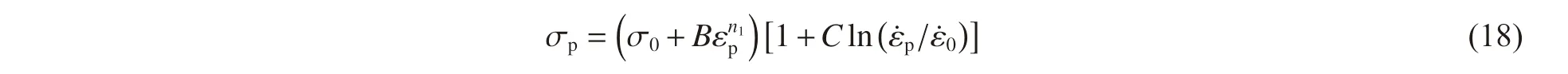
空化冲击载荷Lp为:
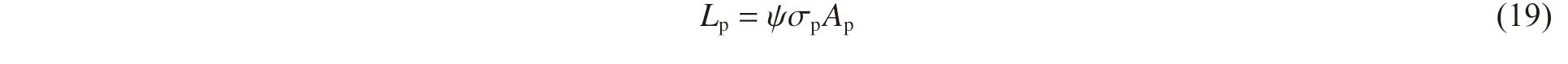
式中:ψ 为Francis[24]提出的约束因子,当材料为完全弹性行为时ψ=1.11,在弹塑性转变过程中逐渐增加且当材料变为完全塑性行为时达到最大值2.87。本研究中,假设空蚀坑发生了完全塑性变形,故约束因子取为2.87,Ap为空蚀坑投影面积,因空蚀坑直径远大于深度,故可写为Ap=πdp2/4。因空化侵蚀主要由微射流冲击导致,假设空蚀坑完全由微射流冲击形成,即空化冲击载荷全部由微射流提供,由前述结论可知凹坑直径主要与微射流直径相关,此处假设dp=dj,则可计算微射流冲击强度σj:
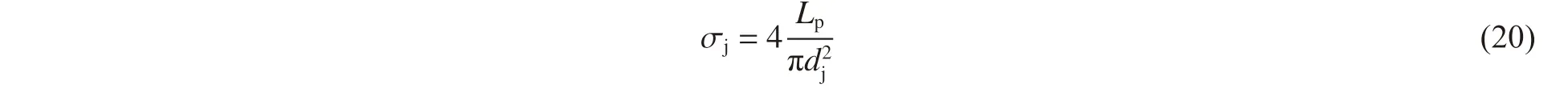
依据水锤方程,即可得到微射流冲击速度vj:
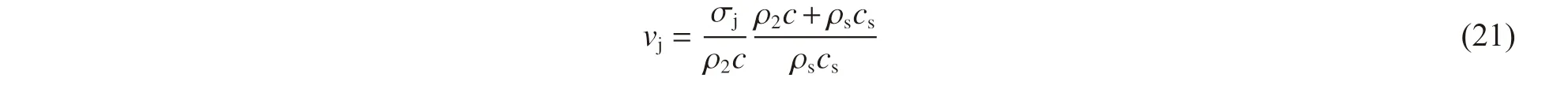
由上述分析可知,等效应变、等效应力、微射流冲击强度及速度均与凹坑径深比密切相关。依据试验结果反演分析,可预测微射流冲击强度及速度随径深比变化曲线,如图10 所示。结果表明:由球形压痕试验理论反演预测的微射流冲击强度及速度与前述理论结果匹配良好,证实了选用率相关J-C 模型的合理性,在16~68 的径深比下,微射流冲击强度为420~500 MPa,对应的微射流速度为310~370 m/s。
本文所得到的空泡溃灭微射流的速度与相关文献的结果相符。一些有关预测空泡溃灭微射流速度的例子在表3 中列出。Grant 等[25]记录了水动力空泡内爆产生的微射流的速度,结果为112~500 m/s。Chen 等[26]分别针对空泡距壁面10 μm 和1 μm 的情况,计算得到了对应产生的微射流速度分别为192 m/s和755 m/s。Tzanakis 等[14]依据逆向工程理论,预测声空泡溃灭产生的微射流的速度为200~700 m/s。Petkovsek 等[27]应用激光诱导产生空泡,并观测到微射流速度可达到780 m/s。此外,针对不同的试验条件,Roberto 等[28]和Futakawa[29]分别提出微射流的速度为200~400 m/s 和250~300 m/s。通过与上述提到的相关文献结果的对比,证实了本文的结果是合理的,选用的方法也是可靠的。
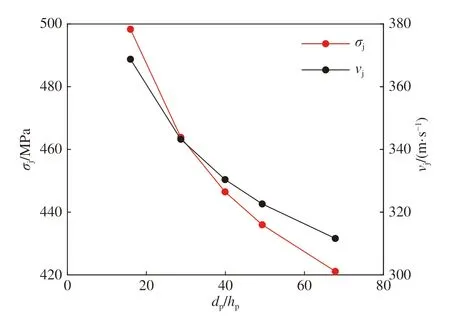
图 10 微射流冲击强度及速度随凹坑径深比变化曲线Fig. 10 Impact pressure and velocity of micro-jet with theincrease of dp/hp

表 3 空泡溃灭微射流速度预测的案例Table 3 Examples of bubble collapse micro-jet velocityprediction
4 结 论
本文利用流体力学及冲击动力学建立了近壁声空泡溃灭微射流冲击的率相关三维流固耦合模型,对其冲击特性进行了分析,并进行了超声空化试验验证及反演分析。结果表明:近壁声空泡溃灭产生的微射流速度最大可达479 m/s;微射流冲击下材料表面会出现微型凹坑,凹坑深度由微射流速度和微射流直径共同决定且随其增大而增大,凹坑直径主要由微射流直径决定且dp/dj≈0.95~1.2,而凹坑径深比则主要由微射流速度决定且其比值为15~80;壁面压强随微射流速度增大而增大,基本呈对称分布且最大压强出现在微射流冲击边缘,压强增大可导致液体中激波速度增大,在冲击速度为479 m/s 时,壁面压强及激波速度最大分别可达682 MPa 及2 435 m/s;超声空化试验验证了微射流冲击下材料表面出现的微小凹坑,基于球形压痕理论的反演分析法表明凹坑等效应变、等效应力、微射流冲击强度及速度均与凹坑径深比密切相关,在16~68 的径深比下,微射流冲击强度为420~500 MPa,对应的微射流速度为310~370 m/s;反演分析结果与理论分析结果相符,验证了选用J-C 材料模型及反演分析方法的合理性及准确性,也为后续工程应用中控制空化强度、微射流速度等提供了理论参考。

