非局部均值滤波在重力异常数据处理中的应用
刘洪波
山东省物化探勘查院,济南 250013
0 引言
重力勘探是以地下介质密度差异为基础的一种物探方法[1],在地质构造、矿产资源和能源勘探等方面应用普遍。重力异常是地下物质密度不均匀分布的综合反映,利用重力异常解决具体地质任务时需对重力异常数据进行处理,以提取出目标地质体异常[2]。低通滤波是重力异常数据处理的常用方法,能够消除重力异常中浅层高频干扰以及非地质体引起的高频干扰,突出异常中的区域特征。位场边界特征是位场数据解释非常重要的信息,传统的低通滤波方法会模糊重力异常的边界,降低异常分辨率。为了克服低通滤波的这一缺陷,杨高印[3]提出了非线性小子域滤波方法,该方法能以较高的分辨率保留异常的边界特征,但小子域滤波存在滤波输出不稳定导致的异常曲线扭曲以及附加高频干扰。马涛等[4]针对小子域滤波法存在子域划分重心不稳的问题,提出对称子域划分方法,使输出结果更加稳定;张凤旭等[5]将小子域滤波应用于重力异常三方向(X方向、Y方向、XY方向),提出三方向小子域滤波,提高了小子域滤波法对断裂平面位置信息的识别;肖锋等[6]对小子域滤波的小子域剖分方式进行了改进,提出‘田’型小子域划分方式,使异常的边界得到加强;蒋甫玉等[7]在‘田’型子域划分方式基础上,加入具有方向信息的四个子域,进一步提高小子域滤波的稳定性并增强小子域滤波对断裂水平位置的识别能力;马国庆等[8,9]提出小子域的‘十’和‘X’型划分方式,并通过水平导数改进小子域判别准则,使小子域滤波输出结果更稳定、合理。
上述对小子域滤波的改进主要集中在小子域的划分方式上,只是针对不同的重力异常数据选择不同的子域划分方式,能在一定程度上提高小子域滤波的稳定性,不可能从根本上改变小子域滤波法导致的重力异常曲线扭曲及高频干扰引入。通过变换子域划分方式改进小子域滤波的稳定性不具有普适性。小子域滤波导致的重力异常曲线扭曲主要表现为高频成分,可通过低通滤波消除这种高频干扰,但是传统低通滤波会模糊异常边界,这与小子域滤波的初衷相悖。非局部均值滤波[10]是一项新的低通滤波技术,能充分利用图像中的冗余信息,在去噪的同时能最大程度地保持图像的细节特征(高频信息)。因此,笔者提出小子域滤波与非局部均值滤波的联合应用,既可增强异常边界又能压制小子域滤波边界扭曲效应,从而提高小子域滤波的稳定性及普适性。
1 基本原理
1.1 小子域滤波
滑动平均可看作是卷积运算过程,在滤波过程中卷积因子(卷积核)不变,取滑动窗口内不同数据的平均值作为窗口中心的输出结果,模糊了异常的边界特征。小子域滤波是对滑动平均法的改进,以滑动窗口中心为中心点划分八个包含中心点的子域(图1),并计算每个子域的均方差;以均方差最小的子域平均值作为整个滑动窗口中心的输出结果。小子域滤波过程的卷积因子是变化的,是一种非线性滤波。
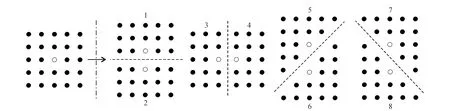
图1 ‘米’型小子域划分方式Fig.1 Division method of “union jack” small sub-domain
以‘米’型子域划分为例说明小子域滤波造成异常曲线扭曲的原因。为清晰地说明问题,假设异常的边界如图2a所示,将图2a离散化,边界两侧的重力异常值分别为1,2(图2b)。图2b中显示了根据小子域滤波原理确定的六个子域,可以看出,小子域在异常边界处很快由低异常区转到高异常区,实现了滑动平均过程对异常边界的保护。但由低异常区到高异常区的快速转变,导致了滤波过程强烈的非线性。
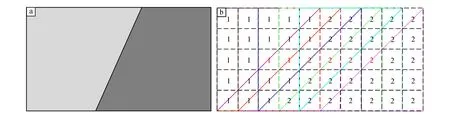
注:图中(红色:1,1,2,2,2,2)表示窗口中心,不同颜色实线三角区域为确定的不同窗口的小子域.a.异常边界模型;b.离散化后数值形式.图2 小子域滤波边界扭曲产生原因分析Fig.2 Cause analysis of abnormal boundary distortion in small sub-domain filtering
图3显示了六个滑动窗口小子域滤波和滑动平均滤波的结果,滑动平均在边界两侧的滤波输出近似线性,因此滤波结果比较稳定,而小子域滤波在边界两侧表现为强烈的非线性,使异常边界弯折,非常小的噪声干扰能引起非常大的滤波误差,导致滤波结果不稳定,造成异常边界的扭曲。特别是当异常边界比较复杂时,非线性放大作用更为明显,不仅造成异常边界扭曲,而且会引入附加高频干扰。

图3 六个窗口中心不同滤波结果Fig.3 Different filtering results in six window-center
不同小子域划分方式及子域确定准则能一定程度上减弱小子域滤波的这种非线性,但是不能从根本上解决小子域滤波输出的不稳定性。虽然小子域滤波输出不稳定是固有缺陷,但是这种不稳定性常表现高频性质。因此,可通过一种既能实现低通滤波又能很好保护高频信息的滤波方法消减小子域滤波造成的异常曲线扭曲。非局部均值滤波能很好地实现这一目的。
1.2 非局部均值滤波
非局部均值滤波[11-14]的基本思想是:计算以当前像素为中心的像素块与邻域内其他像素块之间的高斯加权欧氏距离;以加权欧氏距离与滤波系数为变量构建高斯函数作为图像块间的权值函数,构建此函数的目的是使与当前像素块相同或者相似的像素块获得较大的权重,不相似的像素块则得到较小的权重,通过加权平均这些权值得到当前像素块中心的估计像素值。其具体去噪过程为:
假设含噪图像v={v(i)|i∈I},v(i)表示第i个像素的像素值,其估计值vNL(i)可通过图像内所有像素值的加权平均计算
(1)
式(1)中,w(i,j)为与像素i和像素j相似性相关的加权系数。像素i和像素j的相似性可通过以像素i和j为中心的图像块的高斯加权欧氏距离衡量,即
(2)
式(2)中,Ga表示标准差a的高斯核,Nk表示以像素k为中心的固定大小的图像块。加权系数w(i,j)可由高斯加权欧氏距离计算
(3)
式(3)中,h为滤波参数,Z(i)为归一化常数,其中:
(4)
非局部均值滤波充分考虑了像素i和其他所有像素j的关联性,能最大程度地保留图像的高频细节特征。将非局部均值滤波与小子域滤波相结合既能改善小子域滤波的边界扭曲缺陷又能最大程度地保留小子域滤波优良的边界特征,提高小子域滤波的稳定性与普适性。
2 重力异常数据处理
2.1 模型试算
为了验证非局部均值滤波与小子域滤波相结合的方法可行性和有效性,设计如图4所示的地质模型,包含3个长方地质体,其具体参数如表1所示。

表1 长方体正演参数

图4 模拟的地质模型Fig.4 Simulated geological model
根据表1中的各项参数及图4所示地质模型位置,通过正演模拟获得的地质模型的重力异常如图5a所示。图5b为模拟的重力异常加入小功率的高斯白噪声以仿真实际采集时的高频干扰,同时检验算法稳定性[15]。对模拟的重力异常分别采用传统低通滤波和非局部均值滤波进行处理,处理结果如图5c,5d所示。可以看出,传统低通滤波在压制高频干扰时使异常边界模糊(变宽),而非局部均值滤波在压制干扰的同时能很好地保留异常边界的细节信息,不会使异常边界过渡平滑。
应用非局部均值滤波能在压制小子域滤波产生的高频干扰的同时保留小子域滤波对异常边界压缩的良好特性。图6分别展示了小子域滤波、小子域滤波与传统低通滤波、小子域滤波与非局部均值滤波相结合的滤波效果。图6a表明小子域滤波具有低通滤波的性能,但小子域滤波在压制高频干扰的同时使异常产生扭曲,特别是异常边界部位,使得重力异常等值线不平滑,产生附加高频干扰,对重力异常的解释产生不利影响。图6b为小子域滤波基础上经参数最小的传统低通滤波后的重力异常,传统低通滤波可以消减小子域滤波产生的高频干扰,但是小子域滤波良好的异常边界压缩特性也被破坏,经最小参数的传统低通滤波后,几乎完全模糊了小子域滤波的边界压缩特性,加大传统低通滤波参数,会对边界产生更大的模糊作用。因此,传统低通滤波不适合于消除小子域滤波的固有缺陷。图6c为小子域滤波与非局部均值滤波相结合的滤波结果,非局部均值滤波很好地压制了小子域滤波产生的高频干扰,消除了小子域滤波的边界扭曲缺陷。同时,非局部均值滤波很好地保留了小子域滤波的边界压缩特性。由于非局部均值滤波与异常边界的形态无关,小子域滤波与非局部均值滤波相结合的方法不需要考虑异常边界的形态,具有更强的普适性与稳定性。

a.地质模型产生的重力异常;b.加入小功率高斯白噪声后的重力异常;c.传统低通滤波;d.非局部均值滤波.图5 模拟重力异常及不同滤波方法处理结果Fig.5 Simulated gravity anomaly and different filtering processing results
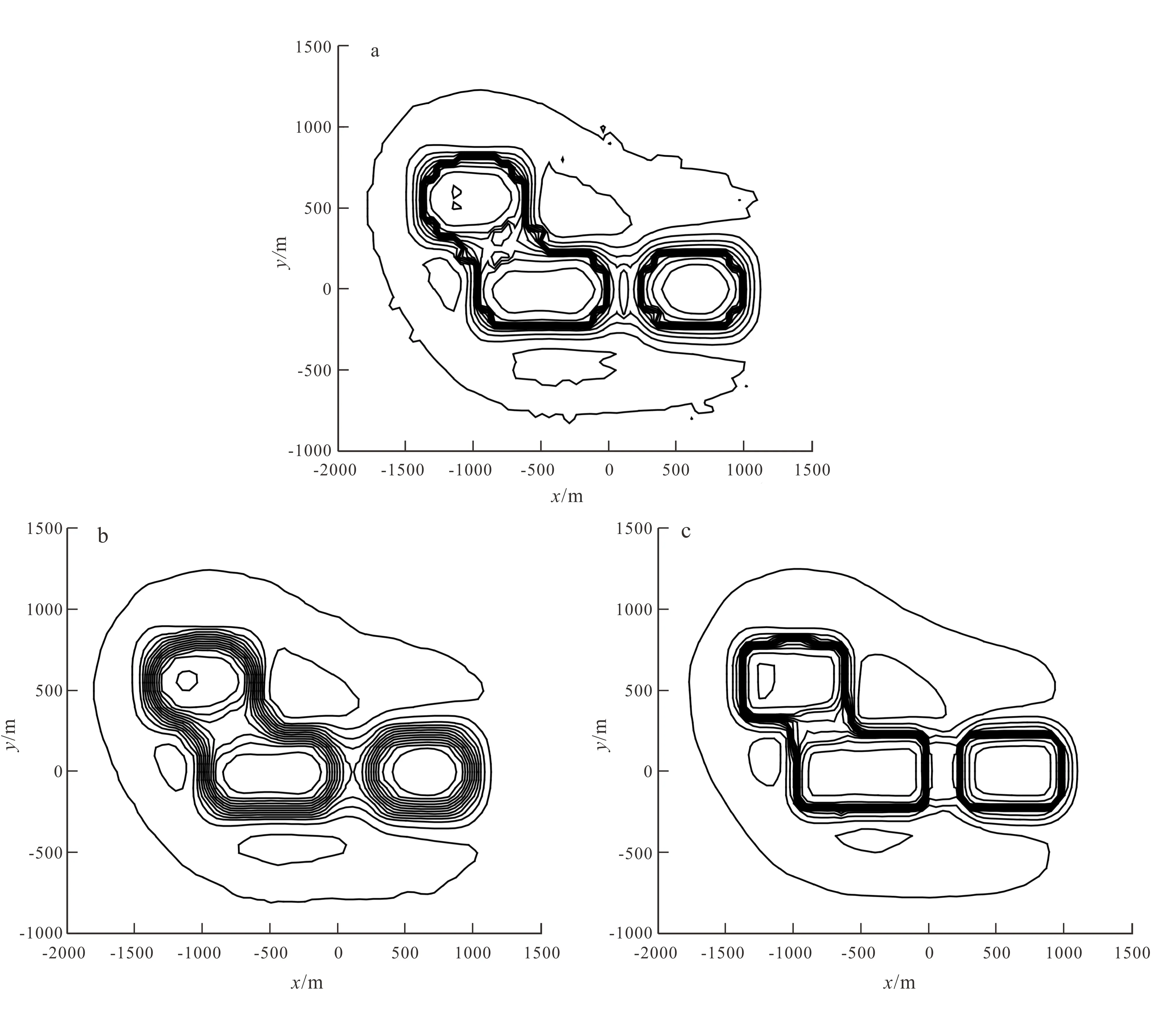
a.小子域滤波;b.小子域滤波与传统低通滤波结合;c.小子域滤波与非局部均值滤波结合.图6 小子域滤波及其联合滤波结果Fig.6 Small sub-domain filtering and joint filtering results
2.2 应用实例
通过莱州湾海域实测重力异常数据处理,分析不同滤波方法的滤波效果,说明小子域滤波与非局部均值滤波相结合的滤波方法对实际数据处理的有效性和优越性。
图7显示了实测重力异常及3种低通滤波结果。小子域滤波增强了异常边界形态,使异常边界更加清晰,但其使异常边界发生扭曲,引入严重的其他高频干扰,降低了重力异常数据的质量(图7b);图7c为滑动窗5×5传统滑动平均滤波,可以看出传统低通滤波能很好地滤除高频干扰,对异常平滑作用明显,但边界形态模糊严重(图7c①、②、③、④),与原始异常数据相比,异常边界等值线变得稀疏,异常分辨率降低;图7d为非局部均值滤波结果,非局部均值滤波能实现传统低通滤波效果,同时能够保护异常边界形态(图7d①、②、③、④),与原始异常数据相比,几乎不改变异常边界形态,能最大程度保护异常边界。

a.原始数据;b.小子域滤波;c.传统低通滤波;d.非局部均值滤波.图7 原始重力异常及不同低通滤波结果Fig.7 Original gravity anomaly and different low-pass filtering results
通过图7分析可知,小子域滤波能够增强异常边界使异常保持很高的分辨率,但小子域滤波会产生严重的异常失真及边界扭曲,而非局部均值滤波能在实现低通滤波的同时很好地保护异常边界信息。图8a、b分别展示了小子域滤波与传统低通滤波和非局部均值滤波相结合的滤波效果,其中传统低通滤波的参数为3×3滑动窗口。图8a中可以看出,即使传统低通滤波采用最小窗口,其对异常边界也有很大的模糊作用,几乎没有保留小子域滤波的良好边界保护特性,但其对边界的保护比直接进行传统滤波要好;图8b可看出,非局部均值滤波与小子域滤波相结合的滤波方法,不但能消除小子域滤波的异常失真,而且能最大程度保留小子域滤波对异常边界增强特性,使得异常的边界相对于直接非局部均值滤波更加清晰。
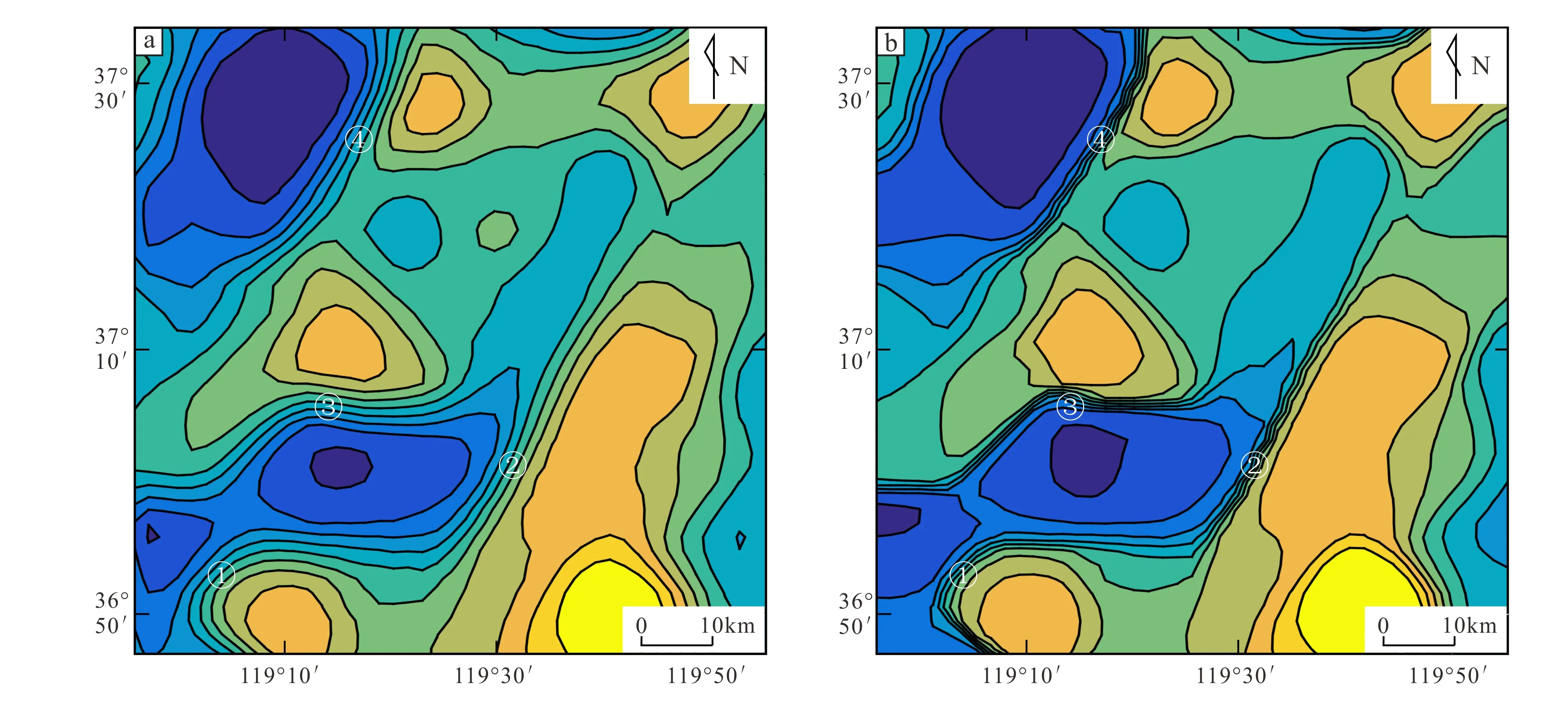
a.小子域滤波与传统低通滤波联合;b.小子域滤波与非局部均值滤波联合.图8 小子域滤波与传统低通滤波、非局部均值滤波联合滤波Fig.8 Combined filtering with small domain filtering and traditional low-pass filtering and non-local mean filtering
当采用较弱非局部滤波参数时,对小子域的附加高频干扰异常压制比较明显,但对小子域滤波引起异常边界扭曲改善不明显(图9)。当采用较强滤波能力的非局部均值滤波参数时,小子域滤波与非局部均值滤波联合滤波对异常边界产生模糊作用。为了能够兼顾高频异常干扰与边界扭曲改善,即使选取较强的滤波参数,仍然能很好地保留小子域滤波的边界增强作用。

图9 小子域滤波与弱参数非局部均值滤波联合Fig.9 Combination of small domain filtering and weak parameter nonlocal mean filtering
3 结论
(1)小子域滤波产生的异常边界扭曲难以通过子域划分方式的改进加以克服,可通过非局部均值滤波加以改善。
(2)小子域滤波与非局部均值滤波联合,既增强了异常边界又压制了小子域滤波边界扭曲效应,从而提高了小子域滤波的稳定性。
(3)小子域滤波与非局部均值滤波联合滤波不需要考虑异常局部形态与子域形态的关系,因而具有更强的普适性,滤波输出更合理,应用效果更好。

