基于双曲Radon变换的混采地震数据重建

王晗，韩立国

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

在常规地震勘探采集过程中,作业周期长,勘探成本较高，随着多源地震混合采集技术概念的提出,勘探成本有效降低。但由于混合震源采集地震数据容易受到地形限制、施工条件、仪器故障等影响，采集的地震数据会出现缺失及不规则的情况。在实际数据处理过程中，数据缺失情况会对后续处理产生不良影响，特别是基于多道处理的算法流程[1-4]。而混采地震数据重建比常规地震数据重建更为复杂，需要对混采数据进行炮分离，对分离的单炮数据进行重建。混采数据在分离和重建的过程中对精度要求较高，这就需要采用高精度分离方法和准确的的重建方法。

在炮分离过程中，在伪分离后的共检波点域使用多级中值滤波法，相比于传统中值滤波法有更高的分离精度，能保留更多的有效信息，为分离后的重建提供条件。但若滤波窗口选择过大，则会丢失一些有效信息，影响滤波结果。国外学者较早对地震混合采集技术进行了研究。Sliverman et al.[5]提出同时激发震源的新思路；Beasley et al.[6-8]使用脉冲型震源进行研究；Bagaini et al.[9]对各种方法进行了横向比较，并将其分类，多源地震混合采集技术(blended acquisition)便是由此成型，国内刘财将多级中值滤波技术应用到地球物理领域[10]，Huo et al.[11]在混采数据的分离工作中使用了中值滤波方法。

针对分离后的缺失地震数据，目前有多种重建方法，基于压缩感知的地震数据重建方法和基于Radon变换重建方法是应用较广泛的方法,其中压缩感知方法中的稀疏变换、迭代算法和阈值模型等的选取将影响最终地震数据重建的效果和计算效率[12]。Radon变换在对分离的单炮数据进行重建后，会进一步消除数据的噪声干扰，基于此，本文采取Radon变换的方法来重建炮分离后的数据。

Hampmson[13]提出抛物Radon变换，Kabiret al.[14]采用抛物Radon变换重建地震数据取得了良好效果。Sacchiet al.[15]尝试用高分辨率Radon变换重建地震道，在牺牲计算效率的情况下提高分辨率。国内王维红等[16]提出采用加权抛物线Radon变换法重建地震数据，一定程度兼顾了重建效率和效果。

在所有的Radon变换方法中，稀疏约束的双曲Radon变换分辨率最高，采用稀疏约束控制改变正则化参数λ，来平衡反演误差与模型稀疏化程度，能够在数据重建中获得更高的精度[17]，符合对混采数据重建精度的追求。然而双曲Radon变换重建地震数据面临的主要问题是双曲Radon变换算子只能在时间域表示，一般用共轭梯度法求解，计算量较大，求解效率低[18-20]。为此，笔者引入了Fista[21]算法来替换共轭梯度法，显著地提高了计算效率。模型试算结果表明，针对混采数据，本文方法在保证计算效率的情况下，取得了很好的重建效果。

1 方法原理

1.1 多级中值滤波的原理

在混采地震数据重建中，第一步进行炮分离，中值滤波作为处理工具，经过多年的发展，此技术已经趋于成熟。中值滤波的原理是设一个滤波长度N(通常为奇数)，以选中的样点为中心取出N个样点，将取出的N个按从小到大顺序依次排列，重排序列中心位置的数值即为输出值。重复此过程即可实现中值滤波[22]。

而二维中值滤波原理为：

(1)

式(1)中，W1(n1,n2)表示以a(n1,n2)为中心的数值序列:{a(n1-N,n2),…,a(n1,n2),…,a(n1+N,n2)}，同理可以得出W2(n1,n2)，W3(n1,n2)，W4(n1,n2)所表示的数值序列。但中值滤波往往存在一些问题，当信号比滤波长度小时，这些较小的细节信号会丢失，导致图像中很多包含重要信息的细节结构受到破坏，这种破坏对数据的影响比噪声本身更为严重。

而多级中值滤波器可以在滤波过程中保护细节信息。其输出定义为:

Ymin(n1,n2)=median[Ymax(n1,n2),Ymin(n1,n2),a(n1,n2)]

(2)

式(2)中，

(3)

(4)

Zi(n1,n2)=median[a(,)∈Wi(n1,n2)],

i=1,2,3,4

(5)

式中，median表示一般中级滤波[23]。

多级中值滤波具有自适应特性，可以保护细节，称之为“自适应程度”，但这种“自适应程度”具有局限性，仅限于Wi(i=1,2,3,4)中选择两个具有极大(极小)中值的基本子窗口，基本子窗口的中值与离散二维信号a共同确定输出Ymin。滤波长度对去噪结果影响较大，降低滤波长度能够保护有效信号，但去噪效果较差；提高滤波长度去噪效果较好，但会破坏有效信息[24]。

1.2 双曲Radon变换原理

混采数据重建的第二步是进行地震道重建，对分离后的单炮数据进行Radon变换，经过Radon正反变换后，缺失的的地震到得到恢复。Radon变换重建原理是基于水平层状介质模型反射波走时方程，走时方程可由级数展开，当模型表现为各向同性时可以用简单的双曲线公式来描述纵波的同相轴，常规双曲Radon[25]正变换为：

(6)

反变换为

(7)

式(7)中，τ是截距时间，p是慢度(速度倒数)，x是炮检距，d(t,x)表示道集数据，m(τ,p)是Radon变换域内数据。在具体实现时，采用离散矩阵代替函数进行程序实现，通常在最小二乘约束下的条件下求取正变换，矩阵形式的Radon反变换公式为:

d=Lm

(8)

式(8)中，d和m表示离散原始数据与Radon域数据的矩阵形式，定义L和LT分别为Radon变换算子和伴随变换算子。建立最小平方意义下的线性化反演误差目标函数，正变换的最小平方解为[26]：

m=[(LTL)-1LTd]

(9)

1.3 稀疏约束反演

时间域内稀疏约束的方法可以提高Radon域内的分辨率，将Radon域数据作为稀疏条件进行约束反演，其中对稀疏约束模型取l1范数，对反演误差取l2范数，变为线性反演问题的l1-l2混合范数求解，建立的目标函数为：

(10)

式(10)中，λ是正则化参数，是平衡模型稀疏化与反演误差的折中参数，λ的值越大，Radon域越稀疏，选取合适的λ值可以提高重建准确度[27]。

1.4 参数选取

在重建时为避免产生假频[28]，需要选择合适的参数，为得到高分辨率的采样结果，给出参数的选取准则，参数的采样率为

Δp=pk-pk-1

(11)

(12)

令Δv=vk-1-vk，得

(13)

当vk和vk-1比较接近时，vk≈vk-1，式(13)变为

(14)

设原始数据中最大有效反射速度为vmax,要使式(14)对所有的有效波场均成立,则式中vk应替换为vmax;同时,当在CSP或CMP道集上做变换时, 选取的范围通常为50～100, 得到临界值关系为：

(15)

1.5 FISTA算法原理

时间域求解Radon变换时往往面临计算量大的问题，其中，时间域算子L和LT是大型的稀疏矩阵，每次迭代都需要计算大型稀疏矩阵L和LT与向量的乘法[26]。求解‖d-Lm‖2时通常采用共轭梯度法，对欠定题给出最小范数解，对超定问题给出最小平方解，因此共轭梯度算法的递推步骤较多，需要求解N*N阶线性方程组，在实际运算中收敛速度也较慢。

快速迭代软阈值算法(FISTA)可以有效地提高计算效率，加快反演的收敛速度，其迭代更新公式为：

m0=[(LTL)-1LTd]

(16a)

x0=m0

(16b)

t0=1

(16c)

当k≥0时：

(17a)

(17b)

(17c)

式中，k是当前迭代次数，soft是取软阈值算子，α是Lipschtiz constant常数，α≥max(eig(LTL))。仅经过数次迭代即可获得高分辨率的Radon变换结果[30]。

2 模型试算及实际资料处理

2.1 理论模型

为检验本文方法的效果，模拟了一个混采模型数据，该地震记录共100道，道间距50 m，每道500个采样点，采样间隔4 ms，具体模型如图1a所示。图1b为模拟该模型缺失地震距数据的情况，使原始数据第40至50道共10道数据缺失，第1道和第20道间隔采样。普通中值滤波法进行炮分离得到图1c，采用多级中值滤波法进行炮分离得到图1d。由图像可见，多级中值滤波很好地完成了炮分离的任务。

对多级中值滤波后分离图1d，使用高分辨率双曲Radon变换进行数据重建，用Fista算法迭代50次，得到高分辨率双曲变换Radon域内结果图2a，其重建后的结果为图2b。比较图1d和图2b可以看出，重建结果十分接近原始数据,并且可以将分离残留部分进一步压制。为进一步验证重建效果，分别对缺失地震道数据图1d和双曲Radon变换重建后数据图2b做谱得到图2c和2d。对比二谱发现，不规则缺失数据出现严重假频，双曲Radon变换重建结果假频明显消除。说明双曲Radon变换有很好的重建效果，能有效地消除假频。

在求解双曲Radon变换时，分别试算了共轭梯度算法和Fista算法，本文的模型测试是在Intel(R)Core(TM)i5-2300 CPU@2.80GHz，16GB DDR3 1333MHz内存的环境下运行。比较两种求解方法发现，在迭代50次的情况下Fista算法耗时123.8 s。而共轭梯度算法迭代150次则耗时324.4 s。可见Fista算法计算效率远高于共轭梯度法。

a.高分辨率双曲变换Radon域内结果； b.高分辨率双曲Radon变换重建结果； c.缺失地震道数据谱； d.双曲Radon变换重建数据谱.图2 Radon变换重建效果对比Fig.2 Contrast of Radon transform results

2.2 实际数据处理

图3a为中国某地区实际地震资料的CMP道集，该数据，每道626个采样点，采样间隔4ms,采样时长2.5 s，共126道，道间距24 m。其中有效反射波的速度范围在1 000～2 000 m/s之间。图3b是对实际数据前30到35道缺失后的数据。对实际数据进行普通中值滤波法炮分离得到图3c，采用多级中值滤波法进行炮分离得到图3d。对比图3c和3d可见，多级中值滤波炮分离效果明显更好。

a.原始数据;b.不规则缺失地震道数据; c.普通滤波炮分离后数据; d.多级中值滤波炮分离后的数据.图3 实际数据炮分离后对比Fig.3 Contrast of separate field blended data

经过双曲Radon变换后Radon域结果如图4a所示，对比重建结果图4b,可以看出实际数据重建效果较好，缺失数据道的位置得到了有效的恢复。实际数据证明了本文方法有较高的实用性。

3 结论

(1)针对混采的地震数据，多级中值滤波与普通滤波法相比，能更好地完成炮分离的任务，确保数据的重建精度。

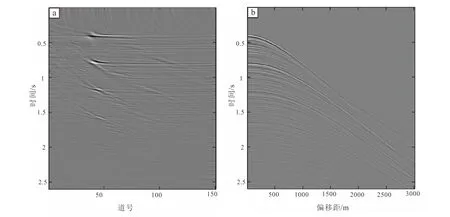
a.双曲Radon正变换后Radon域内结果；b.双曲Radon变换后重建结果.图4 实际数据Radon变换重建结果Fig.4 Radon transform reconstruction results of field data

(2)针对炮分离后的数据，双曲Radon变换可以很好地恢复缺失地震数据，得到准确的地震数据重建结果。

(3)Fista算法在时间域求解的过程中，优化了算法的迭代流程，和常规的共轭梯度法相比，明显提高了计算效率，一定程度上解决了双曲Radon变换计算量大的问题。模型数据和实际数据的重建结果表明，本文方法重建效果好，计算效率高。