基于圆筒形电容器的粮食含水率测定研究

李靖轩 冷文秀

(中国石油大学(北京) 1石油工程学院； 2理学院，北京 102200)

水分是粮食的重要成分，在维持细胞的呼吸作用、储存等方面有重要作用。20世纪八九十年代，国内研究粮食含水率测定主要采用传统烘箱干燥法，但由于耗时费电，局限性较大，后被逐渐淘汰。近年来，有很多学者利用介质的电特性对粮食的含水率进行测量,目前比较常用的有附加电阻法、屏蔽电感法、同轴线相位法、电容法等手段。由于较平行板电容器而言同轴圆柱形电容器精度高、容量大，能有效减小边缘效应[1]，本文拟采用同轴圆柱形电容器测量粮食含水率。

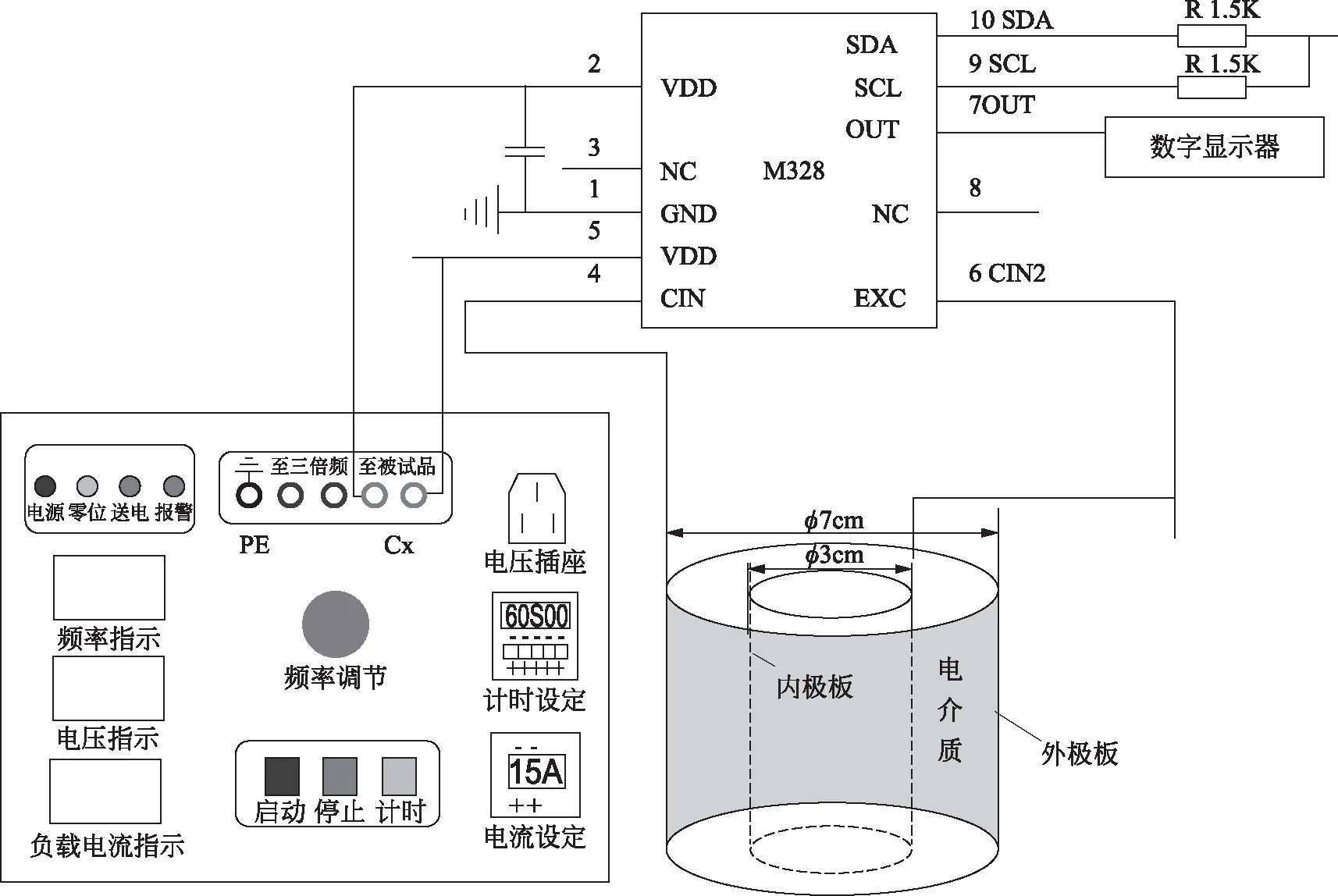
图1 测量电路整体设计

粮食作物在一定程度上属于电介质[2]，本文以粮食作物作为电容器的极板间介质，保持电容器的正对面积、极板间距离等因素不变，通过测量电容值、装载密度和被测粮食的含水率，并进行单一因素正交化分析，后用Matlab软件进行拟合，最终得到含水率-装载密度-电容的函数关系式。此实验有助于开发粮食含水率快速检测仪器。

1 测量装置的构造与原理

1.1 电容器装置构造

含水率测量部分用铜质圆柱形同轴套筒作为电容器两极板，与平板式电容器相比，圆筒形电容器受边缘效应作用小，实验步骤也更加简单。圆柱型电容器由两个不同直径的黄铜制圆柱形套筒组成，套筒的一端用塑料底板固定，并使二者在同一轴线上，每个套筒外壁用焊锡焊接一根导线，以供接入电路时使用。两套筒高为L(10cm)，外电极内径D为7cm，内电极内径d为3cm，管壁厚0.2mm，当满足条件L≥(D-d)时，可忽略圆柱的边缘效应。

1.2 单片机原理及编程

电容测量主体部分采用Atmega328单片机，属于AVR系统单片机，它是增强型内置Flash的精简指令集CPU高速8位单片机，可广泛用于计算机外部设备、仪器仪表、通信设备等各个领域[3]。M328单片机内嵌有Flash程序存储器，擦写方便，本次实验采用IAP语言指令。与M128不同，M328单片机是8位低功耗CMOS微处理器，提高了芯片的集成度和器件的速度，降低了电压和功耗。内部采用大容量快闪存储器，实现在系统中烧录程序(ISP)和在应用中烧录程序(IAP)的技术。M328单片机具有32个通用工作寄存器，这种结构能在很大程度上提高代码效率[4]。虚拟Flash数据载入和读出寄存器的逻辑框图如图2所示。数据输出部分采用LCD12864图形显示。使用IC锁紧座，方便元件直插，贴片座最大能支持TO-252封装的元件。LCD显示器可在低电压(3～6V)，低功耗(0.3～100mW)的条件下工作，可适应实验测量电路的强度要求，并且可与之前的CMOS信号调理电路直接匹配[5]。

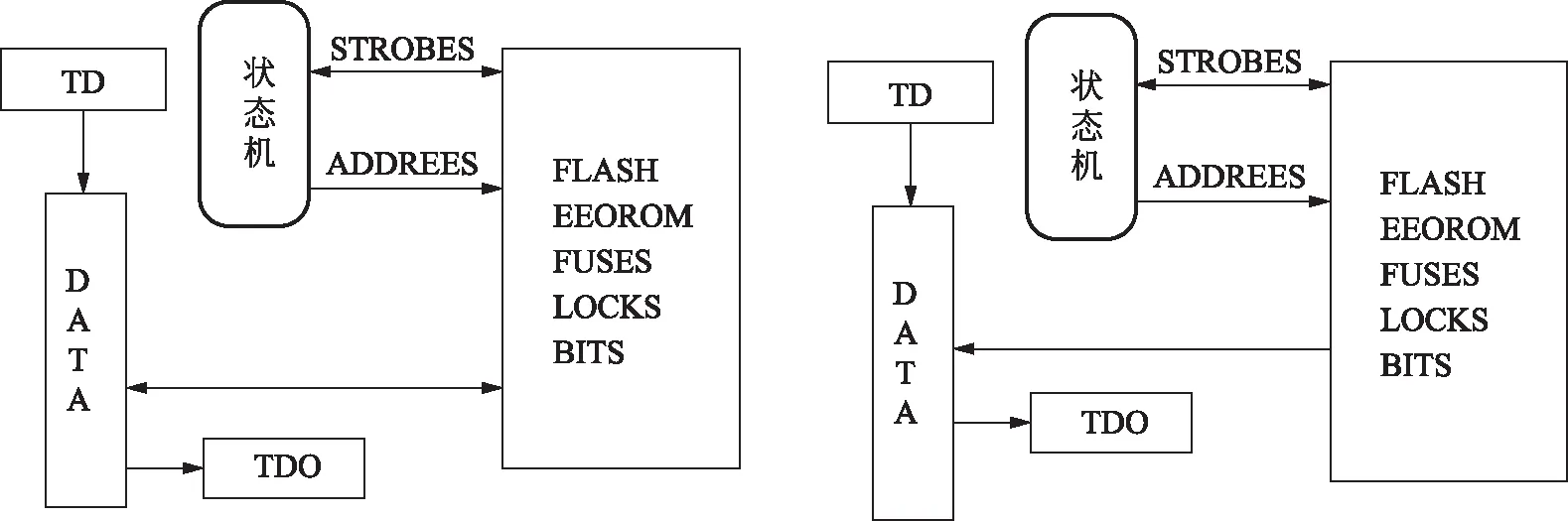
图2 Flash数据载入读出逻辑框图

2 实验步骤操作方法

2.1 合理测量频率的确定

由于以大米为介质的电容器的电容值很小，大概只有30～50PF，所以一般的测量电路如电桥测量法、运算电路法等误差比较大，电路很容易失稳。由于实验所用电容传感器的电容较小，要求设计的检测电路具有检测微小电容变化的能力。杂散电容是影响微小电容检测的关键，为此本实验采用能抗分散、杂散电容的交流充放电式电路检测微小电容[6]。

实验时需要通过改变频率，测量相同含水率的粮食，找到电容变化最为明显的曲线，得到在测量实验中能显著地反映大米含水率变化的测试频率。实际测量过程中频率的范围是100Hz～1MHz，电压为9V，粮食的含水率为5.5%～49%，根据实验数据得出关系图3，从100Hz到1MHz范围内以大米为电介质的电容器均可测得其电容，高频条件下要比低频条件下含水率测量范围大，但电容变化不明显，综合考量测量范围和敏感程度，发现在10kHz测试频率下，含水率可测范围约为10%～35%，可满足一般测试需要，并且在此范围内，测试点连续性好，电容变化明显，增长率较大，故选择测试频率为10kHz。

由于测试频率不高，加上传感器的电容值很小，可忽略在高频环境下易出现的一些寄生参数，包括等效串联电阻(ESR)和等效串联电感(ESL)，二者都是由电容器的引脚与电容器两个极板的等效电力参数串联造成的，在高频环境中尤为突出[7]。

2.2 合理测量温度的确定

此部分实验主要探究粮食含水率恒定条件下，不同温度对应传感器电容的变化规律。温度的测定采用温度计。大米在特定含水率条件下，改变其温度会引起电容变化。根据实验数据可看出虽然此测量体系对温度的变化灵敏度不高，但随着温度的升高测定的电容值也确实随之增大，所以温度对于实验的影响不可忽略。从测量数据可以得出，如果以水在30℃时的介电常数为基准点，则在全温度范围(20～75℃)内，大米的介电常数相对变化率为-70%～190%，所以测得的电容值要考虑所处的环境温度情况。实验时每次测量电容前需测量温度，使之保持在一定范围内。

用Matlab中的polyfit功能求得拟合方程后再求导，找到电容变化率最大时的温度，为24℃，此时，电容值增长率最大，传感器最为敏感。

通过该变换，可以将瞬变电磁场分量随时间t的衰减曲线转换为波场随类时间q的传播曲线，所以可以利用地震数据处理方法来求解转换波场的物性与几何参数。利用变步长的梯形公式：将式(1)的积分方程离散化，并写成矩阵形式为

2.3 电容影响因素的单一分析实验

被测大米的含水率、密度、环境温度等是电容数值的主要影响因数。为了确定各因素所占比重，需要进行单一变量的对比实验并得到电容-含水率-粮食密度数据，最终通过单因素正交分析得到拟合度较高的函数关系式，并且能够通过所测得的电容值及粮食密度求得大米的含水率。

图3 不同频率下电容—含水率图

选取普通市售大米并充分日晒干燥。实验对大米含水量的标定采用了105℃恒重法。烘干至前后两次重量差不超过0.005g，此时可认为大米含水率为零，拟定此时的质量为标准质量，记为m0。将大米在室温下用温水浸泡一段时间后捞出散开放置在吸水纸上，在室温下自然晾晒(表面水分含量过高会影响数据准确度，可用吹风机缓慢吹干表面水分)，可由自然晾晒时间长短来控制大米含水率的变化，将含水大米质量记为mi，其含水率大小为

(1)

另外，大米装入电容器时由于自然沉降作用会产生填充密度不均，装载方法不同会造成疏松程度不同，这些因素都会对实验数据的精确度造成影响。为了解决这个问题在填充时用晾晒后的大米(干燥大米的载装密度约为0.8 g/cm3)与质量不等的PVC粉末充分混合，由于PVC粉末粒径较小(微米级)，能够很好地填充在米粒间的孔隙中起到支撑作用，解决填充密度不均、疏松程度无法精确控制等弊端。为了找到PVC粉末的适当混合量，实验时逐渐增加PVC粉末质量，减小混合物中大米的载装密度。

在计算时，利用公式2可计算混合介质中大米的载装密度：

ρ=mi/V

(2)

其中V为圆筒形电容器的环空体积。由于电介质为混合物，且两种物质介电常数相差不大，不能忽略PVC粉末部分对于电容测量的影响，所以在测量时需利用混合物介电常数立方根相加率和圆筒形电容器电容计算公式联立求得混合介质中大米部分所占电容Ci为

(3)

式中，ε为混合物的介电常数；εi为第i种成分的介电常数；ni为混合物中第i种成分的体积与总体积V的比值；C为混合介质的电容，即电容测量装置的示数，利用公式(3)即可求得混合介质中大米部分所占电容Ci，最终得到所测量大米的载装密度、含水率、电容的实验数据见表1。

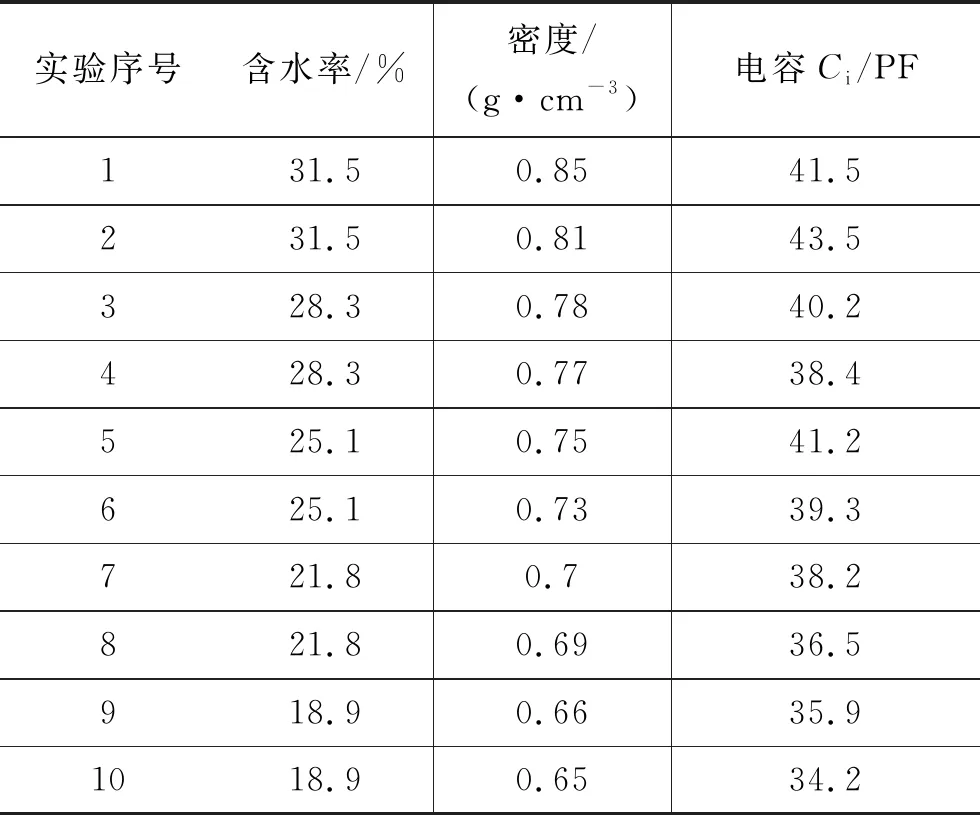
表1 含水率-载装密度-电容测量数据

上述实验完毕后还需测量在含水率W0不变条件下的ρ-C数据，试验时所用大米含水率为25.3%，因为此时电容值较大，由于测量造成的相对误差较小。为保持含水率不变，实验时一次性将相同含水率的粮食均分成多份，之后分别装进塑料袋进行密封，每次实验只需用一份塑料袋中的粮食与不等的PVC粉末混合即可，并等待测量数据稳定后读数，得到电容-载装密度关系曲线如图4所示。

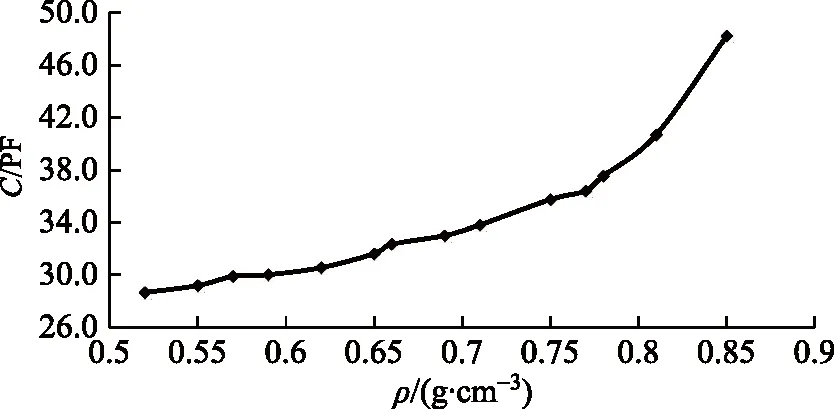
图4 含水率25.3%时电容-载装密度关系图

3 实验数据分析

3.1 求解回归方程

由图4中曲线和数据可以看出，随着大米载装密度的增加，其对应的电容值也随之增大，但不是线性关系，需要做进一步分析。

图5 逐步回归分析图

设y为电容值C(PF)，x1为含水率W0(%)，x2为载装密度ρ(g·cm-3)，y是x1，x2的高次组合函数，即

(4)

之后用Matlab软件中的cftool工具箱进行阶数的判断，并用polyfit模块试求x的最高次，可得到x的最高次为2，所得到的逐步回归分析如图5。图中，条形图旁的数据表列出了所有未知项的回归系数值，以及统计量和有关的显著性概率。

根据回归分析图可知第五个变量不在模型之中，故剔除第五个变量x1x2，回归方程的相关系数R2=0.983，均方差RMSE=0.747，回归的总F统计量为232.334，显著性概率P=5.969e-14<0.05，说明方程在5%的置信水平上显著，根据残差分析图继续求得方程的常数项为a0=23.2852，故回归方程为

(5)

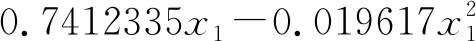
3.2 单因素数据实验方程验证

虽然已经得出C-W0-ρ的函数关系式且置信水平较高，但我们无从得知关系式的正确性，故要进行方程验证，选取含水率为25.3%时的数据(即图4中的数据)进行验证。实验数据和变异后数据见表2。

表2 载装密度的单因素实验数据

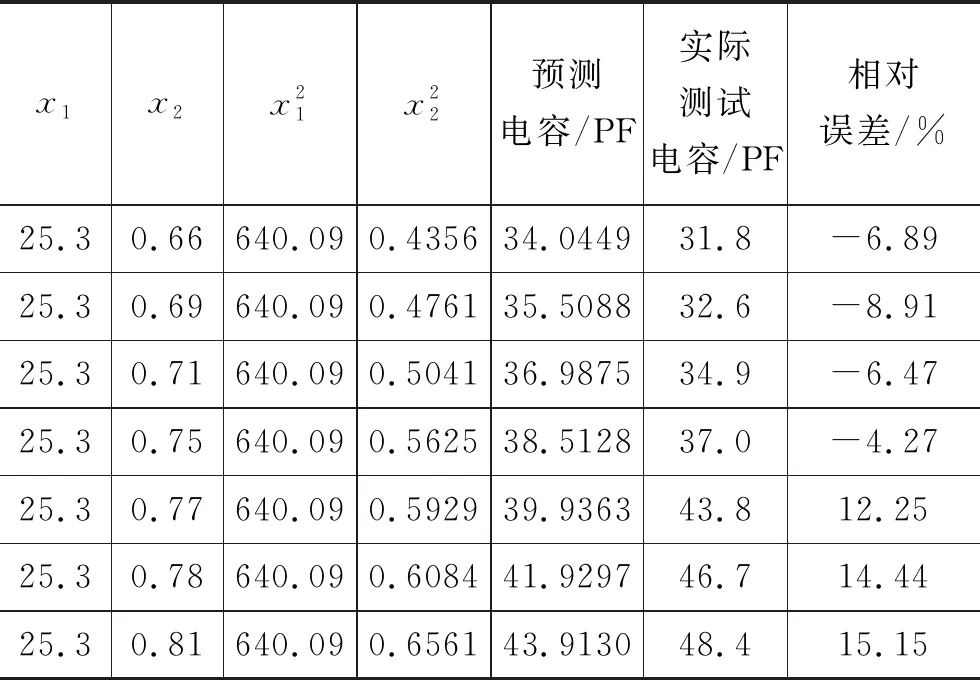
续表

从表2数据可以看出当载装密度超过0.77g·cm-3(PVC粉末含量很少)时，相对误差会超过10%，当装载密度小于0.77g·cm-3，平均相对误差的绝对值为6.33%<10%，说明本实验通过将PVC粉末与大米混合有效地解决了只填充大米时造成的填充密度不均、疏松程度无法精确控制等弊端。

实验结果表明对于单个因素的实验数据而言回归方程的预测值与实际测量值有一定差距，经分析不难得知单片机系统与电容传感器存在接触电阻，与理想模型存在差距。或是由于传感器表面一直与被测粮食紧密接触，并未进行干燥或清洁，这样也会在传感器表面积累水分，影响测量结果。当装载密度小于0.77g·cm-3，平均相对误差的绝对值为6.33%<10%，说明所建立模型与实际具有较高的拟合程度，能满足一般的测量精度要求。

4 结论

(1) 本文设计了一种同轴圆筒式粮食水分测定仪器，其核心构件为圆筒形电容器和M328单片机。由于以大米为介质的电容器电容较小(PF)，为了避免引入杂散电容而影响测量精度，电容器部分采用边界效应较小的圆筒形电容器。检测硬件部分采用M328单片机，将电容通过信号调理转化成电信号，从而实现对微小电容的测量。该仪器能有效地减小引入误差，精度高且重复率好。

(2) 研究了温度24℃，在大米含水率19%～32%、容积密度 0.65～0.85g·cm-3范围内，电容值与含水率、装载密度的关系，建立了含水率、装载密度和电容值的二元二次方程并对回归模型的准确性进行了验证，结果表明该水分仪测量的水分值与实际水分值的相对误差在7%范围内，说明所得关系式具有较好的适用性。

值得一提的是，对单个因素试验数据而言，虽然整体的逐步回归方程的预测值与实测电容值相对误差较小，但不满足规范的二次曲线，通过曲线也能看出电容值有局部的增益，这需要我们继续分析，查找原因，由于时间和条件限制不做过多讨论。