从认知语义学的视角看数学方法在物理学中的应用

贾光一 刘玉环 张靖雯 龚 洁 霍亦琦

(天津商业大学理学院，天津 300134)

大学所学的数学方法不只是一种工具，还应该是对自然规律、物理现象的归纳与概括，更应该是一种对科学思维的训练。但是对于物理教师来说，将数学方法融入物理教学中并不是一件容易的事。要想实现数学方法助益于物理教学的目的，需要搞清楚物理学中的数学与纯数学的不同、学生学习数学和物理的认知过程，需要在教学过程中帮助学生学会数学方法在物理学中的意义建构，从而将数学方法合理地融入而非简单地加入进物理教学中。

1 物理学中的数学不同于纯数学

案例1： 调查对象：大学一年级第二学期数学和物理学专业本科生；调查方式：问卷调查。

问题： 请根据函数E(x,y,z)=1/(4πε0)·Q/(x2+y2+z2)给出E(r,θ,φ)的表达式。

我们发现，物理学专业的很多学生会直接给出E=1/(4πε0)·Q/r2(A同学)；对于数学专业的学生，有人会给出E=1/(4πε0)·Q/[(rsinθcosφ)2+ (rsinθsinφ)2+(rcosθ)2]=1/(4πε0)·Q/r2(B同学)，也有同学会给出E=1/(4πε0)·Q/(r2+θ2+φ2)(C同学)。尽管A同学和B同学得到的最终结果是一样的，但经过询问得知，A同学认为，题目中的公式可以理解为位于坐标原点位置处点电荷Q在空间某位置电场强度E的计算公式，E只与距离r有关。

该案例说明，物理学专业的学生在解决问题时通常赋予数学符号于物理意义，看到公式后认为E和Q分别表示电场强度和电荷量，所以会直接给出E和r的物理关系；数学专业的B同学在解决问题时采用的是逻辑推断，想到的是直角坐标系与球坐标系之间的对应关系，通过坐标变换得到E和r的数学关系；数学专业的C同学认为x,y,z以及r,θ,φ均为虚拟变量，是互相独立的、不具有任何物理意义的数学变量，所以会在函数关系中直接进行数学符号的替换。

除了对数学字母或符号的认识不同，数学和物理在正负号的分析上也会大不一样。在实数范围内，数学中一般认为正数大于负数，但是在不同的物理问题中正负号有着不同的物理意义，而不是用来表示数值大小，例如，力、位移、电场强度等物理矢量，其正负号的变化仅意味着它们的方向与事先选定的坐标轴正方向相同或相反；在热量前面加正负号是为了区分一个热力学系统从外界吸收热量还是向外界释放热量；在法拉第电磁感应定律ε=-dΦ/dt中，负号表示感应电动势ε总是与磁通量Φ变化的方向相反等。

此外，数学学习者与物理学习者还会对函数的概念及其表示方式存在差异。比如，在数学中z=xy说明y与x成反比，y与z成正比；然而在物理学中F=qE的函数关系中，电场强度E是由电场本身的性质所决定的，与试探电荷q无关，所以不能认为E与q成反比、E与F成正比；又比如弹簧的弹力F和弹簧的形变量x成正比，即F=-kx，但k是弹簧的劲度系数，只由材料的性质所决定，不与x成反比；类似的还有物质的吸热量Q与比热容c之间的函数关系Q=cmΔT、导体两端的电压U与电阻R之间的关系U=IR，c与R均由物质本身的性质所决定，与其他变量无关。如果我们在等号左侧加上括号和自变量，比如Q(m,ΔT)=cmΔT，那么数学学习者也会认识到c与其他变量无关，但在物理表述中，我们并不需要这么麻烦。

这些简单的实例说明，数学方法在物理学的运用中通常被赋予了特定的物理意义，从而助益于物理的表述与计算。但这并不意味着物理学习者就一定能看到数学符号所隐含的物理意义，如上文提到的部分物理学专业的学生不清楚行列式与矩阵在物理学中有何应用。

2 数学方法在物理学中的意义建构

意义建构是学习过程的最终目标[3]。数学方法在物理学中的意义建构就是要帮助学生对所学习的数学方法与物理现象、自然规律之间的内在联系达到较深刻的理解。数学能够简洁准确地表达物理概念与规律说明其为物理的一种语言，“如何运用数学语言在物理学中建构物理意义”好比人们“如何通过生活语言在人类活动中发现认知规律”。兴起于20世纪末的认知语义学在研究语言和人类认知世界之间的关系时提出了具身体验、百科观、语境等认知机制[4]，通过大学物理的教学与研究，我们发现，语言和人类认知世界之间的这些认知机制可以很好地映合到数学和物理规律认知的过程之中。

2.1 具身体验

具身体验强调通过身体结构、活动方式及其与环境的互动体验而形成认知[5]。语言中的“喜”“怒”“哀”“乐”可以通过人体的面部表情来认知，婴幼儿可以通过观察、触摸实物等方式来认识“皮球”“水”“水杯”等语义。通过具身体验在物理学中认知数学方法的物理意义，我们主要强调数学和物理之间的推理与类比，它不同于物理实验。通过物理实验活动认知物理现象，强调的是具身体验在物理科学与自然世界之间的相互作用。

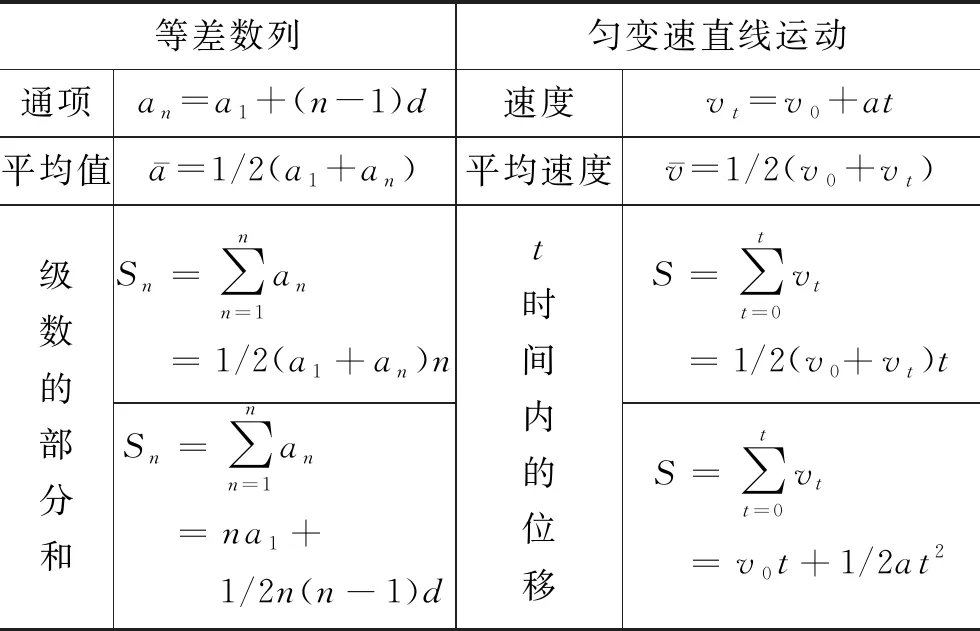
表1 数学中的等差数列与物理中的匀变速直线运动公式

2.2 百科观

认知语言学家Evans和Green明确提出意义表征具有百科性[4]。语义根植于语言使用者的百科知识体系中，应从使用者的认知结构、社会-文化背景知识等方面进行多维描述；反之，语义的理解也取决于语言接受者的认知结构、背景知识等[6]。同理，数学方法的意义建构根植于数学“语言”使用者或接受者的百科体系中，使用者或接受者的认知结构、社会-文化背景知识等方面的差异可能会令使用者或接受者为数学“语言”建构不同的物理意义，且建构过程是一个百科知识动态应用的过程。在下面的案例中，我们可以看到，对于同一个物理问题，不同的学生会采用不同的数学“语言”进行思考解答，反映出学生们认知结构、背景知识的差异性和百科性。

案例2： 调查对象：刚修完大学一年级第一学期课程的物理学专业本科生；调查方式：问答。

问题： 质量为M的物体在水平方向上与劲度系数为k的弹簧组成振子，以M的自然平衡位置O为坐标轴原点，若物体M在水平方向由原点移动至x位置处，如何求弹力对M做的功W？

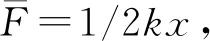
B同学： 首先需要外力对这个系统做功，物体的机械能不变，外力做的功转化为弹簧的弹性势能，外力拉物体，对物体做功，弹簧又对物体做负功，弹簧对物体做的功的负值就等于外力做的功，外力做的功的值等于弹簧的弹性势能，等于1/2kx2。

C同学： 弹力F=kx，那么W=Fx=kx2。但是M初始状态是在平衡位置，要想移动至x位置应该还得有拉力，看题意摩擦力应该是被忽略的，这样解好像有点简单了，所以我不太敢确定。(停顿)Ma=kx，W=1/2Mv2这样解出来是总的功，老师我觉得我还得再想想，或者老师能不能给些提示？(老师：考虑力和力的方向上的位移，拉力与解题无关，想一下高等数学里的积分。)F=kx，W=力对位移的积分=1/2kx2。

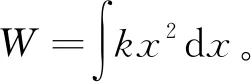
E同学： 可不可以直接用F-x图像，求面积就是做的功呀？(停顿)结果是1/2kx2？(老师：这么不自信？怎么求的？)(学生给出了下面的示意图，并问到：“我感觉这样也太容易就算出来了呀，所以，我对了吗？”)(老师：少了一个符号。)啥符号？(老师：负号。)对呦，负功。

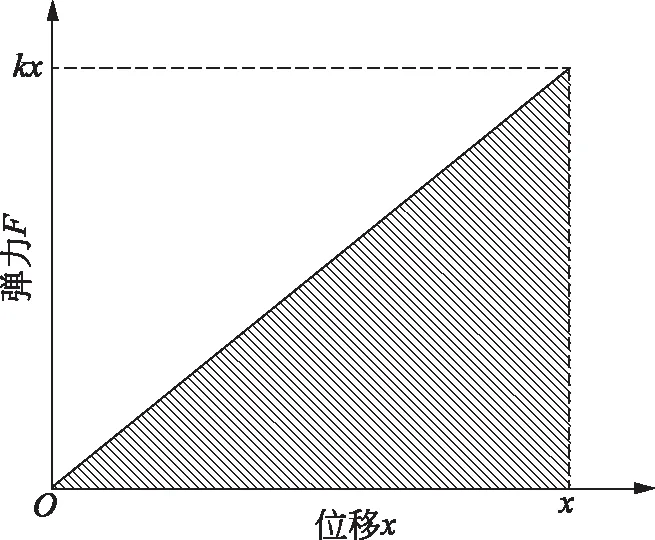
图1 E同学所建构的数学“语言”：求三角形的面积就是弹力对M做的功

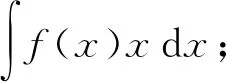
2.3 语境

人的大脑中储存了大量有关认知事物的百科知识，但在特定时间、特定语境下，认知者只能想到有限的相关知识，例如，案例2中出现的各种知识概念，5位同学都学习过，但每个人想到的知识结构不同，当然，他们的知识结构并非是固定不变的，在老师的提示下，学生的知识结构会发生迁移。认知语义学认为, 在外部刺激源如何被个体所认知的过程中，语境至关重要[4]，我们认为，在物理教学过程中亦是如此。在案例2中，学生们在联想外力时为什么会认为是“拉力”而不是“推力”(x完全可以是负值)？如果我们将问题中的“若物体M在水平方向由原点移动至x位置处”改为“若物体M在水平方向由x位置处移动至原点”，学生们是否还一定会想到“拉力”？再假设，如果我们不问学生们问题，只简单地给出一句陈述性描述“若物体M在水平方向由原点移动至x位置处”，学生们是否还会潜意识里认为x是正值？这说明，不同的语境线索会使学生对数学符号“x”产生不同的物理印象，但这种印象不一定是准确的。

数学方法在物理教学中的意义建构一般会涉及到4种基本的认知资源[7,8]：(1)计算 (Calculation)：在算法上不附加任何物理解释地进行一系列的数学计算而得到认为可信的结果。比如，老师在从d2h/dt2=-g推导出h=h0+v0t-1/2gt2的过程中可能不给学生讲解其中的任何物理过程，让学生们认为数学推导步骤是对的，所以结果也是可信的。(2)物理图像(Physical mapping)：一个简单的数学符号或几何模型可以丰富地表征物理意义。比如，弹力F=-kx中的负号可以通过一种物理图像“弹簧回复力的方向与振子位移的方向相反”得到解释，而无需进行任何数学上的证明。(3)权威 (Invoking authority)：通过权威性知识让学生信服。比如，老师在讲解转动惯量的相关知识时，让学生们直接看教材某页的某个表格，告诉学生实心球体的转动惯量I=2/5mR2，圆盘绕中心转轴的转动惯量I=1/2mR2…。(4)数学上的一致性 (Mathematical consistency)：数学方法具有一定规律性和可信性，对于不同的物理问题，背后隐藏的数学原理可能是一致的。比如，老师在讲解两个点电荷之间的库仑力 时，可能会提醒学生万有引力并解释两者之间的相似性，通过建立某种普适的数学原理让学生相信物理问题之间的相关性。

在对数学方法进行物理意义建构的过程中，还可能会受到学生经验直觉和主观情感的影响，而且在教学过程中，学生的认识论和意义建构是一个动态过程。Gupta和Elby的案例研究可以很好地说明学生的认识论和意义建构是如何受经验直觉和情感的影响而动态变化的[9]。

案例3： 老师问了工程系刚开始学习物理课程的一名学生Jim一个有关水面下压强的问题。老师先给Jim一个表达式P=P0+ρgh，并在确认Jim没有见过该表达式的前提下，告诉JimP0和P分别表示水面位置处和水面下深度为h处的压强，ρ和g分别为水的密度和重力加速度。然后让Jim根据公式判断水面下5m和7m位置处，哪个深度处的压强大，或者是否相等？Jim认为，从水面向下的方向应为坐标轴的负方向，所以h值均为负数，然后，Jim就陷入了各种犹豫、困惑和难以抉择，因为他发现数学计算的结果是水面下5m位置处的压强比7m位置处的大，但经验直觉又让他难以置信。后来老师提示Jim注意g的方向，然后Jim才明白g方向向下，所以也应该取负值，最后终于茅塞顿开。在随后的交谈中，Jim告诉老师，如果是在考试中，他可能会相信数学计算的结果而不是自己的经验直觉，因为Jim认为有时候人的直觉并不一定准确，可能会与自己所不知道的事实或者理论相悖。

图2(a)和(b)分别总结了Jim在难以抉择中和纠正错误后被激活的认知元素与思维活动。可以看出，Jim在难以抉择中用权威知识(老师给的压强计算公式)和数学计算建构的知识抑制住了自己从经验直觉中建构的知识，但又感到非常的“不安”和难以置信。后来在老师的提示下，Jim的经验直觉与计算和权威知识达到了一致，“不安”感得以消除。老师的语境线索使Jim从某一种认识论转移到了另一种认识论。

图2 Jim在(a)难以抉择中和(b)纠正错误后被激活的认知元素(实线椭圆)与思维活动(点虚线椭圆)，虚线椭圆表示控制元素，箭头和实圆点分别表示激活和未被激活的认知元素、思维活动、控制元素之间的关系，灰色表示被抑制

通过上述分析我们意识到，老师在教学过程中需要学会采用合适的语境引导学生在物理学中建构数学方法的物理意义。在案例2中，为什么高等数学中的微积分与物理学中的力学在同一个学期开设学习课程，但课程结束后，有些学生还停留在使用高中的知识处理物理问题？这说明他们仍视高中知识为“母语”而微积分为“外语”，帮助学生将高等数学转化为大学物理中的“母语”，需要高校教师在教学过程中通过合理的语境引导学生构建高等数学在大学物理中的意义，通过熟能生巧，让学生像“看到(x,y,z)就想到直角坐标系”一样找到数学方法在物理学中的应用，通过语境线索丰富学生的认识论与资源框架。

3 结语

本文通过分析物理学中的数学与纯数学的不同，并将“数学之于物理”与“语言之于生活”进行类比发现，认知语义学在研究语言和人类认知世界之间的关系时提出的具身体验、百科观、语境等认知机制，可以很好地应用于分析和发现大学生学习物理的认知过程以及数学方法在融入物理教学过程中存在的问题。案例分析亦表明，目前尽管大学教学中已经开设了很多有关高等数学的课程，但很多学生并不能在学到的数学方法与物理知识之间建立某种联系或做到知识的迁移。因此，在大学教学过程中，教师除了单纯地传授知识外，还应该多了解学生的学习状态，根据学生的百科知识，采用恰当的语境线索激发学生多样的认识论资源，通过推理与类比等具身体验，帮助学生自主学会数学方法在物理学中的意义建构与应用。