基于局部敏感性的平衡场长影响因素分析

张俐娜，王世涛，刘小川

(中航西飞民用飞机有限责任公司 工程技术中心，西安 710089)

0 引 言

起飞场长是衡量起飞性能的主要指标，是影响飞机起飞质量的重要因素。跑道长度较短，无疑会降低飞机的起飞质量，进而影响商载，降低运营效益。美国联邦适航标准(FAR)和我国民航适航标准(CCAR)都明确规定，民用飞机的起飞距离应取全发起飞距离的115%和起飞平衡场长(Balanced Field Length，简称BFL)两者当中较大者[1]。依据CCAR25、FAR25和JAR25的B部分，起飞场长取起飞距离、起飞滑跑距离和加速停止距离三者中最大值。因此，研究平衡场长具有重要意义。

研究平衡场长参数影响的敏感程度，可以定量地得知在给定工作状态下，各控制量对平衡场长参数影响的敏感程度，为控制平衡场长性能参数提供理论指导，同时通过分析平衡场长性能参数相对各控制量的灵敏度，可求得其影响最大和最小的控制量，定量地说明平衡场长性能参数相对控制量或外界干扰因素的敏感度，为性能试飞方案的确定以及控制参数的选择提供依据。H.G.Visser[2]研究了多发直升机平衡场长轨迹优化方法；向孙祖等[3]研究了CJ828大型客机平衡场长分析，主要从平衡场长的角度对大型客机的起飞性能进行估算分析；余俊雅等[4]在运输类飞机平衡场长的计算中主要论述了一种运输类飞机适航审定试飞平衡场长的确定方法；王建培等[1]研究了平衡场长的计算与影响因素分析，主要分析了民用飞机起飞过程，给出既能满足适航要求又便于工程分析的计算平衡场长的方法，并对“非平衡场长”下的起飞等使用情况进行了讨论。这些研究只给出所关注因素对平衡场长和决策速度的影响，没有对其参数的灵敏度进行分析研究。

本文以某型民用飞机为例，介绍平衡场长的计算流程及灵敏度分析理论，归纳平衡场长的影响因素：起飞质量、机场高度、风速、温度、跑道坡度，并探讨这五个影响因素对平衡场长的灵敏度。

1 平衡场长

在单发停车情况下，可能存在一个发动机失效速度VEF，使得单发停车加速停止距离与单发停车起飞距离相等。此时的VEF称为临界发动机失效速度，所得到的单发停车起飞距离或加速停止距离称为平衡场长。下面给出单发停车下起飞距离和加速停止距离的计算公式[5]。其中，单发停车起飞距离为：

Ldhf=LVW-VEF+LVEF-VR+LVR-VLOF+Ldks

(1)

式中：Ldhf为单发起飞距离；LVW-VEF为起飞开始点到一台发动机失效点的距离；LVEF-VR为发动机失效点到飞机抬前轮点的距离；LVR-VLOF为飞机抬前轮点到离地点的距离；Ldks为单发停车空中段距离。

单发加速停止距离为：

Ldjt=LVW-VEF+LVEF-Vsh+Lt

(2)

式中：Ldjt为单发加速停止距离；LVEF-Vsh为一台发动机失效点到踩刹车点的距离；Lt为踩刹车点到飞机停止的距离。

上述多个距离的具体计算方法见文献[5]，相关参数主要包括单台发动机推力、起飞质量、重力加速度、跑道坡度(上坡为正)、地面滑跑摩擦系数、升力系数、阻力系数、大气密度、机翼面积、滑跑速度、风速(逆风为正)、离地速度、飞行阻力、起飞安全高度、飞机到达安全高度时需要达到的安全速度、刹车速度和刹车摩擦系数。平衡场长的计算流程如图1所示。

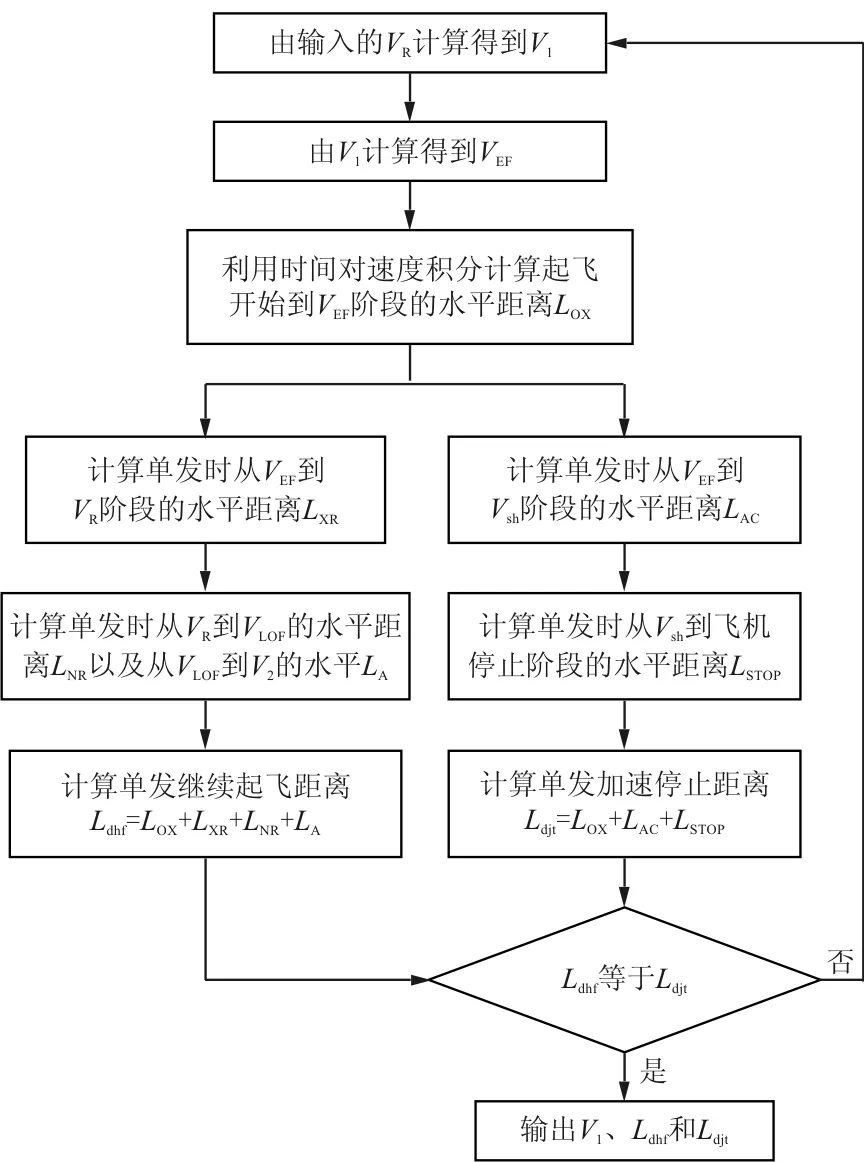
图1 平衡场长的计算流程

考虑到飞机安全因素，CCAR-25-R4[6]性能条款关注的是一台发动机停车时的飞机飞行性能。通常临界发动机停车速度(VEF)越大，则加速-停止距离(Acceleration Stop-go Distance，简称ASD)就越长，而起飞距离(Take-off Distance，简称TOD)就越短。

实际应用中，分析平衡场长问题时，大多不直接使用临界发动机停车时的速度，而使用决策速度来分析，考虑到飞行员从觉察停车，做出判断，到采取措施的时间滞后，CCAR-25-R4(§25.107 起飞速度)[6]规定，决策速度不得小于临界发动机停车速度，同时决策速度不得大于飞机的抬前轮速度VR。平衡场长BFL与决策速度V1的确定如图2所示。其中横坐标为飞机速度(km/h)，纵坐标为距离(m)，单发停车时，起飞距离和加速停止距离两条曲线的交点对应的横坐标为决策速度V1，纵坐标为平衡场长BFL。

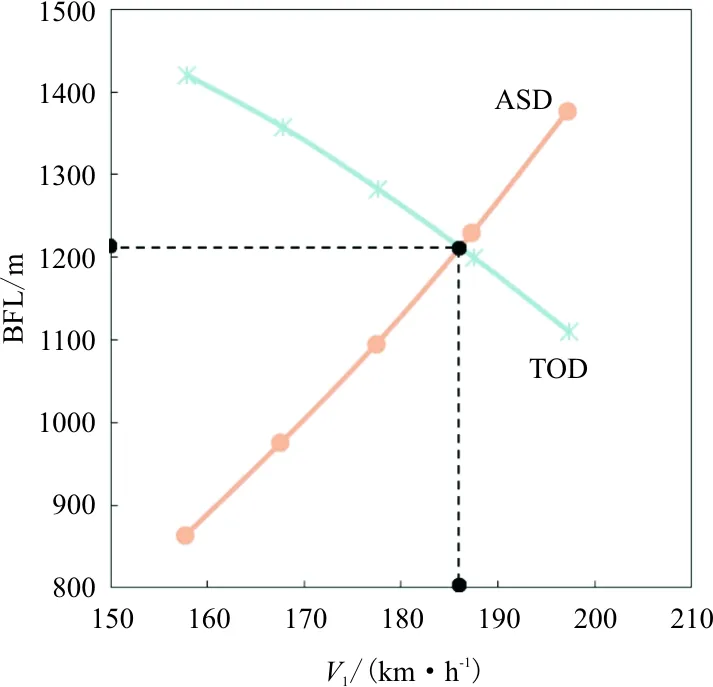
图2 平衡场长与决策速度的确定

起飞过程中，若临界发动机停车时的速度小于决策速度，则只能中断起飞。反之，若停车时的速度大于决策速度，则只能继续起飞。只有当停车时速度恰好等于决策速度，飞行员才能在中断起飞和继续起飞之中选择其一。由此可见，平衡场长是民用飞机设计和使用中的重要技术指标之一，它对民用飞机的经济性、安全性和通用性都有显著的影响。

2 参数敏感性分析理论

2.1 灵敏度分析

将BFL的理论公式归纳为如下形式：

BFL=f(x,y,z,…)

(3)

式中：x,y,z,…为影响BFL的各个参数。

其中，参数x灵敏度是F对x的偏导数：

(4)

通常，灵敏度Sx,1的绝对值越大，表示参数x对BFL的影响越显著。

计算BFL时涉及的参数较多，若直接根据式(4)推导每个参数的灵敏度，则计算过程复杂，不便于工程应用。因此，这里采用中心差分法[7]对式(4)进行数值逼近，可使灵敏度达到二阶精度：

(5)

式中：Δx为参数x的波动小量。

由式(5)可知：不同参数灵敏度的量纲不同，不便于比较各个参数对BFL影响的重要程度。

2.2 绝对变化量分析

将灵敏度Sx,1乘以参数x本身，可得参数敏感性分析的另一种表达式：

(6)

同样采用中心差分法对式(6)进行数值逼近，可得

Sx,2

(7)

通常Δx为参数x的比例小量，令Δx=δ·x，此时，式(7)变为放大1/δ倍的BFL绝对变化量。

采用式(7)衡量不同参数的敏感性时，所得结果的量纲完全相同，与BFL量纲一致。

2.3 相对变化量分析

BFL的绝对变化量除以BFL本身，可得参数敏感性分析的相对变化量：

(8)

此时参数Sx,3为无量纲量。

由上述理论分析可知，式(7)和式(8)所示的敏感性分析表达式量纲统一，便于对比分析不同参数对BFL影响的重要度。

3 算 例

3.1 影响因素分析

以某型民用飞机为例，分析一些关注因素对平衡场长的影响。计算参数及其初始值主要有：飞机起飞质量24 000 kg，机场起飞安全高度10.7 m，跑道为干水泥跑道，跑道坡度0°，起飞襟翼17°，风速0 m/s，机场标高1 000 m，大气温度ISA+15 ℃。

3.1.1 起飞质量的影响

计算时，只改变起飞质量，其他参数不变，研究起飞质量变化对平衡场长的影响，分析结果如图3所示。

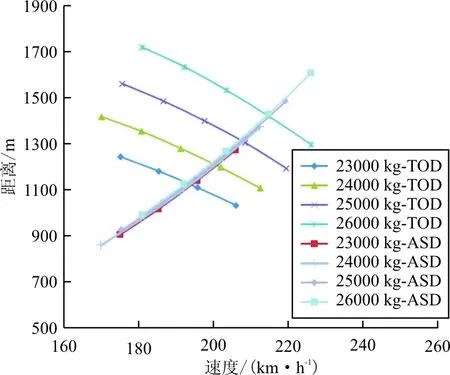
图3 起飞质量对平衡场长的影响

从图3可以看出：起飞质量从23 000 kg增加到26 000 kg时，起飞距离曲线平行上移，加速停止距离曲线也增加，但变化趋势不太明显。同时，起飞质量增加时，平衡场长和决策速度都会明显增加。

3.1.2 机场高度的影响

计算时，仅机场高度变化，其他参数不变，研究机场高度变化对平衡场长的影响，分析结果如图4所示。

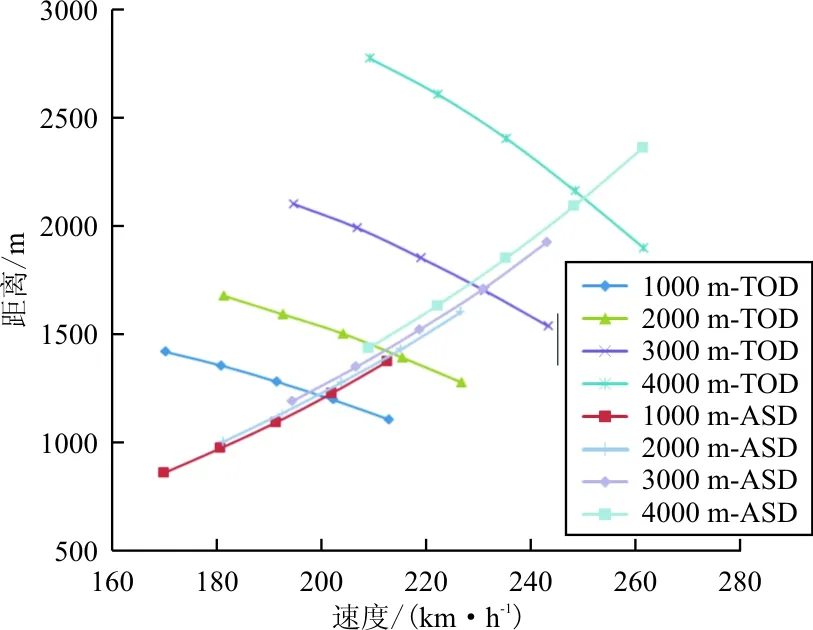
图4 机场高度对平衡场长的影响

从图4可以看出：机场高度等高度增加，平衡场长增大，且增加速度越来越快。分析原因在于：随着机场高度增加，空气密度降低，发动机功率减小，发动机推力减小，起飞距离增加，加速停止距离增加，因而平衡场长和决策速度均增大。

3.1.3 风速的影响

沿跑道方向，假设逆风为正，顺风为负，例如，-10 kts表示大小为10 kts的顺风风量。飞机及机场信息不变，计算风速-10、-5、0、5、10 kts对应的平衡场长，风速对平衡场长的影响如图5所示。

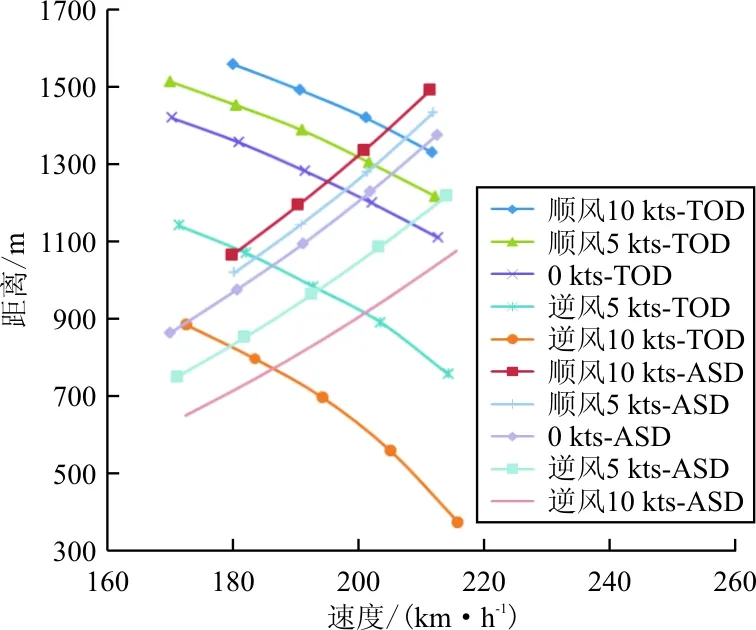
图5 风速对平衡场长的影响

从图5可以看出：逆风时，随着风速的增加，平衡场长和决策速度均减小；顺风时，随着风速的增加，两者均增加。

3.1.4 温度的影响

计算时，只改变温度，其他参数不变，温度对平衡场长的影响如图6所示。

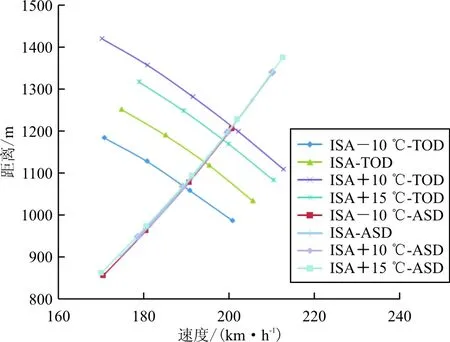
图6 温度对平衡场长的影响

从图6可以看出：温度增加时，起飞距离曲线增加，加速停止距离曲线变化趋势不明显。同时，随着温度的增加，平衡场长和决策速度均增加。分析原因在于：同一高度下，温度增加，发动机推力减小。

3.1.5 跑道坡度的影响

飞机及其他机场信息不变，计算跑道坡度分别为-1.0%、-0.5%、0%、0.5%时的平衡场长，分析结果如图7所示。

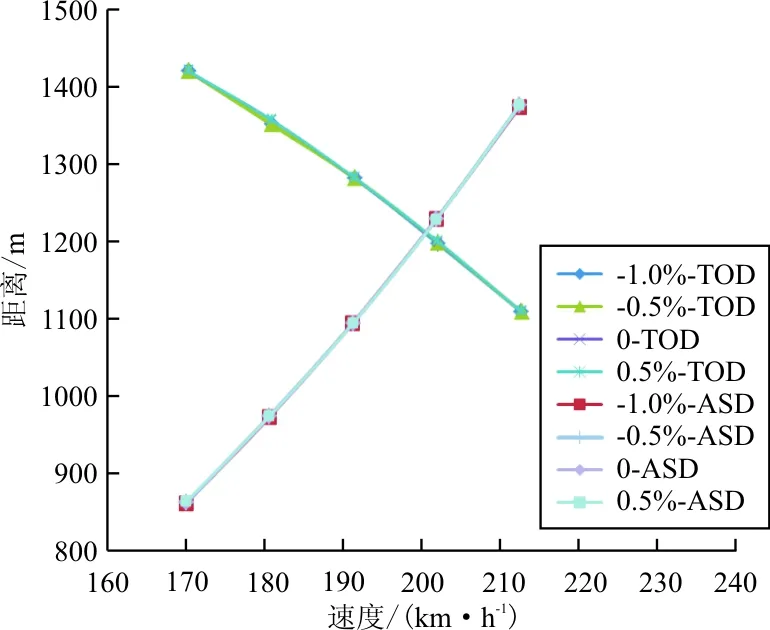
图7 跑道坡度对平衡场长的影响

从图7可以看出：跑道坡度变化时，起飞距离曲线和加速停止距离曲线几乎没有变化，换言之，跑道坡度基本不影响平衡场长。

3.2 参数敏感性分析

根据第2节介绍的三种参数敏感性分析理论方法，对影响平衡场长的关键参数进行分析。飞机起飞质量为24 000 kg，机场起飞安全高度10.7 m，跑道为干水泥跑道，跑道坡度0.005°，起飞襟翼17°，风速2.57 m/s，机场标高1 000 m，大气温度ISA+15 ℃。敏感性分析结果如表1所示。对比三种方法对参数敏感性的分析结果可以看出：三种方法对于参数的正负相关性是一致的，正值表示正相关，即该值增加时，BFL值增加；负值表示负相关，即该值增加时，BFL减小。计算结果与3.1节的影响规律一致，这5个变量对BFL的敏感性排序为：起飞质量>风速>机场高度>温度>跑道坡度。方法一中各参数的灵敏度的量纲并非完全相同，导致分析结果差别较大；方法二和方法三的分析结果趋势一致，但方法三的敏感性数值较小，不便于直观比较。因此，建议采用方法二进行绝对变化量分析，将单位不同的参数进行量纲统一化，分析效果较好。

表1 敏感性分析结果

4 结 论

(1) 平衡场长和决策速度随起飞质量、机场高度、顺风风速、温度的增加而增加；平衡场长和决策速度随逆风风速的增加而减小，跑道坡度对平衡场长的影响几乎可以忽略。

(2) 三种方法对于参数的正负相关性是一致的，这5个变量对平衡场长BFL的敏感性排序为：起飞质量>风速>机场高度>温度>跑道坡度。

(3) 方法二的量纲统一，敏感性数值相对方法三比较直观，分析效果较好，建议采用方法二绝对变化量进行分析。