产业结构偏离、城市化与城乡收入差距

葛玲玲

摘 要：在厘清产业结构偏离、城市化与城乡收入差距之间关系的前提下，重点分析在此系统中影响城乡收入差距的途径。研究发现，产业结构偏离度（产业结构优化）与城市化形成良性互动可以缩小城乡收入差距，而城市化不可以直接缩小城乡收入差距，它是通过产业结构偏离度的减小来间接缩小城乡收入差距的。其中，产业结构偏离度的缩小（产业结构的优化）是重点，其带来的正效应最为深远。

关键词：产业结构偏离;城市化;城乡收入差距;VECM模型

中图分类号：F299.2        文献标志码：A      文章编号：1673-291X（2019）15-0137-03

一、问题背景

自改革开放以来，我国经济发展取得举世瞩目的成绩。国民收入年增长率一度以两位数持续增长，被称为中国式增长奇迹。1978—2016年，国内生产总值的增加值分别为827 391.7亿元和3 678.7亿元。其中，农业国内生产总值年平均增长率从1952—1978年的2.2%提高到1978—2016年的4.5%[1]。经济飞速发展的背后，是城镇化与产业结构不断推进与完善。据国家统计局有关数据，我国城镇化率继2011年首次突破 50%以后，2012年我国城镇化率已达52.6%[2]，我国城镇化程度已经超过世界城镇化的平均水平[3]。城镇化通过要素积累、需求集中、分工和专业化途径[4]，来刺激消费、拉动投资、优化产业、创新激励等机制促进经济增长[5]及农民收入增长[6]。城市不断吸引相对分散的资源要素，获得规模及集聚效应。在要素不断分配、再分配過程中，实现资源配置效率的提高和产业结构的优化。不断升级的产业结构吸纳更多的资源，释放了更多的要素价值，促进经济增长，推动城市化进程。

产业结构调整对城乡收入分配的效应源于产业结构调整会使就业结构发生变化[7]，导致产业间劳动生产率及非农收入的提高，从而影响农村居民家庭人均收入进而影响城乡收入差距。高霞运用协整理论和Granger因果检验分析发现，中国产业结构变动和城乡收入差距存在长期稳定的正向均衡关系，短期动态校正作用明显，且两者存在双向因果关系[8]。由于所有制结构与产业结构的不匹配[9]、政策偏向例如优先发展重工业[10]等，导致了城乡收入差距的扩大，因此，在注重速度与效率的原则下，优化产业结构是重点。有些学者认为，城镇化与城乡收入差距具有互动关系，并非简单的线性关系，例如史云鹏等[11]、王亚飞等[12]。

从我国实践来看，三者之间有着密不可分的关系。杨松和王爱峰利用江苏省的经济数据，通过多元线性回归和分位数回归进行实证研究发现，城市化和产业结构都对城乡收入差距有扩大作用[13]。部分学者认为三者之间不是简单的线性关系，穆怀中等利用借鉴巴罗的内生经济增长模型，理论上证明了存在二次函数关系[14]。通过实证得出的结论是，城镇化水平与城乡收入差距呈现“倒U型”关系;产业结构调整与城乡收入差距呈现“倒U型”关系，并得出2009—2015年是城乡收入差距缩小的关键时期。相关的研究还有郑许海等[15]、林毅夫等[16]。

本文通过梳理以上文献发现，城乡收入差距、城镇化、产业结构之间有繁杂、交错的作用路径，将三者同时纳入一个分析框架（模型）更具有现实意义。而很多学者把研究的重点主要集中在两者之间的关系上，本文作为补充，将三者同时放入VEC模型中进行探讨。另一方面，本文采用产业结构的偏离度来度量产业结构优化，使得分析结论更具科学性。在此基础上，运用VAR模型厘清三者的之间的关系及相关作用路径，为我国后来经济的发展找到改进方向，以加速当前经济的发展，避免落入“中等收入陷阱”。

二、研究方法介绍

（一）指标选取

本文的城乡收入差距表示为城镇居民人均可支配收入与农村居民人均纯收入的比值。城镇化用具有城镇户籍的人口与非城镇户籍人口的比值来度量。重点介绍的是产业结构偏离计算方法，与已有文献有所区别。大部分文献产业结构的表示方法：分别用第一产业产值、第二产业产值、第三产业产值与总产值的比值来表示[8，13，15]。而本文借鉴牛凯[17]的方法，采用产业结构的偏离度来度量，这种偏离度计算原理实质为，产业结构本身与就业结构的相对偏离值，以下是计算的一般步骤：

1.产业结构表示为：

INi=AiA

2.就业结构表示为：

JYi=DiD

3.相应的产业偏离度为：

Ei=（INi-JYi）/INi

4.总体偏离度为：

E=E1+E2+E3

其中，A1表示第一产业产值（亿元）;A2表示第一产业产值（亿元）;A3表示第一产业产值（亿元）;A表示总产值（亿元）;D1表示第一产业从业人口（万人）;D2表示第二产业从业人口（万人）;D3表示第三产业从业人口（万人）;D表示三产业从业总人口（万人）。其中，i=1，2，3分别表示第一产业、第二产业、第三产业。

（二）方法介绍

在三者错综复杂的关系中，并没有明确因果关系的方向性，为此本文运用VAR模型进行分析。该模型可以有效处理具有内生关系的变量，通过联立各变量自回归方程，将变量纳入一个系统中，相互自恰以提高模型估计的有效性。

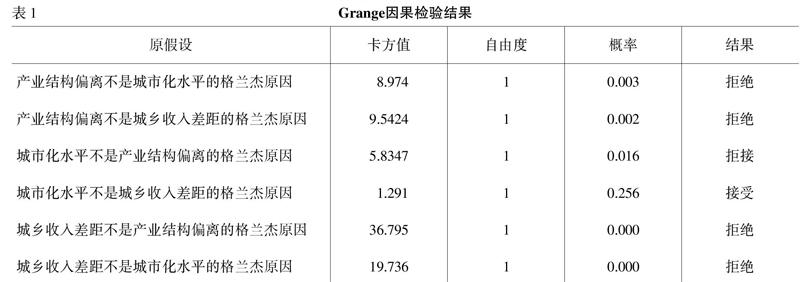
1.Granger因果分析。在时间序列的数据中，格兰杰因果检验只是动态相关关系。它的原理主要是利用变量X过去的信息来解释当前的Y，如果可以解释，说明X是Y的格兰杰原因。否则，X就不是Y的格兰杰原因;同理，可验证Y是否是X的格兰杰原因。

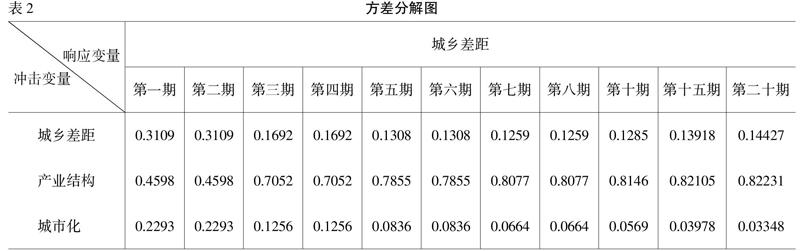
2.方差分解。方差分解描述的是上述外部冲击给VECM模型中各变量带来的动态变化以及造成这种变化在不同时期各变量相对重要性，以估计出各变量的相对大小。主要思想是将系统的预测均方误差按其成因分解为：自身冲击、其它变量冲击所构成的贡献率，从贡献率的大小看出变量的相对重要性，同时观察变量的时滞效应。