一种面向云计算服务供应链的安全评估模型

刘垚磊　陈兴蜀　李想　王启旭

摘   要：针对云计算服务供应链中存在的安全问题，提出了一种安全评估模型。首先，将供应链风险识别方法与云计算服务场景相结合，识别出了云计算服务供应链的主要风险目标及其风险来源事件集，并以国标《云计算服务安全能力要求》为基础，构建了安全指标体系;其次，考虑到云计算服务供应链的动态开放、复杂多变以及大多安全指标无法量化的特点，设计了基于德尔菲方法的风险来源度量流程和权重赋值流程，并提出了基于模糊综合评价的安全评估流程，以实现风险来源的风险等级度量结果的一致性;最后，通过一个应用实例验证了安全评估模型的有效性和可行性。

关键词：云计算服务;供应链安全评估;德尔菲法;层次分析法;模糊综合评价

中图分类号：TP399          文献标识码：A

A security assessment model for cloud computing service supply chain

Liu Yaolei1，3， Chen Xingshu2，3， Li Xiang1，3，Wang QiXu2，3

（1.College of Computer Science，Sichuan University， SichuanChengdu 610065;

2. College of Cybersecurity， Sichuan University， SichuanChengdu 610065;

3. Cybersecurity Research Institute， Sichuan University， SichuanChengdu 610065）

Abstract： A security evaluation model was proposed to solve the security problems in the supply chain of cloud computing services. Firstly， combining the supply chain risk identification method with the cloud computing service scenario， the main risk objectives and risk source event sets of the cloud computing service supply chain were identified， and the security index system was constructed based on the cloud computing service security capability requirements which is national standard. Secondly， considering the dynamic open， complex and changeable characteristics of cloud computing service supply chain， and most security indicators can not be quantified， the risk source measurement process and weight assignment process based on Delphi method were designed， and a safety assessment process based on fuzzy comprehensive evaluation was proposed to achieve the consistency of risk level measurement results of risk sources. Finally， an application example verified the validity and feasibility of the security evaluation model.

Key words： cloud computing services; supply chain security assessment; Delphi; analytic hierarchy process; fuzzy comprehensive evaluation

1 引言

随着云计算的快速发展，安全问题已成为影响其进一步发展的主要障碍[1]。供应链安全作为云计算安全的关键环节，一旦出现问题，能够直接影响云计算服务的质量，甚至导致云计算服务的中断。因此，有必要通过对云计算服务供应链安全评估的研究，及时了解其安全状态。

当前，针对云服务安全能力评估的研究通常是针对云服务商选择的场景，构建安全指标体系或利用现有的安全指标，提出安全评估方法，对云服务商的安全能力进行评估[3-5]。供应链安全评估的研究以通用供应链为基础：一方面是对供应链中的潜在风险进行识别，并在此基础上提出风险评估与管理方法[6，7];另一方面是针对供应商选择的场景，构建安全指标体系并提出安全评估方法，对供应商的安全能力进行评估[8，9]。

然而，上述研究通常只提供一些通用的風险评估模型和方法，缺乏对云计算服务供应链深入的分析与研究。因此，从安全评估的角度来说，当前仅针对云服务安全或供应链安全的研究并不能完全满足云计算服务供应链的实际场景需求。

针对上述问题，本文在对云计算服务供应链深入分析的基础上，结合国家标准GB/T31168-2014《云计算服务安全能力要求》[2]的内容，提出了面向云计算服务供应链的安全评估模型，用以评估其不同指标层次的风险等级，获得一个全方位的风险状态视图，并通过应用实例验证了安全评估模型的有效性及可行性。

2 相关研究

由于目前缺少针对云计算服务供应链安全评估的研究，因此本文从云服务安全评估和供应链安全评估两个方面来阐述其研究现状。

在云服务安全评估方面，已有许多学者进行了大量的研究。Jiang等人在服务水平协议SLA（the Service Level Agreement）的基础上，利用目标问题度量GQM（Goal Question Metric）构建了指标集[3]，并通过计算每个云服务商与“最好”的距离、与“最差”的距离以及与“客户需求”的距离得到其安全能力得分。Li等人直接使用云控制矩阵CCM（Cloud Control Matrix）中的安全指标，通过TOPSIS（Technique for Ordering Preference by Similarity to Idea Solution）计算候选云服务商的安全能力得分[4]。Liu等人在客观方面，采用来自于QoS（Quality of Service）属性的监测值，主观方面参考的是用户的信任偏好，利用TOPSIS方法对主客观信息进行处理进而得到云服务商的安全能力得分[5]。

在供应链安全评估方面。一方面，有不少学者从供应链整体出发，研究风险评估与管理的方法。Rao将供应链风险管理分为五个步骤，分别是风险识别、风险度量、风险评估、风险评价以及确定风险接受度[6]。Abroon等人使用贝叶斯网络和故障分析树方法对供应链进行风险识别，并利用期望效用理论评估风险因素对绩效指标的影响[7]。另一方面，很多学者针对供应商选择的场景开展研究。Tobias等人讨论了一家美国制造公司为两条主要产品线寻找新供应商的问题，一共有5个备选方案需要考虑。他们首先确定了17个风险因素，然后将其分为主要目标和次要目标，用层次分析法评估每个风险因素的重要性，并确定最佳方案[8]。Shanmugam等人讨论了在中断风险下供应商的最优选择和订单数量分配问题。他们利用多目标粒子群优化方法，给出了供应商选择和订单分配的一组帕累托最优解[9]。

3 安全评估模型

本文在对云计算服务供应链深入分析的基础上，提出了面向云计算服务供应链的安全评估模型，具体分为四个部分，如图1所示。

（1） 构建安全指标体系。本文构建了用于云计算服务供应链安全评估的指标体系及其交付件列表。安全指标体系用于评估云计算服务供应链不同指标层次的风险等级;交付件列表用于收集安全指标相关信息。

（2） 权重赋值。在本文的安全评估模型中，需要对安全指标体系中的一级指标和二级指标赋予权值。

（3） 风险来源度量。风险来源是安全指标体系中的二级指标，它的风险等级度量是对云计算服务供应链进行安全评估的基础。

（4） 安全评估。评估云计算服务供应链不同指标层次的风险等级。

本节将会对这四个部分进行详细描述。

3.1 安全指标体系

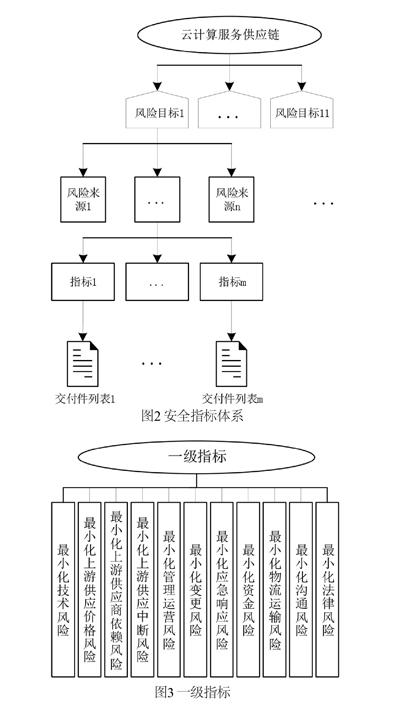
本文首先将“价值聚焦的供应链风险识别方法”[10]应用到云计算服务供应链场景中，识别出了云计算服务供应链的的主要风险目标及其风险来源事件集;然后将风险来源事件集和国家标准GB/T_31168-2014《云计算服务安全能力要求》中的内容相结合，制定了风险来源事件的下级指标，并设计了交付件列表，用于收集安全指标相关信息。风险目标、风险来源事件集及其下级指标分别作为一级、二级和三级指标构成了云计算服务供应链安全评估的安全指标体系，如图2所示。一级指标的内容如图3所示。

3.2 风险来源度量

本文采用的是Neil等人在1986年提出的风险等级分类方法[11]。他们根据后果严重程度将风险等级分为四类，下文中分别将其记作B、C、D、E。其中，E对应大的风险，D对应中等的风险，C对应小的风险，B对应微不足道的风险。为了更加符合风险评估的实际情况，本文增加一个新的等级A，A等级代表云服务商的安全控制措施非常完善，不存在任何风险。

在云计算服务供应链安全评估的场景中，大多安全指标无法量化，且难以获取历史信息。因此，在利用交付件列表获取三级指标相关信息后，本文采用德尔菲方法[12]对每个风险来源进行风险等级度量。

需要注意的是，对于同一个风险来源，尽管每个专家只能给出一个风险等级评估结果。然而，由于专家知识经验的差异性，对于同一个风险来源，不同的专家给出的风险等级存在不一致性。因此，同一个风险来源的风险等级度量结果可能是A、B、C、D、E中的几种，但这并不会影响后续的安全评估工作。

3.3 权重赋值

在本文的安全评估模型中，需要为一级指标和二级指标赋权。如图4所示，权重赋值分为确定初步权重和确定最终权重两步。

（1） 确定初步权重

针对云计算服务供应链的动态开放、不确定因素多等特点，本文通过德尔菲方法获取安全指标的初步权重。这里规定同一域指标的相对重要度用数字1～9表示，数字越大表示指标越重要。同一域指的是同一个一级指标下所有的二级指标或所有的一级指标。具体分为几个步骤。

1） 组建专家小组和监督小组。选取云计算、供应链、风险评估、社会管理等领域的专家若干，组建专家小组和监督小组。专家小组应由若干個小组构成，每个小组中包含每个领域的专家至少一名;监督小组应包含每个领域的专家至少一名。

2） 设计调查问卷。监督小组依据一级、二级指标及其它相关材料设计调查问卷，调查问卷中应包含其所掌握的所有有助于确定指标权重的信息。

3） 专家小组评估权值。专家小组在接收到调查问卷后，其中的每个小组应独立地依据调查问卷对指标权重值进行评估。

4） 回收结果。监督小组在收到专家小组的反馈后，对反馈结果进行总结并修改调查问卷为下一轮的评估做准备。重复步骤2～4，直至专家小组的反馈结果趋于一致。

5） 在完成以上步骤后，监督小组需要找出每个指标权重评估结果的众数，将其作为指标的初步权重值。

（2） 确定最终权重

经过确定初步权重环节后，每个指标都有一个初步权重值，用1～9表示，如表2所示。

通过AHP[13]方法对一级指标和二级指标的初步权重值做进一步的处理，可得到它们的最终权重值。在计算最终权重时，需要多次使用AHP方法。每次AHP方法的作用范围都是同一域内的指标，同时计算出同一域内所有指标的最终权重值。本文以第一个一级指标下所有二级指标为例，计算它们的最终权重值。首先建立决策矩阵如公式（1）所示。

（1）

假如第一个一级指标下有个二级指标，则这个二级指标的决策矩阵大小为。Ai，j的计算方法如公式（2）所示。

（2）

其中，M1，i是该一级指标下第i个二级指标的初步权重值，M1，j是该一级指标下第j个二级指标的初步权重值。对得到的决策矩阵求解最大特征值及其对应的特征向量，并使用公式（3）对决策矩阵做一致性检验。

（3）

CI的计算方法如公式（4）所示，RI的值可通过查表获得。

（4）

其中，λmax是决策矩阵的最大特征值，n是该一级指标下二级指标的数量。

当n的值大于12时，可通过文献[14]中介绍的方法计算RI的值。一般情况下，当CR的值小于0.1时，认为决策矩阵符合一致性检验;否则，需要对决策矩阵调整后重新进行以上步骤。假设最大特征值对应的特征向量为η，如公式（5）所示。

（5）

对特征向量中的元素值进行归一化即可得到该一级指标下所有二级指标的最终权重值，如公式（6）所示。

（6）

至此，第一个一级指标下所有二级指标的最终权重值已经计算完毕。使用以上步骤可计算出其它一级指标下二级指标的最终权重值和所有一级指标的最终权重值。

3.4 安全评估

由于专家知识经验的差异性，风险来源的风险等级度量结果存在不一致性。针对这种情况，本文采用基于模糊综合评价法的安全评估流程评估云计算服务供应链的风险等级，如图5所示。

（1） 建立模糊集

设={S1，S2，…，Sn}表示云计算服务供应链一级指标的集合，其中，n是一级指标的个数;i={Si，1，Si，2，…，Si，m}表示第i个一级指标下二级指标的集合，m为第i个一级目标下的二级指标个数;P={A， B， C， D， E}表示风险等级集，A， B， C， D， E分别代表不同的风险等级。

（2） 计算二级指标隶属度

可通过公式（7）计算指标Si，j对第s个风险等级的隶属度。其中，rs表示在风险来源度量结果中，有rs份调查问卷对指标Si，j的评估结果是第s个风险等级。s是风险等级集的下标。

（7）

（3） 各级指标权重

指标的权重值可参考3.3章节的方法得到，这里只描述如何表示各级指标权重值。

令W=（w1，w2，… ，wn）表示一级指标的权重向量，其中n是一级指标的数量;Wi=（wi，1，wi，2，… ，wi，m）表示第i个一级指标下二级指标的权重向量，其中m是第i个一级指标下二级指标的数量。

（4） 计算二级指标风险等级

设二级指标Si，j的隶属度向量如公式（8）所示。

（8）

其中，θi，j，1是二级指标Si，j对第一个风险等级的隶属度，即对风险等级A的隶属度，其它以此类推。利用最大隶属原则计算二级指标Si，j的风险等级。

（9）

其中，max（）函数代表取隶属度最大的风险等级。同理，使用以上步骤可计算出其它二级指标的风险等级。

（5） 构建二级指标评估矩阵

利用一级指标Si下所有二级指标的隶属度向量可构建出一级指标Si下二级指标的评判矩阵。评判矩阵中的每一行都是Si下一个二级指标的隶属度向量。

（10）

（6） 计算一级指标隶属度

利用公式（11）计算第i个一级指标的隶属度向量。其中，Wi是第i個一级指标下二级指标的权重值向量，θi.1是第i个一级指标对第一个风险等级的隶属度，即对风险等级A的隶属度，其它以此类推。

（11）

（7） 计算一级指标风险等级

第i个一级指标的风险等级可用公式（12）计算。其中，max（）函数代表取隶属度最大的风险等级。同理，使用以上步骤可计算出其它一级指标的风险等级。

（12）

（8） 构建一级指标评估矩阵

利用所有一级指标的隶属度向量可构建一级指标的评判矩阵。其中，评判矩阵中的每一行都是一个一级指标的隶属度向量。

（13）

（9） 计算整体隶属度

通过一级指标的权重向量和评判矩阵计算整体隶属度。其中，θ1是云计算服务供应链整体对第一个风险等级的隶属度，即对风险等级A的隶属度，其它以此类推。

（14）

（10） 计算整体风险等级

同理，可利用最大隶属原则对云计算服务供应链的整体风险等级进行认定。V即是云计算服务供应链整体的风险等级。

（15）

4 可行性分析

本节将通过一个应用实例验证本文所提出的安全评估模型的有效性和可行性。实验所使用的风险来源度量结果、指标的初步权重值均由随机数产生。由于本文对专家小组针对风险来源的度量结果以及指标的初步权重值进行了规范化，实际环境中数据的格式和实验数据是一样。因此，本节采用随机数进行的实验仍能够有效地验证安全评估模型的有效性和可行性。

（1） 权重赋值

这部分内容直接从初步权重值入手，利用AHP方法对初步权重值作进一步处理得到最终权重值。首先计算第一个一级指标下所有二级指标的最终权重。假设这些二级指标的初步权重向量如下所示。

可建立决策矩阵如下。

运用求和法可解得该决策矩阵的最大特征值及其对应的特征向量。

对决策矩阵进行一致性检验，首先计算CI的值。

查表可知，n=11时，RI的值为1.52。经计算，CR的值小于0.1，该决策矩阵符合一致性要求。由于向量η中的各个元素值已经满足归一化要求，因此，它的元素值可直接作为第一个一级指标下二级指标的最终权重值。同理，可计算出其它二级指标的最终权重值和所有一级指标的最终权重值。其中，第一个一级指标下二级指标的权重向量和一级指标的权重向量如下所示。

（2） 安全评估

1） 建立模糊集

设={S1， S2， …， S11}代表一级指标的集合;i={Si，1， Si，2， …， Si，m}代表第i个一级指标下的二级指标集合，m是第i个一级指标下二级指标的数量;P ={A， B， C， D， E}代表风险等级集。

2） 计算二级指标隶属度

第一个一级指标（最小化技术风险）下所有的二级指标如图6所示。以第一个一级指标下的二级指标（风险来源）为例，假设参与风险度量工作的专家小组有10个小组，度量结果如表4所示。表格中风险来源列的数字表示该一级指标下第几个风险来源，如2代表风险来源“缺少系统性的评估制度”。表格中其它列的数字表示有多少个专家小组对该风险来源给出了对应的风险等级。如第一个风险来源这一行与A等级这一列相交处是1，代表有一个专家小组对该风险来源的风险度量结果是等级A。

由此，可计算出第一个风险来源对应各个风险等级的隶属度向量。

同理，可计算出其它二级指标对应各个风险等级的隶属度向量。

3） 各级指标权重

前文已经计算出各级指标权重，这里只描述如何表示。令W=（w1， w2， … ，wn）表示一级指标的权重向量，其中n=11;Wi=（wi，1， wi，2， … ， wi，m）表示第i个一级指标下二级指标的权重向量，其中m是第i个一级指标下二级指标的数量。

4） 计算二级指标风险等级

利用最大隶属原则计算二级指标的风险等级。

因此，第一个一级指标下第一个二级指标的风险等级为B。通过以上步骤可计算出第一个一级指标下其它二级指标的风险等级以及其它一级指标下二级指标的风险等级。

5） 构建二级指标评判矩阵

利用第二步计算出的第一个一级指标下所有二级指标的隶属度向量，可构建出第一个一级指标下二级指标的评判矩阵。

6） 计算一级指标隶属度

第一个一级指标的隶属度向量如下。

其中，W1是该一级指标下二级指标的权重值向量。同理，可计算出其它一级指标的隶属度向量。

7） 计算一级指标风险等级

同样地，通过最大隶属原则计算一级指标的风险等级，以第一个一级指标为例。

因此，第一个一级指标的风险等级为B。

8） 构建一级指标评判矩阵

同样地，利用所有一级指标的隶属度向量可构建一级指标评判矩阵。

9） 计算整体隶属度

其中，W是一级指标的权重值向量。

10） 计算整体风险等级

因此，云计算服务供应链的整体风险等级为C。至此，云计算服务供应链的安全评估工作已全部完成，可以得到整体、一级指标和二级指标的风险等级，如图7所示，全方位了解云计算服务供应链的安全状态。

5 结束语

随着云计算产业的发展，云计算服务供应链网络日益复杂，也带来了许多安全问题。因此，有必要开展对云计算服务供应链的安全评估工作，及时了解其安全状态。本文针对这种情况，提出了面向云计算服务供应链的安全评估模型，通过对云计算服务供应链的风险分析与识别，结合国家标准的要求，构建了安全指标体系及其交付件列表;通过基于德尔菲方法的风险来源度量方法和权重赋值方法可以获取二级指标的风险来源度量结果及一级、二级指标的权重值;通过基于模糊综合评价方法的安全评估流程解决风险来源的风险度量结果可能存在不一致性的问题，并评估云計算服务供应链不同指标层次的风险等级。通过一个实例分析，验证了本文提出的安全评估模型的有效性和可行性。

基金项目：

1.国家自然科学基金资助项目（项目编号：61802270，61802271）;

2.中央高校基础研究经费（项目编号：SCU2018D018，SCU2018 D022）。

参考文献

[1] Basu S， Bardhan A， Gupta K， et al. Cloud computing security challenges & solution-a survey [C]//2018 IEEE 8th Annual Computing and Communication Workshop and Conference （CC-WC）. IEEE， 2018： 347-356.

[2] 陈兴蜀，左晓栋. GB/T 31168-2014，信息安全技术 云计算服务安全能力要求[S].北京：中国标准出版社，2014.

[3] Zhengwei J， Ran D， Zhigang L， et al. A meta-synthesis approach for cloud service provider selection based on secsla[C]//Computational and Information Sciences （ICCIS）， 2013 Fifth International Conference on， 2013：1356-1360.

[4] Li X ， Jin X ， Wang Q ， et al. SCCAF： A Secure and Compliant Continuous Assessment Fra- mework in Cloud-Based IoT Context[J]. Wireless Communicatio-ns and Mobile Computing， 2018， 2018：1-18.

[5] Lu L， Yuan Y. A novel TOPSIS evaluation scheme for cloud service trustworthiness combining objective and subjective aspects[J]. Journal of Systems and Software， 2018：71-86.

[6] Tummala R， Schoenherr T. Assessing and managing risks using the Supply Chain Risk Mana- gement Process （SCRMP）[J]. Supply Chain Managem-ent， 2011，16（6）：474-483.

[7] Qazi A， Dickson A， Quigley J， et al. Supply chain risk network management： A Bayesian belief  network and expected utility based approach for managing supply chain risks[J]. International Journal of Production Economics， 2018，196： 22-42.

[8] Schoenherr T， Tummala V M R， Harrison T P. Assessing supply chain risks with the analytic hierarchy process： Providing decision support for the offshoring decision by a US manufacturing company[J]. Journal of Purchasing and Supply Management， 2008， 14（2）：100-111.

[9] Prasannavenkatesan S， Goh M. Multi-objective supplier selection and order allocation under disruption risk[J]. Transportation Research Part E： Logistics and Transportation Review， 2016， 95：124-142.

[10] Neiger D， Rotaru K， Churilov L. Supply chain risk identification with value-focused process engineering [J]. Journal of Operations Management， 2009， 27 （2）： 154-168.

[11] Crockford N. An Introduction to Risk Manageme-nt . Woodhead-Faulkner[R].1986.

[12] Mahajan R B V. The Delphi Method： Techniques and Applicationsby Harold A. Linstone; Murray Turoff [J]. Journal of Marketing Research，1976，13（3）：317-318.

[13] Saaty T L. Modeling unstructured decision problems – the theory of analytical hierarchies[J]. Mathematics & Computers in Simulation，1978， 20（3）：147-158.

[14] 洪志國，李焱，范植华，等.层次分析法中高阶平均随机一致性指标（RI）的计算[J].计算机工程与应用， 2002， 38（12）：45-47.