“离散数学”命题逻辑的教与学研究

王国卿

摘   要：高校“离散数学”命题逻辑与高中数学衔接，是高中数学的延续与深化。针对命题逻辑总体知识结构以及内容细节中的几个关键难点，文章分别从教师和学生的视角出发，详细讲解了如何讲授及理解这些问题的方法。

关键词：命逻辑;逻辑联结词;主范式;重言式

“离散数学”主要研究离散量及离散量之间的关系，是现代数学的重要分支，也是计算机相关专业的基础核心课程。目前，关于在“离散数学”课程中加入实验与实践教学的理念受到了大量教改项目的关注[1-2]。但是，实践与应用是建立在理论知识基础之上的，而命题逻辑是大部分“离散数学”相关教材的第一部分。命题逻辑部分以其概念多、抽象、运算多等特点，让部分学生感觉学起来比较困难。文章通过多年的教学实践，总结出学生在该部分遇到的常见问题，试图从总体知识结构到某些关键难点解答学生的困惑，给相关教师提供一定的参考。

1    命题逻辑的知识结构是一个从具体到抽象的过程

以高等教育出版社出版的屈婉玲等[3]编著的《离散数学》为例说明：第一小节学习命题的定义、逻辑连联结词及命题符号化，涉及的命题全是具体的命题，有具体内容，可以判断真假。类似小学初级阶段数学的学习，学习具体数字的加减乘除运算。第二小节讲命题常项与变项、命题公式、公式的真值表。命题常项就是第一小节涉及的具体的命题，命题变项其实就是命题常项的抽象，或者说是一个映射，定义域是所有具体的命题，值域为0和1。n元命题公式是将0和1构成的长度为n的符号串映射到0或1的映射。在这一小节，命题的具体内容已经不再被关心，关心的重点转移到哪些符号串通过命题公式映射到0（将命题公式映射到0的符号串称作该命题公式的成假赋值），哪些符号串通过命题公式映射到1（将命题公式映射到1的符号串称作该命题公式的成真赋值）。n元的命题公式虽然是千变万化的，有无数多个，但是，它的映射关系只可能有22n种（定义域中有2n次方个元素，值域中有2个元素）。据此，定义n元真值函数，将所有的n元命题公式按等值关系（同真同假的公式为一类，其实就是映射关系相同的为一类）分类，分为22n个等价类，第i个等价类命名为F（n）i-1，等值关系是一个等价关系，因此，这是命题公式的一个划分，n元真值函数集是n元命题公式关于等值关系的商集。这将可以作为后续第二部分理解等价关系与划分的一个重要实例。

2    坚持真值表唯一定义联结词的授课理念

引入逻辑联结词时，为了便于理解与接受，往往用自然语言来描述逻辑联结词的意义。但是，联结词与其相关的自然语义并不是完全相同的，仅抓住这些自然语言，显然学不到逻辑联结词的本质。逻辑联结词本质上是命题逻辑中的运算符号，其运算规则是由真值表唯一确定的。反过来，如果一个命题的真值表与某个逻辑联结词的真值表完全相同，则命题符号化时选用该逻辑联结词。这有助于理解一些较难的逻辑关系。下面举例说明。

例1：（1）王燕学过英语或法语。p：王燕学过英语，q：王燕学过法语。（2）王燕在宿舍或在图书馆。p：王燕在宿舍，q：王燕在图书馆。（3）王燕和小明最多去一人。p：王燕去，q：小明去。问：上述哪个复合命题在符号化时，两个原子命题之间仅用一个析取符号即可。

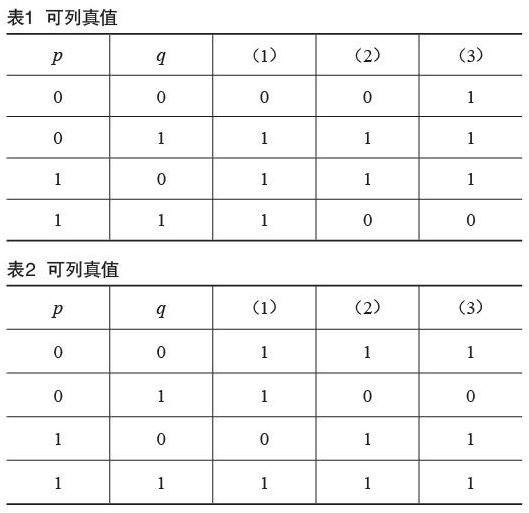
解：可列真值如表1所示。

这样，依据真值表，就可以判断只有（1）可以符号化为;（2）和（3）都不能符号化为。

例2：将下列命题符号化：（1）如果天下雨，我就在家。（2）只有天下雨，我才在家。（3）除非天下雨，否则我不在家。

解：p：天下雨，q：我在家。则可列真值如表2所示。

这样，依据真值表，就可以将上述命题分别符号化为：（1）;（2）;（3）。

3    等值演算法求主范式的技巧

首先，等值演算法基于16组基本等值式与置换规则，求得公式的析取（或合取）范式。其次，查看范式中的简单合取（或析取）式是不是极小项（或极大项），对于不是极小项的，合取1补入缺少的文字（命题变项及其否定），再用分配率展开得到极小项（或极大项）。最后，整理极小项（或极大项）的顺序并将重复出现的极小项（或极大项）合并。

部分同学在补入文字并的计算过程中容易出错，特别是缺少的文字比较多时。据此，通过演算过程带领同学们观察和总结，得到一个小技巧，可以快速由析取范式（合取范式）写出主析取范式（主合取范式）。

观察此题，在简单合取式转化为的两个极小项中，都含有，一个合取r，一个合取，对应的极小项的唯一一组成真赋值刚好是100（对应十进制数4）和101（对应十进制数5）。在r转化的4个极小项中，都含有r，对应的极小项的唯一成真赋值第3个位置固定为1，前两位是0和1的构成的所有排列组合，即001，011，101，111（对应十进制数分别为1，3，5，7）。

综上，对于析取范式中的任何一个简单合取式，将命题变项看成1，将其否定看成0，没有出现的文字可以是0或1，这样组成的所有赋值就是该简单合取式的所有成真赋值，从而可以直接写出与其等值的主析取范式。同理，可以由合取范式直接写出与其等值的主合取范式。对于合取范式中的任何一个简单析取式，将命题变项看成0，将其否定看成1，没有出现的文字可以是0或1，这样组成的所有赋值就是该简单析取式的所有成假赋值，从而可以直接写出与其等值的主合取范式。

4    重言式和矛盾式的主范式的理解

主范式的一个重要应用之一就是可以判断公式的类型。其中的难点是学生对重言式的主合取范式为1、矛盾式的主析取范式为0的理解稍有困难。原因是他们认为重言式的主合取范式没有极大项，按照小学的知识，没有应该就是0。的确，在数论中，0代表什么都没有。但是，这是在命题逻辑中，0和1只是符号，0表示命题为假，1表示命题为真，同样地，F也可以表示假，T也可以表示真。重言式是永真式，所有赋值都是成真赋值，其主合取范式中没有极大项，用1表示。其主析取范式包含了所有极小项，将所有极小项列出。矛盾式是永假式，所有赋值都是成假赋值，其主合取范式包含了所有极大项，将所有极大项列出。其主析取范式中没有极小项，用0表示。

5    如何判断推理有效的问题

推理有效是指由前提合取与结论构成的蕴含式是重言式。这个逻辑思维与我们平时的自然语言“太阳从西边出来了”一致——当前件为假时，说什么都是对的;或者也可以用来表达惊讶、不可能的情感。

由于蕴含式当且仅当前件为真后件为假时才为假，因此，在判定推理是否有效时仅需考虑前件为真的情况。这个思路可以帮助理解推理定律，以及后续一阶逻辑推理和一些由蕴含式定义的概念的理解。推理定律就可以理解为“若前提成立，则结论”;后续二元关系中关系的性质、偏序集中的特殊元素等概念的理解。

6    结语

本文将“离散数学”命题逻辑中的几个难点进行了阐述，希望相关课程教师和学生通过阅读此文能突破命题逻辑中的难点，感受数学严谨之美。后续作者将进一步研究“离散数学”各个部分的重难点，期望能提高学生的学习兴趣，给教师同行们抛砖引玉。

[参考文献]

[1]王海英，蒲新成，陈虹璇，等.基于实验教学的《离散数学》课程改革分析[J].科学咨询（科技·管理），2018（45）：72-73.

[2]王涛，肖巍，徐中宇.基于新工科理念的離散数学课程建设[J].计算机教育，2019（1）：29-30.

[3]屈婉玲，耿素云，张立昂.离散数学[M].2版.北京：高等教育出版社，2004.