黔南水族地区高中学生数学逆商水平调查研究
张 怡,武小鹏
黔南水族地区高中学生数学逆商水平调查研究
张 怡1,2,武小鹏2,3
(1.华东师范大学 数学科学学院,上海 200241;2.黔南民族师范学院 数学统计学院,贵州 黔南 558000;3.华东师范大学 教师教育学院,上海 200062)
数学逆商作为学生学习过程中的一种非智力因素,在学生数学学习中起到很重要的作用.选取黔南水族地区部分高中学生作为样本,以改进后的数学逆商量表为工具,对高中学生数学逆商做了测量.从数学控制、数学归属、数学影响、数学延伸这4个维度出发,分析了数学逆商随年级变化趋势,不同年级学生的性别差异、民族差异,以及逆商各维度、成绩、逆商总和之间的相关性.得出数学逆商具有显著的性别差异和民族差异,数学逆商与数学成绩具有显著的相关性的结论.
数学逆商;民族教育;数学困境;数学教育
1 引言
1.1 研究“背景”“目的”“意义”
《国家中长期教育改革和发展规划纲要(2010—2020年)》指出:“要加强心理健康教育,促进学生身心健康、体魄强健、意志坚强.”[1]现代教育应将培养学生良好的心理素质,提高他们承受挫折的能力摆在教育工作的首位.黔南民族地区相对比较封闭,教育水平比较落后,学生对数学的学习态度、学习动机有很大差异,数学逆商水平千差万别.因此,如何在现代教育体制下,提高少数民族地区高中学生的“逆商”水平,培养高中生应对逆境的能力,便成了当务之急.该研究就高中学生的“数学逆商”为切入点,调查学生的“数学逆商”水平,分析数学逆商与数学成绩、民族、性别、年级等相关变量之间的关系,为民族地区促进学生数学学习的发展提供参考.
1.2 研究问题
(1)不同年级学生数学逆商以及数学逆商各维度的发展变化状况如何?
(2)不同年级学生数学逆商以及数学逆商各维度有无民族、性别差异?
(3)数学逆商及其各维度与数学成绩有怎样的相关性?
2 研究理论
2.1 核心概念界定
2.1.1 逆商
20世纪90年代中期,美国著名学者、职业培训师Stoltz提出逆商的概念.“逆商”全称逆境商数,又称挫折商或逆境商,用来衡量人们面对逆境时的反应方式,即承受挫折、摆脱逆境和超越困难的能力[1].逆商描述的是人们面对逆境的反应方式,也就是将不利局面转化为有利条件的能力.逆商可以分解为4个维度,分别是逆商控制(Control)、逆商归属(Ownership)、逆商延伸(Reach)和逆商忍耐(Endurance),简称为CORE.各维度及其相应的意义阐释如表1所示.

表1 逆商的四因素模型
2.1.2 数学逆商
所谓数学逆商是指一个人对数学学习过程中所遇困难和挫折的应对智力及应对能力,包括4个方面[2].
(1)数学控制,是指个体对数学学习中所遇逆境的控制能力.
(2)数学归属,是指个体认识到数学学习中逆境产生的原因及愿意承担责任、改善后果的能力.
(3)数学影响,是指个体对数学学习中逆境影响范围的评估与觉察能力.
(4)数学延伸,是指数学学习中的逆境对个体的持续影响时间.
2.2 文献综述
逆商最先由Stoltz提出,他认为逆商是个体遇到困难时的反应程度,高逆商者能够很好地处理挫折,选择将压力转化为成功的动力[2].简而言之,逆商反映了一个人承受挫折和克服挫折的能力[3].Stoltz将逆商划分为4个核心维度,分别为控制、归属、延伸和忍耐[4].2000年,Stoltz编制了测量逆商的量表.该量表通过自我评估个人应对逆境情况的类型来测量逆商高低,得分高者在回应挫折时表现良好[5].逆商不仅是职业成功的一项指标,还可以预测和影响人的能力和表现的所有方面[6].研究表明,逆商框架是基于一些理论与心理弹性和脆弱性,包括习得性无助[7]、意志力[8]、内外控倾向[9]和抑郁症的认知模型[10].皇甫倩、王后雄在“积极心理学视角探索学生工作新思路”一文中通过调查分析学生的逆商发现,高中生在逆商的4个维度上分别表现为逆商控制呈下降趋势,逆商归属无明显变化,逆商延伸呈上升趋势,逆商忍耐呈“拐角式”发展;逆商水平的高低与学生学业成绩并无显著相关性.提高高中生的逆商水平,应发挥学校教育的主导作用,构建挫折教育机制;重视家庭教育的辅助作用,拓展逆商培养时空;突出学生在教育中的主体地位,完善自我调控体系[11].
数学逆商是在逆商概念的基础上发展演变出来的.目前对数学逆商的研究还处于初步探索阶段,相关研究较少,典型的有2012年张定强、曹春燕在“初中生数学逆商的调查与分析”一文中将数学逆商分为数学影响、数学控制、数学归因、数学延伸4个维度,通过测量得出中学生的数学逆商与数学成绩显著正相关,数学成绩对数学逆商有显著的影响;数学逆商与数学考试焦虑显著负相关,缓解考试焦虑有助于提升学生的数学逆商[12].2015年曹春燕、张定强发表在《数学教育学报》中题为“民族地区初中生数学逆商的调查与分析”一文中,对甘南藏族自治州藏汉初中生数学逆商做了对比研究,研究发展藏汉地区学生的数学逆商存在显著差异,数学成绩、教师支持等都是影响藏汉学生数学逆商的重要因素,其中父母期望和自我期望等因子对藏汉学生的数学逆商没有显著的影响[13].朱桂凤在“慢教育语境下数学逆商的培养”一文中提到数学逆商教育的培养意义的3个维度:认知心向、数学观念和课程精神.结合慢教育对数学逆商就思维控制力、思维归属力、思维延伸力和思维影响力4个维度给出了培养策略分析[14].国外有研究从性别角度出发,通过调查八年级学生的数学逆商水平,发现男生的数学逆商在数学影响和数学延伸维度表现较好,而女生在数学控制方面优于男生[15].这也进一步说明数学逆商存在性别差异.
逆商作为人的一种重要的非智力因素,在个体成长的道路上起到至关重要的作用.但人们对逆商的重视度不够,尤其是数学逆商的关注度不够.就目前的研究来看,数学逆商的研究还很缺乏,尤其是基于数据的,对学生数学逆商的统计测量还很少.因此,选取高中学生作为研究对象,通过测量学生的数学逆商,研究学生数学逆商与性别、民族、学龄、数学成绩等的关系,进一步了解学生数学逆商整体情况和产生该现象的原因,对深入地了解学生,提高学生数学逆商水平,从而全面培育学生的数学素养起到一定的作用.
2.3 研究框架
研究框架如图1所示.
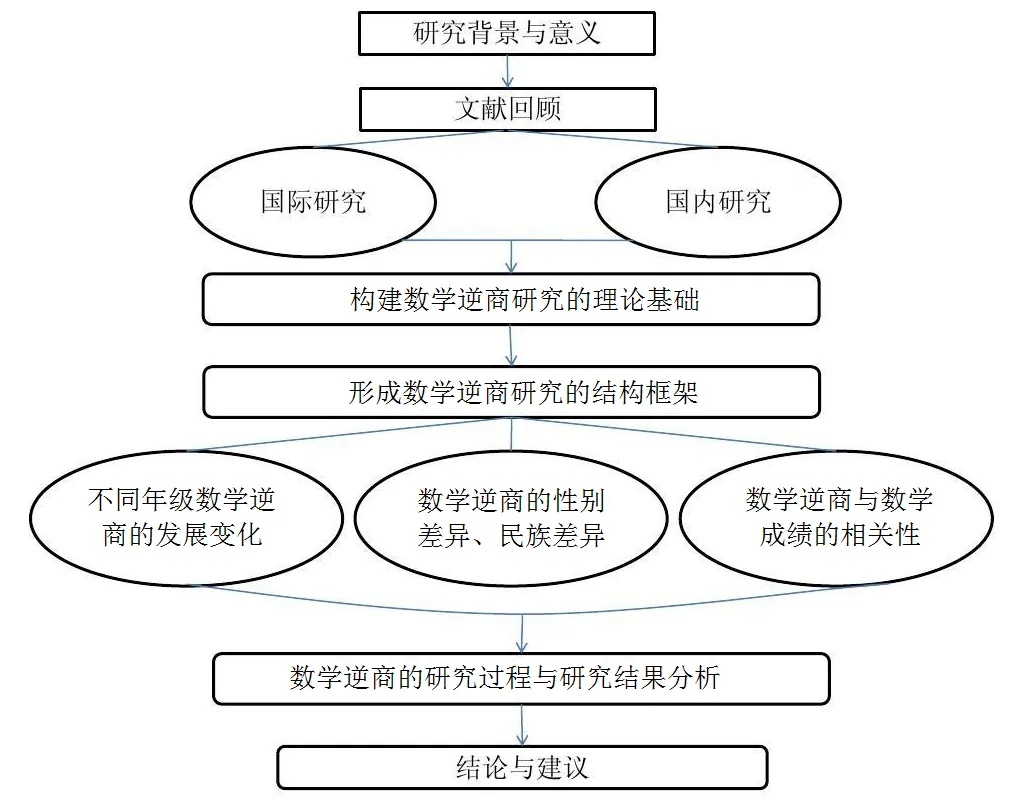
图1 研究框架
3 研究方法
3.1 研究被试
考虑到研究对象的代表性和研究的实际情况,采用分层抽样与随机抽样相结合的方法得到样本.先从黔南水族地区所有高中学校,依据生源质量不同分别选取高、中、低3个学校(生源质量以入学成绩和高考成绩衡量),再从这3类学校中按照不同年级随机抽取样本,已达到调查的全面性.所有样本均选自平行班,不考虑重点班、尖子班的情况.具体信息见表2.研究涉及不同性别、不同年级的高中生,具有可比性,但是由于地域以及样本量等研究条件的限制,研究结果对解释所有民族地区高中生的情况还存在误差,仅在一定程度上有较好的代表性.

表2 抽样调查学生的基本信息
3.2 研究工具
借鉴张定强教授、曹春艳博士开发的“初中生数学逆商量表”[12].考虑到初高中学生在数学逆商水平上的差别,对此量表进行改编,改编主要集中在对涉及到数学内容和数学能力的部分做了进一步深化,使得量表更加符合高中学生的认知水平.例如,将原有的“有时你会抄袭别人的数学作业,你能改善抄袭别人数学作业的这种现象吗?”改为“当你碰到数学难题时,你会在坚持独立思考和放弃探索听教师讲解之间保持良好状态吗?”改编后对量表用Cronbach’s系数(内部一致性系数)分析出数学逆商量表的信度,如表3所示,在可接受范围内.

表3 可靠性统计量
3.3 数据收集与处理
为了避免试题难易程度带来的差异,考试成绩按2016—2017第一学期期中考试成绩统计,该次考试为全州统一考试,试题难易程度适中,避免了无关变量的干扰.调查共发放问卷700份,回收到有效问卷685份.
采用Excel和SPSS20.0进行数据分析,主要用Cronbach’s系数(内部一致性系数)分析出数学逆商量表的信度.在数据分析时,先采用单因素方差分析,得到整体之间是否差异显著,再结合事后多重检验,即LSD法,考察各维度之间的差异显著性.利用检验做了数学成绩与数学逆商差异显著性分析,还做了数学逆商不同维度之间的相关性分析.文中除了差异性分析和相关性分析外,还做了各数学逆商维度随年级的变化趋势分析,不同性别各数学逆商维度随年级的变化趋势等描述性分析等.
4 研究过程与结果
4.1 数学逆商发展变化及其多重分析
学生数学逆商总体测试结果见表4.

表4 学生数学逆商总体测试结果
通过图2可以看出,在高一到高二期间学生的数学逆商水平有一个较大幅度的提升,但高二到高三阶段学生的数学逆商水平,有略微的下降.高一学生数学逆商与高二学生的数学逆商差异显著,说明高一到高二阶段学生的数学逆商提高明显.而高二学生的数学逆商与高三学生的数学逆商,高一学生的数学逆商与高三学生的数学逆商,虽然在图像上有明显变化,但据进一步检验差异不显著,所以高二到高三阶段学生的数学逆商并没有较大幅度的下滑.
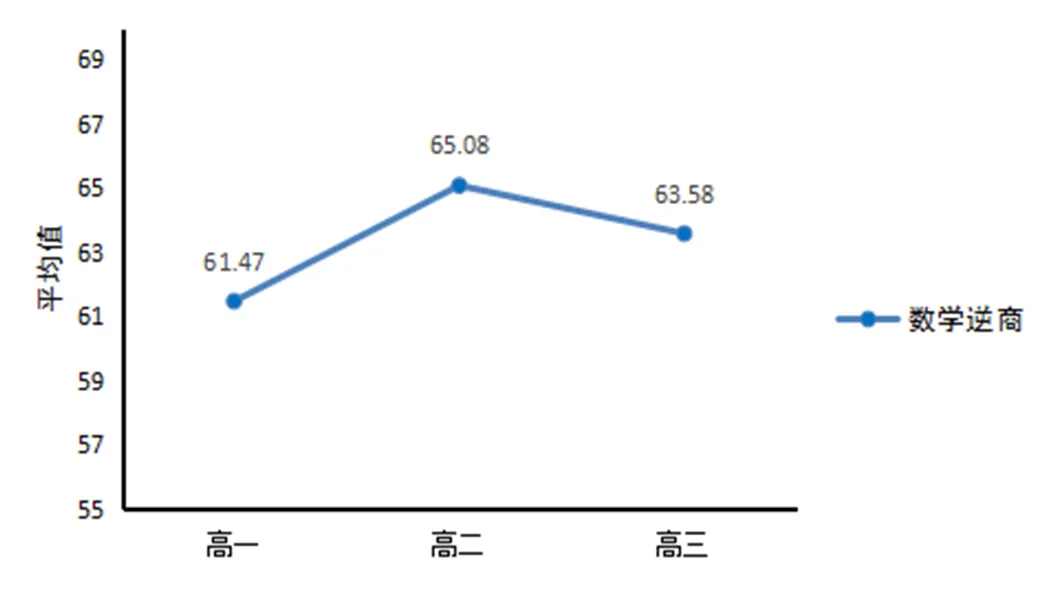
图2 不同年级学生数学逆商发展变化
结合以上4个维度的分析,可以得出,高中学生从高一到高二时期,数学的学习存在着一个思维模式、学习方法、教师适应等方面的转换,学生在这一时期数学逆商的各维度水平都表现出不同程度的上升趋势.说明学生的适应程度对数学逆商有明显的影响[16].到了高二后期到高三阶段,数学学习难度增大,试题由单一的知识点变得更加综合,更加抽象,学生学习数学的难度增加,学生在应对数学困难时显得力不存心,甚至部分数学逆商维度出现了较大幅度下滑.
图3显示了高中男女学生数学逆商随学龄增加的变化情况,从图中可以明显地看出,高中女生数学逆商水平在整个高中阶段表现出下滑的趋势,在高二到高三阶段下滑比较明显.通过分析可知,这种变化是由于高一女生刚进入高中,表现出相对的自信,对数学的学习充满希望,因此,也更加愿意解决数学困难,在数学的学习上更加有信心,数学困难对学生的影响也相对较小.随着数学后续的学习,数学知识点增多,需要学生更强的综合能力,再加上立体几何的引入,还需要学生有较强的空间观念和几何直观能力,高中女生在数学学习的应付上出现了困难,数学逆商水平有所下降.
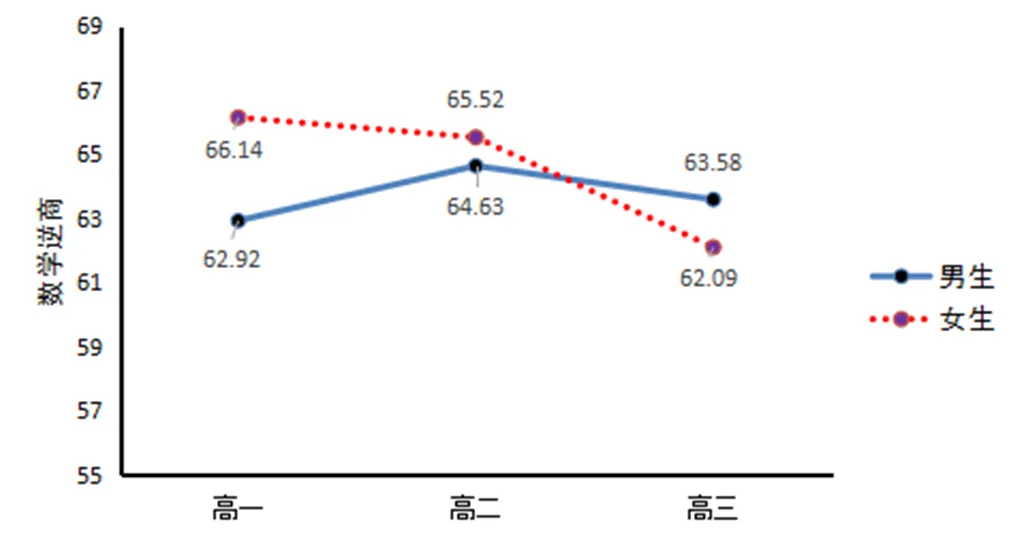
图3 男女生数学逆商发展变化
而高中男生数学逆商水平表现相对平稳,在高一到高二阶段有一个略微的上升,在高二到高三阶段有些许下降.这可以反映出高中男生在面对数学困难时表现相对稳定,还可能与男女生在空间想象能力、逻辑思维能力、抽象概括能力等的性别差异有关[17].
通过上述描述性统计,初步了解了学生数学逆商和数学逆商各维度之间在性别和年级之间存在的差异.但描述性统计由于受到个体分布、试题差异等异质性的特点,很难具有统计学意义.为了进一步明确各年级之间学生的数学逆商是否存在显著差异,需要做出数学逆商的单因素方差分析,分析结果如表5所示.

表5 单因素方差分析
在单因素方差分析中,表示平方和,表示均方,是组间均方与组内均方的比例,表示在相应值下的概率值,是在相应显著水平下的临界值.在统计分析上可以通过的大小来判断组间的差异显著性,通常情况下,当≤0.01有显著差异,>0.05时没有显著差异,介于二者之间时有显著差异.也可通过值来判断差异显著性,当≥时,有显著(或极显著)差异.从表5中可以得出,=0.017<0.05,因此,不同年级的学生数学逆商差异性显著[18].
为了更进一步研究学生的数学逆商是在哪些年级之间存在差异,除了以上整体方差分析外,还做了,即事后多重比较分析,其结果如表6所示.
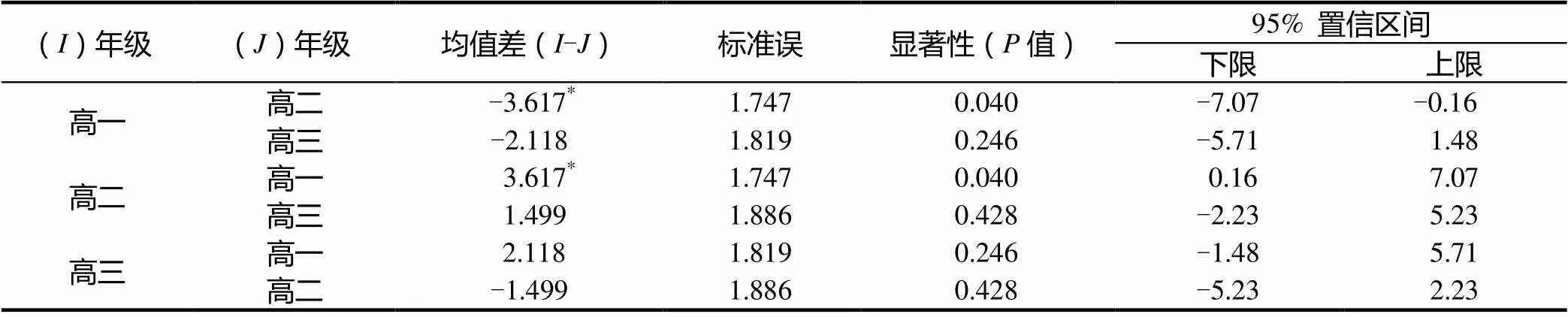
表6 数学逆商分年级多重比较(LSD)
注:*. 均值差的显著性水平为0.05
据表6可以得出,高一年级的数学逆商与高二年级的数学逆商检验结果=0.040<0.05,因此高一年级与高二年级的数学逆商存在显著差异;高一年级的数学逆商与高三年级的数学逆商检验结果=0.246>0.05,因此高一年级与高三年级的数学逆商差异不显著;高二年级的数学逆商与高三年级的数学逆商检验结果=0.428>0.05,因此高二年级与高三年级的数学逆商差异不显著.这一研究结果也和学生数学逆商均值变化规律(如图2)表现一致,进一步说明了数学逆商的变化呈“凸”型这一结论[11].
4.2 数学逆商存在显著的民族差异
为了得到贵州黔南水族地区少数民族(少数民族中87%是水族)和汉族学生在数学逆商水平上是否存在显著的差异,并试图寻找到存在这种差异的原因,并为后期提高黔南水族地区学生的数学逆商提供可靠的依据.先将少数民族学生和汉族学生的数学逆商水平分别进行测量和统计,再通过SPSS软件进行方差分析,得到如表7的结果.

表7 水族和汉族高中学生数学逆商方差分析
据表7可知,黔南水族地区学生的数学逆商和汉族学生存在显著差异.水族学生大多表现为数学逆商水平偏低,学习数学存在较大困难,尤其是数学控制水平的偏低,学生没有学习数学的毅力.主要原因有二:其一,水族地区学校中数学教师水平相对较低(有相当一部分教师是专科或函授本科),在数学学习上没能提供给学生科学合理的学习方法;其二,水族地区对学生的期望较低,学生的学习动力不足.
4.3 数学逆商对数学成绩有较大的影响
数学逆商对数学成绩影响的差异性检验结果如表8所示.

不同数学成绩水平的学生与数学逆商之间总体检验存在着显著的差异,这表明在提高学生的数学逆商时,很有必要按照成绩的不同,分别采取措施提高学生的数学逆商.按照数学逆商的不同维度制定不同的培养策略,例如对于数学成绩较低的学生应该从数学逆商影响维度着手,建立学生对数学学习的自信,克服数学学习过程的焦虑,引导学生对数学带来的困境进行正确合理的分析,做出合理的归因.然而对于成绩水平较高的学生则应该从数学延伸和数学控制入手,让学生能够更好地控制和把握数学逆境带来的范围,更好地进行自我监控,进一步提高数学逆商水平.
4.4 数学逆商不同维度之间存在着不同程度的相关
数学逆商不同维度之间的相关矩阵如表9所示.

表8 数学逆商对数学成绩影响的差异性检验

表9 数学逆商不同维度之间的相关矩阵
注:**. 在置信度(单侧)为0.01时,相关性是显著的.
表9中的数据是按照数学控制、数学归属、数学影响、数学延伸、数学逆商和数学成绩6个因子,采用SPSS统计软件,按照Spearman相关系数计算得到的相关矩阵.依据表9的数据,数学逆商各维度的划分科学合理,因为数学逆商与其数学控制、数学归属、数学影响和数学延伸各维度之间相关性都在置信度为0.01的区间显著,属于高度相关,各维度充分体现了数学逆商的要求.数学逆商与数学成绩Spearman相关系数为0.635,属于高度相关,数学逆商与数学学习成绩之间关系紧密,进一步说明提高学生的数学逆商可以提高学生的成绩,同时为了提高学生的数学逆商,数学成绩也是极其重要的一个因素.学生数学成绩与数学逆商各维度都有较强的相关性.数学逆商各维度之间也有较强的相关性,仅有数学延伸和数学归属相关性不显著.
5 “讨论”“结论”与“启示”
5.1 讨论
(1)对数学逆商研究做了补充.
在前人研究的基础上,对数学逆商的量表依据高中学生的认知特点做了改进,使得测量工具更贴切地反应高中学生处理数学困境的状态.通过测评对测量工具的可靠性做了验证.研究对象选择贵州黔南水族地区,研究内容更加全面,数据处理更加多样,研究部分结果与已有的研究具有一致性.同时还发现数学逆商存在明显的性别差异,尤其要注重高年级女生数学逆商培育;数学逆商存在显著的民族差异;数学逆商与数学成绩显著相关等新结论.
(2)拓宽了逆商研究的视野.
有关逆商的研究目前还很少,并都处于简单的概念介绍和思辨性的经验总结方面.然而,将逆商引入数学学科的研究还少之又少.因此,研究数学逆商对逆商起到了补充作用,同时也对数学逆商研究起到抛砖引玉的作用.拓宽逆商研究视野,关注逆商对学生发展和成长的作用,成为逆商研究的主要目的.
(3)不足与展望.
该研究只做了数学逆商研究水平的调查与分析,样本量较少,代表性有限,仅可以部分解释研究现象.还没能涉及数学逆商影响因素的分析和数学逆商培养策略的研究.今后可以通过聚类分析的方法对数学逆商影响因素进行研究,再利用实验研究法对培养数学逆商的策略进行研究,可以更加全面地服务于教师和学生.
5.2 结论与启示
通过以上数据结果的分析,总结起来可以得到以下3点结论和相应的启示.
(1)数学逆商存在明显的性别差异,尤其要注重高年级女生数学逆商培育.
在图2和表5的分析中,高中男生的数学逆商显著高于女生,学生的数学逆商在高一到高二阶段有较为明显的上升趋势,但高二到高三阶段却出现了下滑趋势.高中女生表现尤为明显.依据这一结论启示教师应在高年级,尤其是高二到高三这一阶段,需注重高中女生数学逆商的培育.引导学生以正常心态和正确的方法面对数学逆境,以恰当的措施控制自己的数学逆商水平,这样也获得自信,顺便提升数学成绩.
(2)数学逆商存在显著的民族差异,需提升水族地区学生民族文化自信.
表7显示了水族(有部分其他少数民族)和汉族学生的数学逆商方差分析结果,依据这一结果可以明确地得出,水族学生的数学逆商要显著低于汉族学生的数学逆商.这种差异体现了他们面对数学逆境的不同态度和处理方式.究其原因,很大程度上是由于少数民族地区,尤其是相对比较偏远的水族地区缺乏民族文化自信.有学者认为,“少数民族文化是这一民族特殊的语言习俗表征,也是这一民族自尊与自信的精神壁垒”[19],要打破这种壁垒,在数学教育中可以将少数民族文化和数学课程、数学教学进行整合,让学生体会到少数民族文化在数学教育中处处存在,并有一定价值,从而增强少数民族学生的文化自信,以提升少数民族学生的数学逆商.
(3)数学逆商与数学成绩显著相关,培养数学逆商是提高数学成绩的抓手.
据表8和表9的统计结果,可以得出数学逆商各维度和数学成绩均存在显著的相关性.也就是说,从数学逆商的每个方面培养学生面对数学逆境的能力,都可以不同程度上提升学生的数学成绩.提高学生的数学逆商,使学生在面对数学问题时,能够提出恰当的解决方案,选择适切的方法,提高解题的效率.在问题解决的过程中,不但培养了学生应对数学难题的智力,同时也降低了学生的挫败感,让学生体会到更多的成就,增强了学生解决问题的自信心.从而,学生对数学的学习产生强烈的内部驱动力,让自主探索、合作学习、交流讨论成为可能[20].教师引导学生面对数学问题,使用恰当的学习方法和多角度全方位思考数学问题的过程,就是学生数学逆商培养的过程.
[1] 保罗斯托茨.逆境商数[M].庄安棋,译.台北:时报文化出版有限公司,2011:16.
[2] PAUL G S. Adversity quotient: Turning obstacles into opportunities [J]. Canadian Manager, 1997 (2): 31, 37-41.
[3] PHOOLKA, SHIVINDER ER, NAVJOT K. Adversity quotient: A new paradigm to explore [J]. Contemporary Business Studies, 2012 (3): 67-78.
[4] STOLTZ P G. Building resilience for uncertain times [J]. Leader to Leader, 2004 (31): 16-20.
[5] WILEY J, STOLTZ P G. The adversity response profile [M]. California: Peak, 2000: 245.
[6] KANJANA KAROON J. Relationship between adversity quotient and self-empowerment of students in schools under the jurisdiction of the office of the basic education commission [J]. International Journal of Learning, 2011 (18): 349-360.
[7] PETERSON C, MAIER S F, SELIGMAN M. Learned helplessness: A theory for the age of personal control [M]. London, UK: Oxford University Press, 1993: 359.
[8] MADDI S R, KOBASA S C. The development of hardiness [M] // MONAT A, LAZARUS R S. Stress and coping: An anthology. 3rd ed. New York: Columbia University Press, 1991: 245-257.
[9] LEFCOURT H M. Durability of impact of the locus of control construct [J]. Psychological Bulletin, 1992 (112): 411-414.
[10] ABRAMSON L Y, ALLOY L B, HOGAN M E, et al. Cognitive vulnerability to depression: Theory and evidence [M] // LEAHY R L, DOWD E T. Clinical advances in cognitive psychotherapy: Theory and application. New York: Springer, 2002: 75-92.
[11] 皇甫倩,王后雄.积极心理学视角探索学生工作新思路[J].教育科学研究,2015(8):48-54.
[12] 曹春艳,张定强.初中生数学逆商的调查与分析——基于数学考试成绩、数学考试焦虑维度[J].数学教育学报,2012,21(4):23-25.
[13] 曹春艳,张定强,丁亥复赛.民族地区初中生数学逆商的调查与分析——以甘南藏族自治州藏汉初中生数学逆商的比较为例[J].数学教育学报,2015,24(2):50-53.
[14] 朱桂凤.慢教育语境下数学逆商的培养[J].教学与管理,2016(3):45-47.
[15] MZ Z A, RISNAWATI, KURNIATI A, et al. Adversity quotient in mathematics learning (quantitative study on students boarding school in Pekanbaru) [J]. International Journal on Emerging Mathematics Education, 2017 (2): 169-176.
[16] 杜宵丰,刘坚.八年级学生“数学兴趣”“数学自我效能感”“学习坚持性”与“数学成就”的关系研究[J].数学教育学报,2017,26(2):29-34.
[17] 周超.八年级学生数学认知水平的性别差异[J].数学教育学报,2011,20(3):59-62.
[18] 王立东,郭衎,孟梦.认知诊断理论在数学教育评价中的应用[J].数学教育学报,2016,25(6):15-19.
[19] 费艳颖,田虹.少数民族文化与现代文化的共生性路径[J].贵州民族研究,2017,38(7):96-99.
[20] 武小鹏,张怡.基于FIAS的高中数学课堂教学比较研究——以2014年全国数学教育研究会两节观摩研讨课为例[J].数学教育学报,2015,24(5):87-91.
The Inverse Research on Mathematics Adversity Quotient Level of the Shui National Students in Qiannan
ZHANG Yi1, 2, WU Xiao-peng2, 3
(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. School of Mathematics and Statistics, Qiannan Normal University for Nationalities, Guizhou Qiannan 558000, China;3. College of Teacher Education, East China Normal University, Shanghai 200062, China)
The Mathematics Adversity Quotient was a kind of non-intellectual factor in the student learning process, which played an important role in the students’ mathematics learning. The author took a sample of some high school students in the national area of Qiannan Shui nationality area, and made a measure of the math inverse quotient of high school students. Analyze the trend of math adversary with the change of grade, the gender difference of different grade students, the national differences, and the correlation between each dimension of adversarial quotient, the scores and the sum of adversaries from mathematics, mathematics, mathematics, mathematics extension of these four dimensions. It was concluded that the inverse quotient of mathematics had significant gender difference and national difference.
mathematics adversity quotient; national education; mathematical difficulties; mathematics education
2019–01–17
2017年黔南民族师范学院校级科研项目——黔南地区初中生数学逆商水平调查研究(qnsy2017030)
张怡(1989—),女,甘肃永昌人,黔南民族师范学院讲师,华东师范大学博士生,主要从事数学课程与教学研究.
G750
A
1004–9894(2019)03–0088–06
张怡,武小鹏.黔南水族地区高中学生数学逆商水平调查研究[J].数学教育学报,2019,28(3):88-93.
[责任编校:周学智、陈汉君]

