基于可靠度理论的尾矿坝失稳概率及敏感性分析

李 涛，刘国栋,2，王 聪

(1.商洛学院城乡规划与建筑工程学院，陕西 商洛 726000；2.长安大学公路学院，陕西 西安 710064)

0 引言

由于尾矿库在成库过程中，受水流的分选作用、矿山机械放矿速度及放矿浓度、成库环境等因素的综合影响，通常会在库区内形成很多个大小不同、粒径差异较大的透镜体结构，其复杂的沉积状态，致使尾矿库溃坝事故频发[1]。而工程勘查通常受外界因素的影响，局部取点进行钻孔取样，测得的土层信息离散性较大，不能正确反映由于局部土层突变而造成的参数变化，这也就使现阶段尾矿库常用计算方法(解析法、模拟法)的计算基础(工程勘查结果)出现了严重问题。

在稳定性上，通常采用极限平衡法或有限元法来计算坝坡的稳定性系数，系数越大，就认为坝体越安全。然而，在实际的生产过程中，由于土体的空间变异性，安全系数并不能完全反映边坡的真实风险水平，稳定系数较高的坝体也有可能比较低的坝体更容易失稳[2]，这也说明现有的计算方法不能完全反映尾矿坝的真实状况。近年来伴随着可靠度理论的发展，基于概率理论对尾矿库进行稳定分析就成为了专家学者研究的焦点[3-5]。

目前常用的可靠度理论有多种。潘建平等[6]利用一次二阶矩法对某尾矿库建立了地震液化分析模型，并对抗液化安全系数与可靠度指标间的关系进行了探讨；胡平安等[7]运用JC法可靠度理论对某坝体进行了正常工况与洪水工况下的稳定性分析，研究表明，概率方法更能反映坝体的真实状态；储昭飞等[8]针对岩土参数变异波动大的特点，利用分位概率设计法(Quantile-Value Method，QVM)对边坡进行了稳定分析，并对抗剪强度的相关参数进行了分项系数与分位概率的标定及误差分析，结果表明，QVM给定的极限状态与目标可靠度之间的误差更小，更符合工程的实际；张浮平等[9]、唐朝晖等[10]、徐根洪等[11]利用蒙特卡罗模拟法(Monte Carlo Simulation)分别对边坡可靠度修正方法、填土边坡及强风化岩石边坡的稳定性进行了概率的可靠性分析，均建议在常规的设计与分析过程中需考虑岩土参数的空间变异性。

基于此，文中利用蒙特卡罗模拟法，考虑土层主要参数的空间变异性，对陕南某尾矿坝进行了基于概率的坝体稳定性分析，旨在为尾矿库后期的运行与管理提供指导性的理论依据。

1 工程概况

该尾矿库位于陕西桑溪镇，属山谷型尾矿库。库内纵深1.1 km，总坝高为59.8 m，设计有效库容98.4×104m3，属Ⅳ等尾矿库。初期坝坝高20 m，坝顶宽度2 m，采用M7.5微风化的花岗石浆砌石挡墙结构，内外侧坡度分别为1∶0.75与1∶0.2，底部设置排水涵管，并在涵管入口处设土工布；堆积坝共十二级，平均坡度为1∶5.26，坡度相对较缓。由于秦岭山区夏日降雨充沛，2012年曾发生过坝体局部破坏，造成了尾矿的泄露，给下游的居民和农田造成了巨大的影响。因此，为了防止此类灾害的再次发生，亟需掌握能够真实反映库区状态的渗流特性与稳定特性。

2 Monte Carloy试验原理

2.1 基本原理

Monte Carlo试验又称统计试验法或随机模拟法，由于计算简单、操作方便等优点，在一些空间变异性较大，且相关参数不易获得的工程中被广泛的应用[12]。作为一种数理统计方法，Monte Carlo试验首先需要建立一个考虑n个风险因素的状态函数；然后，利用数学抽样方法抽取样本，代入状态函数，计算所需的状态值；最后，抽样N次，则可计算出N个状态值，若其中有M次风险，则出现风险事故的概率即为P=M/N。

2.2 尾矿库Monte Carlo试验参数选取

根据尾矿库的地质勘查结果，为了便于计算，先对尾矿库的土层进行了概化处理，将库区内土层划分为尾细砂层与尾粉砂层，并利用Geo-Studio软件的Seep/W与Slope/W模块对洪水工况下的渗透稳定性进行了耦合分析。忽略土层的空间变异性，运用瑞典圆弧法进行计算，其浸润线与潜在的滑移面见图1。

图1 洪水工况下浸润线及潜在滑移面示意图Fig.1 Sketch map of saturation line and potential slip surface under flood condition

由图1可以看出，洪水工况下，浸润线最小埋深为0.92 m，在坡面处已接近出溢。最小安全系数的潜在滑移面在尾细砂层与尾粉砂层穿过，需要考虑各自土层参数的空间变异性，但由工程勘查结果，各层土及初期坝的参数见表1。

表1 土层计算参数

由表1可得，尾细砂层与尾粉砂层仅黏聚力存在差异，且相差不大。因此，近似将两者等同为同一土层，主要土层参数包括容重、内摩擦角、黏聚力、孔隙比、含水量等，则库区的稳定安全系数函数可以表示为：

F=g(x1，x2，x3，…，xn)(1)

上式即为采用Monte Carlo模拟法时的安全系数状态方程，式中：F表示尾矿库稳定安全系数；x1，x2，x3，…，xn为n个具有一定概率分布函数且互不相关的能够反映土层参数的随机变量。参照相关文献[2,12]，将地震作用、地下水位与初期坝的影响设置为定值，主要考虑库区内土层的重度γ，黏聚力c与内摩擦角φ对安全系数F的影响。

(1)试验次数

Monte Carlo模拟是基于大量的数据统计的结果，因此，试验次数直接决定着试验的精度。次数太少，可靠度分析的精度不够；次数太多，则会造成计算机资源的浪费，计算成本太高。因此，Monte Carlo模拟建议的试验次数为：

(2)

式中：ε——期望的可信度(0～100%)；

d——用小数形式表示的符合可信度的标准方差；

m——变量的个数。

假设试验中参数的可信度均为90%，土层γ、c与φ均根据现场勘查测得，且符合正态分布，d值近似取为0.93。因此，Monte Carlo模拟的试验次数为10 174，近似取为10 000次。

(2)抽样次数

将安全系数小于1的概率称为失稳概率。假设失稳概率Pf也服从正态分布，且N次抽样中出现了M次失稳情况，则：

(3)

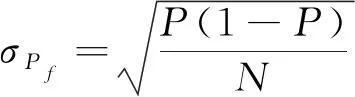
式中：P与σPf——Pf的期望值与标准差。若显著水平取为α，则：

(6)

文中，kα/2——N(0,1)分布的α/2百分位点，α取为0.1。

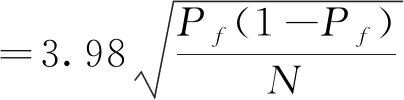
为了提高试验的准确度，减小绝对误差，需要加大模拟次数。因此，一些学者建议Monte Carlo模拟的抽样次数为：

(8)

通常情况下，失稳概率Pf的数值很小，因此，N的数值就比较大，建议近似取N=500～10 000次，可以满足试验精度的要求[13]。

(3)可靠性指标

安全系数反映了边坡的相对稳定，失稳概率反映了边坡的失稳风险水平，两者间没有直接的联系，而可靠性指标则作为一种考虑不确定性因素的安全系数标准化指标而被广泛应用。

若已知了Monte Carlo模拟参数的概率分布函数，则可靠性指标β[14]可表示为：

(9)

式中：μ和σ——公式(1)的数学期望与标准差，分别由下式进行计算：

(10)

式中：n——抽样总次数；

Fi——每次抽样的失稳概率。

3 概率分析

将尾细砂与尾粉砂视作同一土层，黏聚力取两者平均值，以库区砂层表示，服从正态分布。利用正态概率密度函数(图2)的特性：任意点与期望点及其在X轴上投影所围成的面积仅取决于标准值与平均值的差值。因此，经过计算，当x的取值在±1σ之间时，所围面积为68.26%，也即其概率值为68.26%；当x的取值在±5σ之间时，其概率值就几乎为100%。因此，Slope/W就默认标准差均为±5σ。以天然重度为例，当μ=19 kN/m3，σ=0.6时，其波动的区间就为：16～22 kN/m3。Monte Carlo模拟的土层参数值见表2所示，天然重度的概率密度与概率分布函数见图2与图3所示。

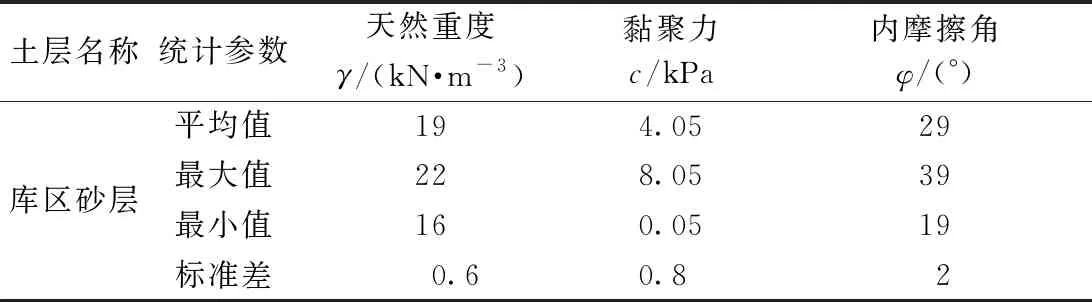
表2 Monte Carlo模拟试验参数

图2 天然重度概率密度函数Fig.2 Probability density function of natural unit weight

图3 天然重度概率分布函数Fig.3 Probability distribution function of natural unit weight

表3为不同的抽样方式下， Monte Carlo试验的统计结果表。但整体来说，抽样方式的不同，对平均安全系数μ的影响较小，对失稳概率σ、Pf及β的影响较大，而每个条块都抽样与仅抽样一次，提供了相应统计结果的范围。不管采用哪种抽样方式，σ、Pf与β的范围分别为：0.042～0.122，0.011～9.489，3.619～1.238。也可以看出，当采用间隔30 m与60 m二种不同的抽样方式时，μ是一样的，但后者的失稳概率却是前者的2.908倍，因此，也验证了将安全系数作为评判尾矿坝体是否稳定的标准是不合适的。

表3 Monte Carlo试验统计结果表(洪水水位)

不管采用哪种抽样方式，安全系数密度函数与分布函数的形状是相似的，平均安全系数相差也不大。图4与图5为仅抽样一次时的Monte Carlo试验概率统计函数。由图4可以看出，安全系数依旧服从正态分布。由图5则可以很方便的计算出所需计算点处的失稳概率与超越概率，例如，A点的超越概率为50%，B点的失效概率为9.489%。

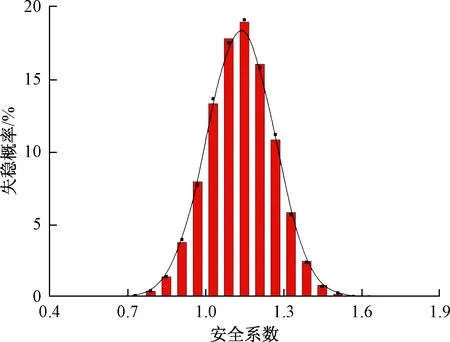
图4 安全系数概率密度函数(仅抽样一次)Fig.4 Probability density function of safety factor (Sampling only once)

图5 安全系数概率分布函数(仅抽样一次)Fig.5 Probability distribution function of safety factor (Sampling only once)

图6为可靠度指标与失稳概率的关系曲线，由图可以看出，两者是一一对应的。经公式拟合，可得：

Pf=-0.89+36.48×0.36β(11)

图6 可靠度指标与失稳概率的关系曲线Fig.6 Relationship between reliability index and instability probability

4 敏感性分析

利用概率分析，我们可以分析出尾矿库在多因素不确定变量的影响下，发生失稳破坏的概率，但是如果想要知道各变量对失稳概率的影响程度，就需要进行敏感性分析，也即需要将随机变量按照均匀概率分布函数进行选取。

采用表2的试验统计参数，文中对库区内砂层的主要土层参数进行了Monte Carlo敏感性分析。为了便于对比分析，所有指标均进行了归一化处理，即x轴的敏感性范围为0～1(图7)。

图7 Monte Carlo敏感性分析曲线Fig.7 Monte Carlo sensitivity analysis curve

由图7可以看出，对于该库区砂层，各项参数对安全系数的影响敏感性为：黏聚力>内摩擦角>砂层容重。在土层参数中，黏聚力起主要控制作用，而且对安全系数的变化影响程度要远远大于内摩擦角与容量，使安全系数的波动范围处于0.905～1.394之间，而内摩擦角与容重的变化范围相对较小，分别处于0.975～1.281与1.006～1.298。当库区砂层容重在16～22 kN/m3的范围内变动时，安全系数的失效概率为0，也即容重的变化不会使尾矿库发生失稳现象。因此，今后尾矿库在运行的过程中，要尽量避免土层发生过大的扰动，以避免黏聚力发生太大波动，影响尾矿库的安全稳定性。

Monte Carlo模拟利用概率分析，能够考虑空间变异特性及不确定因素的影响，不考虑问题的维数，也不必对问题进行精细化与离散化建模，因这些优点而被广泛的应用。但由于Monte Carlo模拟需要将确定性问题转化为随机性问题，且需要试验和抽样较多的次数，方能得到相对可靠的结果。因此，相关参数的标准差与试验和抽样次数的确定，就变得至关重要。如何在考虑参数标准差的基础上，在相对较少的试验和抽样次数上(节约资源)得到具有一定可靠度的抽样结果，还需要在今后继续研究。

5 结论

使用工程勘查结果对尾矿库渗流稳定性进行定量分析，没有考虑库区土层的空间变异性，简单的使用安全系数作为评判唯一标准就带有很强的主观性，还可能出现安全系数与工程实际不符的现象。本文运用Monte-Carlo概率分析与敏感性分析，对砭家沟尾矿库洪水工况下的渗流稳定性进行了分析，主要得出了以下结论：

(1)抽样方式的不同，没有导致平均安全系数的变化，但是却使失稳概率和可靠性指标发生了大幅波动。随着抽样次数的减少，失稳概率逐渐增大，可靠性指标逐渐降低，且两者存在一一对应关系。仅抽样一次到每个条块都抽样，提供了失稳概率及可靠性指标的范围分别为：9.489～0.011与3.619～1.238。Monte-Carlo概率分析也验证了仅靠安全系数来衡量坝体是否失稳是不可取的。

(2)经过对库区砂层参数的敏感性分析，可以得到各项参数对尾矿库安全系数的影响敏感性为：砂层黏聚力>内摩擦角>容重。经过对敏感性曲线的分析，可以看出，砭家沟尾矿库库区砂层容重的变化，不会产生失稳现象；黏聚力对库区安全性的影响最为敏感，使安全系数的波动范围最大，处于0.905～1.394。今后在使用的过程，还需要注意使土层不发生过大的扰动，避免黏聚力发生波动。