Weibull分布引进故障的软件可靠性增长模型*

王金勇, 张 策, 米晓萍, 郭新峰, 李济洪

1(山西大学 软件学院,山西 太原 030006)

2(哈尔滨工业大学(威海) 计算机科学与技术学院,山东 威海 264209)

软件测试和调试是一个复杂的过程,其中,测试者和调试者的能力和技术对软件故障的检测和排错有着重要影响.当一个故障被检测出来时,调试人员需要用相关的知识去考虑怎样完全去除和修复故障,而且不要引入新的故障.但是,调试过程会被许多因素影响,例如调试者的技术、调试用的工具、调试环境和调试人员在调试过程中的心理变化等.这些因素都会影响调试人员在去除故障时是否会引入新的故障.人们一般称在软件调试过程中,当检测出的故障被去除时,引进新的故障现象为不完美调试.

在过去的40年里,研究者对不完美调试现象进行相关的研究,而且也提出了许多不完美调试的软件可靠性增长模型.由于不完美调试情况的复杂性,人们一般把不完美调试过程看做是具有不确定性的随机过程.另外,在实际的软件测试过程中,软件检测出故障的数量不一定和故障去除的故障数量相等,例如,去除一个已检测出的故障可能会引入新的故障或者原来的故障没有被完全去除.也就是说,在不完美调试过程中,故障总个数可能会增加.G-O[1]首先提出了不完美调试的概念,Obha等人[2]在 G-O模型的基础上提出了故障引进的不完美调试软件可靠性模型.Kapur等人[3]提出了故障检测率随测试时间下降的不完美调试软件可靠性增长模型.Pham等人[4,5]通过考虑线性引进故障现象和合并多失效类型的故障生成过程,提出了相应的不完美调试的软件可靠性模型.Zhang等人[6]和Kapur等人[7]分别就软件调试过程中故障引进的不同形式提出了相应的软件可靠性模型.另外,Kapur等人[8]通过研究故障检测和故障去除之间的不同分布情况,提出了两个一般的框架(framework),并得出了几个具有NHPP类的不完美调试的软件可靠性增长模型.Wang等人[9-11]通过对故障引进现象的研究,分别提出了故障引进非线性变化和故障引进了先增后减的不完美调试的软件可靠性增长模型.另外,王金勇等人[12]还提出了在软件测试过程中,故障引进率不规则变化的完美调试的软件可靠性增长模型.谢景燕等人[13]通过对不完美调试过程中引进故障和不完全去除故障的研究,提出了故障排错率随测试时间变化的不完美调试的软件可靠性模型.

虽然上面提到的关于不完美调试软件可靠性模型在实际测试过程中能够有效地评估软件可靠性和预测软件中存在的剩余故障的数量,但是没有哪一种模型能够应用到软件测试的所有环境下[14].因此,还需要对软件调试过程中故障引进现象进行深入研究.实际上,故障引进不但可能是线性[4]、指数分布[15,16]或者与故障排错的数量成正比[7],而且还可能是更复杂的变化,可能受到调试过程中的环境、工具以及调试者的能力和技术等影响.因此,故障引进在软件调试过程中是一个需要重点考虑的因素.

在本文中,我们用Weibull分布来模型化故障引进过程.Weibull分布有许多优点:第1,与指数分布具有无记忆性相比,它具有记忆性;第2,它可以模型化多种故障数据集,例如模型化左倾(left-skewed)、右倾(right-skewed)或者对称数据(symmetric data);第3,当形状参数变化时,它可以有不同的形状;第4,它可以模型化故障引进强度函数随时间的变化,例如故障引进的强调函数随时间具有先增后减的变化或者下降的变化等.因此,考虑在实际的软件调试过程中,用Weibull分布来模型化故障引进随测试时间变化的过程,是一种有效的和可行的方法.

另外,用Weibull分布来模型化故障引进现象,与其他方法相比还有其他优势.例如,用Weibull分布模型化故障引进的现象,可以考虑故障引进率随测试时间先增后减和逐渐减少的变化趋势.但是其他一般只能模型化故障引进的一种变化.因此,用其他方法建立的软件可靠性模型对软件测试和调试的环境适应性具有一定的限制.而用Weibull模型化故障引进过程建立的软件可靠性模型则能更好地适应软件测试和调试的复杂变化.本文中的实验结果也证明了提出的模型和其他不完美调试的软件可靠性模型相比,具有更准确的故障拟合和故障预测性能,而且提出的模型能更好地适应不同软件测试和调试环境下.

1 故障引进服从Weibull分布的原因和表示

(1) 缩略语

· NHPP:非齐次泊松过程;

· SRGM:软件可靠性增长模型;

· MLE:最大似然估计;

· MVF:均值函数;

· SSE:误差平方和;

· AIC:Akaike 信息标注.

(2) 符号说明

·a:期望引进故障的总数量;

·b:故障检测率;

·c:故障检测率的上边界;

·d:形状参数;

·p:故障去除效率;

·α:率参数;

·β:拐点因子;

·r:常量故障检测率;

·α1:比例参数;

·β1:形状参数;

·n:实际观测到的故障数量;

·C:期望检测出最初故障总数量;

·N(t):随机变量,即,表示到t时刻为止,检测出故障的数量;

·a(t):故障内容(总数)函数;

·b(t):故障检测率函数;

·oti:表示到ti时刻为止,实际观测到故障的数量;

·m(ti):均值函数,表示到ti时刻为止,期望检测出故障的数量.

1.1 Weibull分布相关概念和表示方法

Weibull分布是一个连续的概率分布,以瑞典工程师、数学家Waloddi Weibull的名字命名.

(1) Weibull 概率密度函数可以表示为

其中,f(x;λ,k)是概率密度函数,x是随机变量,λ是比例参数,k是形状参数.

Weibull概率密度函数有下列特点.

① 当k<1时,Weibull概率密度函数曲线在随机变量x逐渐增加时,有急剧下降的趋势;

② 当k=1时,Weibull概率密度函数曲线在随机变量x逐渐增加时,有逐渐缓慢下降的趋势;

③ 当k>1时,Weibull概率密度函数曲线在随机变量x逐渐增加时,有先增后降的趋势.

从图1能够清晰地看到这种变化.考虑到Weibull概率密度函数的这些特点,可以用来模拟故障引进率先增后减和逐渐下降的过程.

(2) Weibull累计分布函数可以表示为

其中,F(x;λ,k)为Weibull累计分布函数.

Weibull累计分布函数有下列特点.

① 当k=1时,它为指数分布(exponential distribution);

② 当k=2,λ= 2λ时,它为瑞利分布(rayleigh distribution).

从图 2能够清晰地看到 Weibull累计分布函数在随机变量x逐渐增加时发生的相应变化.考虑到 Weibull累计分布函数的特点,因此可以用来模拟故障引进过程.

1.2 故障引进服从Weibull分布的原因

为了简化已建立不完美调试软件可靠性增长模型的复杂性,一般都是假设软件调试过程中,故障引入率或者为常数,或者故障引入服从指数分布.但在实际软件调试中,故障引入率有可能不为常数,故障引入可能会受到许多因素的影响,例如调试者的技术和调试的环境等.软件测试是一个复杂的过程,受到很多外部或内部的因素的影响,不可能建立一种模型把所有的故障引入的因素都考虑进去.因此,综合考虑故障引入的变化,在实际的软件调试过程中更有一定的实际意义.

另一方面,Weibull分布有许多优点,例如可以模拟多种其他分布函数形状,通过Weibull参数的变化,有效地表示实际软件调试过程中故障引入的复杂变化.所以,用Weibull分布函数来建立不完美调试条件下的软件可靠性模型还是有一定的实际意义.并且随着人们对软件可靠性建模的不断深入了解和认识,综合考虑故障引入条件,并通过Weibull分布函数来建立相应的不完美软件可靠性模型,则更符合软件可靠性调试的实际情况.

在实际软件调试过程中,故障引入会发生复杂变化,考虑用其他分布函数来模拟故障引入的情况,不能完全反映故障引入的随机变化.虽然有的不完美调试软件可靠性增长模型考虑了指数分布的故障引入情况,但是由于指数分布具有无记忆性,即P(s+t/t)=P(t),和发生的时间s无关.这一性质对于故障引入情况来说,是不符合故障引入的实际变化.也就是说,在实际的调试过程中,故障引入发生的概率会随着测试时间逐渐变小,而不会与以前的故障引入发生概率相等.由于Weibull分布函数没有无记忆性的性质,因此,用Weibull分布函数来模拟故障引入的过程会更有效地反映实际的软件调试过程中故障引入情况.另外,它还可以模拟故障引进率随测试时间下降、不变和先增后减的变化.

因此,考虑用Weibull分布来模拟故障引进过程是可行、合理的.本文的实验结果也证明:用Weibull分布来模拟故障引进随测试时间变化的情况,是建立高质量的软件可靠性增长模型最好的方法之一.

1.3 用Weibull分布模拟故障引进过程

从以上的分析可以得出,故障引进情况可以用Weibull分布函数来表示.因此,故障内容(总数)函数可以被表示为

其中,a表示最终期望引进故障的总数量,F(t)是故障引进的分布函数,C是最初期望的软件内存在的故障数量,a(t)是故障内容(总数)函数.

故障引进强度函数可以表示为

假设故障内容(总数)函数服从Weibull分布,即故障内容(总数)函数a(t)与故障引进强度函数可分别表示为

其中,α为率参数,d为形状参数.

考虑到故障引进过程主要是考察故障引进率随测试时间发生变化的情况,因此,故障引进强度函数可以改写为以下形式:

其中,h(t)表示故障引进率函数;[a+C-a(t)]表示到t时刻为止,期望剩余故障引进故障的数量.

在公式(7)中,[a+C-a(t)]是一个随时间增长而非增长的函数.因此,故障引进强度函数的变化趋势是由故障引进率的变化决定的.例如在公式(8)中:当d=1时,公式(7)意味着在(t,t+Δt)时间内引进故障的数量和剩余故障引进故障的数量成正比,即故障引进率为常数;当d<1时,故障引进率函数h(t)随测试时间逐渐下降;当d>1时,故障引进率函数h(t)随测试时间有逐渐增加的变化趋势.

2 提出的不完美调试模型的建立

2.1 提出模型的基本假设

提出模型的假设条件如下.

① 软件失效和故障去除过程遵循非齐次泊松过程(NHPP);

② 软件失效发生是随机发生的,发生的原因是由软件中剩余故障造成的;

③ 每次检测到一个软件故障,立即被去除,并且可能引进新的故障;

④ 故障内容(总数)函数服从Weibull分布.

从上面的假设可以看出,假设③和假设④捕获了在软件调试过程中,故障引进过程所表现出的变化.

2.2 提出模型建立过程

一般来说,基于 NHPP的模型都是假设软件失效是随机发生的,在(t,t+Δt)时间内,期望软件发生失效的数量和期望软件剩余故障发生的数量成正比[17].这意味着软件故障检测率为常量,它可以用以下微分方程来表示:

其中,m(t)表示均值函数,b(t)表示故障检测率,a(t)表示故障内容(总数)函数.

基于假设③和假设④,故障内容(总数)函数可以表示为

这里的a为期望最终引进故障的总的数量,α为率参数,d为形状参数,C为期望最初软件中存在的故障的数量.当t=0,a(0)=C;当t→∞,a(∞)=a+C.公式(10)两边求导,得:

从公式(11)可以得到:

① 当d≤1时,故障引进随测试时间逐渐减少;

② 当d>1时,故障引进随测试时间有先增后减的变化.

因此,从公式(11)可以得出,故障引进随测试时间发生变化的情况.

当b(t)=b,把公式(10)带入公式(9)可得到:

因为公式(12)是一个复杂的微分方程,可以得到近似解为

当k=5时:

公式(13)就是提出的模型的表达式,公式(14)是所用到的提出模型的表达式.从公式(13)和公式(14)可以得到:当t=0,m(0)=0;当t→∞,m(∞)=a+C.

2.3 提出的模型证明

公式(15)两边积分得:

当b(t)=b和a(t)=a[1-exp(-αtd)]+C,公式(18)可以转换成以下形式:

因为麦克劳林公式为

所以可以用公式(20)简化公式(19),可得:

其中,C1为一个常数.当t=0,m(0)=0时,把它代入公式(24),可得:

取k=5时,公式(25)可得:

3 模拟实验

为了充分、有效地评估提出模型的拟合和预测性能,本节给出模型比较标准和模型参数的估计方法.我们还用两个故障数据集进行相应的仿真实验和模型的置信区间分析.表1列出了在本文中进行比较的所有模型.

Table 1 Summary of some SRGMs and their m(t)表1 软件可靠性增长模型和m(t)

3.1 模型的性能比较标准

除了以前使用过的AIC[12]模型评价标准外,在这里还给出了其他模型比较评价标准.

(1) 误差平方和

其中,n表示故障数据集的样本大小.SSE值越小,说明模型的性能越好.

(2) Bias评价标准

Bias表示实际观察到故障值和估计的故障值之差的绝对值之和的平均数,它的定义可以表示为

其中,m(ti)表示到ti时刻为止,期望估计检测出故障的数量;oti表示实际观察到故障发生的数量;n为故障数据集样本大小.Bias值越小,说明模型的性能越好.

(3) Variance评价标准

Variance表示估计偏差的标准差[21],它可以表示为

Variance值越小,说明模型的性能越好.

(4) RMSPE(root mean square prediction error)评价标准

RMSPE表示模型预测出故障发生数量偏差性[21],它可以定义为

RMSPE值越小,说明模型的性能越好.

3.2 故障数据集

第 1组故障数据集来自文献[22],总共用时 22天,86个软件故障被检测出来.第 2组故障数据集来自文献[23],它是一个支持航空飞行器(space shuttle flights)的软件系统,测试用时38周,231个软件故障被检测出来;另外,这个故障数据集包括重要故障(critical errors)、主要故障(major errors)和次要故障(minor errors).第3组故障数据集和第4组故障数据集是Musa[24]收集和整理的,这两个故障数据集是实际测试(real-world)中得到的,它们的系统代码分别为4和27,被研究者广泛用于新建的软件可靠性模型性能评测中.第3组故障数据集包括测试用时72天,54个故障被检测出来.第4组故障数据集包括测试用时79天,41个故障被检测出来.

为了充分地验证和评估提出模型的拟合和预测能力,我们把故障数据集 1和故障数据集 2划分为 63%和80%的子故障数据集.也就是说,分别用63%和80%的故障数据集来拟合和估计模型的参数,剩余37%和20%的故障数据集用来预测和评估模型的性能.另外,我们把故障数据集3和故障数据集4划分为60%和80%的子故障数据集.即,分别用60%和80%的故障数据集来拟合和估计模型的参数,剩余40%和20%的故障数据集用来预测和评估模型的性能.

3.3 模型的参数估计方法

本文用的参数估计方法是用最大似然估计方法,它可以表示为

为了方便计算,两边取对数为通过对l取导数,联立解方程组,则提出模型的参数(a,b,d,α和C)可以被估计出来(a*,b*,d*,α*和C*):

3.4 模型的性能比较

1) 数据集1(DS1)

从表2可以看到,在用63%的故障数据集时,与其他模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是124.0;其次是DSS模型,为241.6;最差是P-Z模型,为851.6;

· 有关Biaspredict的值方面,提出模型的Biaspredict值最小,仅为 3.5;其次为 DSS模型,为 5.5;最差为 ISS模型和P-Z模型,为10.1;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为 5.1;其次为 G-O模型、Yamada不完美调试模型-1、Yamada不完美调试模型-2、Zhang-Teng Pham模型、Kapur模型-1和Kapur模型-2,都是6.5;最差为ISS模型和P-Z模型,都为21.7;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为6.2;其次为G-O模型、Yamada不完美调试模型-1、Yamada不完美调试模型-2、Zhang-Teng Pham模型、Kapur模型-1和kapur模型-2,都为8.9;最差是ISS模型和P-Z模型,都为23.9;

· 有关AIC值方面,提出模型的AIC值也是最小,仅为76.1;其次为DSS模型,是76.2;最差是Zhang-Teng Pham模型,为93.1.虽然DSS模型拟合得很好,它的AIC值和提出模型的AIC值很接近,但是DSS模型的SSEpredict,Biaspredict,Variancpredicte和RMSPEpredict的值却远大于提出模型相应的值.因此,提出的模型在同其他的软件可靠性模型相比,有更好的故障拟合效果和预测能力.

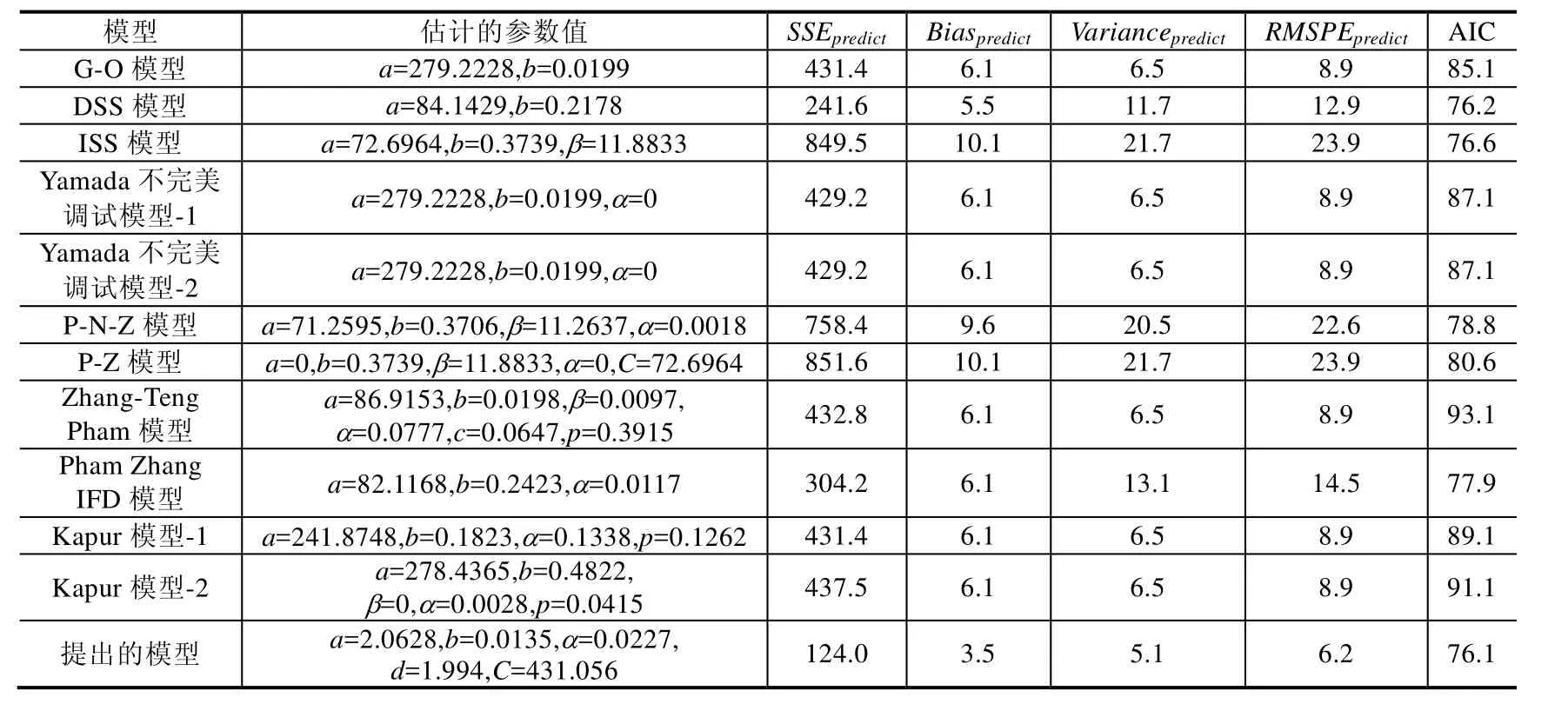
Table 2 Comparison results of different SRGMs for the first data set (63% of DS1)表2 第1组数据集上不同软件可靠增长模型的比较结果(63%故障数据)

图3(a)给出了提出模型使用故障数据集 1的63%进行故障拟合和预测的95%的置信区间,我们也能看出:提出的模型很好地拟合故障数据,并准确地预测了在实际的软件测试当中,软件故障发生的数量.另外,在图3(a)中,实际观察到的故障数量较好地落在提出模型的 95%上下界中.同时我们也能看到,提出模型有很好的拟合效果和准确的软件故障预测行为.

图3(b)给出了提出模型使用故障数据集1的80%进行故障拟合和预测的95%的置信区间,我们也能看出:提出的模型很好地拟合故障数据,并精准地预测在实际的软件测试当中,软件故障发生的数量.另外,在图 3(b)中,实际观察到的故障数量很好地落在提出模型的 95%上下界中.同时我们也能看到,提出模型有很好的拟合效果和精确地预测软件故障发生.

从图3(a)和图 3(b)可以看出:提出的模型不论是用63%的故障数据,还是用80%的故障数据时,都能很好地拟合软件故障数据和准确地预测软件故障发生.因此,可以合理地得出,提出的模型有很好的拟合能力和软件故障预测能力.

图3(c)给出了提出模型使用故障数据集 2的63%进行故障拟合和预测的95%的置信区间,我们能看到:提出的模型很好地拟合故障数据,并较好地预测软件发生故障的行为.另外,在图3(c)中,实际观察到的故障数量很好地落在提出模型的 95%上下界中.同时我们也能看到,提出模型有很好的拟合效果和准确地预测软件故障发生行为.

图3(d)给出提出模型使用故障数据集2的80%进行故障拟合和预测的95%的置信区间,我们也能看到:提出的模型很好地拟合故障数据,并精确地预测软件故障发生的数量.另外,在图3(d)中,实际观察到的故障数量很好地落在提出模型的 95%上下界中.同时我们也能看到,提出模型有很好的拟合效果和精确地预测软件故障发生数量.

从图3(c)和图 3(d)可以看出:提出的模型不论是用63%的故障数据,还是用80%的故障数据时,提出的模型很好地拟合故障数据,并且准确地预测软件发生故障的行为.因此,在软件故障拟合和软件故障预测方面,提出的模型都有很好性能.

从表3可以看到,在用80%的故障数据集时,与其他模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是 2.9;其次是 DSS模型,为 3.6;最差是G-O模型、Yamada不完美调试模型-1和Kapur模型-1,为49.5;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为0.8;其次为DSS模型和Pham Zhang IFD模型,为0.9;最差为G-O模型、Yamada不完美调试模型-1和Kapur模型-1模型,为2.9;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为1.7;其次为DSS模型,是2.0;最差为ISS模型、P-N-Z模型和P-Z模型,都为5.4;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为1.9;其次为DSS模型,为2.1;最差是ISS模型和P-Z模型,都为5.9;

· 有关AIC值方面,提出模型的AIC值也是最小,仅为95.7;其次为DSS模型,是96.2;最差是Zhang-Teng

Pham模型,为115.1.虽然DSS模型拟合得很好,它的AIC值和提出模型的AIC值很接近,但是DSS模型的SSEpredict,Biaspredict,Variancepredict和RMSPEpredict的值却大于提出模型相应的值.因此,提出的模型在同其他的软件可靠性模型相比,有更好的故障拟合能力和预测软件发生故障的能力.

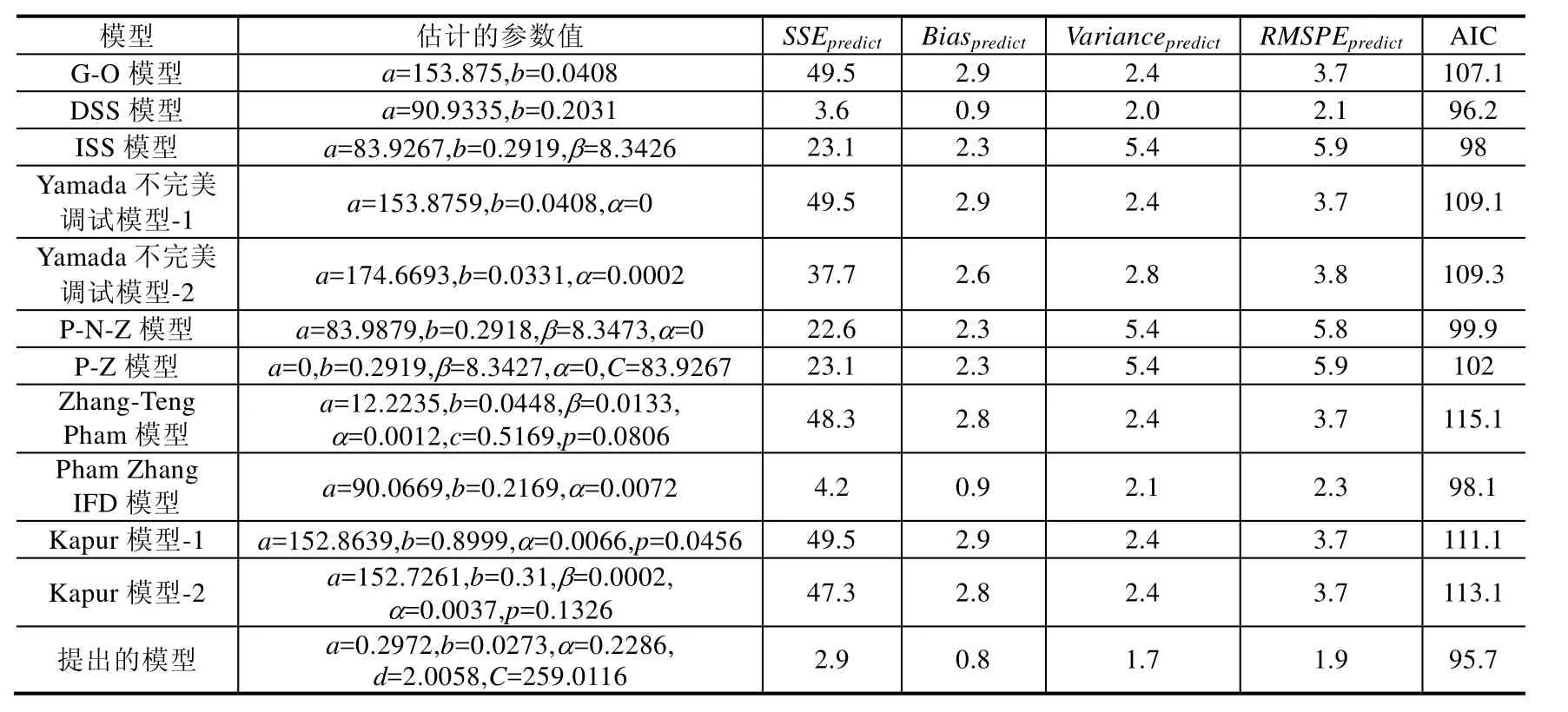
Table 3 Comparison results of different SRGMs for the first data set (80% of DS1)表3 第1组数据集上不同软件可靠增长模型的比较结果(80%故障数据)

2) 数据集2(DS2)

从表4可以看到,在用63%的故障数据集时,与其他软件可靠性模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是848.6;其次是Kapur模型-1,为1328.5;最差是Yamada不完美调试模型-1,为38647.3;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为7.2;其次为G-O模型、ISS模型、P-Z模型、Zhang-Teng Pham模型、kapur模型-1和kapur模型-2,都为9.0;最差为Yamada不完美调试模型-1,为45.7;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为4.1;Zhang-Teng Pham模型也为4.1;其次为G-O模型、ISS模型、Yamada不完美调试模型-2、P-Z模型、Kapur模型-1和Kapur模型-2,都是4.3;最差为DSS模型和Pham Zhang IFD模型,都为31.5;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为8.4;其次为Zhang-Teng Pham,为9.9;最差是Yamada不完美调试模型-1,为53.0;

· 有关AIC值方面,提出模型的AIC值也是最小,仅为116.9;其次为Yamada不完美调试模型-1,是117.1;最差是Pham Zhang IFD模型,为175.1.虽然Yamada不完美调试模型-1拟合得很好,它的AIC值和提出模型的 AIC值很接近,但是 Yamada不完美调试模型-1的SSEpredict,Biaspredict,Variancpredicte和RMSPEpredict的值却远远大于提出模型相应的值.因此,提出的模型与其他的软件可靠性模型相比,有更好的拟合故障数据的能力和更准确地预测软件中发生故障的数量的能力.

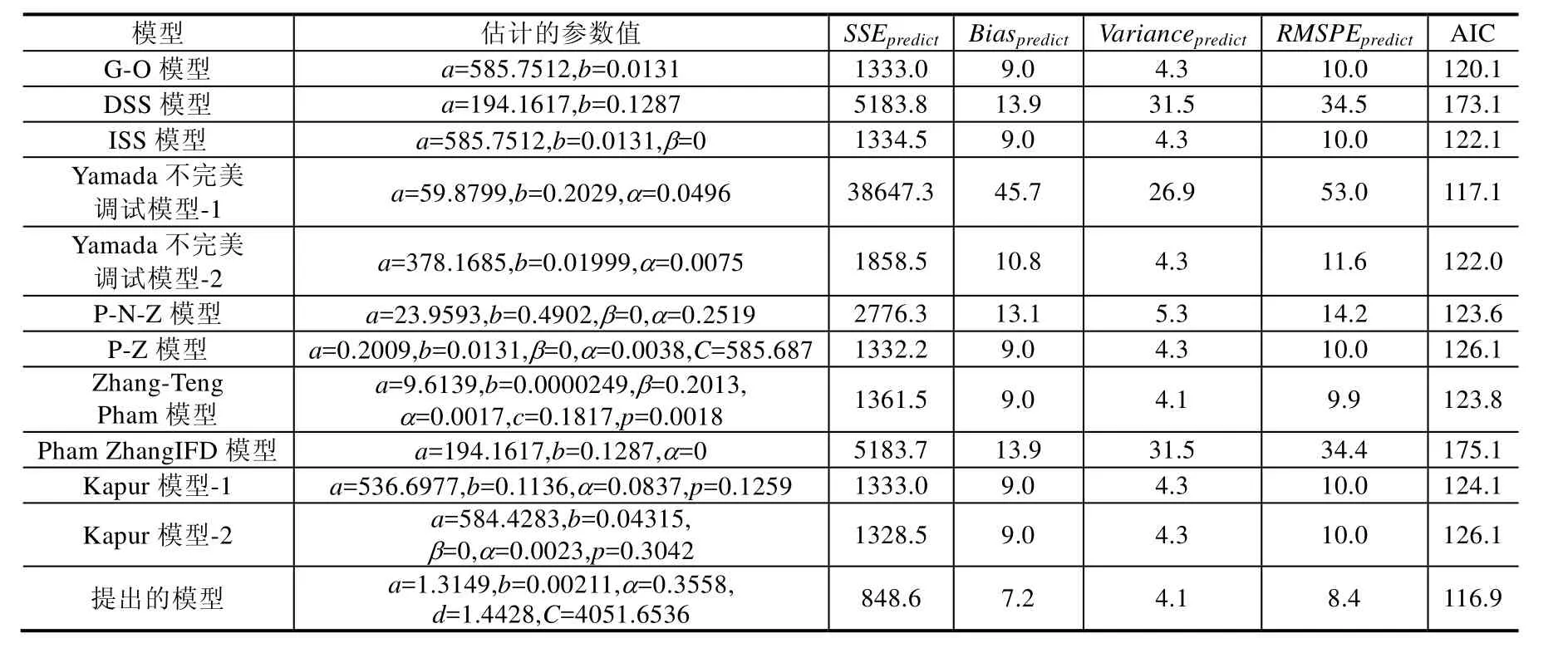
Table 4 Comparison results of different SRGMs for the second data set (63% of DS2)表4 第2组数据集上不同软件可靠增长模型的比较结果(63%故障数据)

从表5可以看到,在用80%的故障数据集时,与其他模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是 220.8;其次是Kapur模型-2,为364.0;最差是DSS模型和Pham Zhang IFD模型,为2091.2;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为 4.3;同时,G-O模型、ISS模型、Yamada不完美调试模型-1、Yamada不完美调试模型-2、P-Z模型、Zhang Teng Pham模型、Kapur模型-1和Kapur模型-2都是4.3;其次为P-N-Z模型,为6.9;最差为DSS模型和Pham Zhang IFD模型,为12.2;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为7.3;其次为P-N-Z模型,是7.5;最差为DSS模型和Pham Zhang IFD模型,都为28.4;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为 8.5;P-N-Z模型也为 8.5;其次为Kapur模型-2,为10.8;最差是DSS模型和Pham Zhang IFD模型,都为30.9;

· 有关 AIC值方面,提出模型的 AIC值也是最小,仅为 145.3;其次为Yamada不完美调试模型-2,是 147;最差是Pham Zhang IFD模型,为208.1.虽然Yamada不完美调试模型-2拟合得很好,它的AIC值和提出模型的 AIC值很接近,但是 Yamada不完美调试模型-2的SSEpredict,Biaspredict,Variancpredicte和RMSPEpredict的值却大于提出模型相应的值.因此,提出的模型在与其他的软件可靠性模型相比,故障拟合能力和预测软件发生故障的能力都要好于其他软件可靠性模型.

3) 数据集3(DS3)

从表6可以看到,在用60%的故障数据集时,同其他软件可靠性模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是351.37;其次是P-N-Z模型,为419.85;最差是Kapur模型-1,为 65503;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为 3.0;其次为 P-N-Z 模型,为 9.0;最差为Kapur模型-2,为 129.67;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为4.66;其次为P-N-Z模型,为4.73;最差为Kapur模型-1,为98.36;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为5.54;其次为P-N-Z模型,都为5.72;最差是Kapur模型-2,都为129.89;

· 有关 AIC值方面,提出模型的 AIC值也是最小,仅为 148.11;其次为 G-O模型,是 149.41;最差是 Pham Zhang IFD模型,为160.5.

Table 5 Comparison results of different SRGMs for the second data set (80% of DS2)表5 第2组数据集上不同软件可靠增长模型的比较结果(80%故障数据)

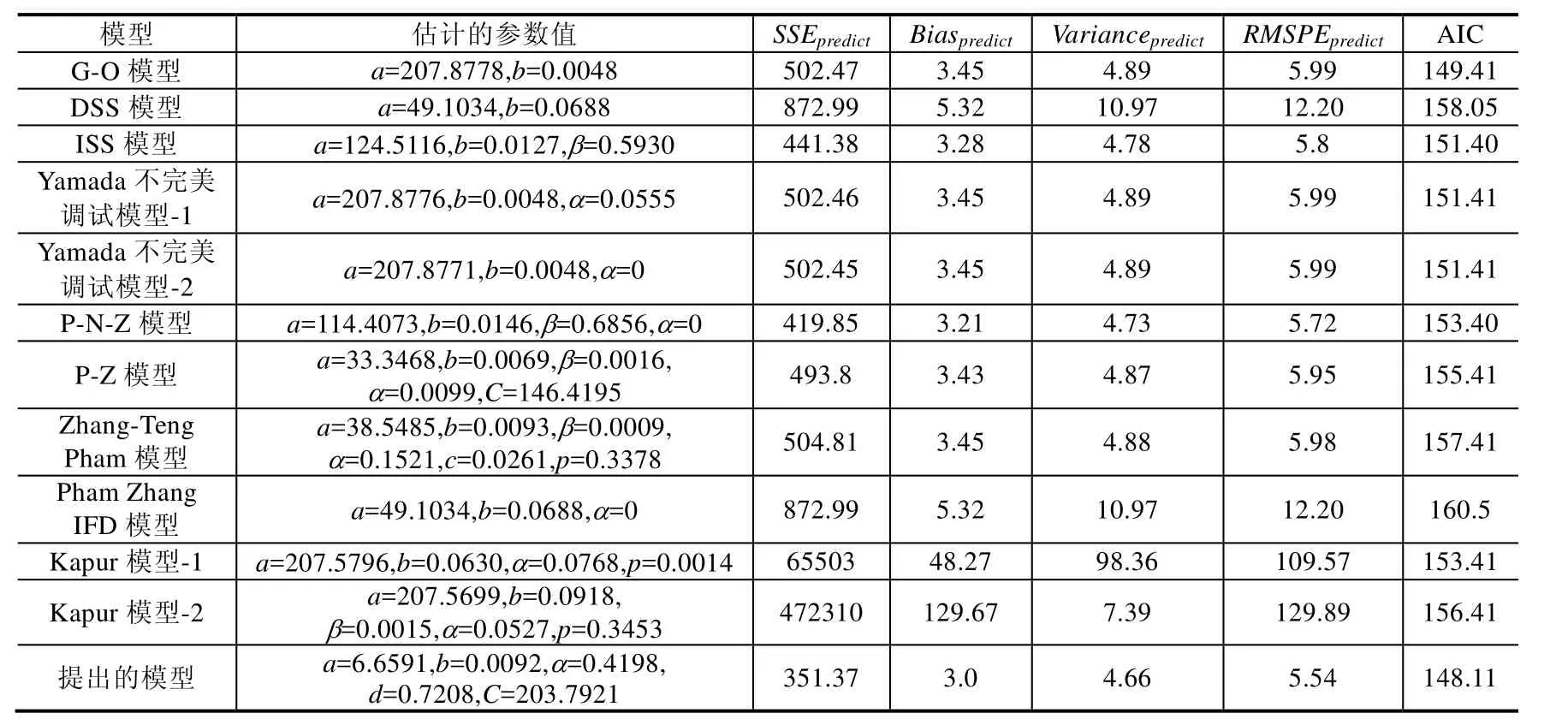
Table 6 Comparison results of different SRGMs for the third data set (60% of DS3)表6 第3组数据集上不同软件可靠增长模型的比较结果(60%故障数据)

从表7可以看到,在用80%的故障数据集时,同其他模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是6.7;其次是Pham Zhang IFD模型,为17.44;最差是Kapur模型-1为3943.9;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为0.61;其次为Pham Zhang IFD模型,为0.94;最差为Kapur模型-1,为16.57;

· 有关Variancepredict的值方面,提出模型和Pham Zhang IFD模型的Variancepredict的值都是0.84,为最小;其次为DSS模型,是1.14;最差为Kapur模型-1,为2.80;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为1.04;其次为Pham Zhang IFD模型,为1.26;最差是Kapur模型-1为16.8;

· 有关AIC值方面,提出模型的AIC值也是最小,仅为188.67;其次为G-O模型,是190.01;最差是DSS模型,为 198.61.

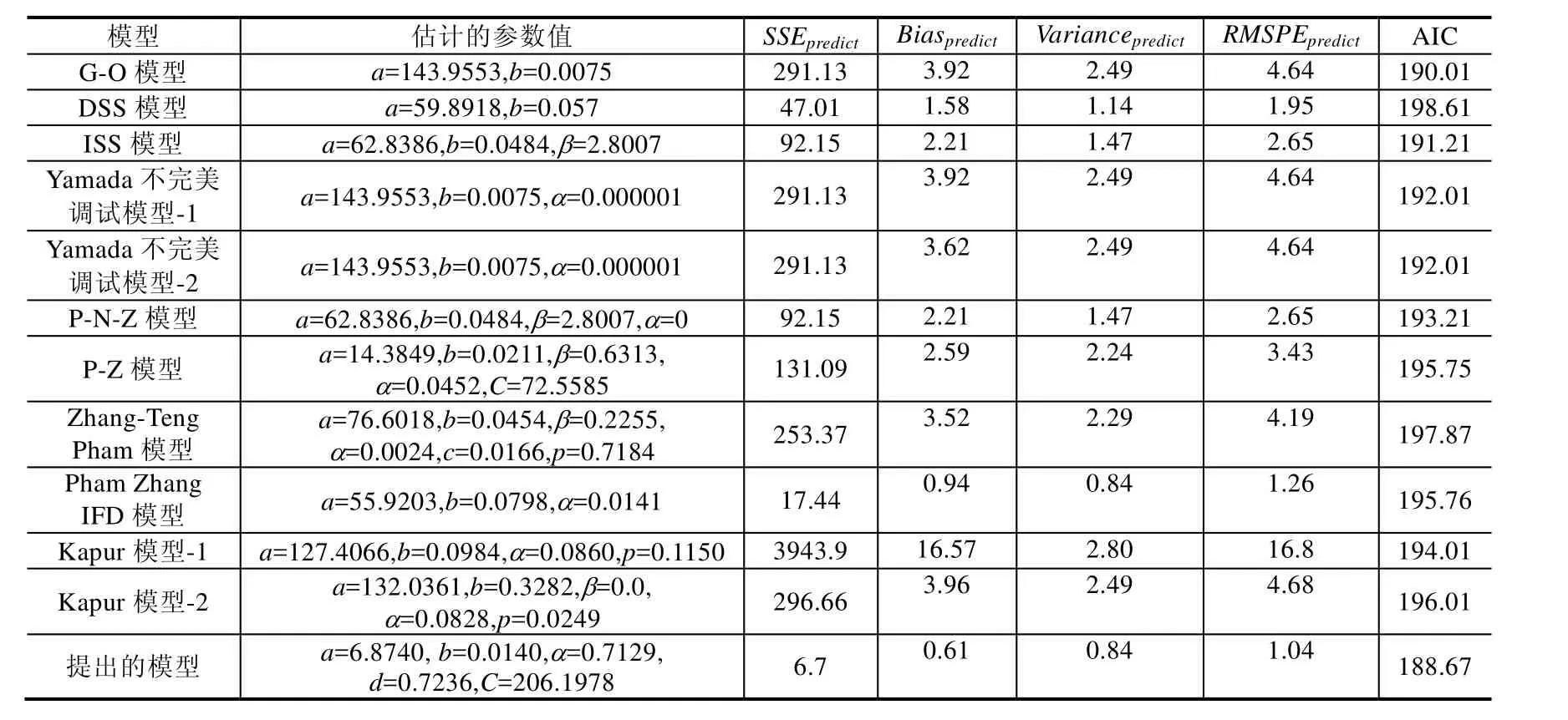
Table 7 Comparison results of different SRGMs for the third data set (80% of DS3)表7 第3组数据集上不同软件可靠增长模型的比较结果(80%故障数据)

图 4(a)和图 4(b)给出提出模型使用故障数据集 3的 60%和 80%进行故障拟合和预测的 95%的置信区间,我们能看到:估计的故障数量很好地落在 95%的置信区间内,而且提出的模型很好地拟合故障数据,并很好地预测软件发生故障的行为.

4) 数据集4(DS4)

从表8可以看到,在用60%的故障数据集时,同其他软件可靠性模型相比,我们能看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是 322.1;其次是 Yamada不完美调试模型-2,为1181.5;最差是Kapur模型-1,为2878.6;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为2.74;其次为 Yamada不完美调试模型-2,为4.63;最差为Kapur模型-1,为29.57;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为1.67;其次是Yamada不完美调试模型-2,为 10.02;最差为 Kapur模型-1,为 60.29;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为3.21;其次为Yamada不完美调试模型-2,是11.04;最差是Kapur模型-1为67.15;

· 有关AIC值方面,提出模型的AIC值也是最小,仅为 101.76;其次为G-O模型,是 102.58;最差是Pham Zhang IFD模型,为131.24.提出的模型在与其他软件可靠性模型相比,有更好的故障拟合和预测性能.

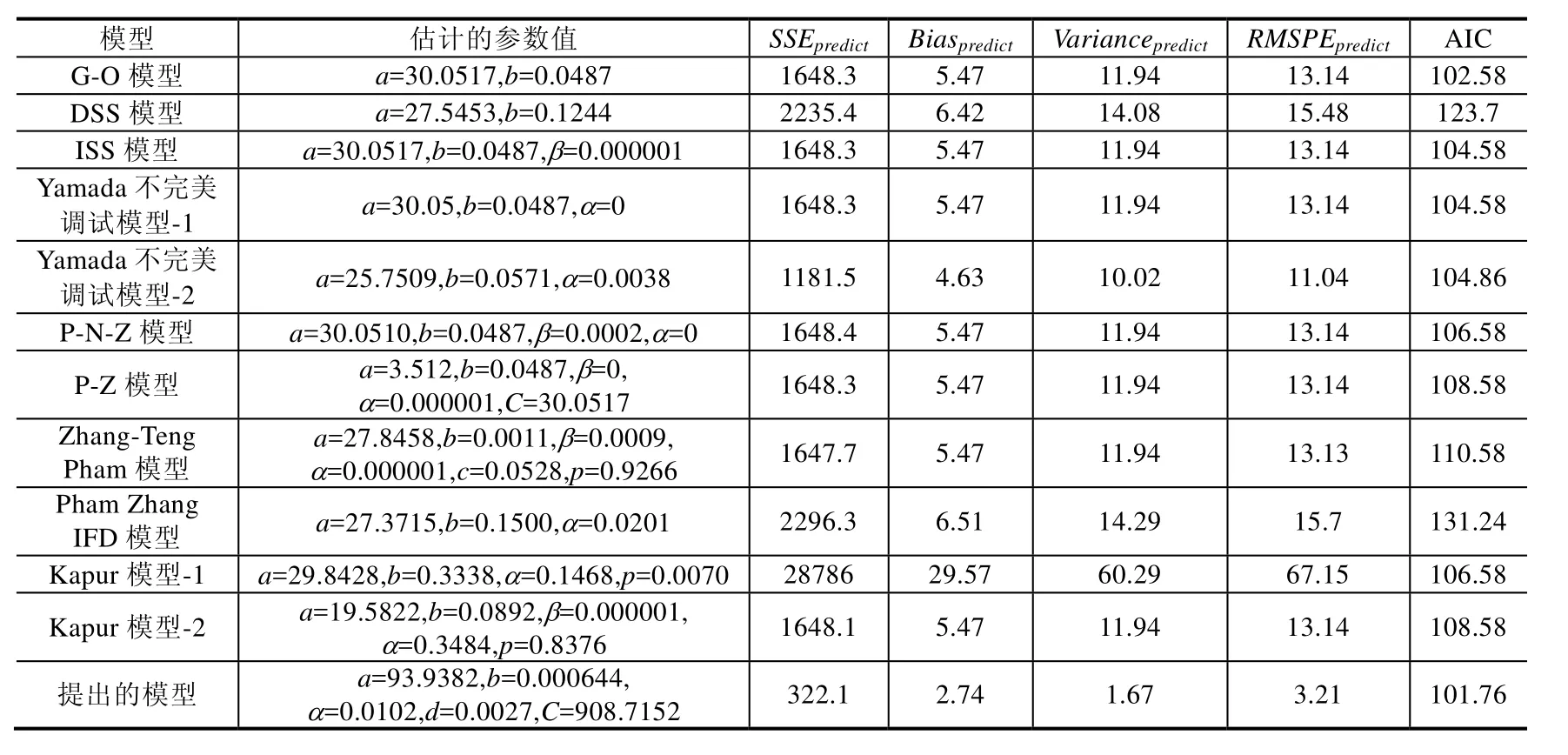
Table 8 Comparison results of different SRGMs for the fourth data set (60% of DS4)表8 第4组数据集上不同软件可靠增长模型的比较结果(60%故障数据)

从表9可以看到,在用80%的故障数据集时,与其他模型相比,我们能够看到:

· 有关SSEpredict的值方面,提出模型的SSEpredict的值最小,是 59.42;其次是 Yamada不完美调试模型-1,为335.56;最差是Yamada不完美调试模型-2,为16269;

· 有关Biaspredict的值方面,提出模型的Biaspredict的值最小,仅为1.71;其次为 Yamada不完美调试模型-1,为4.37;最差为Yamada不完美调试模型-2,为31.08;

· 有关Variancepredict的值方面,提出模型的Variancepredict的值最小,为3.45;其次为Yamada不完美调试模型-2,是7.37;最差为Pham Zhang IFD模型,为13.72;

· 有关RMSPEpredict的值方面,提出模型的RMSPEpredict的值最小,仅为3.85;其次为Yamada不完美调试模型-1,为10.11;最差是Yamada不完美调试模型-2,都为31.94;

· 有关 AIC 值方面,提出模型的 AIC值也是最小,仅为 124.98;其次为 Yamada不完美调试模型-2,是128.07;最差是Pham Zhang IFD模型,为166.81.提出的模型在同其他的软件可靠性模型相比,故障拟合能力和预测软件发生故障的能力都要好于其他软件可靠性模型.

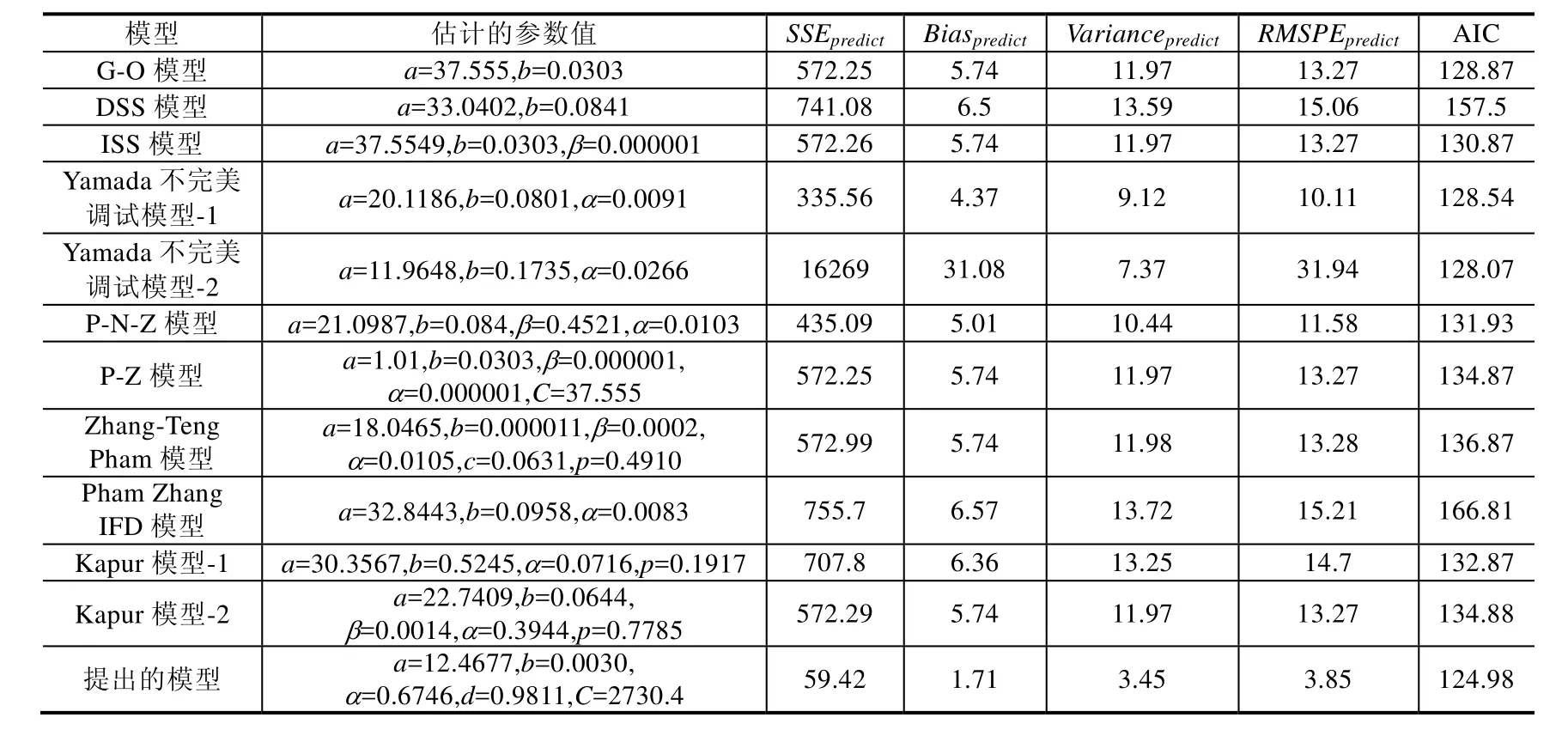
Table 9 Comparison results of different SRGMs for the fourth data set (80% of DS4)表9 第4组数据集上不同软件可靠增长模型的比较结果(80%故障数据)

从图4(c)和图 4(d)可以看出:提出的模型不论是用60%的故障数据,还是用80%的故障数据时,估计的故障数据都很好地位于 95%的置信区间内;另外,提出的模型也很好地拟合故障数据,并且准确地预测软件发生故障的行为.因此,无论是在软件故障拟合还是在软件故障预测方面,提出的模型都有很好的性能.

3.5 提出模型优于其他模型机理的分析

从以上的实验结果可以看到,提出的模型性能明显优于其他模型,包括完美调试模型和不完美调试模型.

提出的模型优于其他模型的机理分析如下.

① 考虑故障引进的情况,是提出的模型性能优于完美调试模型性能重要原因之一.

例如,完美调试模型包括G-O模型、DSS模型和ISS模型.由于软件测试和调试的复杂性,例如有客观因素——测试环境的多样性和软件编写的复杂性,有主观因素——测试者或调试者的技术以及心理因素等,故障引入很大程度上是由于软件复杂性造成的(客观因素),以及调试者对软件复杂性没有深刻认识(主观因素),另外也与调试者的技术也有一定关系(主观因素).当软件发布日期临近时,调试者的心理也会产生巨大压力,调试者的心理也会发生巨大变化(主观因素),在这种压力下,当检测出的故障被去除时,很可能引进新的故障.考虑故障被完全去除,而没有引进故障的假设是完全不符合实际的故障被去除的情况.因此,用完美去除故障的假设来建立软件可靠性模型在与我们提出的不完美调试模型进行性能比较时,考虑故障引进的情况,是提出模型的性能优于完美调试模型性能重要原因之一.

② 考虑故障引进多种变化的情况,是提出模型性能优于其他不完美调试模型性能的重要原因.

例如,其他不完美调试模型包括Yamada不完美调试模型-1、Yamada不完美调试模型-2、P-N-Z模型、P-Z模型、Zhang-Teng Pham模型、Pham Zhang IFD模型、Kapur模型-1和Kapur模型-2,由于故障引进的复杂性,故障引进率可能表现为随着测试时间逐渐下降,或者故障引进率随测试时间表现为先增后减的变化,或者故障引进随测试时间无规律变化等.其他不完美软件调试模型只考虑故障引进率的一种变化,不是为常数就是随测试时间下降,完全没有考虑到故障引进的其他变化.而我们提出的模型可以考虑故障引进率为多种变化,既可以为随测试时间下降,还可以随测试时间有先增后减的变化.因此,提出的模型更能适应复杂的测试和调试的情况,有更强的鲁棒性和稳定性,不易受到故障数据集噪音的干扰.而其他的不完美调试模型则受限于故障引进率的单一变化,在某些情况下会表现的很不稳定,适应性和鲁棒性也会很差.因此,考虑故障引进多种变化的情况,是提出模型性能优于其他不完美调试模型性能的重要原因.

③ 考虑故障引率非线性变化,是提出模型性能优于其他不完美调试模型性能的另一个重要原因.

为建模方便,Zhang-Teng Pham模型、Pham Zhang IFD模型、Kapur模型-1和Kapur模型-2假设故障引进率为常量;Yamada不完美调试模型-2和P-N-Z模型也假设故障引进率为常量,并且故障内容函数(故障总个数)随测试时间线性变化.由于故障引进的复杂性,故障引进率极有可能表现为非线性变化,而不是线性变化或者常量.而我们提出的模型正是假设故障引进服从 Weibull分布,故障引进率随测试时间表现为非线性变化.虽然Yamada不完美调试模型-1和P-Z模型的故障引进率都随测试时间表现为非线性变化,但是由于Yamada不完美调试模型-1是假设故障引进率随测试时间逐渐增长,这种情况与实际调试情况不符.因为在软件测试过程中,引进的故障会越来越少,所以故障引进率不会随测试时间逐渐增长.另外,P-Z模型假设故障引进服从指数分布,但是由于我们提出模型假设故障引进服从Weibull分布包含指数分布的特殊情况,所以我们提出的模型能更好地适应软件测试和调试情况,提出模型的性能也会好于Yamada不完美调试模型-1和P-Z模型的性能.

综上所述,提出的模型优于其他模型的原因为:一是提出的模型考虑故障引进的情况,更符合实际的软件测试和调试过程;二是假设故障引进服从Weibull分布,能够包括更多在软件测试和调试过程中故障引进率变化情况;三是假设故障引进率非线性变化更符合故障引进随测试复杂变化的情况.

3.6 提出模型的参数敏感性分析

一般来说,模型的参数比较多时,需要进行模型的参数敏感性分析[25].主要目的是考察哪些参数对模型的评估效果和预测有重要影响,也就是考察一下模型的鲁棒性(robust).而具体使用的方法就是改变模型的某个参数值,模型其他参数则保持不变.图5(a)～图5(e)显示出提出模型的参数a,b,α,d和C的敏感性分析的情况.

从图5(a)、图5(b)和图5(e)中可以清晰地看到,提出模型期望估计的累计检测出的故障数量随着期望最终引进故障的数量a、故障检测率b和期望最初存在软件中的故障数量C的变化而大幅度地发生变化.因此,提出模型的参数a,b和C都是有影响的参数.

4 结束语

本文介绍Weibull分布的相关概念和表示方法,然后分析在软件调试过程中,故障引进服从Weibull分布的原因.在此基础上,用Weibull分布进行故障引进过程的相应模拟,并提出一个基于Weibull分布引进故障的软件可靠性增长模型,同时给出相应的模型推导过程.为了验证提出模型的拟合故障数据和预测软件中故障发生数量的能力,本文给出了相应的故障数据集和有关的模型性能比较标准,并对提出的模型用最大似然估计法进行相应的模型参数估计.实验结果表明:提出的模型在与多种软件可靠性增长模型(包括完美调试软件可靠性增长模型和不完美调试软件可靠性增长模型)比较后,有更好的故障拟合效果和更准确地预测软件故障发生数量的能力.为了考察提出模型的参数变化对软件可靠性评估和软件故障预测的影响程度,我们也给出相应的参数敏感性分析.参数敏感性分析实验的结果表明,提出模型的参数a,b和C都是有影响的参数.

考虑到实际测试过程中检测到的故障不是被立即和完美地去除,而是在检测和去除故障之间会存在时间延迟,在去除故障时可能引进新的故障,因此,未来的研究将在本文研究的基础上,就故障排错延迟问题进行深入研究.

致谢在此,我们感谢审稿专家对本文提出的宝贵建议.