简化模型下基于Terminal滑模的纵向着舰控制律设计*

（91404部队 秦皇岛 066000）

1 引言

舰载机着舰具有非常高的风险性，舰载机驾驶员完成艰巨的作战任务后心神疲惫，并且在着舰过程中还会受到型误差、舰岛尾流扰动、航母横纵摇等因素的影响，导致人工着舰难度很大，由此自动着舰技术应运而生，其中舰载机着舰控制系统（Automatic Carrier Landing System，ACLS）［1］在自动着舰过程中发挥着至关重要的作用。舰载机着舰控制系统要实现精确着舰的目标，最重要的一点是要具有较快的响应速度及较强的鲁棒性。

传统的PID控制结构简单、易于工程实现，但是其参数设计在一定程度上依赖于试凑和经验［2］，其参数无法随舰载机姿态改变而调整，所以系统的鲁棒性较差。滑模控制［3］是一种变结构的控制方法，它可以使系统在滑模面上作小幅滑动模态运动，处于滑模运动的系统具有很好的鲁棒性。由于滑模控制具有较好的快速性与一定的鲁棒性，很多学者对其在飞行器姿态控制器中的应用进行了研究［4～5］。

考虑到滑模面中引入积分项，有利于减少静差，而Terminal滑模的有限时间到达特性［6～7］，又能进一步提高系统的响应速度。因此本文以F/A-18A舰载机为研究对象，提出一类由误差、误差积分、误差Terminal项综合而成的积分型Terminal滑模控制方法，以进一步提高飞行俯仰通道姿态控制的品质，然后根据Lyapunov稳定性理论分析其稳定性，最后采用Matlab/Simulink仿真验证该Terminal滑模控制方法的正确性和有效性。

2 模型描述

在设计舰载机着舰控制系统时，必须考虑舰上着舰等特点，与飞机陆上着陆有一个平飘过程不同，舰载机采用等角下滑的方式进行着舰［8］，也就是说着舰控制系统如果能使舰载机下滑的姿态角保持恒定［9］，就可以帮助舰载机精确着舰，保证着舰安全。

考虑到舰载机着舰过程中，舰载机处于等下滑角的直线运动状态，并且飞行速度较慢，因此可以认为舰载机在此时的气动特性是线性的。首先对舰载机着舰过程进行受力分析，舰载机在着舰过程中主要受到自身的重力、发动机推力、空气阻力及升力，如图1。

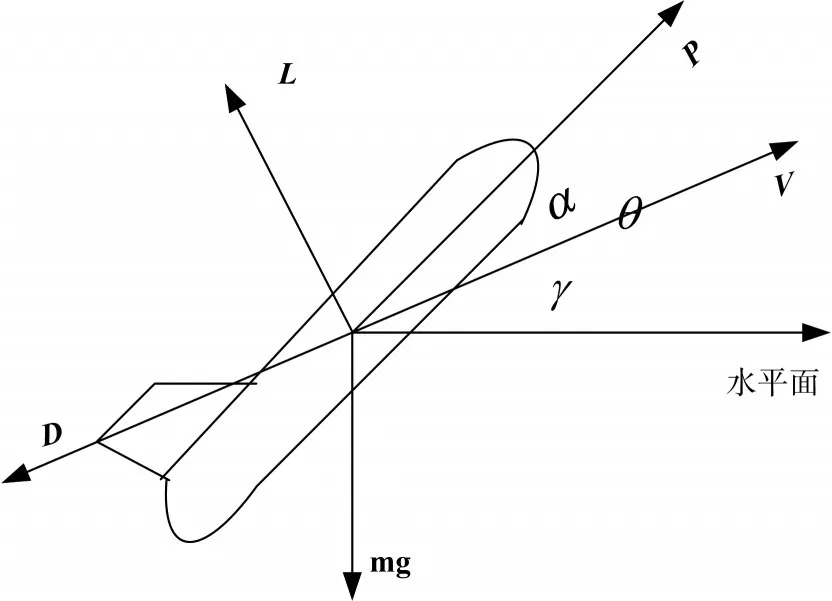
图1 舰载机受力分析图

根据舰载机受力情况，可得到如下动力学方程：

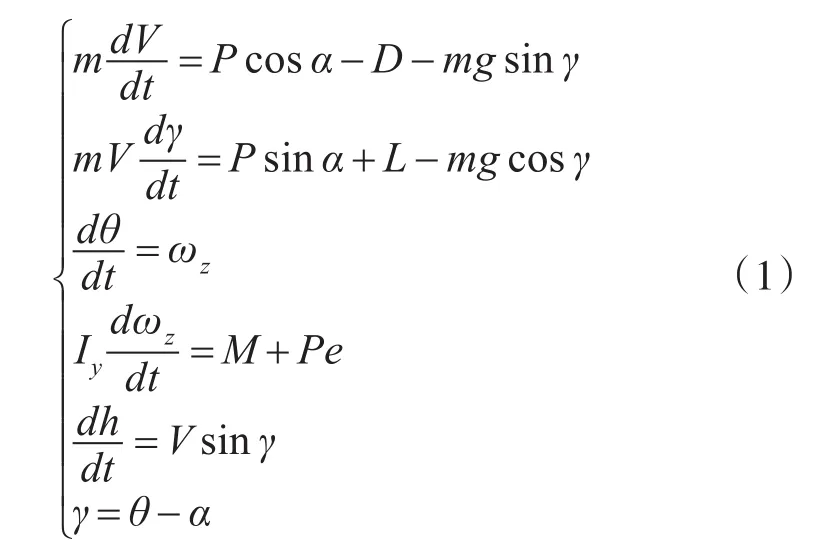
其中，m是舰载机质量，γ是速度倾角（航迹高低角），P是发动机推力，D是气动阻力，L是气动升力，g是重力加速度，Iy是俯仰转动惯量，M是气动俯仰力矩，e是推力偏心距，v为舰载机的飞行速度，α为舰载机的迎角，θ为舰载机的俯仰角，ωz为舰载机的俯仰角速度，h为舰载机的高度，δp为舰载机的油门杆偏转角，δz为舰载机的升降舵偏转角。

由动力学方程可推出舰载机着舰过程中的纵向控制状态方程，可描述为

其中x=[v，α，ωz，θ，h]T，u=[δp，δz]T。

3 Terminal滑模控制律设计

Terminal滑模由于在机理上具有有限时间到达原点附近邻域的特性，比传统的PID控制，具有优越的收敛特性，引起了广大学者的注意［10～11］。

假设舰载机着舰过程中各个控制变量的期望为xd=[vd，αd，ωzd，θd，hd]T。

为减少静差与加快响应速度，设计一类积分型Terminal滑模面为

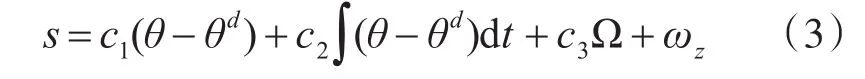
其中ωz=，Ω 为Terminal项，为避免控制奇异，选取

假设在控制律的作用下，滑模面到达0，则有：

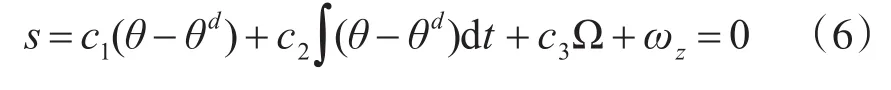
考虑到舰载机着舰过程中舰载机姿态角基本保持恒定，设计反馈误差：e=θ-θd，则有=。

则可以得到整理为

进一步整理得：

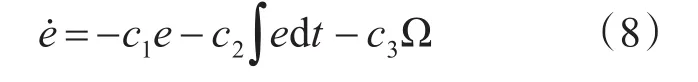
选取Lyapunov函数为

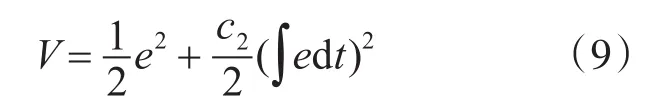
求导得：

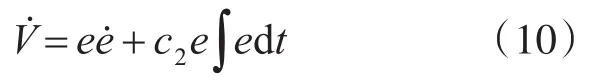
又由上述滑模面定义得：

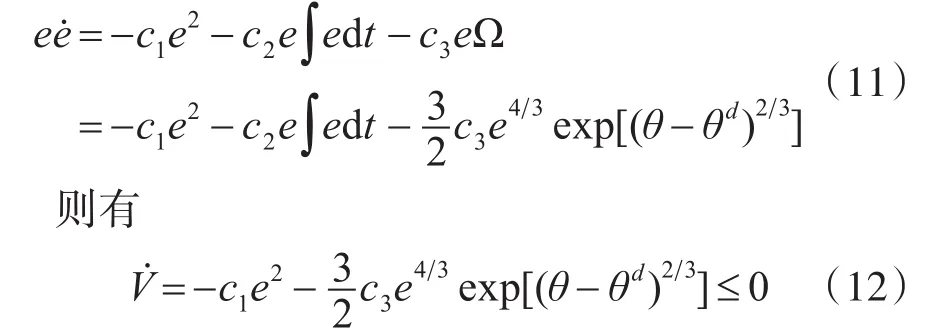
显然当滑模面到达0后，取c1≥0，c3≥0可以保证e→0，则表明上述积分型Terminal滑模面设计是合理的。

对上述积分型Terminal滑模面求导得：

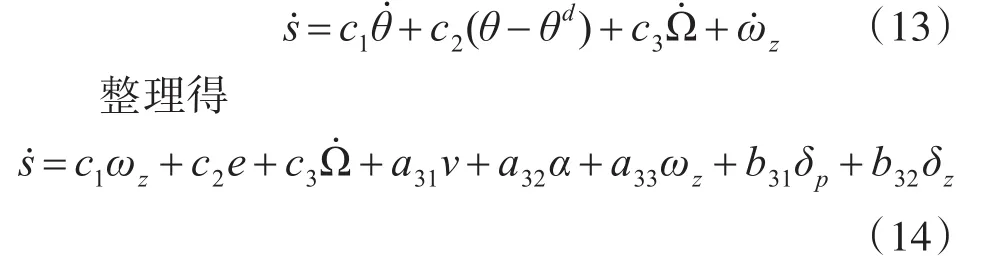
采用控制量的解耦设计，即δz控制垂向运动，δp控制前向运动，则设计：

此时选取控制系数a0足够大，可以保证系统的局部有界。考虑给定状态x在局部区域内有|x|＜d，此时有a31+a32有界，则存在足够大的a0使得Lyapunov函数导数小于0，从而系统稳定。

4 仿真实验

为了验证本文提出的舰载机着舰控制律的有效性和实用性，本文以F/A-18A舰载机为研究对象［12］，界扰动，分别采用本文提出的控制方法与传统的PID控制方法进行仿真，两者的仿真结果如下。

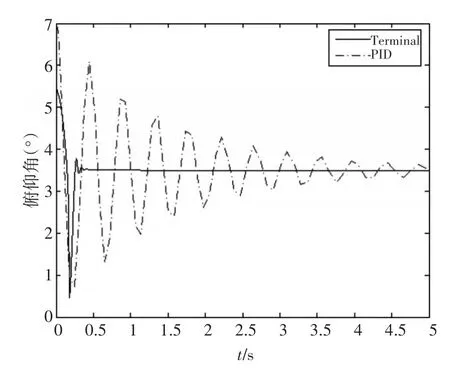
图2 舰载机俯仰角

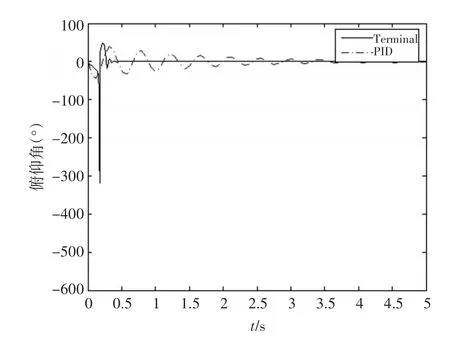
图3 舰载机俯仰角速度

图4 舰载机飞行高度

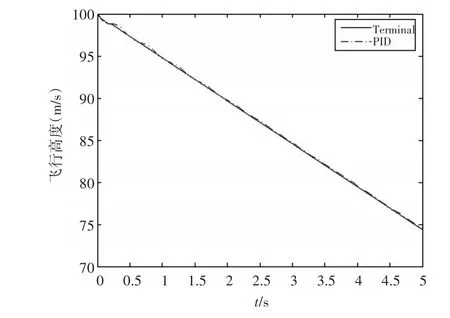
图5 舰载机飞行速度

以上仿真曲线中实线表示采用积分Terminal滑模控制方案仿真结果，虚线表示传统PID控制方法仿真结果，从俯仰角响应曲线可知，采用积分Terminal滑模方法具有静差小响应快的优点。

5 结语

本文在舰载机着舰姿态模型的基础上，提出了一类新颖的积分Terminal滑模，从理论上证明了该滑模面的合理性。同时由于积分的引入，系统静差大大减少，而Terminal滑模的引入，大大加快了系统的响应速度。在控制器增益相同，所有初始条件完全一致的情况下，通过仿真比较分析，可以明显看出积分Terminal滑模确实具有更好的快速性与更小的静差。通过仿真结果表明该方法比较适合舰载机着舰过程的姿态跟踪控制。