基于模拟退火优化的直接航迹控制算法设计*

夏云鹏 杨田田

（1.中船重工第七一三研究所 郑州 450000）（2.武汉理工大学 武汉 430070）

1 前言

无人船［1］（Unmanned Surface Vessel，USV），是一种无人操作的水面船。它具有机动性强、速度快、自主化、无人化等特点，其主要功能是代替人执行一些特殊的、对人有危险的任务。

精准的航迹控制是无人船执行各项任务的基础保障，也是无人船运动控制领域的研究热点。无人船在实际航行环境中会受到外部干扰的影响，导致产生模型不确定性的问题。

无人船航迹控制算法主要分为两类，一类是直接控制算法［2～3］，控制精度高，控制算法直接作用于航迹，算法复杂度高；一类是间接控制算法［4～6］，其设计思路是将航迹控制问题转化为航向控制问题，主要实现方式是将其分解为双闭环控制系统，内环由传统的航向控制算法构成，外环则使用航向解算算法，控制精度相对较低，但优点是可直接使用已有的自动舵技术，更有利于工程应用［7］。

针对无人船航迹控制中容易出现的非线性、时滞性问题，本文采用非线性模型预测控制（NMPC）算法对水面无人船进行直接航迹控制，并采用模拟退火算法对预测控制算法进行最优控制序列求解，进一步提高航迹控制的准确性和实时性。模型预测控制采用反馈校正，可应对多种不确定性问题（包括系统干扰、模型失配等），并通过滚动优化策略在线求解局部最优化问题，极大地减少了在线优化计算量，提高算法的响应速度。

2 基于模拟退火优化NMPC算法的直接航迹控制

2.1 控制器设计

针对无人船航迹控制中容易出现的非线性、时滞性问题，本节采用非线性模型预测控制（NMPC）算法对水面无人船进行直接航迹控制，并采用模拟退火算法对预测控制算法进行最优控制序列求解，进一步提高航迹控制的准确性和实时性。非线性模型预测控制器总体流程如图1。

图1 非线性模型预测控制器总体流程

基于NMPC的航迹控制器根据预设航迹信息以及无人船的初始状态信息，直接控制无人船的航迹。在基于NMPC的水面无人船航迹控制系统中，航迹控制器的输出量为无人船的舵角控制量以及航速控制量，收到无人船的状态量反馈信号（包括无人船的位置坐标信息，以及航向角信息），对航迹控制器内部预测输出值进行自我校正，并采用模拟退火算法进行局部寻优获得下一时刻的无人船舵角控制量以及航速控制量信息［8］。NMPC航迹控制器主要包括无人船预测模型、目标函数以及约束信息三个方面。下面将从这三个方面来介绍控制器的设计内容。

基于非线性模型预测控制的无人船航迹控制系统的控制流程如图2所示。首先对预设航迹信息进行离散化处理，获得离散化后的第一个目标航迹点信息，基于NMPC的航迹控制器根据此目标航迹点信息进行动作，计算无人船舵角控制量以及所需航行速度，进行航迹跟踪，获取离散化后的航迹信息上的下一个航迹点，重复以上动作，直到经过离散化后的航迹信息上的最后一个点。

2.2 无人船预测模型

一般来说，无人船的运动情况需要使用六个自由度来描述，包括横摇、纵摇、艏摇、横荡、纵荡、垂荡。为描述无人船在六自由度中的运动情况，需建立如图3所示的无人船坐标系，包括固定坐标系o-x1y1z1（简称“定系”）和运动坐标系G-xyz（简称“动系”）。“定系”是指固定于地球上的惯性坐标系。“动系”是指跟随船体运动的附体坐标系，原点设在无人船的船体重心G处，Gx为无人船水平面方向，Gy为无人船横剖面方向，Gz为无人船的纵中剖面方向。正方向按右手系的规定。

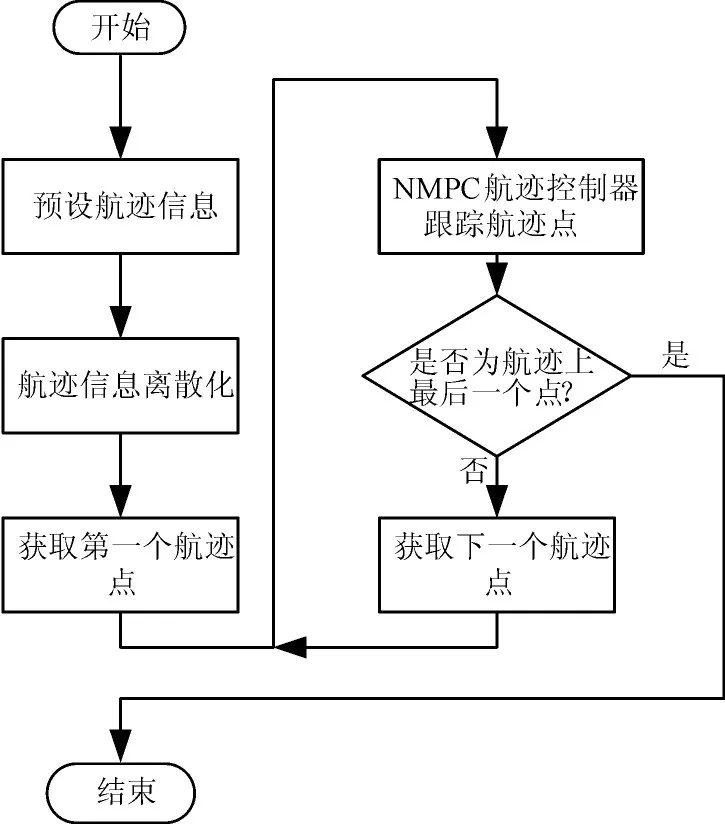
图2 直接航迹控制算法流程图

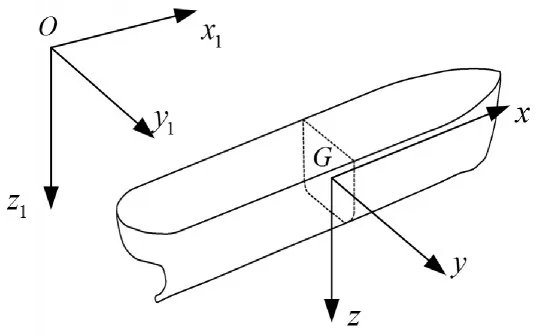
图3 无人船坐标系

表1 无人船运动参数

无人船在附体坐标系G-xyz和惯性坐标系o-x1y1z1中涉及到的运动参数如表1所示。其中X，Y，Z为无人船所受外力在附体坐标系G-xyz上的投影；K，M，N为无人船力矩在附体坐标系G-xyz上的投影；u，v，w为无人船的速度在附体坐标系G-xyz上的投影；p，q，r为无人船的角速度在附体坐标系G-xyz上的投影；(x，y，z) 为无人船重心在惯性坐标系o-x1y1z1的空间坐标；φ，θ，ψ为无人船在惯性坐标系o-x1y1z1中的三个欧拉角，φ称为横倾角、θ称为纵倾角、ψ称为方位角。

船舶在海洋上的航行情况既可以采用“动系”中的速度向量u，v，w和角速度向量p，q，r来表示，也可以使用定系中位置向量的导数，，及欧拉角姿态向量的导数来表示。研究者可根据自身课题研究需要确定表示方式。另外，船舶中的“动系”和“定系”之间还存在如下变换关系［5］。

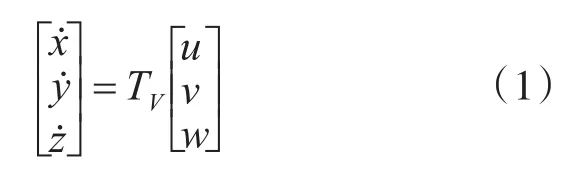
其中，变换矩阵TV为

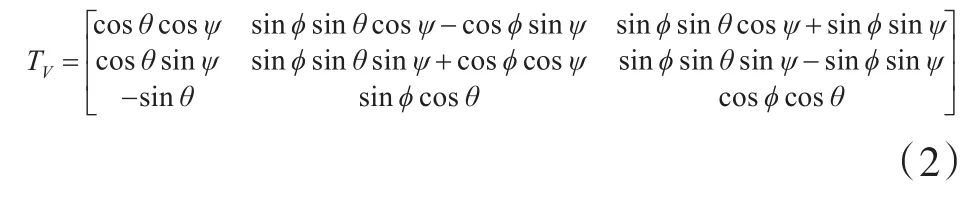
无人船的直接航迹控制器设计，重点关注无人船在水平面的运动，暂且忽略橫倾、纵倾和升沉对无人船运动的影响。因此将无人船的六自由度模型的式（1）和式（2）进行化简，得到无人船的三自由度模型为

其中，为无人船位置信息的横坐标的导数，为无人船位置信息的纵坐标的导数，为无人船艏向角的导数，ψ为无人船的艏向角，u为无人船速度的纵向分量，v为无人船速度的横向分量，r为无人船的角速度。

水面无人船航行过程中，当满足u≫0且v≈0时，可忽略横漂角对无人船运动的影响，此时方程可进一步简化为

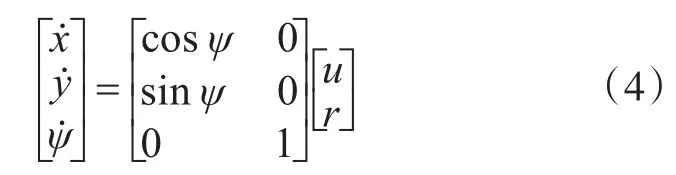
又已知无人船角速度r和舵角δ之间的关系可用式（5）表示。式（5）中，K表示无人船的旋回性指数，T表示无人船的追随性指数。K、T的值可由无人船的Z形操纵性试验获得，具体计算方法见文献［9］。

将式（5）带入式（4）中，并以为采样时间Ts进行离散化处理，可得差分方程为

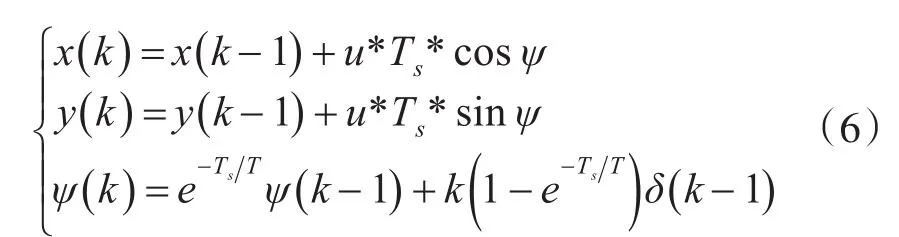
在水面无人船的航迹控制中，若令状态量的矩阵形式为χ=[xyψ]T、控制量的矩阵形式为u=[uδ]T，根据式（6）表示的无人船输入控制量与输出状态量之间的关系，可以得出无人船的非线性离散模型的一般表示为

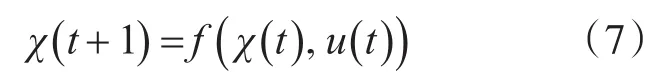
2.3 目标函数

基于非线性模型预测控制的航迹控制器中，目标函数的选取要能够充分反映无人船航迹跟踪参考航迹的程度。本文参考文献［10］中阐述的软约束方法，结合无人船航迹控制的预测模型，设计目标函数如下：

其中，Hp是MPC航迹控制器的预测时域，Hc是MPC航迹控制器的控制时域，ρ为权重系数，ε为松弛因子。

该目标函数既考虑了无人船对预设航迹的跟踪能力，也考虑了控制量增量的约束，有效地避免了控制量的突变。另外，在目标函数中加入了松弛因子，可以防止出现没有可行解的情况。

2.4 约束条件

根据无人船本身的控制特点，在输出控制量的过程中要考虑舵角约束以及航速约束。本文中使用的无人船模型舵角以及舵角控制量增量约束为

本文中使用的无人船航速以及航速增量约束为

综上所述，无人船非线性航迹控制问题可以用以下有限时域内的最优化问题来表示：

2.5 算法流程与步骤

优化算法的实时性以及准确性直接影响所设计的航迹控制器的控制效果，由于非线性目标函数较难求得解析解，此处针对式（11）所示的局部最优化问题，采用模拟退火算法进行最优控制序列求解，具体求解步骤如下：

1）初始化参数：初始温度T0，降温速率q，结束温度Tend，对应于每个温度T的迭代次数L，以当前时刻的控制量矩阵作为初始可行解矩阵u0；

2）对当前温度T，求解局部最优解，即重复步骤3）至6）；

3）对当前可行解矩阵u0在控制量约束范围内随机产生一个新解u1；

4）对应于式（11）所示的目标函数J，求解其对应于可行解矩阵u0和u1的增量dJ=dJ(u1)-dJ(u0)；

5）根据判断条件确定当前局部最优解，即若dJ＜0，则认为新解u1为最优解，用u1替代u0；否则，计算对于新解的接受概率exp(-df T)，当满足接受概率exp(-df T)＞rand（rand为（0，1）区间上的随机数）时，也认为新解u1为最优解，用u1替代u0；否则，仍认为u0为最优解。

设置终止条件，使得温度T衰减至结束温度Tend时，输出当前的最优解u0，不满足终止条件时，对当前温度T按降温速率进行衰减运算后，重复执行步骤2）。

3 仿真试验

3.1 试验船概况

本文中的实验船的基本参数如表2所示。

表2 无人船主要参数

在式（6）中无人船的旋回性指数K和无人船的追随性指数T可以通过对实验船进行10°10°的Z形操纵性试验来获得。在平静的湖面进行了实验船的Z形（10°10°）试验，获得的实验船艏向角和舵角关系变化曲线如图3所示，根据文献［11］中提到的计算方法，对无人船试验数据进行拟合，求得实验船的K、T参数的值为K=0.49，T=1.94。

3.2 仿真验证

针对表2提出的试验船参数，对设计的基于模拟退火算法改进的NMPC的航迹控制器进行航迹控制效果仿真。各项参数设置为

1）无人船初始状态：位置坐标(0 ，-22)，航向角ψ=0°，航速v=0m/s。

2）预设曲线航迹信息：原点为(0 ，0)、半径为20m的圆弧轨迹。期望跟踪速度vd=3m/s。

3）设置采样时间为50ms。

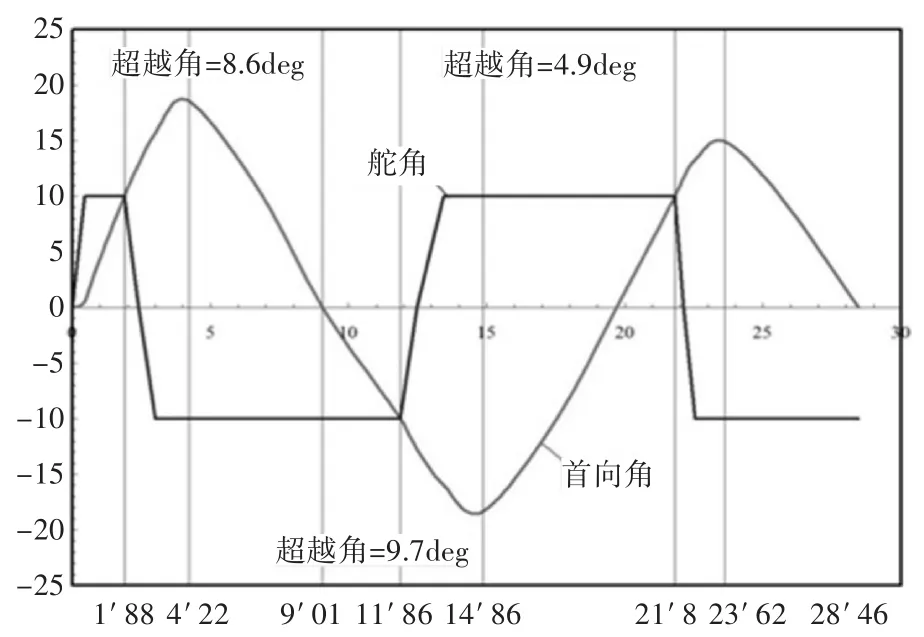
图4 Z形操纵试验结果

仿真试验分别在无干扰和有干扰情况下进行仿真验证。对于有干扰情况，外部干扰信号设置为无人船航速的25%，干扰信号对无人船的航迹控制系统产生的影响可用式（12）表示：

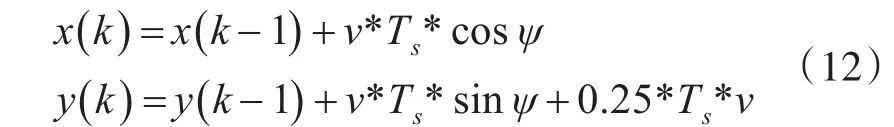
其中，Ts为采样时间。此处取Ts=1。

无干扰条件下，对于预设圆弧形航迹，航迹跟踪仿真实验获得的结果如图5至图7所示。

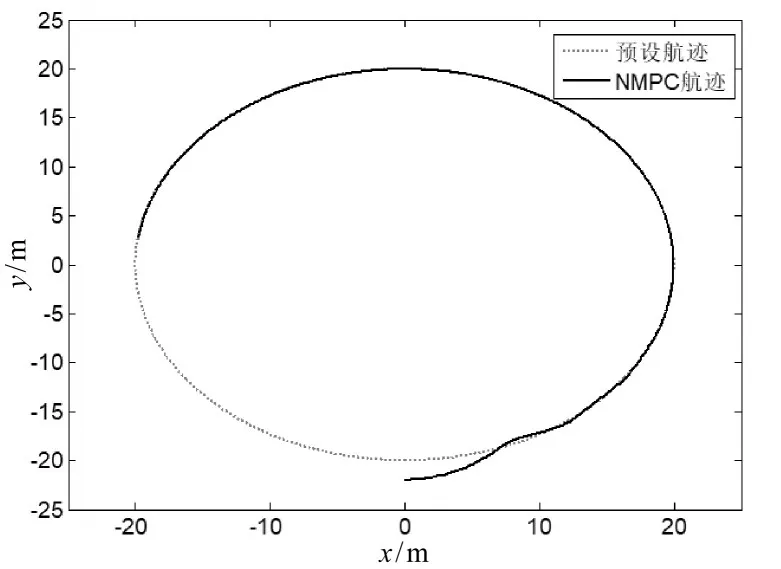
图5 航迹跟踪效果

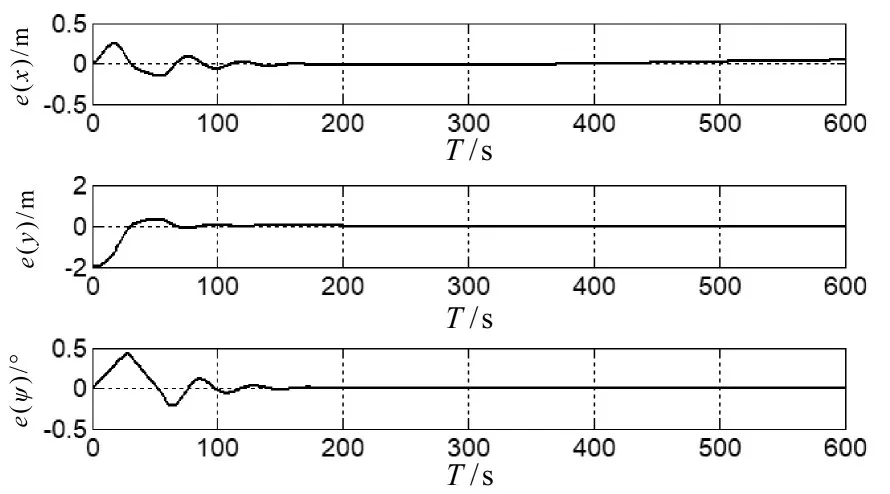
图6 状态量误差变化曲线

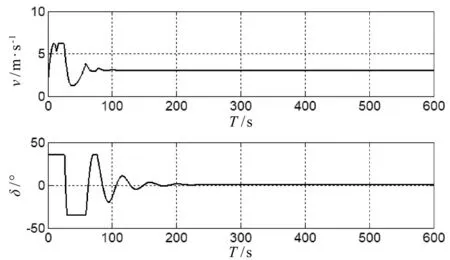
图7 控制量变化曲线

由航迹跟踪效果图和状态量误差变化曲线可以看出，对于设定的圆形航迹，基于NMPC的直接航迹控制器可以根据当前时刻无人船的状态信息，调整无人船的舵角控制量和航速控制量，快速地跟踪到设定航迹，且最终的跟踪误差为零。由控制量变化曲线可以看出，在无人船由接收到设定圆形航迹信息时刻的位置进行航迹跟踪时，舵角控制量以及航速控制量会立刻做出响应，直到无人船跟踪到预设航迹上，航速稳定在期望航速上，舵角控制量以及航速控制量保持不变，实现预设圆形航迹的精确跟踪控制。

对所设计的航迹控制器添加干扰信号，参考式（4）～（5）所示，设置对应于无人船实时航速的干扰信号，获得的航迹控制曲线以及过程中的干扰信号曲线如图8～图11所示。

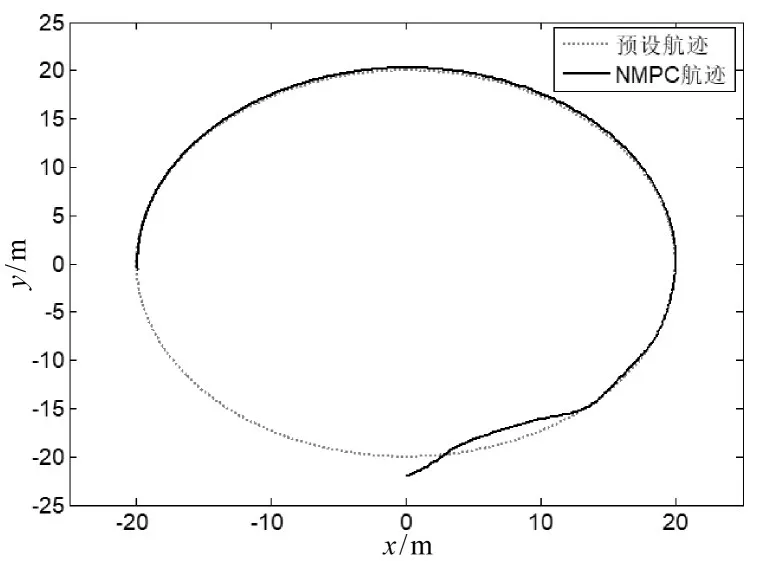
图8 曲线航迹跟踪效果（有干扰）

在有干扰的情况下，由航迹跟踪效果图可以看出，在无人船接收到预设航迹信息初期，航迹跟踪效果较差，但是基于NMPC先预测后控制的思想，一段时间后基于NMPC-SA的航迹控制器对干扰信号进行了预测补偿，控制效果慢慢变好，到后期基本上能通过舵角补偿量实现对预设圆形航迹的精确跟踪控制。

图9 状态量误差变化曲线（有干扰）

图10 控制量变化曲线（有干扰）

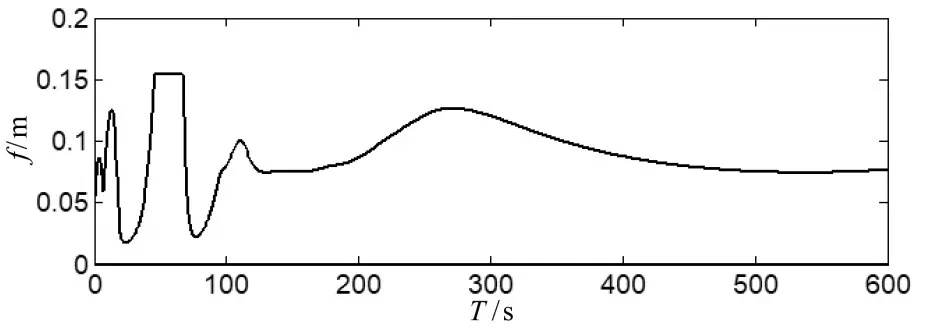
图11 扰动信号曲线图

4 结语

针对传统的粒子群算法容易陷入局部最优解的问题，利用模拟退火算法的突跳特性提出了一种改进算法，通过加入多目标优化，提升了算法的实用性。仿真结果显示，改进算法可以优化无人船自主航行的路径平滑度，提高路径的安全性，满足无人船全局路径规划的要求。针对无人船航迹控制中容易出现的非线性、时滞性问题，提出了基于非线性模型预测控制（NMPC）算法对水面无人船进行直接航迹控制，并采用模拟退火算法对预测控制算法进行最优控制序列求解，提升了算法的实用性。仿真结果显示，改进算法有效地提高了航迹控制的准确性和实时性。