我国股票市场复杂网络模型的“去噪”研究——基于随机矩阵理论

李 燕，洪振木

（安徽财经大学 金融学院，安徽 蚌埠 233030）

股票市场复杂网络模型是指以各股票为节点，以股票间的某种关系为连边而构成的复杂网络模型。经济的快速发展，信息的迅速传播使得股市对市场中利好、利空消息的捕捉更加敏捷。崔永元曝出有关明星艺人的阴阳合同以及偷税漏税事件使得华谊兄弟、唐德影视等娱乐公司股价连续下跌；长生生物问题疫苗的曝光使其股价迎来33 个跌停后退市，这都体现出股价对经济变化的敏感性。另外，由于上市公司的运营状况会直接引起股价的波动，而经济的增长或衰退具有滞后性，进一步显现出股市作为经济“晴雨表”的重要性。为此，许多经济学家用各种理论对股票市场进行了研究，复杂网络理论也成为学者分析股票市场的惯用工具。构建一个含有高质量信息的股票市场复杂网络模型是研究股票市场网络拓扑性质的基础，本文基于RMT 理论剔除构建网络矩阵的噪声信息来优化网络，通过对比网络优化前后的稳定性及投资组合风险差异来分析网络“去噪”效果。

一、文献综述

股票市场错综复杂，各主体间的相互作用随时间的变化而变化，时间序列的无限性，样本数据的有限性，导致噪声信息对样本数据间相关关系的干扰。股票市场各主体间相关系数矩阵所含有的噪声信息，不利于复杂网络理论准确地揭露其网络拓扑性质。RMT 理论的起源可以追溯至1928年J.Wisllart 在固定大小的Gatlaaian矩阵上所做的研究。[1]（P32-52）RMT 理论在金融领域的应用起源于1999年Laloux、Cizeau 等人发现的数据相关系数中噪声信息的存在，这些噪声会掩盖金融时间序列的经济意义。[2]（P1467）Laloux、Cizeau 等人提出将包含噪声信息的特征值用全部特征值的平均来代替的方法（LCPB法）以剔除噪声信息。Plerou、Gopikrishnana 和Rosenowb 等人在LCPB 法的基础上提出用数字0 代替包含噪声信息的特征值的方法（PG+法）来避免噪声信息的干扰。[3]（P66126）Sharifi、Crane 和Shamaie 等人在考虑了金融序列方向性的基础上，提出以最大正定特征值替换噪声特征值的方法（KR 法）来消除噪声因素的副作用，并以S&P500 指数的30 分钟高频数据确定相关矩阵中的噪声百分比，最后为投资组合优化提出了宝贵的意见。[4]（P629-643）韩华、吴翎燕等人在讨论金融相关系数矩阵和随机矩阵特征值统计特性的基础上，对现有的去噪方法进行改进，重构更适合构建复杂网络模型的相关系数矩阵，并建立金融网络模型。[5]（P439-448）骆旗、韩华、龚江涛等人针对小组合股票市场，提出使用蒙特卡罗模拟修正的随机矩阵“去噪”方法。[6]（P2642-2646）谢赤、胡珏、王钢等人运用RMT 理论和相关系数动态演化模型建立全球股指二次 “去噪”相关系数矩阵，并采用阈值法构建全球股市网络模型，进而分析该网络拓扑结构特性和解释该网络中的风险传染效应。[7]（P144-152）吴翎燕发现基于 RMT 理论改进后的金融网络的拓扑性质更加明显，结构更加紧密。[8]孙雪莲基于RMT 理论，研究了相关矩阵“去噪”重构方法，提出一种新的“去噪”方法：“两点确定法”，并利用最小方差投资组合模型和均值-方差投资组合模型对比分析了去除“噪声”和未去除“噪声”对投资组合的有效前沿和风险预测的影响，证明了去除“噪声”可得到表现更优异的投资组合。[9]考虑到一个含有高质量信息的复杂网络对研究其拓扑性质的重要性，本文试图通过RMT 理论构造一个优化的股票市场网络模型，并对比分析优化前后网络稳定性及投资组合风险的差别。

二、研究设计

（一）样本及数据

上证180 指数选取规模较大、流动性较好且具有行业代表性的180 只股票作为样本构建指数，使其能够反映上海证券市场的概貌和运行状况。孙雪莲通过对不同采样频率的股票数据对比发现，在高频数据范围内，频率越高，相关矩阵所承载的信息量越大，在采样频率为120min 左右时，相关矩阵可以被看成是随机的。因此，剔除数据缺失天数较多的16 只股票，本文选取上证180 指数成分股比较活跃的164只股票2017年7月份的高频交易数据构建股票市场复杂网络模型，采样频率为5 分钟，采样指标为前复权收盘价。数据来源于WIND。

（二）数据处理

假设股票市场网络模型由n 只股票构成，Pit表示第i 只股票t日的收盘价，Pi,t-1表示第 i只股票t-1日的收盘价。由收盘价对应的对数收益率序列来求相关系数矩阵，对数收益率公式可表示为：

rit代表第i 只股票在t日的收益率。由收益率序列计算的各股票间的相关系数可表示为：

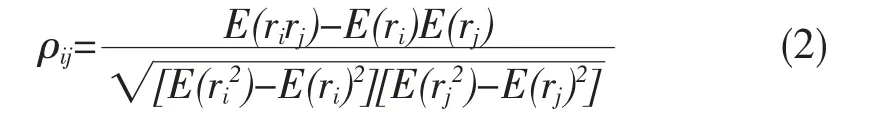
其中，用 E 表示数学期望，ρij表示 i 与 j 之间的相关系数，取值范围在-1 与1 间。一般地，若一个矩阵的所有元素非负并且每行元素和为1，则认为该矩阵是随机的，用公式可以表示为：

其中，A 是由M 个序列长度为N 的不相关的随机变量构成的M×N 矩阵，且每个序列都服从N(0,1)分布，即每行元素都服从均值为0、方差为1 的正态分布。定义Q=N/M，随机矩阵预测特征值的最大值和最小值可以表示为：

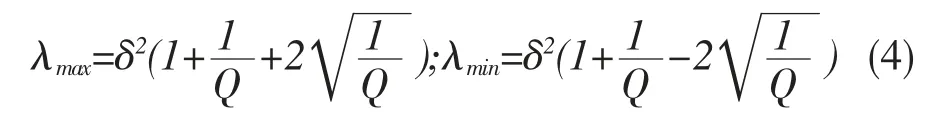
其中，λmax≥λ≥λmin，RMT 理论“去噪”的方法主要是通过处理相关系数矩阵和随机矩阵特征值来实现矩阵的优化。RMT 理论“去噪”主要包括LCPB、PG+和KR 三种方法，这三种方法各有优缺点，其中，PG+法是误差最小、“去噪”效果最好的一种方法。[11]（P589-606）本文将采取 PG+法对相关系数矩阵进行“去噪”处理。具体方法如下：

首先，谱分解相关系数矩阵C：

其中，P 为正交矩阵，PT为矩阵 P 的转置（PPT=1），Ω 为含有特征值的对角矩阵。将 Ω 矩阵中的特征值λ 从小到大排序得到特征值矩阵Ωs，具体形式为：

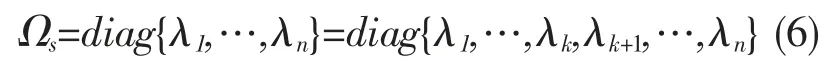
然后，以公式（5）预测出的随机矩阵最大特征值(λmax)为临界点，将特征值分为[λ1,λk]，[λk＋1,λn] 两个区间，其中，λk＜λmax＜λk＋1。PG+法认为RMT 预测范围内的特征值与随机矩阵特征值具有相同的属性，不能反映变量间的相互关系，该预测范围内特征值所包含的信息为 “噪声信息”，而小于RMT 预测范围的相关系数矩阵特征值所含有的信息很少，可以忽略不计。[10]PG+法“去噪”的思想是零值法，即将特征值小于λmax数值设置为0，即：

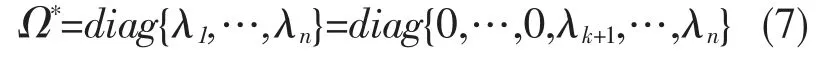
同时，相关系数的特征向量矩阵也保留了相同位置的特征向量（记为P*）。根据 Ω*和 P*，对相关系数矩阵重构：

其中，C*为新的相关系数矩阵，为了确保Tr(C)=Tr(C*)=n，新相关系数矩阵的主对角线元素设为1。

三、基于RMT理论的股票市场相关系数矩阵去噪

相关系数矩阵中含有的信息往往可以分为两类：一类是包含矩阵变量间相关关系的 “真实”信息；一类是干扰信息，也称为“噪声”信息。RMT 理论的目的就在于辨别出随机矩阵中的“干扰信息”和“真实信息”，通过对干扰信息的剔除来达到网络优化的目的。文章首先根据公式(3)构建一个与相关系数矩阵同维度的随机矩阵，对相关系数矩阵和随机矩阵的特征值分布进行对比分析。（见图1）从图中可以看出两矩阵的特征值有重叠部分，亦有差异部分，认为与随机矩阵特征值重叠部分的相关系数矩阵特征值所包含的信息具有随机性，将其作为“噪声信息”处理。

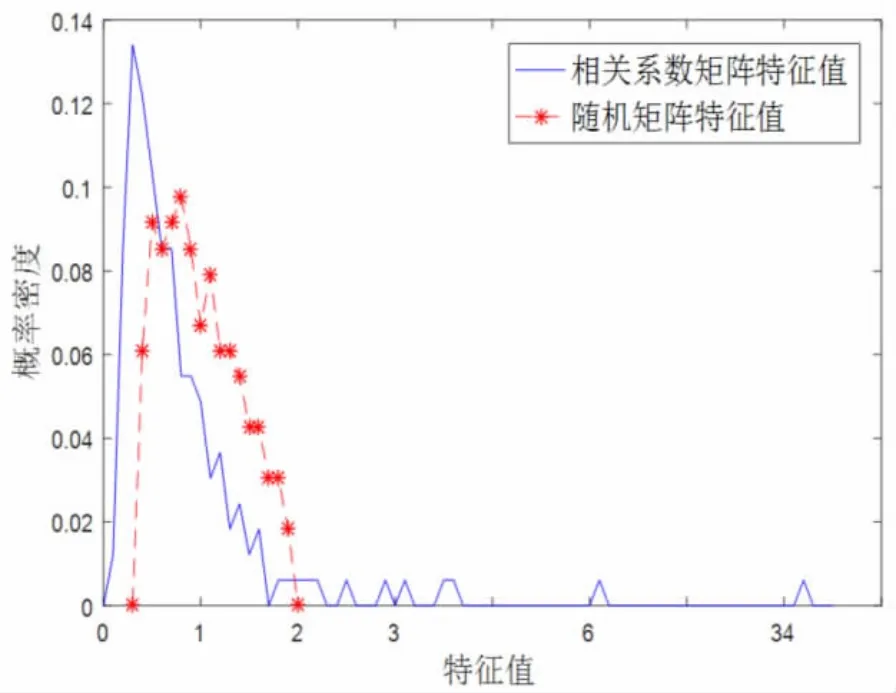
图1 相关系数矩阵和随机矩阵特征值分布图

文章将相关系数矩阵特征值、随机矩阵特征值和RMT 预测特征值进行了统计（见表1），可以看出，随机矩阵的特征值范围包含于RMT理论预测的特征值范围内，符合RMT 理论的预测原则。[11]（P589-606）而相关系数矩阵的特征值仅部分落在RMT 理论预测的特征值内。经统计，小于RMT 预测最大特征值的相关系数矩阵特征值共155 个，大于RMT 预测最大特征值的相关系数矩阵特征值共9 个。

矩阵特征值熵（记为SE）是用来评估特征值所含有信息量的有效工具，其熵值一般在[0,1]之间，SE 值越小说明其特征值所含信息具有更多的经济含义，反之亦然。为进一步确认偏离RMT 预测范围的相关系数矩阵特征值是否含有反映经济变量间关系的有效信息，文章用矩阵特征值熵分别来检验不同范围特征值所含信息对矩阵的影响。特征值熵(SE)的数学表达式可表示为：

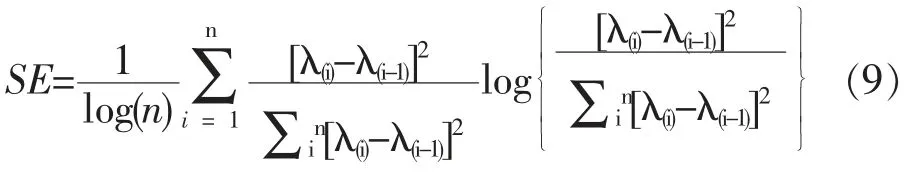
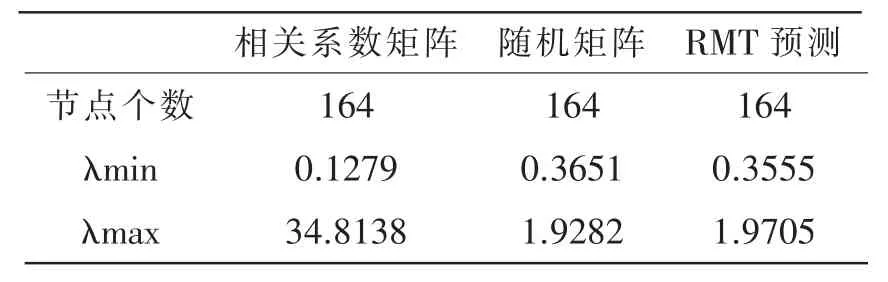
表1 各矩阵特征值的统计

本文通过公式(9)利用Matlab 软件对相关系数矩阵和随机矩阵的特征值熵进行统计。（见表2）从表中可以看出相关系数矩阵中含有大量代表经济含义的有效信息，而随机矩阵所含信息量很少。当去除最大的9 个特征值时，相关系数矩阵的特征值熵骤升，说明剔除较大的特征值会降低相关系数矩阵所含信息的有效性。当去除随机矩阵最小的155 个特征值时，随机矩阵特征值熵不增反减，意味着该部分特征值的剔除增加了随机矩阵的经济信息含量，正体现出RMT 理论“去噪”的效果。

表2 矩阵特征值熵统计

因此，本文通过剔除相关系数矩阵小于RMT 预测的最大特征值的那部分矩阵特征值来对相关系数矩阵“去噪”处理。具体做法如下：首先，以上证180 指数成分股高频交易数据对应的对数收益率序列为基础，由公式(2)计算出相关系数矩阵，根据RMT 理论“去噪”原理，通过公式(3)构建一个与相关系数矩阵同维度的随机矩阵。其次，由公式(5)对相关系数矩阵进行谱分解之后根据PG+法步骤剔除信息含量很少的特征值及其对应的特征向量。最后，根据公式(8)重构“去噪”后的相关系数矩阵。

四、实证分析

（一）网络模型的构建

文章以股票市场中各股票为节点，股票相关性为连边，根据阈值法构建股票市场复杂网络模型。文章根据原网络相关系数矩阵随着阈值增加，最大连通子图和第二大连通子图所含节点个数的变化情况确定阈值，将阈值确定为0.28。[12]（P249-253）根据阈值法理论，认为相关系数大于0.28 的节点间有连边在相关系数矩阵中记为1，相关系数小于0.28 的节点间没有连边在相关系数矩阵中记为0。将相关系数矩阵转换为只含有0、1 元素的邻接矩阵，由邻接矩阵构建无权无向的股票市场复杂网络模型。为保证网络优化前后的可比性，以优化后的相关系数矩阵建立阈值为0.28 的优化网络。本文使用Pajek 软件构建网络模型。

（二）网络优化前后的稳定性分析

复杂网络模型在遭受到外部有意或者无意的攻击时具有一定的稳定性，这种稳定性在实际股票市场中可理解为，当外部经济受挫时，股票市场维持其自身运行的能力。稳定性越高的网络模型其所代表的实体市场抗风险性越强。将网络中所有节点在不同路径长度下的闭合路径数量总和定义为子图中心性（记为Sc），该指标体现了网络的连通性。依次剔除从大到小排序的节点度，对网络进行蓄意攻击，观察随着移除节点数目的增加，网络优化前后Sc 值的变化情况。如图2所示，随着移除节点数目的增加，原网络与优化网络的Sc 指标均呈下降趋势，说明无论网络是否优化，节点移除数目的增加都会导致网络连通性的下降。当移除度值大的Hub 节点时，对网络有较强的攻击性，原网络Sc指标与优化网络Sc 指标以近似相同的速率在优化网络Sc 指标下方递减，此时网络连通性快速下降；随着节点移除数目的增加，所移除节点对网络的重要性下降，攻击性减弱，原网络和优化网络Sc 指标下降速度减缓，最后以相同的速度缓慢递减。当所剔除节点为网络Hub 节点时，蓄意攻击下优化后网络的Sc 运动曲线始终在原网络Sc 运动曲线的上方，说明优化后的网络结构更稳定。

图2 随着节点移除数目的增加，Sc 指标变化情况

（三）网络优化前后投资组合风险分析

1.预期收益下的风险对比

马科维茨投资组合模型为多目标优化问题（即风险一定，收益最大；收益一定，风险最小），以预期收益率期望度量收益（回报率）；以收益率方差度量风险。考虑允许卖空情况下的投资组合，具体模型如下：

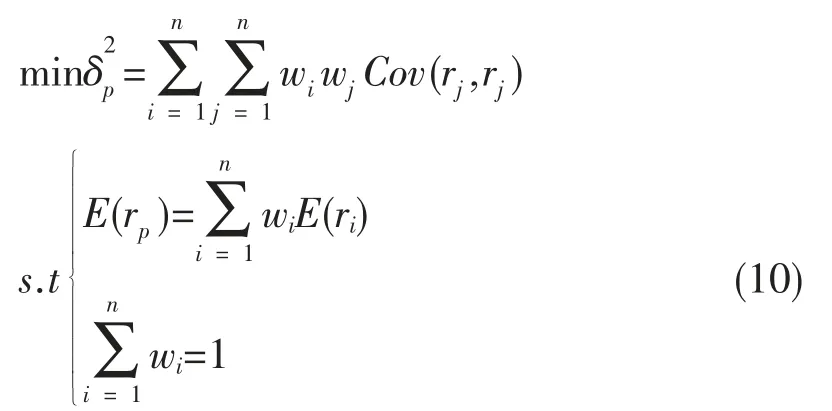
其中，E(rp)为期望收益率，ri、rj为第 i 种和第 j 种资产的收益，wi、wj为资产 i 和资产 j 在组合中的权重，δp2为投资收益的方差即组合的总体风险，Cov(ri,rj)为两种资产的协方差。通过调节参数E(rp)求解投资组合的有效边界。根据马科维茨模型的假设，将收益率序列平分成两个时期，根据第一期的收益率计算预测风险和收益，根据第二期的收益率计算实际风险和收益。这里定义由第二期的回报率和第一期的相关矩阵计算得到的有效前沿称为预测的投资组合，对应的风险称为预测风险；用同样的投资组合，但用第二期的相关矩阵计算在相同回报率情况下该组合的风险称作实际风险。根据上述风险和收益计算方法，以及相关系数矩阵与协方差矩阵的变换关系，RMT 理论“去噪”前后的预测风险和实际风险可用如下模型表示，其中δ2为方差，W=(w1,w2,…,wn)，Cov 为协方差矩阵，σ 为对角矩阵其主对角元素为相关矩阵的标准差，C为相关系数矩阵，1、2 分别指第一期、第二期。

“去噪”前预测风险：δa2=WCov1WT=W(σ1C1σ1)WT;

“去噪”前实际风险：δb2=WCov2WT=W(σ2C2σ2)WT;

“去噪”后预测风险：δa2'=W'Cov1'WT'=W'(σ1'C1'σ1')WT';

“去噪”后实际风险：δb2'=W'Cov2'WT'=W'(σ2'C2'σ2')WT'。

实际风险收益曲线和预测风险收益曲线（见图3），可以看出，在收益相等时，“去噪”后的预测风险高于“去噪”前预测风险，而“去噪”后的实际风险低于“去噪”前的实际风险。也就是说，“去噪”前的风险被低估，用该投资组合进行实际投资时实际风险比较大，RMT 方法改进之后，相对准确地估计了风险，可减少在实际投资时的风险，降低实际投资损失。尤其是对追求高风险高收益的投资者来说，在高风险高收益时相同收益下，优化后的实际风险显著低于优化前的实际风险，更有利于投资者进行风险规避。

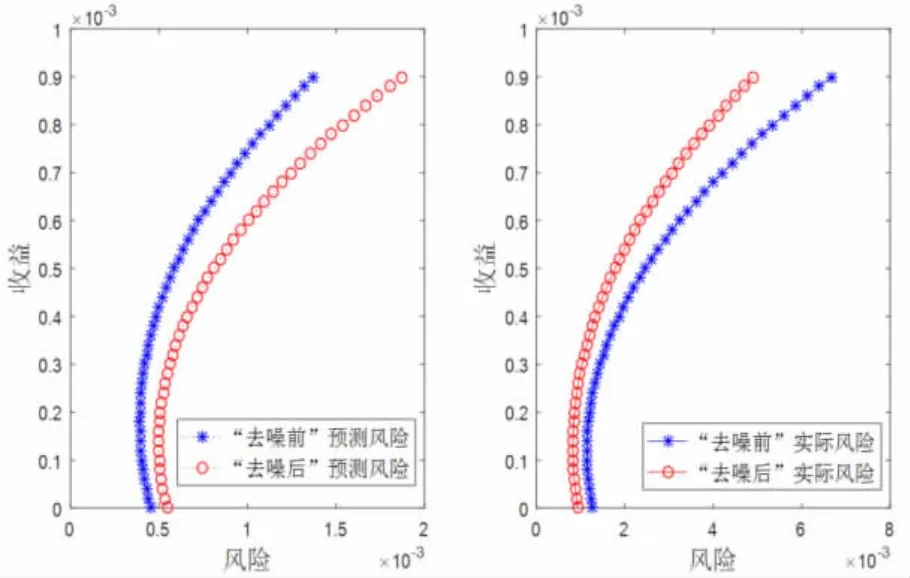
图3 实际风险收益曲线和预测风险收益曲线

2.预测准确性比较

表3 实际风险与预测风险的差异系数

总之，本文将RMT 理论运用到我国股票市场复杂网络模型中，以去除网络模型中的噪声信息来对网络模型进行优化，并对股票市场复杂网络模型“去噪”前后的效果进行分析。我们以上证180 指数成分股5 分钟高频交易数据为研究对象，对比分析了股票市场相关系数矩阵与同维随机矩阵特征值分布特性，发现随机矩阵特征值全部落在特征值预测范围内，而相关系数矩阵特征值仅部分落在特征值预测范围内。使用特征值熵指标分区域对特征值所包含的经济信息进行判断，发现小于最大预测特征值部分的特征值所包含的信息降低了信息的有效性。据此我们根据随机矩阵理论对股票市场复杂网络模型进行“去噪”处理，得到新的更适于建立复杂网络模型的相关系数矩阵，并根据阈值法构建当阈值为0.28 时的优化后的网络模型。在此基础上，文章通过蓄意攻击分析了网络优化前后稳定性的不同；通过投资组合风险对比分析了网络优化前后预测风险和实际风险的异同。实证分析结果表明，当市场相对稳定时，相比原网络，RMT 理论优化后的网络不仅可以提高网络的稳健性,而且还降低了实际投资组合中的风险。