三组谱的Sturm-Liouville反问题

刘瑶

(陕西师范大学数学与信息科学学院,陕西 西安 710119)

1 引言

考虑定义在L2[0,a]上的四组Sturm-Liouville问题:D-D问题

R-D问题

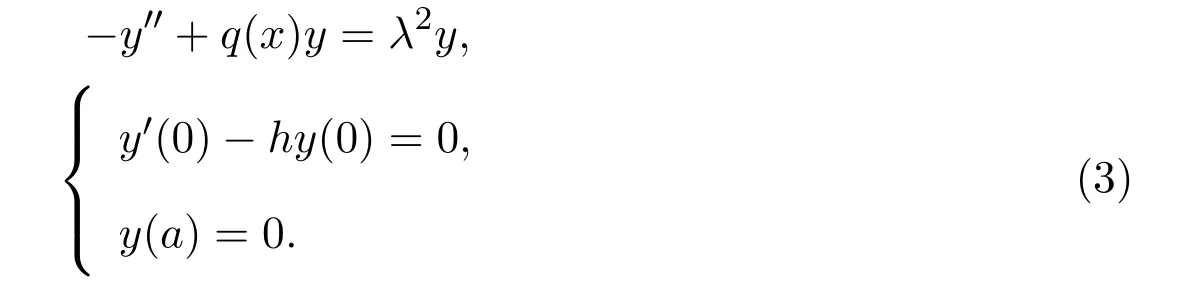
D-R问题

R-R问题

其谱分别记作

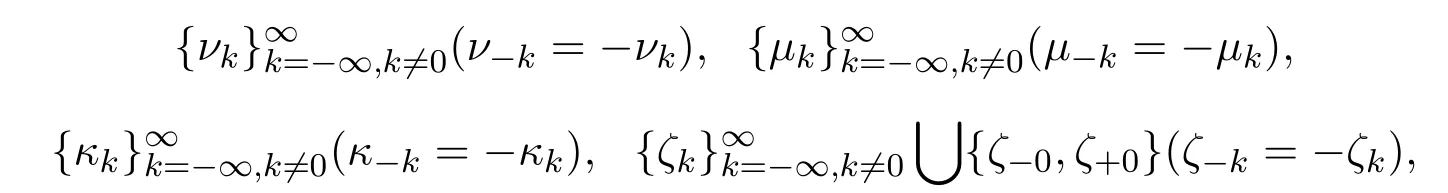
其中q(x)∈L2[0,a]为实值函数,h∈R为一固定的常数,由文献[1-2]可知它的谱是简单的无界的.

Sturm-Liouville算子的逆问题,特别是关于势函数q(x)的唯一确定性问题,长期以来受到数学和物理学界的关注,并产生了许多的研究成果.Brog[3]于1946年首先提出并证明了通过两组特征值可得到Sturm-Liouville微分算子势函数q(x)的唯一确定性.Levitan[3]和Marchenko[3]分别证明了一组特征值及其对应的规范常数同样能唯一确定势函数q(x).如果边界条件中的常数是给定的,那么重构势函数就不需要完整的两组特征值,这一问题有时称为”缺少特征值问题”,即通过部分特征值唯一确定未知区间的势函数(见文献[4-5]).

文献[2]证明了四组谱定理,即对于给定的两组数列,在一定条件下可划分为四组数列,使其分别成为D-D,D-N,N-D,N-N四个Sturm-Liouvile问题的部分特征值,最后通过四组谱的部分特征值唯一确定了整区间上的势函数q(x).同样的方法也在文献[6-7]中用于解决相关的反问题.

本文的目的在于,将Neumann边界条件推广到Robin边界条件,上述结论依然成立.换言之,将给定的两组数列在一定条件下划分成三组数列,使其分别成为D-D,R-D,R-R三个Sturm-Liouville问题的部分特征值,并通过三组谱的部分特征值唯一确定区间[0,a]上的的势函数q(x),再由Gelfand-Levitan方程给出区间[0,a]上势函数q(x)的重构公式.

2 预备知识

首先给出四组Sturm-Liouville问题的特征函数和特征值的渐近式,为本文结论的证明提供必要的准备.

定义φi(x,λ)(i=1,2)为(1)的解,分别满足下列初始条件

根据文献[8-11]可得

利用分部积分法则有

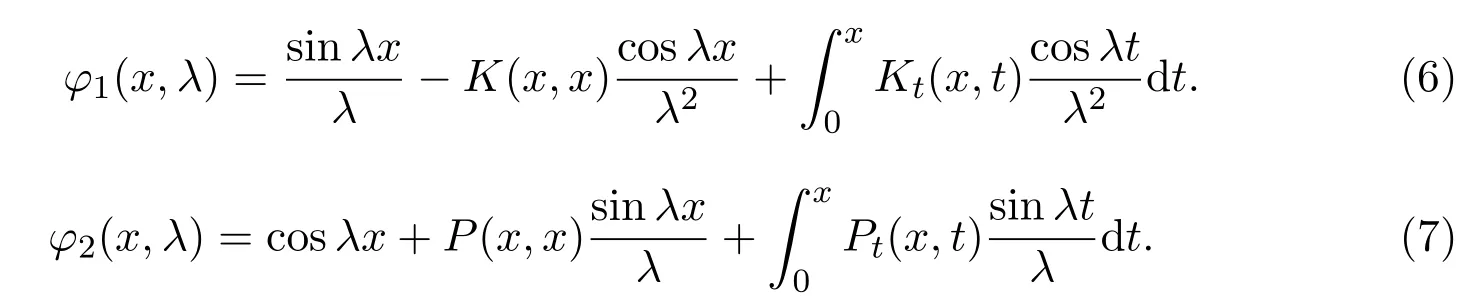
对上述两式求导

由 (6)式-(9)式可得

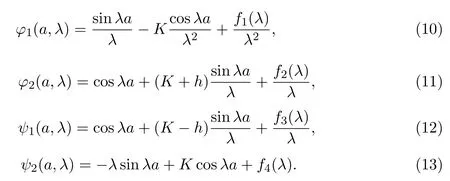
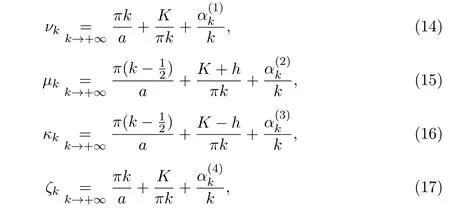
令ω(λ)=φ1(x,λ)ψ2(x,λ)−ψ1(x,λ)φ2(x,λ),由文献 [12-13]可知ω(λ) 与x无关,且恒等于−1.

定义 2.1[14]若函数f(x)满足以下三个条件

(i)指数阶为a的整函数;

(ii)函数的所有零点是单重的;

(iii)若存在正数L,M以及p>0,则

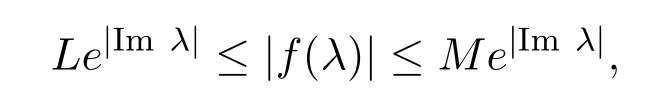
其中|Imλ|≥p,则称f(x)为sine型函数.

3 主要结论及其证明

本节给出主要结论,即通过将给定的两组数列划分为三组数列,使其分别为D-D,R-D,R-R三个Sturm-Liouville问题的部分特征值,由三组部分特征值唯一确定区间上[0,a]的势函数q(x),最后通过Gelfand-Levitan方程给出区间[0,a]上势函数q(x)的重构公式.

定理 3.1设三组数列满足,且有如下的交替性

这里{rj}j∈A1⊂N,{sj}j∈A2⊂N为自然数数列,满足,A是实常数,则存在唯一势函数q(x)∈L2[0,a],使得{νrj},{µk}和{ζsj}分别是问题 (1),(2),(1),(3)和 (1),(5)的特征值.

证明由 Borg两组谱定理 (见文献 [1])可知满足交替性和渐近式,则存在唯一的势函数(x)∈L2[0,a],使得分别是问题(1),问题(2)和问题(1),问题(3)的特征值,现在需要找到由(x)生成的问题(1),问题(4)和问题(1),问题(5)的特征值.

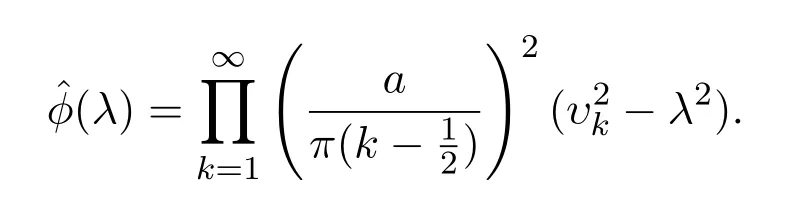
由文献[10]可得

这里定义A=B−h.由构造函数

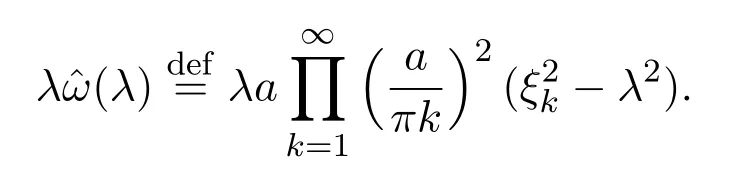
由 sine型函数定义知λω(λ)是sine型函数,由文献 [10]则有

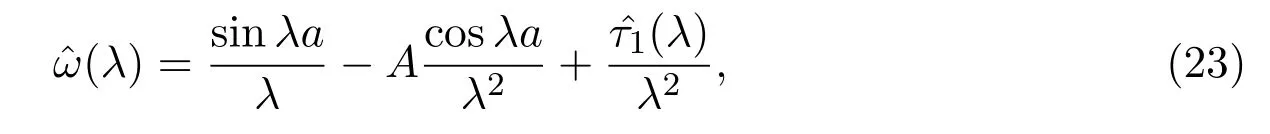
为节点处的函数值,结合(22)式有

结合(20)式,利用三角函数的泰勒展式有

因此,由文献[14]中的定理A(也可见文献[15])可得上式的拉格朗日插值级数为

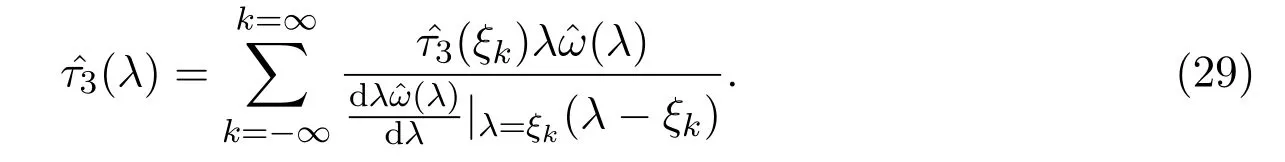
上式右边的级数在复平面C的任一紧子集上一致收敛,按实数λ的L2(−∞,+∞)的范数收敛于一个属于La的函数.根据文献[14]构造的是下面插值问题的唯一解:给定插值节点和节点处的函数值,构造函数.令

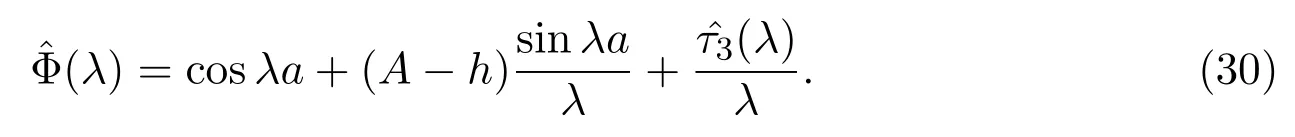
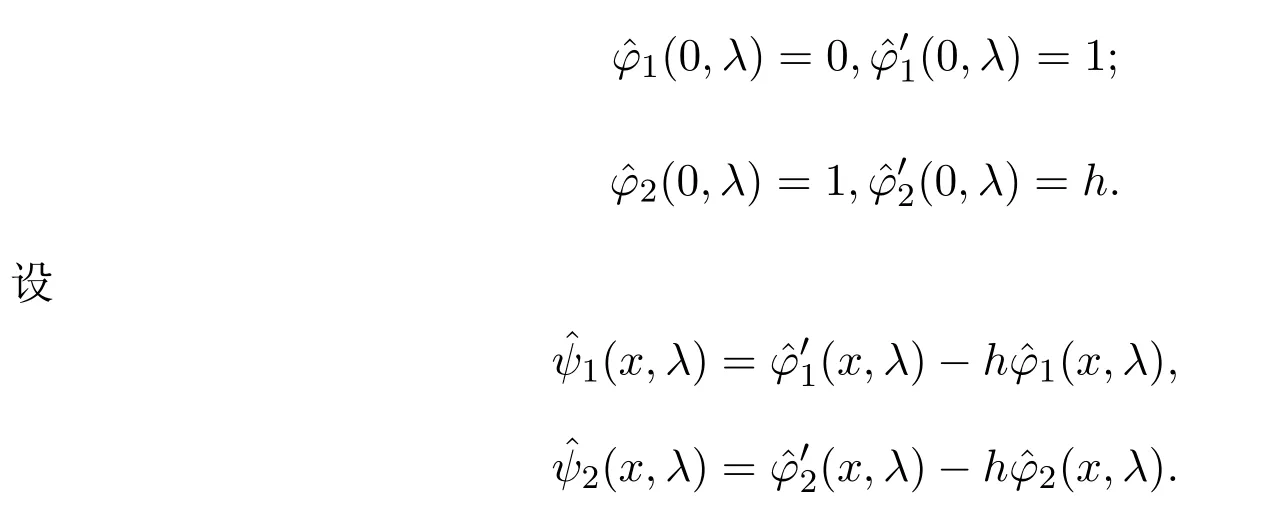
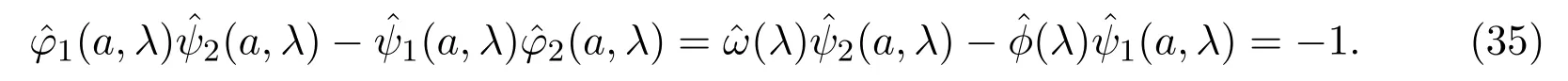
结合(32)式可得

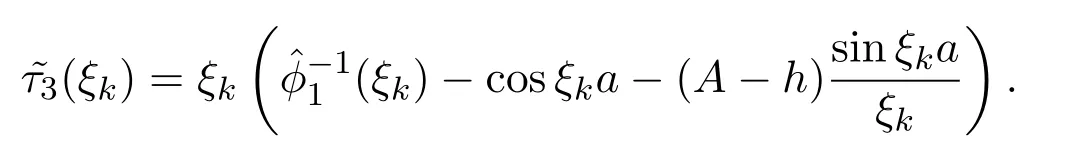
结合(16)式

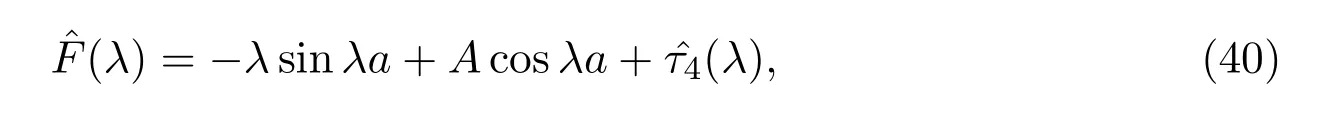
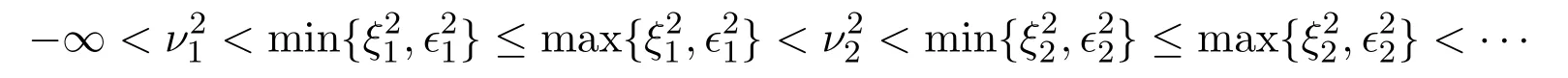
按照如下的形式划分数列中的元素

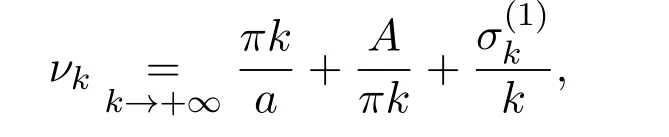
令

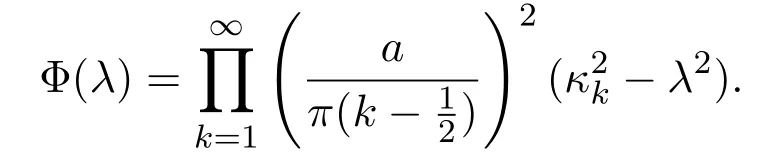
由文献 [10]可知ω(λ),ϕ(λ),Φ(λ)的表达式为

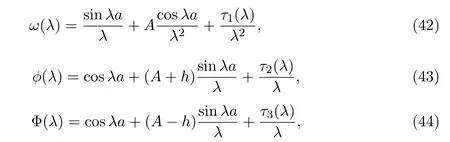
其中τi∈La,i=1,2,3.如果φi(x,λ),i=1,2是方程 (1)的解,那么φ1(a,λ)=ω(λ),φ2(a,λ)=ϕ(λ),ψ1(a,λ)=Φ(λ),这表明φ1(a,νk)=0,k∈{rj},φ2(a,µk)=0,k∈N和ψ1(a,κk)=0,k∈N,接下来需要证明ψ2(a,ζk)=0,k∈{sj}.令

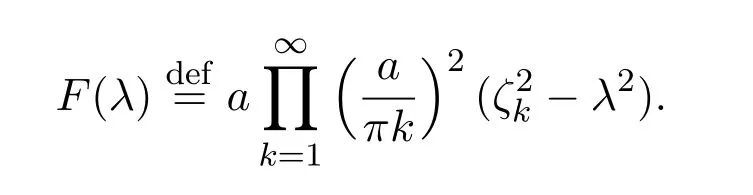
由文献[10]可知表达式为

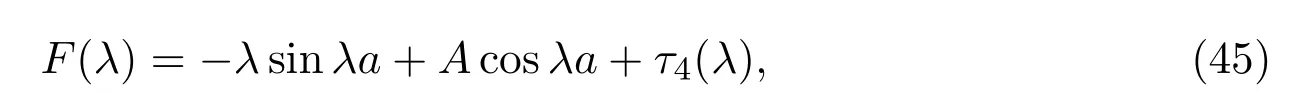
其中τ4∈La.从定义可得,这表明ω(λ)F(λ)的零点集和(λ)(λ)的零点集相同.由(23)式,(39)式,(42)式和(45)式则有

通过定义可知

即ϕ(λ)Φ(λ)的零点集和(λ)(λ)的零点集相同.结合(22)式,(30)式,(43)式和(44)式可得

将 (37)式和 (39)式代入(35)式,结合(46)式-(47)式得到

另一方面,由于

有唯一解,则有F(λ)≡ ψ2(a,λ),从而ψ2(a,ζk)=0,k∈{sj}.定理证毕.

下面给出势函数q(x)的重构方法(文献[1]),概括如下:

(b)由αk=−(νk)ϕ(νk),其中,计算可得αk.

(c)通过{αk,µk}k≥0构造函数

(d)解Gelfand-Levitan方程

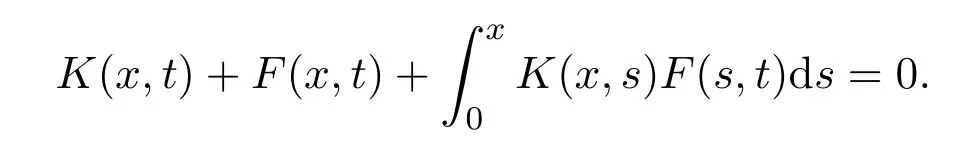
注意到上式是一个Fredholm积分型方程,因此有唯一解K(x,t),从而

致谢:导师魏广生教授对本文作了重要指导,提出了宝贵意见,作者在此表示衷心感谢.