基于LOF的K-means聚类方法及其在微震监测中的应用*
刘德彪,李夕兵,李 响,尚雪义
(中南大学 资源与安全工程学院,湖南 长沙 410083)
0 引言
微震监测技术在深部开采的矿山中,得到了越来越广泛的应用[1-4]。微震事件数目庞大,其区域分布特征人工划分具有较大的主观性。聚类分析借助聚类算法实现微震事件的划分,可降低人工划分的主观性,发现潜在的微震集群,从而有效的分析微震事件分布特征和活动规律。
目前,国外学者对地震事件聚类分析进行了较多研究,且在国内也越来越受到关注。Zaliapin等[5]采用K-means对人为和地质构造引起的地震事件进行了区分;Weatherill和Burton[6]采用K-means证明了震源模型可由地震目录信息计算得到;Morales等[7]提出1种基于自适应马氏距离的K-means聚类方法,该方法可用于球形簇和椭球形簇地震聚类;Ramdani等[8]将地震深度属性引入到K-means聚类分析,改善了地震事件动态变化过程的图像分辨率;吴爱祥等[9]用最短距离聚类法分析了矿山微震活动的时空分布,区分了矿山的微震聚集区;Wang等[10]采用模糊C均值聚类得出了微震事件的活动特征与三维波速之间的关系;Shang等[11]提出采用S-KL指标选择最佳聚类数,并解释了聚类簇与地质构造的关系;刘栋等[12-13]采用时空共享近邻聚类算法(STSNN)和具有噪声的基于密度的聚类方法(DBSCAN)分析了岩体的活动性。
由上述分析可知,在地震聚类分析中K-means运用最为广泛。K-means聚类算法具有较高的计算效率和较强的灵活性,适用于球形簇结构的数据集,但数据集中的异常事件会对算法的结果产生较大的影响。初始聚类中心的选择也容易影响聚类结果,使得聚类算法很难达到全局最优值。Wang等[14]提出了1种改进的K-means聚类算法,先用基于局部离群因子(Local Outlier Factor,LOF)的方法检测异常并移除事件,然后用所有数据的均值作为第1个初始聚类中心,再依次计算其他的初始聚类中心,该方法提高了聚类的准确性。
本文借鉴Wang等[14]提出的算法,提出了1种新的基于LOF的K-means聚类算法(LOF-K-means),并用该方法对矿山微震事件的分布特征进行分析。首先,采用LOF检测离群微震事件和选取初始聚类中心,再利用Krzanowski-Lai(KL)指标确定最佳聚类分组数。采用簇内误差平方和(within-cluster Sum of Squared Errors, SSE)比较本文方法、文献[14] K-means聚类方法和传统K-means聚类的聚类效果。最后,采用本文方法对用沙坝矿微震事件进行聚类分析,根据聚类簇的分布特征对矿山的微震活动性作出评价。
1 局部离群因子算法
局部离群因子算法[15]是1种基于密度来进行异常事件检测的算法。局部离群因子的大小反映对象xi对于局部中心的偏离程度,局部离群因子的值越大,说明对象xi偏离局部中心的程度越多,所在位置局部密度越小;局部离群因子的值越小,说明对象xi偏离局部中心的程度越少,所在位置局部密度越大,越接近局部中心。在本文中,用dist(xi,p)表示对象xi与对象p之间的距离,局部离群因子LOFk(xi)的具体定义如下:
定义1:对象p的第k距离k-dist(p)在数据集X中,若满足:
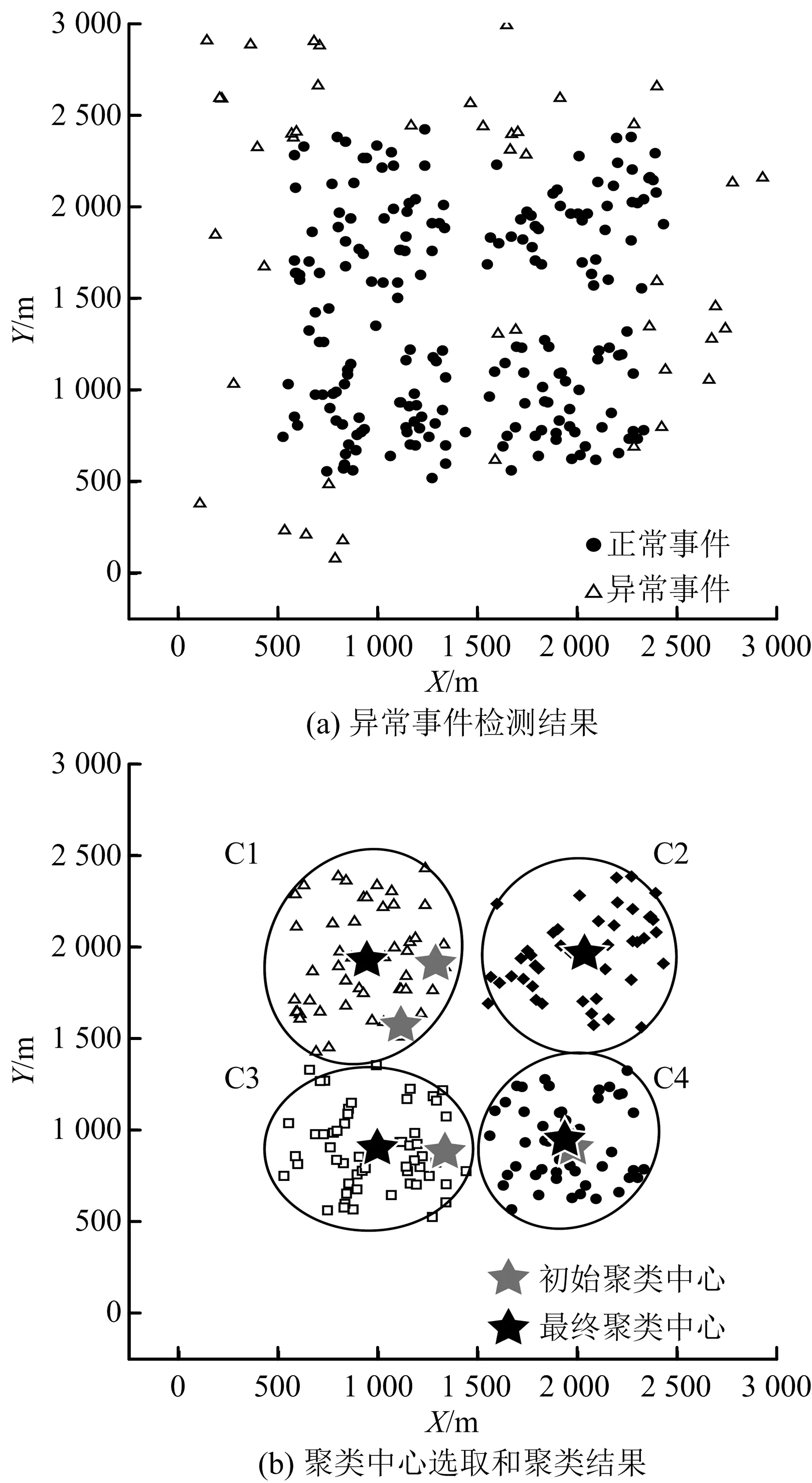
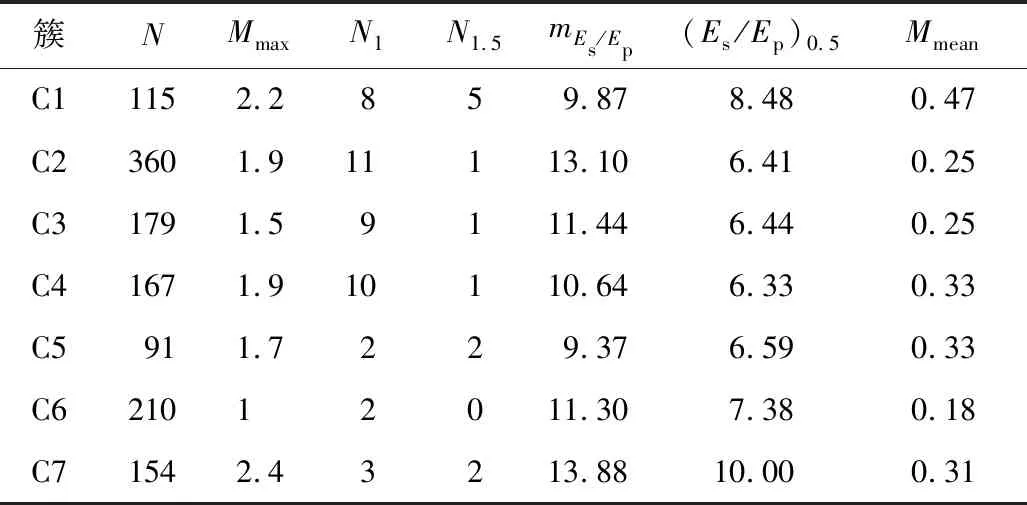
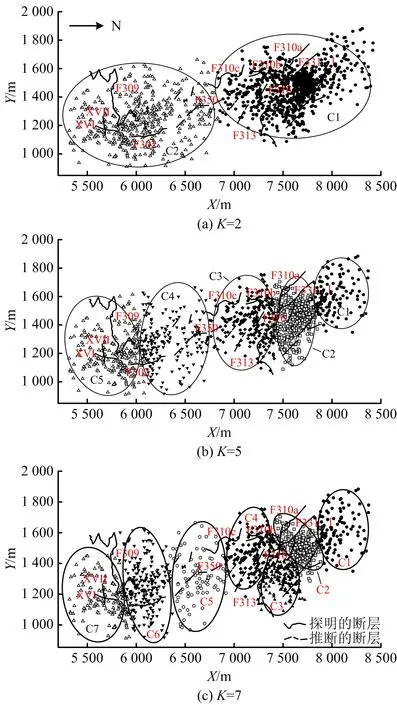
1)存在至多k-1 个对象xi′∈X(xi′≠xi)且dist(xi′,p) 2)存在至少k个对象xi′∈X(xi′≠xi)且dist(xi′,p)≤dist(xi,p),则对象p的第k距离记为k-dist(p)=dist(xi,p)。图1说明了k=6时,对象p1的第k距离k-dist(p1)。 图1 k=6时的第k距离领域与可达距离Fig.1 k-distance neighbourhood and reachability distance, when k=6 定义2:对象p的第k距离领域Nk(p) Nk(p)指对象p的第k距离内所有对象组成的集合(包括第k距离)。|Nk(p)|是指对象p的第k距离领域内所有对象的个数,且|Nk(p)|≥k。图1对象p1的|Nk(p1)|为7,对象p2的|Nk(p2)|为6。 定义3:对象xi相对于对象p的可达距离 令k为正整数,对象xi相对于对象p的可达距离计算如下: reach-distk(xi,p)=max(k-dist(p),dist(xi,p)) (1) 图1中,对象xi相对于对象p1的可达距离为reach-distk(xi,p1)=k-dist(p1),对象xi相对于p2的可达距离为reach-distk(xi,p2)=dist(xi,p2)。 定义4:对象xi的局部离群因子 对象xi的局部离群因子LOFk(xi)的定义如下: (2) 式中:lrdk(xi)是指对象xi的局部可达密度(Local Reachability Density),定义如下: (3) 由公式(2)~(3)可知,对象xi的LOF值越小,说明其局部可达密度越大,越接近局部中心;对象xi的LOF值越大,说明其局部可达密度越小,越接近局部边缘,为异常事件的可能性越大。 数据集中的异常事件容易影响K-means聚类结果,因此聚类前需检测和剔除异常事件。首先,利用公式(2)计算数据集X中每个对象xi的LOF值,再将所有对象xi的LOF值按升序排列,并进行归一化处理;然后,将所有对象xi的归一化值进行升序排序,并计算出其拐点值,将此值作为异常事件和正常事件的临界值[16]。如果对象xi的归一化值大于拐点值,则剔除对象xi;反之,则留下对象xi。高斯分布的归一化公式如下[17]: (4) 本文选取初始聚类中心的思路为:选择去除异常事件数据集中,LOF值最小的对象xi作为聚类算法的第1个初始聚类中心;然后,将与第1个初始聚类中心距离较远且全局密度较大的对象作为第2个初始聚类中心;接着,将与前2个初始聚类中心的均值相距较远且全局密度较大的对象作为下1个初始聚类中心,直到计算得到与聚类分组数相同的聚类中心数为止。具体如下: 2)计算第2个初始聚类中心,直到第K个初始聚类中心。 (5) LOF-K-means聚类算法实现过程如下: Input:数据集X={x1,x2,…,xn},聚类分组数K,第k领域值k。 Step2:用2.1.2节的方法选取初始聚类中心。 LOF-K-means聚类算法采用拐点值判别异常事件,较人为判别更加客观。同时,用LOF值最小的对象,即所在区域密度最大的对象作为第1个聚类中心,可以适应更广泛类型的数据集,避免出现数据集类型或者大小的改变对聚类算法产生的影响。 1)聚类效果评价 采用函数簇内误差平方和(within-cluster Sum of Squared Errors, SSE)评价聚类效果,SSE值越小说明各类间分隔越明显,聚类结果越好。 (6) 2)聚类数选取指标 采用KL指标确定聚类数,Krzanowski和Lai[18]通过计算2个连续不同分组数的聚类结果的簇内协方差矩阵的迹来确定最佳聚类分组数。KL指数值越高,其对应分组数的聚类结果越好。对于聚类分组数K≥2的数据集X={x1,x2,…,xn},xi∈Rd,KL指标的定义如下: (7) 为测试本文方法的优越性,选取传统K-means聚类和文献[14] K-means聚类算法作为对比。不同聚类方法的聚类效果可能受数据集的大小影响,本文选取数据集包含100,250,500,750和1 000个对象进行讨论。同一数据集分别运用上述3种聚类算法进行聚类计算,使用的聚类参数为x, y轴坐标,第k领域设为20。首先计算上述3种聚类方法在同一数据集、同一个分组数下的SSE值,SSE值由小至大分别记为①,②和③,根据表1进行比较得到评分,见表1。例如:LOF-K-means聚类、传统K-means聚类和文献[14] K-means聚类算法的SSE值分别为100,200和150时,那么该SSE值由小至大排列后,对应表1中的评价工况4,且LOF-K-means聚类、传统K-means聚类和文献[14] K-means聚类算法评分分别为2,0和1。再将每1种聚类算法在2~10个聚类分组下得到的评分相加,得到总评分作为该聚类算法的综合SSE评价指标,其值越大则说明该聚类算法越好。为减少个别聚类结果对不同聚类方法的影响,将每种数量规模的数据集分别随机生成100次进行聚类计算,得到这3种聚类方法的综合SSE评分。图2为数据的聚类过程。可知初始聚类中心的选取与数据集的分布有关,且与数据集的局部密度紧密联系。 表1 不同SSE工况下评分Table 1 Scoring for different SSE conditions 注:①~③分别对应SSE值从小到大排列的3种聚类方法。 图2 数据集的聚类过程Fig.2 Clustering process of dataset 模拟测试的结果如图3所示,当数据集事件数为100,250和1 000时,LOF-K-means聚类综合SSE评分的中位数最大;当事件数为500和750时,其中位数与文献[14] K-means聚类的相同,上四位数与文献[14] K-means聚类的相同或较大,两者均比传统K-means聚类的评分大。 图3 不同数据集大小的聚类结果Fig.3 Clustering results for different sizes of dataset 总的来说,对于不同事件数大小的数据集,LOF-K-means聚类算法的聚类效果最好,文献[14] 的聚类方法次之,传统K-means聚类方法效果最差。 本文实例所用的数据来源于用沙坝矿微震监测系统,其位于贵州省中部,东经106.81°,北纬27.08°。矿体呈稳定的层状,矿体厚度稳定,沿走向和倾向连续性较好,倾角为10°~55°,磷矿的年产量超过200万t且已探明的矿石储量为4 000多万t。2013年开始,在用沙坝矿区建立了矿山IMS微震监测系统,主要用来监测矿区内的微震活动。IMS微震监测系统由28个传感器组成 ,如图4(a)中三角形区域,其中单向传感器有26个,三向传感器有2个;主要分布在920中段,1080中段和1120中段。图4(a)说明矿山微震事件主要分布在巷道区域,图4(b)为矿山生产活动区域和断层分布,可知微震事件分布与生产活动区域和断层分布具有较好的吻合性。一般认为较大震级微震主要受断层影响,本文选取了较大震级的事件(M≥0)展开分析[11],尝试将微震事件与断层活动联系起来。 图4 用沙坝矿区的微震系统与断层分布Fig.4 Microseismic system and fault distribution in Yongshaba mine 本文使用的数据集为2014年1-6月测得的1 649个矩震级大于等于0级的微震事件,如图4(a)中圆形所示。采用LOF-K-means聚类算法,使用的聚类参数为微震事件的x,y,z轴坐标,所取的第k领域为k=90。聚类后的KL指数如图5所示,可知较好的聚类分组数为2,5和7。 图5 LOF-K-means聚类的微震事件KL指数Fig.5 KL index of microseismic events by LOF-K-means clustering 图6给出了聚类分组数K为2,5和7的微震事件聚类结果,参照文献[11],选取的一些重要聚类参数值见表2~4。从图6(a)可知,K=2时,矿区的微震事件由断层F310c和断层F350划分为左右两簇。分析可知,C1簇主要受主断层F310,F313和断层F316,F331的影响;C2簇主要受主断层F309,F350和F302的影响。结合表2,可以解释这2个聚类簇主要依据区域断层结构间的作用,而引起微震事件的影响程度进行划分。C1簇和C2簇的mEs /Ep值大于10,且C2簇的(Es/Ep)0.5为8.07比C1簇的大,说明C2簇受断层的影响更大。 表2 K=2时,不同聚类簇的微震参数Table 2 Microseismic parameter of different clusters,when K=2 表3 K=5时,不同聚类簇的微震参数Table 3 Microseismic parameter of different clusters,when K=5 表4 K=7时,不同聚类簇的微震参数Table 4 Microseismic parameter of different clusters,when K=7 注:N指簇内微震事件数;Mmax指簇内最大的震级;N1指簇内震级≥1.0的微震事件数;N1.5指簇内震级≥1.5的微震事件数;mEs/Ep为簇内S波与P波能量比的均值;(Es/Ep)0.5为簇内S波与P波能量比的中位数;Mmean为簇内平均震级。 图6 用沙坝矿微震事件LOF-K-means的聚类结果Fig.6 LOF-K-means clustering results of microseismic events in Yongshaba mine 从图6(b)可知,K=5时,C1簇受断层I的影响,C2簇和C3簇沿着主断层F310a,F316和F313划分;C4簇受主断层F350和F302影响;C5簇受主断层F309和断层XVII,XVI的影响。结合表3,C1簇的事件数最少,但N1.5有5个;mEs/Ep大于10,(Es/Ep)0.5与其他簇相比处于较大值且Mmean最大,说明C1簇主要受断层滑移的剪切作用影响,推测主断层F310或F331可能延伸到C1簇区域。C2簇的事件数最多,mEs/Ep大于10,N1有18个,N1.5有2个,说明其受到断层滑移的影响;但Mmean最小且(Es/Ep)0.5较小,说明其也受到矿山生产活动的影响,且影响作用比断层滑移的大。C3簇与C2簇类似,受到矿山生产活动和断层滑移共同影响。C4簇与C5簇所在区域较难描述,但C5簇mEs/Ep大于10且(Es/Ep)0.5接近10,说明其基本受断层滑移的剪切作用影响。 从图6(c)可知,K=7时,C1簇与K=5时的C1簇基本相同,C2簇主要受主断层F310a和F331的影响,C3簇与C4簇沿着主断层F313和F316划分;C5簇受主断层F350的影响;C6簇受主断层F302的影响且沿着F309与C7簇划分。C2 簇与C3簇的各项微震参数基本相同,且与K=5时的C2簇相似,说明主要受到各断层滑移和矿山生产活动共同影响。C4簇与C3簇类似,但Mmax和Mmean较大,说明其受到各断层滑移和矿山生产活动共同影响,相对受断层滑移的影响程度较大。C5簇的事件数较少但N1.5有2个,且mEs/Ep和(Es/Ep)0.5都大于3不到10,说明该区域由断层滑移和矿山生产活动共同作用;且从微震事件数量上看,矿山生产的影响较小,断层滑移的影响较大。C6簇可作为由矿山生产造成微震事件典型的集群,事件数较多且Mmean和Mmax最小,说明其由矿山生产活动影响,虽然其mEs/Ep和(Es/Ep)0.5均大于3,但综合分析仍可认为C6簇主要处于矿山生产活跃区域。C7簇mEs/Ep和(Es/Ep)0.5均大于10,N1.5有2个,Mmean为0.31,说明主要受断层滑移剪切作用的影响。总的来说,K=7时各簇微震事件的分布效果较好,可以更好的解释微震活动性特征。 K=7时聚类簇事件的时钟矢量图如图7所示。由图7可知,C1,C5和C6簇微震事件初期发生时间集中在12∶00方向,后逐渐转向13∶00~14∶00;C2,C3,C4和C7簇微震事件发生时间主要在13∶00~14∶00。7个聚类簇微震事件的轨迹曲线都超出圆,说明矿区微震事件受生产活动影响。用沙坝矿区的生产爆破时间集中在11∶00~13∶00,则爆破期间和爆破后的1~3 h内是微震事件频发期。 图7 K=7时聚类簇事件的时钟矢量Fig.7 Clock vectors of clustering events ,when K=7 1)针对K-means聚类易受异常事件和初始聚类中心影响的问题,引入了LOF算法进行异常事件的检验和初始聚类中心的选择,提高了聚类结果的有效性。 2)建立了聚类算法的综合SSE评价指标,通过计算模拟比较了在不同数据集大小下,LOF-K-means聚类算法、文献[14] K-means聚类算法和传统K-means聚类算法的综合SSE评价指标,得到LOF-K-means聚类算法最优。 3)将LOF-K-means聚类算法用于分析用沙坝矿微震事件分布特征,得出最佳分组数为7。其中C1,C7簇主要受断层滑移的影响;C6簇主要受矿山生产活动的影响,为矿山微震活动性分析提供了一种有效的方法。
2 聚类算法的优化
2.1.1 异常事件检测

2.1.2 初始聚类中心的选择



2.1.3 LOF-K-means聚类算法

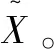
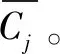

2.1.4 评价指标
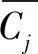
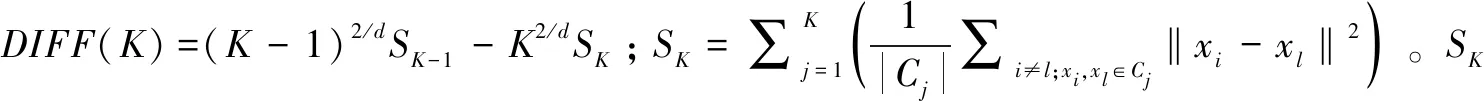
3 模拟测试


4 矿山微震监测应用
4.1 用沙坝矿微震系统

4.2 矿山微震事件的聚类分析




5 结论

