基于元胞自动机恐慌状态下人群疏散模型研究*
陈长坤,童蕴贺
(中南大学 防灾科学与安全技术研究所,湖南 长沙 410075)
0 引言
行人的心理因素和行人运动的随机性是人群运动最重要之处,如何更准确地描述人群的运动,特别是理解心理因素和随机行为对行人运动的影响,具有深刻意义。
在行人动力学研究中,基于元胞自动机的仿真技术是1种重要的研究手段。元胞自动机是定义在1个由具有离散、有限状态的元胞组成的元胞空间上,并按照一定局部规则,在离散的时间维上演化的动力学系统。目前元胞自动机模型被成功运用到行人动力学的仿真研究中,包括正常行人流[1]和紧急疏散[2],并且可以准确描述和重现行人疏散行为,比如从众效应[3],亲情行为[4],小团体行为[5]和竞争与合作[6]等。在这些模型中,基于元胞自动机的场域模型[7],因其简易性和可扩展性,在近年来得到了大量应用。
人群在疏散过程中,尤其是在资源匮乏的情况下,恐慌是其主要的心理和行为形式,恐慌的个体更倾向于表现出非适应行为。很多研究者对行人恐慌行为做了深入的研究,Fruin[8]介绍了恐慌参数的概念,研究发现:恐慌参数较低时,人员密度对疏散速度有很大影响,而恐慌参数高时,更容易发生拥塞的瓶颈;Helbing等[9]建立了数学函数,表明期望速度随着恐慌程度的变化而变化,并验证了在恐慌状态下“快即是慢”的效果;王春雪等[10]根据恐慌心理量表和调查问卷,建立了地铁应急疏散恐慌程度模型,并根据试验数据和相关事故经历对模型进行了修正;王霞等[11]把反映恐慌心理的紧张程度的量化公式引入社会力模型,并考虑了个体的从众行为对个体选择目标方向的影响,发现恐慌心理在一定程度上影响疏散效率。
上述研究对恐慌情绪的内涵和对行人疏散行为的影响做了深刻的分析。此外,恐慌作为一种情绪,不仅对个体产生影响,其本身可以通过疏散个体之间的情绪感染而蔓延。Helbing等[9]模拟群体行为在紧急情况下恐慌逃离的动态特性,结果表明动态特性具有自发性、没有目的、脆弱性等9个特征,根据恐慌情绪是恐慌行为的反映得出结论:恐慌是可以传染的;恐慌情绪感染属于疏散群体内部的情绪同质化体验,该体验被他人所激发,并使接收者的情绪与最初的输出者趋于一致,并且在多人交互中不断增强[12];Wang等[13]建立了基于定性知识的大规模疏散系统仿真模型,研究了一些因素对恐慌蔓延的影响,该模型证实了灾害的严重程度与恐慌蔓延呈指数正相关,救援指导的有效性受到人群中主导情绪的影响,因此,恐慌在人群中的蔓延会对行人行为产生重要影响,是不可忽略的。
本文结合决策理论和情绪感染相关理论,同时考虑了恐慌情绪对行人决策的影响和恐慌情绪本身的动力学特性,如情绪感染和衰减等,采用元胞自动机方法,建立基于场域模型的考虑恐慌的行人决策修正模型,采用该模型研究恐慌情绪对人群疏散行为的影响。
1 模型
1.1 模型概况
本文采用二维元胞自动机方法,行人所处的空间是1个尺寸为35×35的元胞空间,每1个元胞最多被1个行人占据,尺寸为典型个体占地面积0.4 m×0.4 m。元胞的邻域采用半径为1的Moore邻居,包括中心元胞及周围的8个元胞。模型场景设置为1个单出口的矩形房间,出口位于单侧墙壁的中间位置,出口宽度为0.4 m,每个时间步仅允许1个行人通过。初始时刻,行人随机分布在房间内。

图1 元胞(i, j)的邻域及可能运动的方向Fig.1 Neighborhood domain of cell (i, j) and possible directions of motion
在疏散过程中,并不是所有行人都可以理性做出最优移动策略,这与行人本身的心理状态有关。在恐慌状态下,行人更有可能做出非理性决策,并且恐慌程度越大,行人就越有可能丧失主观判断,在惊慌失措的情况下做出不利的反应。恐慌作为一种情绪,有自己的动力学特征,不仅对个体产生影响,其本身也会衰减或者通过疏散个体之间的情绪感染而蔓延,在人群交互作用中不断增强。此外,行人会随着位置的变化而使恐慌减弱,比如当行人疏散到出口附近,恐慌情绪会下降。
在本模型中,同时考虑到了恐慌对行人决策的影响以及恐慌情绪本身的动力学特征,采用静态场域模型计算行人的最优移动策略,采用恐慌情绪决策修正模型体现行人的非理性决策,采用SIS模型和情绪衰减模型模拟恐慌情绪的感染与衰退。模型基本算法如下:
1) 定义初始行人位置和恐慌参数;
2) 根据静态场域模型计算行人的最佳运动策略;
3) 根据情绪感染和衰减模型计算行人的恐慌参数;
4) 当个体的恐慌参数小于临界值,行人做出最佳移动策略;当个体的恐慌参数大于临界值,行人按照修正的决策模型进行移动;
5) 当所有个体都成功完成疏散后,结束进程。
1.2 恐慌状态下行人运动模型
1.2.1 最优决策模型
本文采用静态场域模型模拟行人的最优决策。在每个时间步,行人根据转移概率p选择最佳移动位置。定义pij为元胞(i,j)的转移概率,计算公式如式(1)所示:
pij=Nexp(ksSij)αij(1-nij)
(1)
式中:N为标准化因子,以确保 ∑pij=1;Sij表示静态场域,其系数为ks;αij为类型标识因子,若目标元胞为障碍物,则αij=0,否则αij=1;nij为状态标识因子,若目标元胞当前时刻有行人占据,则nij=1,否则nij=0。
静态场Sij与该元胞位置与出口的距离成反比,距离出口越近的位置对行人有越高的吸引力,计算公式如下所示:
(2)
式中:xe和ye分别表示出口坐标值;xij和yij表示元胞的坐标值。
1.2.2 恐慌情绪量化及算法
恐慌情绪对行人的决策产生影响。本模型采用恐慌参数p(0≤p≤1)对行人的恐慌程度进行量化,行人的初始恐慌参数通过正态分布函数确定,见式(3)。
pt=0~N(μp,σp)
(3)
式中:t为时间步;μp和σp分别为正态分布函数的均值和方差。在疏散的初始阶段,人群恐慌值较低,μp取值为0.1;为避免人群异质性对人群恐慌特性的影响,σp取值为0.01。
本文采用SIS模型模拟恐慌情绪的传播。S为易感者,为恐慌情绪的接收者;I为感染者,为恐慌情绪的传播者,同时也可以接收其他感染者的情绪感染,加重恐慌程度。感染者和易感者可以相互转变,当易感者恐慌情绪积累到某一值,转变为感染者,可以将恐慌情绪传播给他人;当感染者情绪衰减到某一值,可转变为易感者,不再传播恐慌情绪,但可以接收其他感染者的情绪感染。定义恐慌情绪阈值η为易感者和感染者的情绪临界值。某一时刻某一个体的恐慌情绪计算,见式(4)。
(4)

行人的恐慌情绪本身会发生衰减,而且会在快要达到出口时得到大幅度下降。恐慌的衰减值计算如下:
(5)
式中:pdecay为情绪衰减值;α为行人在出口附近的情绪衰减速率;β为行人情绪本身衰减速率;tu为个体最近受到情绪感染时间;d为行人与出口的距离,m;Re为情绪衰减有效半径。
1.2.3 考虑恐慌的决策修正模型
当行人的恐慌情绪未积累到一定程度,行人有能力做出最佳行动策略。当行人的恐慌值积累到一定程度行人就有可能做出非理性行为,且恐慌值越大,行人就越有可能做出不利行动。定义pc为决策修正概率,为行人改变当前运动策略的概率,如式(6)所示,pc与行人的当前恐慌值有关。
pc=λp
(6)
式中:λ为调节因子。当pc<η时,行人会做出最佳移动策略;当pc≥η时,行人会以概率pc做随机运动。
2 模拟及分析
2.1 恐慌行为对疏散效率的影响
为研究恐慌行为对疏散效率的影响,分别进行考虑恐慌和不考虑恐慌情绪2种情况下行人疏散仿真。模拟次数为100次,设定情绪传递值Δp为0.05,出口情绪衰减速率α为0.8,情绪自衰减速率β为0.1,恐慌情绪阈值η为0.1。恐慌情绪对疏散时间的影响见图2。

图2 考虑恐慌和未考虑恐慌情况下疏散时间对比Fig.2 Comparison of evacuation time with considering panic and without considering panic
如图2所示,在考虑恐慌情绪的情况下,每1次模拟所需疏散时间均大于不考虑恐慌情况下的疏散时间。考虑恐慌情绪时的平均总疏散时间约为413 s;不考虑恐慌情绪时的平均总疏散时间约为310 s,差值可达24.65%,说明恐慌情绪对行人疏散行为产生重要影响,在一定程度上降低疏散效率,这与王霞等[11]的研究结果一致。
为研究恐慌情绪对疏散效率的影响机制,对考虑恐慌和不考虑恐慌2种情形下房间内剩余人数随时间变化情况进行了分析,如图3所示。当不考虑恐慌情绪影响时,房间内人数的减少接近于线性变化,说明了在该场景下,出口疏散效率的限制是影响行人疏散的最重要因素;当考虑恐慌情绪影响时,房间内剩余人数的变化会产生一定的波动,尤其是当时间为400 s左右时,其波动更大,这是因为恐慌情绪会对行人决策产生不利影响。当行人占据一定的疏散优势时,比如在出口附近,受到恐慌情绪影响,做出非理性行为,不仅浪费了自身的疏散优势,并且会占据其他行人的最优疏散路径,降低其他行人的疏散效率,从而导致整体疏散效率的下降,疏散时间延长。
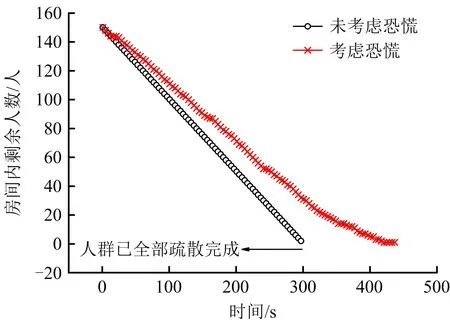
图3 考虑恐慌和未考虑恐慌情况下房间剩余人数随时间的变化Fig.3 Change of number of remaining people in room against time with considering panic and without considering panic
2.2 恐慌情绪阈值的影响
恐慌情绪阈值对疏散时间的影响如图4所示,行人疏散时间随恐慌阈值η的增加而减少,最后稳定在300 s左右。当恐慌情绪阈值η较小时,行人不能按照最优路径运动,导致疏散效率降低,延长了疏散时间。当恐慌情绪阈值0.5时,疏散时间达到最小值,且基本上不会随着恐慌情绪阈值的增加而变化,这是因为情绪阈值较大时,绝大部分行人的恐慌值低于情绪阈值,可以按照最优策略进行疏散,因此当恐慌情绪阈值继续增加时,疏散时间也不会减少。
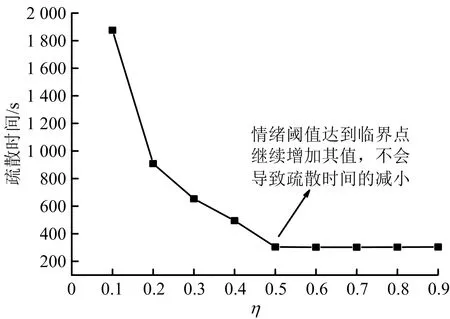
图4 恐慌情绪阈值η对疏散时间的影响Fig.4 Influence of panic emotion threshold η on evacuation time
图5表示了不同恐慌情绪阈值时恐慌人数随时间变化情况。恐慌人数随着疏散时间的增加而减少,并且随着恐慌情绪阈值的降低而增加。当恐慌情绪阈值较小时,在每个时间步,恐慌人数的比例上升,因此导致了人群恐慌行为的增加,延长了疏散时间。

图5 不同恐慌情绪阈值时恐慌人数随疏散时间的变化Fig.5 Change of number of people with panic against evacuation time under different panic emotion thresholds
2.3 情绪衰减速率的影响
恐慌情绪随着行人的运动在人群中传播,但情绪本身也会衰减,包括恐慌情绪自身的衰减和行人到达出口附近的恐慌情绪衰减。图6显示了情绪自衰减速率对恐慌情绪在人群疏散过程中传播的影响。如图6所示,当β值变化时,人均恐慌值呈现出2种不同的变化。当β小于0.01 时,人均恐慌值随着疏散时间的增加总体上是上升的趋势;当β大于0.01 时,人均恐慌值随着疏散时间增加缓慢下降,最后降低至0。这说明了当β值较低时,恐慌情绪的感染速度比其衰减速度高,因此人均恐慌值上升;当β较高时,恐慌情绪的感染速度低于其衰减速度,因此行人逐渐从恐慌状态转变为正常状态。
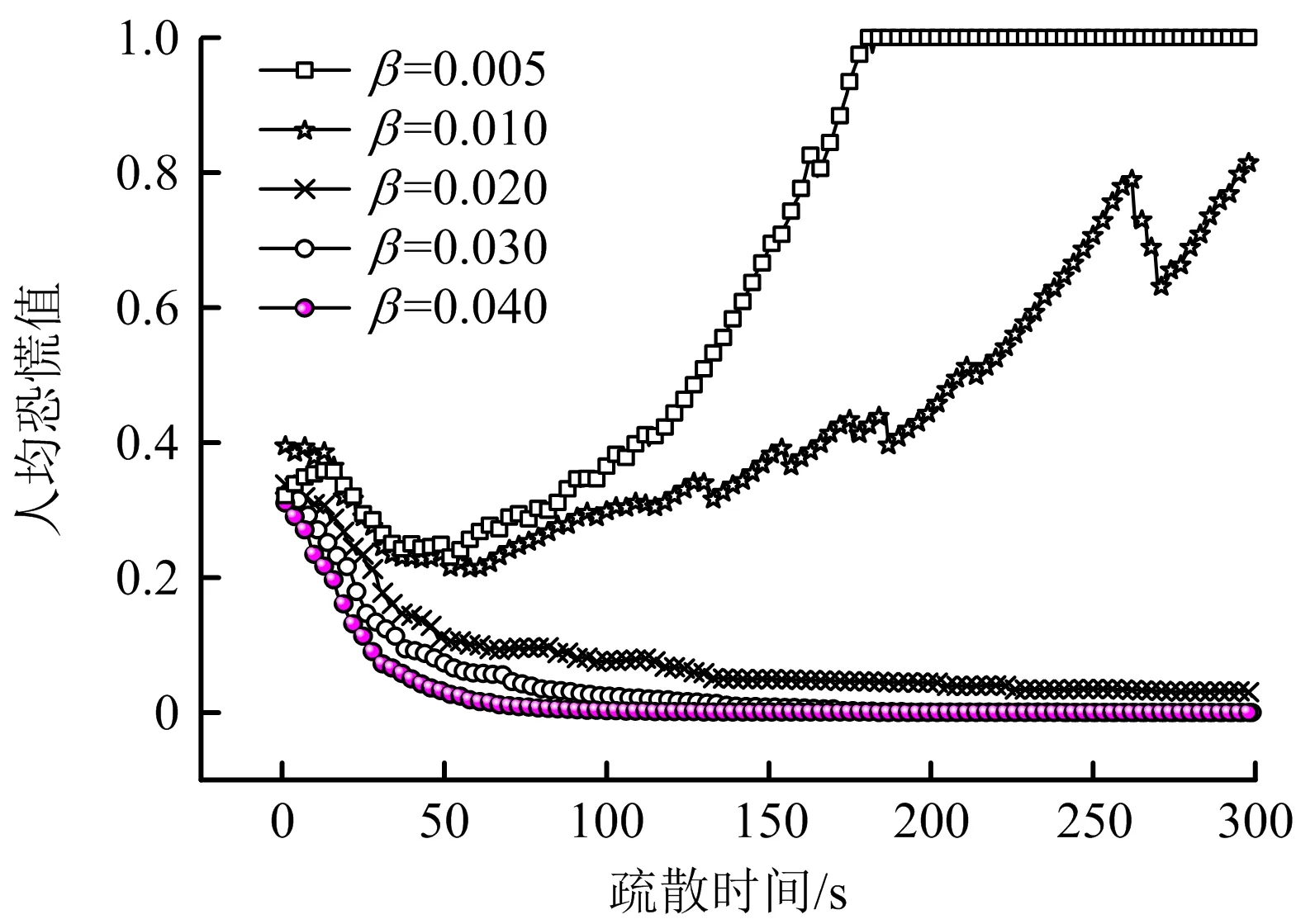
图6 不同情绪自衰减速率时人均恐慌值随时间的变化Fig.6 Change of panic value per person against time under different self-attenuation rates of emotion
图7显示了行人在出口位置情绪衰减速率对情绪传播的影响。当β值为0.01 时,人均恐慌值随疏散时间逐渐上升,且当α值增加时,人均恐慌值较大,增长速度较快。这说明了此时在疏散过程中,人群恐慌情绪的感染速度比衰减速度要高,且出口情绪衰减速率越低,恐慌情绪的感染速度越快;当β值为0.02 时,人均恐慌值随时间逐渐下降,且当α值增加时,人均恐慌值较小,增长速度较低。这说明了此时在疏散过程中,人群恐慌情绪的衰减速度比感染速度要高,且出口情绪衰减速率越高,恐慌情绪的感染速度越慢。此外,对比图7(a)和7(b)可以发现,当β为一定值时,α值的变化只是影响恐慌情绪的蔓延或衰减速率,而当β变化时,恐慌情绪整体蔓延或衰减趋势会发生变化,因此β值是影响人群中恐慌蔓延的关键因素。

图7 不同出口情绪衰减速率时人均恐慌值随时间的变化Fig.7 Change of panic value per person against time under different self-attenuation rates of emotion at exit
2.4 行人密度的影响
行人密度是基于元胞自动机的模型中常用的变量,表示模拟的行人与房间可容纳行人总数量的比值,一定程度上表征了人员密度。图8为疏散时间与行人密度的关系。由图8可知,100次模拟结果高度重合,随着行人密度的增加,所需要的疏散时间也相应增加,这是因为出口有限的疏散能力限制了人群的疏散,适当增加出口数量和宽度有利于人员的逃生。

图8 疏散时间与行人密度的关系(100次模拟)Fig.8 Relationship between evacuation time and pedestrian density (100 times simulation)
图9显示了不同行人密度时恐慌情绪随时间的变化情况。由于行人密度不同时,情绪值总量发生变化,为方便对比分析,采用人均恐慌值作为变量研究行人密度对恐慌情绪传播的影响。由图9可知,当行人密度较大时,人均恐慌值也较大,衰减速度较大;当行人密度较小时,人均恐慌值在任意时刻均低于行人密度较大时的人均恐慌值,且衰减速度较小,在100 s时就衰减到0值附近。这说明了行人密度的增加使人均恐慌值增加,反映了现实中人群规模较大时行人疏散更为恐慌的现象。由于情绪感染有一定的范围,即感染者只能感染一定半径内的易感者,因此,当行人密度较大时,人群间发生感染的次数增加,导致了个体恐慌值增加并在人群间形成多次情绪的反复加强,从而使人均恐慌值增加。

图9 人均恐慌值-时间图Fig.9 Diagram of panic value per person over time
3 结论
1)恐慌情绪在一定程度上降低疏散效率,增加行人所需疏散时间。当处于优势疏散位置的行人,由于恐慌做出非理性决策,即降低了自身的疏散效率,亦因占据其他行人的最优疏散路径而导致整体疏散效率下降。
2)情绪自衰减速率是影响人群中恐慌情绪蔓延的关键因素。随着恐慌情绪阈值增加,同一时刻的恐慌人数减小,疏散时间减少,且存在某一临界值,使疏散时间最短。
3)当行人密度增加时,由于出口有限的疏散效率,行人所需疏散时间加长。行人的恐慌程度随着行人密度的增加而增加,这是因为人群规模较大时,恐慌情绪的感染次数增加,并在人群中得到反复加强,从而使人均恐慌值增加。

