一类加法Allee效应下的捕食-食饵系统的动力分析

岳宗敏, 卢 琨

(陕西科技大学 文理学院, 陕西 西安 712000)

0 引言

一般来说，当种群密度稀疏，或者生存环境的变化，或者种群不聚居导致繁殖大规模减少等等，都较容易受到Allee效应的影响.1931年，美国科学家Allee[1]提出了Allee效应之后，这一现象引起了很多国内外学者的重视[2-6].文献[6]中研究了具有加法Allee效应的Leslie-Gower捕食-食饵模型：

给出了解的全局稳定性以及动力分析.文献[7-10]研究表明带有保护的食饵种群更容易发生Allee效应.本文在文献[6]的基础上考虑食饵带有保护区域[11]的如下系统：

(1)

把食饵的生长区域分成两部分：非保护区域Ω1和保护区域Ω2，两区域一般不能做到完全隔离，它们之间存在扩散效应，假设扩散效应与保护区与非保护区之间的种群密度差成正比，比例系数设为D(>0)，食饵在非保护区与保护区的密度分别为x1(t)和x2(t)，r1与r2对应为各区域内的内禀增长率.食饵在保护区域内不会被捕食，但是会存在Allee效应，所以增长率为

其中m(>0)是Allee效应常数，这里参数r1,r2,a,b,β,k1,k2均为正.

1 模型分析

考虑到食饵的迁移进程比食饵与捕食者之间相互作用的进程快得多，所以可以利用两个不同的时间尺度来表述模型[12,13]，一个是食饵迁移的快系统，一个是种群之间相互作用的慢系统.

(2)

代入系统系统(2)中，可得

(3)

在系统(3)中令ε=0，可得x=C(C为某个常数)，系统(2)或(3)可变为

其解为

(4)

2 慢速系统的动力行为分析

在系统(4)中，记

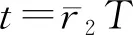
(5)

2.1 解的一致有界性

所以，对于系统(5)的第二个方程，有

定义w(t)=x(t)+y(t),两端对t求导得

由微分不等式原理对于所有t≥T≥0有

0≤w(t)≤M-(M-w(T))e-(t-T),

证毕.

2.2 平衡点的存在性

在系统(5)中，记

令

(6)

易见系统(5)有边界平衡点为

E0(0,0),E1(0,k2).

对于

(7)

若方程(7)有解，则为

(8)

定理2(边界平衡点的存在性)

(a)当0

b<1时，系统(5)有四个边界平衡点：

(c)当m=br且b<1时，系统(5)有三个边界平衡点：

E0(0,0),E1(0,k2),E2(2(1-b),0).

E0(0,0),E1(0,k2),E23(1-b,0).

可得：

x3+Ex2+Fx+H=0

(9)

这里

设

λ=E2F2-4F3-4E3H+18EFH-27H2,

由三次方程根的判别盛金公式可知：

当λ>0时，方程(9)有三个不相等的实根；

当λ=0时，方程(9)有三个实根，其中两个为重根；

当λ<0时，方程有唯一实根.

根据式(6)～(8)可得系统(5)的两条等倾线为

(10)

图1 系统(5)第一象限正平衡点情形

令φ′(x)=0，可得：

(11)

根据方程(7)、式(8)可知

(12)

把式(12)代入式(11)可得：

定理3(弱Allee效应下，即0

(a)下列条件任一成立时，系统(5)有唯一正平衡点：

(b)下列条件成立时，系统(5)有两个正平衡点：

(c)下列任一条件成立时，系统(5)没有正平衡点：

定理4(强Allee效应下，即br≤m成立时正平衡点的存在性)

(a1)λ=0时，系统(5)有唯一正平衡点；

(a2)λ>0时，系统(5)有两个正平衡点；

(a3)λ<0时，系统(5)没有正平衡点.

2.3 平衡点的稳定性

系统(5)的近似线性系统的雅可比矩阵为

(13)

定理5(边界平衡点的稳定性)

(a)强Allee效应下，即br

(c)当0

证明：(a)在E0点的雅可比矩阵为

(14)

由式(14)可知

当br

00，TrJ(E0)>0,

而[TrJ(E0)]2-4detJ(E0)<0,

E0点为不稳定的结点.

(b)在点E1(0,k2)的雅可比矩阵为

(15)

由式(15)可知

[TrJ(E1)]2-4detJ(E1)>0,

E1点为稳定的结点.

(16)

从式(16)可得

(c)当0

detJ(E3)>0,TrJ(E3)>0，

证毕.

若记条件(A)和(B)如下：

(A)弱Allee效应下，

0

(B)强Allee效应下，

定理6(两个正平衡点E-(x-,y-),E+(x+,y+)的稳定)

当λ>0时，记

若条件(A)或者(B)任一成立时，正平衡点E-(x-,y-)都是鞍点；

若条件(A)或者(B)任一成立时，

(a)当μ<μ*，正平衡点E+(x+,y+)都是不稳定的焦点或结点；

(b)当μ>μ*，正平衡点E+(x+,y+)都是稳定的焦点或结点；

(c)当μ=μ*，正平衡点E+(x+,y+)周围出现Hopf分支，E+(x+,y+)外围存在极限环.

证明：系统(5)在点E±(x±,y±)的雅可比矩阵为

所以

若μ<μ*时TrJ(E+)>0,μ>μ*时TrJ(E+)<0，所以(a)、(b)都成立.当μ=μ*时，TrJ(E+)=0,所以对于特征方程

α2-αTrJ(E+)+detJ(E+)=0

由Poincaré-Andronov-Hopf分支理论可知，系统(5)在E+(x+,y+)点周围出现Hopf分支.

证毕.

(a)当且仅当μ>μe，Ee(xe,ye)是渐近稳定的非双曲结点；

(b)当且仅当μ<μe，Ee(xe,ye)是不稳定的非双曲结点；

(c)当且仅当μ=μe，Ee(xe,ye)是一个尖点，周围会出现Bogdanov-Taken分支.

证明：当两个正平衡点重合为一个正平衡点Ee(xe,ye)时，此时雅可比矩阵为

所以

因此(a)、(b)都成立.

证毕.

定理8(弱Allee效应下，唯一正平衡点E(x*,y*)的稳定性(单根))

(b1)若φ′(x*)<0,平衡点E(x*,y*)是渐近稳定的焦点或结点；

证明：系统(5)在点E(x*,y*)的雅可比矩阵为

所以

显然(a)成立时，φ′(x*)<0，所以detJ(E)>0,TrJ(E)<0，从而根据定理3，E(x*,y*)存在且为局部渐近稳定的焦点或结点.下面证明点E(x*,y*)的全局性.

构造Lyapunov函数如下

沿着系统(5)求导得

(17)

注意到φ(x*)=y*，所以考虑在x>0时φ(x)的单调性.从方程(7)和式(10)可知

所以

而当

rk1(1-b)+rb1时，

φ′(x)<0，这也就意味着x>0时φ(x)单调递减，即

(x-x*)(φ(x)-φ(x*))<0，

当(b1)成立时，类似(a)局部稳定性的证明可证；

证毕.

图2 r=2,k1=3,c=1,m=4,k2=2,b=5,μ=0.8时E全局渐近稳定

图3 当r=2,k1=0.3,c=1,m=4,b=5,k2=0.3,μ=0.032 618时点E周围出现Hopf分支

3 具体渐近分析及数值模拟

根据等倾线的分布可以把Ω={(x,y)|x>0,y>0}分成两部分区域：

因为系统(5)在Ω2中没有稳定态，所以任意始于Ω2中的解(x(t),y(t))都会穿过等倾线y=φ(x)垂直向上，从而在等倾线下的轨线y′(t)>0，对应的x′(t)<0.当y>φ(x)时，由系统(5)可知 ，但是随着x(t)减小到一定程度，y′(t)<0.

(a)r=2,k1=0.3,c=1,m=4,k2=0.4,b=5,μ=0.5

(b)r=1.5,k1=0.035,c=0.5,m=2,k2=0.2,b=7,μ=0.1

(c)r=1.5,k1=0.035,c=0.5,m=0.02,k2=0.2,b=8,μ=0.1

(d)r=1.5,k1=0.035,c=0.5,m=2,k2=0.2,b=7,μ=0.080 301图4 系统(5)相平面上的轨线分布图

从上面分析，可以看到慢速系统呈现出了多样的解的变化，接下来把慢速系统的结果应用于系统(2)给出系统(2)在一定条件下的解的变化数值模拟.为了验证结果，所以选取之前对应一组参数:

a=1,m=4,ε=0.05

此时系统(2)的相空间如图5所示.

图5(a)对应于图2中的参数选取，反应出系统(2)有个全局稳定的平衡点，图5(b)对应于图3中的参数选取，反应出系统(2)在平衡点的周围出现Hopf分支，存在一个稳定的极限环.显然这些结果与之前的分析是一致的.

(a)k1=3,k2=2,μ=0.8

(b)k1=0.3,k2=0.2,μ=0.032 618图5 系统(2)的相空间轨线分布图

4 结论

本文研究了带有保护区域的一类捕食-食饵系统，把系统分为快系统和慢系统进行了研究，数值模拟验证了整个系统的动力特征与它的慢速系统是相似的.通过分析慢速系统，可以看到Allee效应下，系统呈现出多样化的动力行为，特别是弱Allee效应下的形态更为丰富.通过分析可以看到，保护区的Allee效应引起系统有了较大的变化，特别是食饵是否能够持续生存，与种群的初始量有关，从图4(c)、(d)可以看到，一部分的轨线稳定到正平衡点E+或者一个极限环，也就是说此时种群会持续生存，但是还有一部分轨线是趋于了点E1,这意味着食饵最终会灭绝.