依标靠纲明确主题，由易到难预设小结——以中考“轴对称图形”复习为例

☉江苏省海门市能仁中学 陆新锋

最近学校备课组打磨中考“轴对称图形”复习内容时，从最初的只涉及轴对称相关综合题的选题方向调整为基于“课标”“考纲”而选题备课，组内同事对这节课的教学目标、主线与选题都有了更深的理解.本文整理该课的教学设计，并跟进教学立意的阐释，供研讨.

一、中考“轴对称图形”复习课教学设计

活动1：观察一组图形

观察以下4个图形（如图1）：

请说说这组图形有怎样的共同点.

预设：学生识别出这组图形都是轴对称图形，引出本课的课题，教师板书本课课题“轴对称图形”.

活动2：研究常见几何图形

例1观察以下3个图形（如图2）：

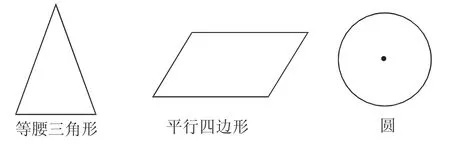
图2

（1）这3个图形中有轴对称图形吗？如果有，你能作出它们的对称轴吗？

预设：提醒学生是“作出对称轴”，需要尺规作图，由学生上台讲解或演示作法即可.

接着给出如下追问：

（2）你还熟悉哪些特殊的等腰三角形？它们的对称轴有几条？

预设：比如，等边三角形有3条对称轴，等腰直角三角形只有1条对称轴，等等，这里不深究，学生答出一种以上即可，主要是为了过渡引出特殊的平行四边形.

（3）平行四边形家族中有没有轴对称图形呢？举例说说.

预设：有.比如，矩形、菱形、正方形.请画一画它们的对称轴.

（4）前面提到了等边三角形、正方形、圆，是否可以猜想：所有正多边形都是轴对称图形？如果是，研究一下它们对称轴的条数.

预设：所有正多边形都是轴对称图形，正多边形都是轴对称图形，它的对称轴条数与边数相等.

练习1：如图3，比较正五边形与正六边形，可以发现它们的相同点与不同点.请你写出它们的两个相同点和两个不同点.

预设：学生可以从多边形的边、角、对角线、内角和、外角和、轴对称性质、对称轴条数等角度分析它们的相同点和不同点.这是一个开放式问题，教学时注意安排不同的学生回答，但不需要太多解答，重要的是让学生知道研究正多边形可以从哪些角度或元素入手.

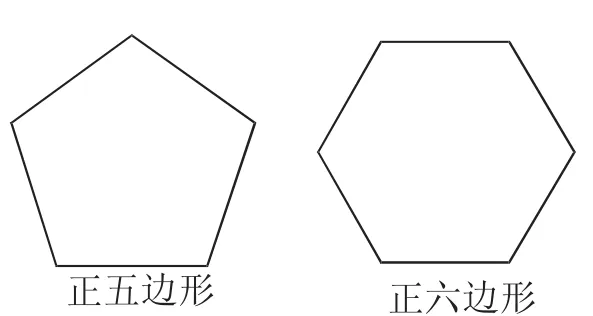
图3

活动3：继续探索几种特殊几何图形的轴对称性质

例2观察一幅三角尺（如图4）：

（1）请将它们分别补成一个正多边形；

（2）等边三角形的3条对称轴交于一点吗？为什么？

（3）如图5，设补成的正方形ABCD的边长为4，点M在边CD上，M、N两点关于对角线AC对称.若DM=1，你能设计一个怎样的问题？

练习2：如图5，正方形ABCD的边长为4，点M在边DC上，M、N两点关于对角线AC对称，若DM=1，则tan∠ADN= .

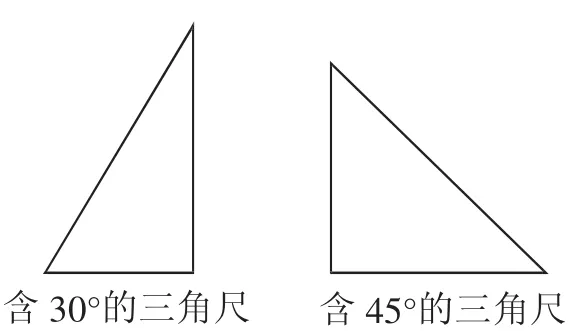
图4

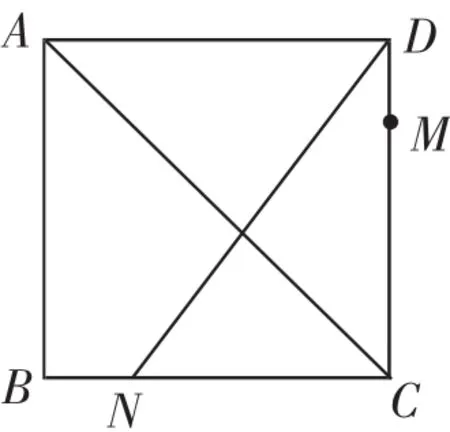
图5

活动4：较难题中常见“轴对称”身影

例3如图6，矩形ABCD中，E是AB的中点，将△BCE沿CE翻折，点B落在点F处.

（1）判断△ABF的形状，并说明理由.

（2）找出图中与△AEF相似的三角形.

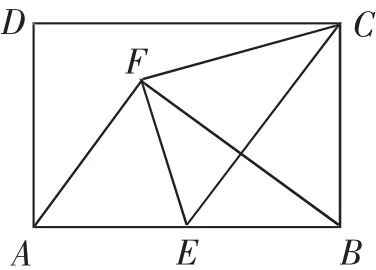
图6

预设：学生独立练习，然后讲评，突出轴对称性质在思路贯通中的作用，再出示一道同类练习（限于篇幅，略去）.

活动5：课堂小结

小结问题1：本课主要复习的是轴对称图形，你一般怎样快速判断一个图形是否为轴对称图形？

小结问题2：在轴对称的两个图形中，对应点的连线段与对称轴有怎样的位置关系？

小结问题3：画出一个三角形关于某条直线对称的三角形时，你会怎样操作？举例说说.

附板书设计：中考一轮复习“轴对称图形”.

二、教学立意的进一步阐释

1.依标靠纲，准确定位复习目标和选题主线

中考复习应对的是各地中考试卷，而中考命题的依据除了课本，主要是国家层面的课程标准（即“课标”）和本地区发布的“考纲”（有些地区称之为“考试说明”），国家层面的“课标”因为内容不多，在我们具体备课时往往能找到的内容表述有限，这时还要结合本地区发布的“考纲”进行研习，分析某个知识点或知识模块在本地区“考纲”中有怎样的表述或对一些具体的知识或技能有哪些明确的能力层级的要求.比如，上文关注的“轴对称图形”课例，整合“课标”与本地区“考纲”后，发现有一些具体的要求，比如，了解轴对称的概念、轴对称图形的概念（只需要达到了解层级），能在自然界或现实图形中识别轴对称图形；理解轴对称的基本性质，成轴对称的两个图形中，对应点的连线被对称轴垂直平分；会探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质（这些技能需要达到理解层级）；能画出简单平面图形（点、线段、直线、三角形等）关于给定对称轴的对称图形（这个技能需要达到掌握的能力层级）.可以发现，这也就是上文课例的复习目标与选题主线.

2.由易到难，从概念梳理复习再到难题讲评

在明确复习目标与选题主线之后，我们需要精心设计和呈现各个不同教学环节，首先要坚持由易到难的选编原则.轴对称图形的复习课例中，我们先通过学生熟悉的一些轴对称图形复习核心概念，并围绕与之相关的一些概念梳理出知识结构，辅以简单的小题及变式练习进行巩固训练，再逐渐过渡到较难习题，并安排学生独立思考后再开展互动式讲评.值得注意的是，发给学生的活动单（或者导学案）要注意留白式呈现，不宜把一些例题的多个设问都印制在活动单上，而是只对一些例题或问题给出一两个简单的设问，将有些渐次生成的后续设问以PPT方式在上课时陆续给出，因为课堂是动态变化的，有时还要结合学情进行增删取舍.我们有时见到老师们手捧一份密不透风的习题单导学案，一题接一题高密度地讲授、灌输，匆忙下课之后，老师把大容量的导学案“讲完”，但是学生接受多少？学生的思维是否最大化参与课堂中的一些问题呢？恐怕要大打折扣吧.

3.注重小结，预设小结问题及时反馈学情

中考复习往往由于习题讲评的任务多，常常出现“拖堂”现象，课堂小结也容易被挤占，这也算是一种“教学遗憾”.我们认为，在备课阶段就要充分预留课堂小结时间，并预设出“独特的”小结问题.比如，上文课例在小结阶段，我们针对本课前面所复习或讲评的典型问题设计的系列问题，既带领学生进行课堂复习小结，同时呼应了本课复习目标与“考纲”要求，当然也是一种反馈学情式的小结问题.

三、写在后面

本文提供的课例并没有涉及图形与坐标的内容，是因为“课标”上另有“图形与坐标”的模块，故没有涉及.这与有些复习资料上“混为一课”不太相同，作为文末，故做说明，以为明辨.