反电动势非正弦的五相PMSM缺一相容错型DTC
闫 震,周扬忠,王凌波
(福州大学, 福州 350108)
0 引 言
与传统三相电机相比,具有高可靠性、高功率密度、高效率、低转矩波动、可容错运行以及可实现低压大功率等优点的多相电机驱动系统越来越受到青睐[1-3]。多相电机提供了额外的自由度,在故障条件下,多相电机中剩余的“健康相”可用于补偿故障并继续驱动控制。
对于反电动势为正弦波的多相电机,可以采用构建虚拟磁链的方法进行容错控制。文献[4-5]以对称绕组六相永磁同步电机(以下简称PMSM)为研究对象,基于虚拟磁链分别提出了缺一相、缺两相的容错型DTC策略。
然而,对于反电动势中含有大量谐波分量呈非正弦波的多相PMSM来说,电机缺相运行时,谐波磁链与基波电流会产生转矩脉动,干扰电机的运行。文献[6]以反电动势为梯形波的五相PMSM为研究对象,在电机缺一相故障情况下,提出了一种通过向定子绕组注入三次谐波电流的方法来消除二次和四次转矩脉动的矢量控制策略。
本文以反电动势非正弦的五相PMSM为研究对象,提出了一种缺一相容错型DTC策略,采用添加转矩给定前馈补偿,消除了因转子三次谐波磁链分量带来的电磁转矩脉动。电机在故障情况下能够稳定运行,具有良好的动态性能。
1 直接转矩控制原理
1.1 五相凸极式PMSM数学模型
本文电机反电动势中除基波分量外,三次谐波分量显著,为了突出主要问题,在以下分析中仅考虑基波和三次谐波分量。图1、图2分别为基波和三次谐波坐标平面。

图1基波坐标系定义

图2三次谐波坐标系定义
图1、图2中:α1β1,α3β3分别为基波、三次谐波静止坐标系;d1q1,d3q3分别为基波、三次谐波转子同步旋转坐标系;θr1,θr3分别为基波和三次谐波平面d轴与α轴之间夹角,且θr3=3θr1;us,is,ψs,ψr分别为电压矢量、电流矢量、定子磁链矢量和转子磁链矢量,这些矢量在基波平面上用下标“1”标示,在三次谐波平面用下标“3”标示,在α轴,β轴,d轴,q轴上投影分别用下标“α”,“β”,“d”,“q”标示,在A轴~E轴上投影分别用下标“A”~“E”标示;δ1,δ3分别为基波和三次谐波平面的定子和转子磁链之间夹角,定义为基波平面与三次谐波平面上转矩角。
根据绕组电压、电流及磁链关系,建立含有三次谐波的五相对称绕组电压及磁链平衡方程,结果如下:

(1)
ψs=Lis+ψr
(2)
式中:Rs为相绕组电阻;L为电感矩阵,L=LsσI5+Ldc1+Ldc3+Lac1+Lac3,Lsσ为相绕组漏电感,I5为5×5的单位矩阵,Ldc1,Ldc3,Lac1,Lac3,ψr表示如下:
Ldcn=Lsmn·

Lacn=Lrsn·
式中:n=1,3,Lsm1=0.5(Ldm1+Lqm1),Lrs1=0.5(Ldm1-Lqm1),Lsm3=0.5(Ldm3+Lqm3),Lrs3=0.5(Ldm3-Lqm3),Ldm1和Lqm1分别为相绕组基波主磁路的直、交轴电感,Ldm3和Lqm3分别为相绕组三次谐波主磁路的直、交轴电感;α=2π/5。ψr=ψf1c1+ψf3c3,ψf1,ψf3分别为永磁体耦合到相绕组的基波、三次谐波磁链幅值;cn=[cos(nθr1) cos[n(θr1-2π/5)] cos[n(θr1-4π/5)]cos[n(θr1-6π/5)] cos[n(θr1-8π/5)]],n=1,3。
为了进一步揭示基波与三次谐波之间的耦合情况,采用式(3)的正交变换矩阵T5,实现五相静止坐标ABCDE向α1β1α3β3z变换,变换过程遵循功率不变原则。

(3)
在α1β1和α3β3静止坐标系中磁链、电压方程及转矩Te推导结果如下:

(4)


(5)
Te=p(isβ1ψsα1-isα1ψsβ1)+3p(isβ3ψsα3-isα3ψsβ3)
(6)
式中:p为电机磁极对数。
1.2 缺一相直接转矩控制原理
1.2.1 控制原理
进一步推导出电磁转矩满足如下关系:
(7)
由式(7)可见,通过控制转矩角δ1,可进一步控制Te1。
对于对称绕组五相凸极式PMSM来说,缺一相故障共有5种可能。但电机绕组是对称的,五相电机缺任意一相故障都可以通过重新标注的方法转化为缺A相故障,因此本文仅介绍缺A相时的缺一相容错直接转矩控制(以下简称DTC)策略。
当五相电机A相绕组断路或A相逆变桥故障后,尽管A相中没有电流流过,但由于互感和永磁体反电动势的存在,A相逆变桥输出电压不恒为0,其值不可忽略。假设A相逆变桥始终输出五相电机A相电压uoA。则五相逆变桥的输出电压可表示:
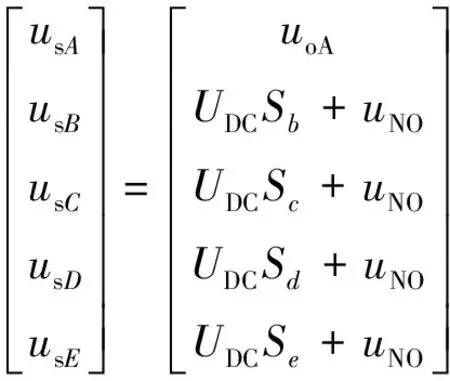
(8)
通过式(3)的变换矩阵T5,可以将式(6)输出电压变换到α1β1平面、α3β3平面及z轴,得:
(9)
1.2.2 三次谐波平面和零序轴系控制
通过式(3)中的T5矩阵的逆矩阵,可以把α1β1α3β3z坐标系的电流变换到ABCDE坐标系中,则此时:

(10)
式(10)可化简:
isα3=-isα1
(11)
进一步可推导出其他四相“健康相”电流表达式如下:

(12)
当采用星型连接的五相PMSM的任意一相开路时,还有三个自由度可用于电机控制,其中两个自由度用来控制五相PMSM基波平面的|ψs1|和Te1,因此还有一个冗余自由度。根据式(11)可知,isα3已被约束,因此,为了降低铜耗,控制isβ3=0。式(9)第四行为β3轴电压usβ3与逆变器开关组合关系,可选择合适的开关组合,将电流误差Δisβ3控制为零。
零序等效电路模型如图3所示。

图3零序等效电路
得到零序电压与零序电流关系如下:
(13)
式中:usz为零序电压;isz为零序电流。
由于五相电机中性点不引出时,isz恒为0,则由式(9)和式(13)可得:


(14)
1.2.3 逆变器开关组合确定
假设isα3=-isα1=-Iα1sinθr1,Iα1为基波平面静止坐标系α1轴电流isα1幅值,则根据式(5)可得:
ωr[Lsσ+2.5Lsm3+2.5Lrs3cos(6θr1)]·

6.25ωrLrs3Iα1cos(7θr1)+
8.75ωrLrs3Iα1cos(5θr1)-

ωr(Lsσ+2.5Lsm3)Iα1cosθr1
(15)
通过式(15)参数代入计算可得,usα3幅值较小,可以忽略不计。再结合式(14)可将式(9)可化简如下:
(16)
当A相开路后,逆变桥的4个桥臂共有16(24=16)个开关组合。Sa~Se为5个逆变桥臂开关管通断状态,上管导通值等于1,下管导通值等于0。
根据式(16)前两行可以画出基波平面定子电压usα1+jusβ1矢量图,如图4所示,矢量编号即为SbScSdSe四位二进制数。根据式(16)第四行可以画出β3轴电压usβ3如图5所示,其中,usβ3为正的基本电压矢量编号有1、4、5、7、12、13;usβ3为负的基本电压矢量编号有2、3、8、10、11、14,usβ3为零的电压矢量编号有6和9。

图4A相开路时α1β1平面内定子电压矢量usα1+jusβ1

图5A相开路时β3轴定子电压矢量usβ3
为了达到更好的控制效果,需要将部分电压矢量进行合成,具体按以下方式合成矢量:40(1,13),41(8,11),42(2,14),43(4,7)。根据平行四边形原则,两个基本电压矢量各工作半个控制周期,来等效成一个电压矢量。
为了实现基波平面转矩和磁链的稳定控制,同时将Δisβ3控制为零,本文采用的最优逆变桥电压矢量控制。以缺A相为例,表1、表2为最优开关矢量表。表1、表2中:τ=1和-1分别代表电机转矩增大和减小;Ф=1和0分别代表电机基波平面磁链幅值增大和减小。

表1 缺A相最优开关矢量表(Δisβ3>0)

表2 缺A相最优开关矢量表(Δisβ3<0)
控制步骤如下:
(1)在图4的基波电压平面中,采用后续方法按逆时针方向依次分为20个不等的电压矢量扇区,用θsi表示,其中i1,2,…,20。每个扇区均处于图4中相邻两个电压矢量所夹区域中,且同时要保证当定子基波磁链矢量ψs1。
处于该扇区内旋转时,与其垂直线必须始终处于某一相邻的两个电压矢量所夹区域中。
(2)根据isβ3的变化趋势,在图5中选择合适的开关组合,将电流误差Δisβ3控制为零。
(3)判断基波定子磁链矢量ψs1所处扇区,并根据此,分析步骤(2)中选择出的各个开关组合作用引起基波定子磁链幅值及其电磁转矩控制效果,即增大或减小。
(4)结合步骤(2)和步骤(3)综合选择,列表获得最优开关矢量表,根据该表获得最优开关组合实现基波平面定子磁链幅值及电磁转矩跟踪其给定值,同时将电流误差Δisβ3控制为零。
(5)采用上述步骤在某个扇区内无法找到满足控制需要的基本电压矢量,则再选择满足控制需要的合成矢量。
1.2.4 转矩给定前馈补偿
由于电机转子永磁体磁链中含有大量的三次谐波分量,电机在缺相情况下,由于不解耦,会与基波平面电流相互作用产生转矩脉动二次和四次谐波。此外,由于isα3=-isα1,在电机加载运行时,isα3不为零,也会与永磁磁链产生转矩脉动。因此,为克服这些转矩脉动对电机运行的影响,基波平面转矩给定值要加上一个负的三次谐波平面转矩作为前馈补偿,来抵消上述转矩脉动,使电机输出平稳的电磁转矩。转矩给定值前馈补偿示意图如图6所示。

图6转矩给定值前馈补偿示意图
1.2.5 结构框图
图7为本文基于转矩给定前馈补偿的五相PMSM一相开路容错型DTC结构框图。
图7系统控制框图
图7中,isβ3的给定值为零;定子基波磁链幅值的给定值|ψs1|为恒值;虚线框中为转矩给定前馈补偿模块。
2 实验研究
2.1 实验参数
为了验证本文控制算法的正确性,搭建了五相PMSM-DTC系统实验平台,五相PMSM参数如表3所示。

表3 五相PMSM参数
负载采用型号为FZ25-D的电磁粉末制动器,用增量式编码器来检测电机转子位置角。转矩和磁链滞环宽度均为0,PWM控制周期为46μs,逆变器直流母线电压UDC=200V。硬件平台如图8所示。

图8实验平台
2.2 稳态实验分析
为验证本文的缺一相容错型DTC策略的稳态性能,对系统做额定转速下的稳态负载实验。波形如图9所示。

(a) 转速、电磁转矩

(b) B,C,D,E相电流

(c) 定子电流

(d) α1,β1定子磁链
图91 000r/min缺一相时稳态实验波形
从稳态实验波形可见:电机输出转矩下降到4.5N·m,电磁转矩和转速能够稳定地跟踪给定值;由于在基波平面控制总电磁转矩,且将基波磁链幅值控制为恒定值,为克服缺相后永磁体三次谐波磁链对转矩的影响,四相剩余“健康相”B,C,D,E相电流发生畸变,且各相电流幅值不相等;基波平面定子电流非正弦,三次谐波平面电流isα3=-isα1,同时isβ3被控制为零。
2.3 动态实验分析
为进一步验证本文策略的正确性,做负载阶跃实验,缺一相情况下的动态波形如图10所示。从实验波形可得:在负载阶跃瞬间,电磁转矩和转速有微小波动,并能迅速地恢复到给定值,动态反应迅速;剩余 “健康相”相电流均能随负载变化而迅速变化至相应值。

(a) 转速、电磁转矩

(b) B,C,D,E相电流
图101 000r/min缺一相时负载阶跃实验
2.4 无故障切换到故障运行实验研究
为了研究系统在发生故障瞬间的暂态性能,分别做由三次谐波电流注入五相PMSM无故障带载运行切换至一相开路故障运行的实验,实验结果如图11所示。
从图11实验结果可见,绕组故障出现前后,电机电磁转矩和转速变化不大,表明本文控制策略允许电机绕组故障前后的不间断切换;对比故障前后的电流波形可见,故障以后的电机A相电流等于零,为克服缺相后三次谐波磁链对转矩的影响,其余四相“健康相”B,C,D,E相电流波形发生畸变,且幅值不相等;故障前,基波和三次谐波平面电流isα1,isβ1,isα3,isβ3均为正弦波;故障后isα3=- isα1且isβ3=0。

(a) 电磁转矩

(b) A,B,C相电流

(c) D,E相电流

(d) α1β1α3β3定子电流
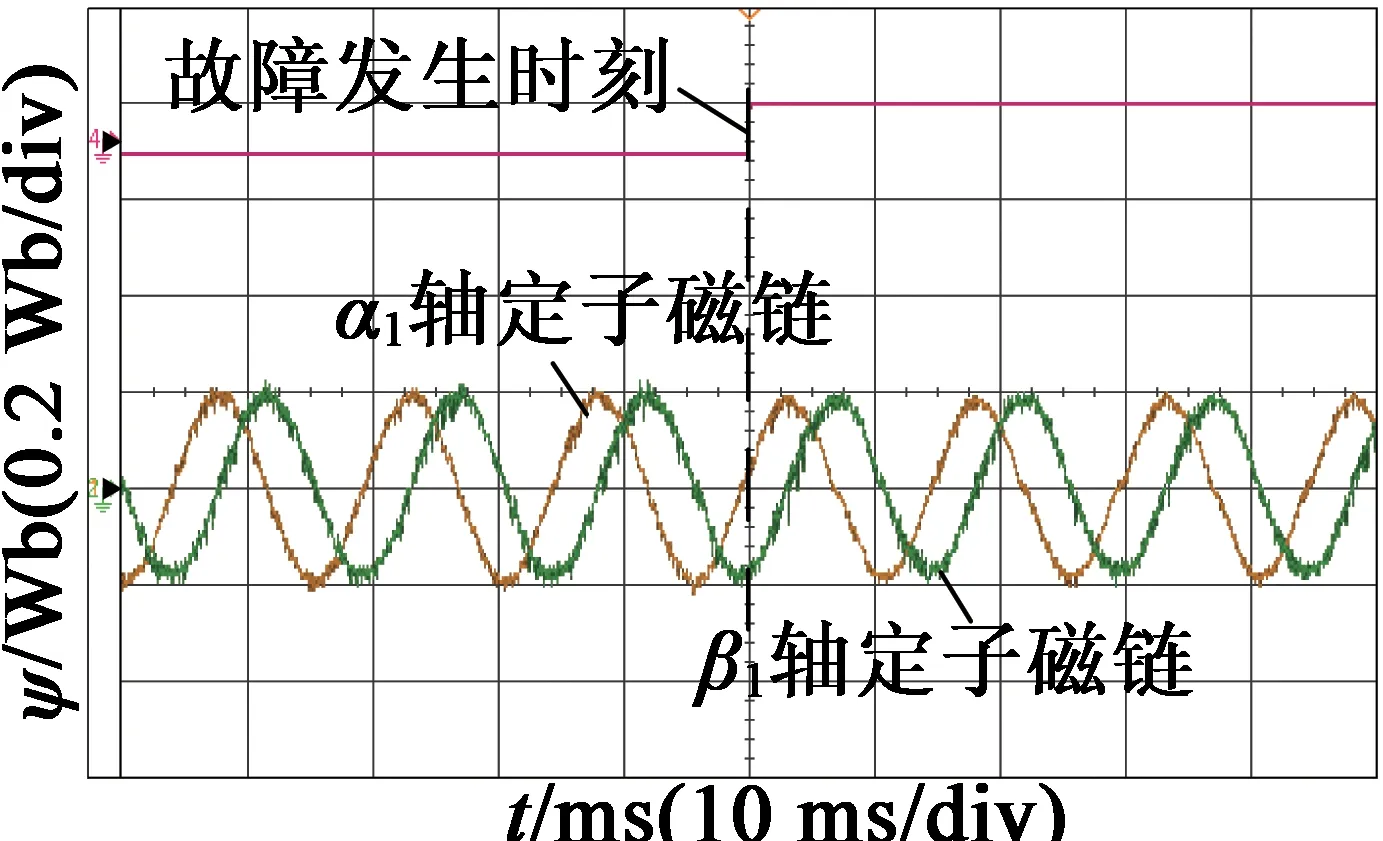
(e) 定子磁链
图111 000r/min时无故障切换到缺一相故障实验
3 结 语
本文针对五相PMSM在任意一相开路情况,研究了新的基于转矩给定前馈补偿的容错型DTC策略,理论分析和实验研究表明:
1) 通过添加转矩给定前馈补偿,电机输出转矩脉动小,电机运行平稳;
2) 在开路故障的情况下,五相PMSM的电磁转矩能够跟踪给定转矩,实现了电机的平稳控制,动态响应迅速;电流isβ3被控制为零;
3) 实现了电机由无故障运行到一相开路故障运行的不间断过渡,转矩过渡平稳,系统切换迅速。

