湿式摩擦副滑摩过程温度场分析及实验验证*

(1.北京信息科技大学机电工程学院,现代测控技术教育部重点实验室 北京 100192；2.贵州交通职业技术学院机械电子工程系 贵州贵阳 550008)

以湿式摩擦副为核心部件的湿式多片换挡离合器是现代自动变速系统与综合传动装置的核心部件之一，广泛应用于履带装甲车辆、大型船舶、起重机、装载机等和工程机械等重型装备。离合器接合过程中，湿式摩擦副处于滑动摩擦状态，产生大量摩擦热，润滑油流经接合界面带走部分热量。但是，由于接触压力的不均匀分布仍会导致摩擦界面温度非均匀分布，产生热弹不稳定性[1-4]，进而导致离合器摩擦副出现热斑、翘曲变形等早期失效形式。随着时间的推移，过高的温度会使摩擦副出现严重磨损、材料脱落甚至烧结为一体[5]，严重影响湿式离合器工作性能。

针对上述离合器摩擦副热失效现象，国内外学者开展了广泛的研究。JEN和NEMENCEK[6]通过分析离合器接合过程，建立热传导物理模型，对单个摩擦副的整体温升情况进行计算，并利用全隐式有限差分的方法对摩擦片的温度场分布进行了数值计算分析。胡宏伟[7]利用建立的摩擦副有限元模型研究了控制压力、相对转速、钢片与摩擦片厚度尺寸对温度场分布规律的影响，根据仿真结果定性地提出了延缓热失效的措施。张加元等[8]利用ANSYS通过间接条件和间接耦合方式，对建立的简化三维模型进行了温度场和应力场仿真计算。张金乐等[9]利用ABAQUS有限元软件，改进了摩擦副径向热流密度输入模型，模拟了温度场与应力场瞬态变化特性。赵家昕等[10]利用热弹不稳定性理论对湿式离合器接合过程中的局部高温区及影响因素进行了理论建模与分析，探讨了摩擦材料的导热性与对偶片厚度对稳定性的影响。ZHAO等[11]提出了多片离合器热弹性变形的二维模型，并通过ABAQUS有限元分析软件研究了在滑摩过程中采用碳-碳摩擦材料的离合器摩擦片的温度场和应力场，分析了离合器摩擦元件产生的热机耦合在不同摩擦片厚度和不同材料下的影响。然而在上述分析中，常忽略摩擦片表面沟槽结构形式，未考虑摩擦副温度场应变场与流场的交互耦合作用；对湿式摩擦副内部多物理场耦合作用及传热过程的分析有待进一步的完善。

本文作者针对摩擦副温度场分布特性和各种影响因素，建立了带有沟槽的摩擦副有限元模型，应用ABAQUS对摩擦副滑摩过程进行了数值模拟，对温度场与应力场分布进行研究，并通过有限元数值模拟和试验研究相结合的方法，分析工作压力、相对转速和润滑流量对界面温度场变化过程的影响。

1 数学模型建立

1.1 热传导模型建立

湿式摩擦副由表面带有沟槽的环状摩擦片与对偶钢片组成，其几何模型如图1所示。

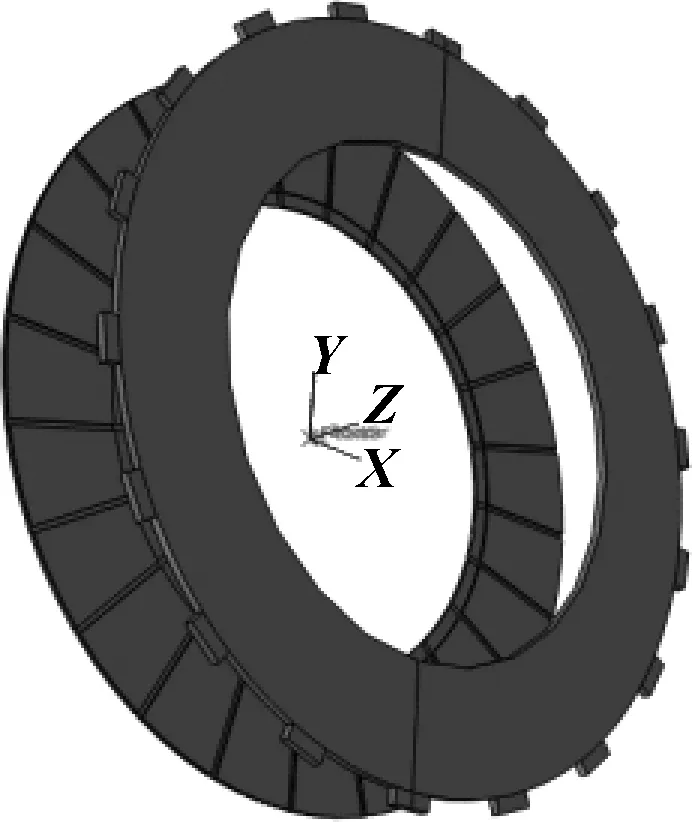
图1 摩擦副示意图

摩擦副结合时，对偶钢片与摩擦片在外压力作用下逐渐压紧，同时由于两者的相对滑动生成摩擦热。若忽略磨损颗粒带走的热量，在直角坐标系下，热流密度为

q(x,y,z,t)=μ(Δω)pi(x,y,z,t)·Δω·r

(1)

式中：q为单位面积某点热流密度；μ为摩擦因数；pi为该点的接触比压；Δω为摩擦片与对偶钢片的转速差；r为该点距摩擦副中心的半径。

摩擦副滑摩过程中整个接触面输入的总热流为

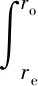
(2)

式中：re、ro分别为摩擦接触面的内径和外径；dA=2πrdr。

某一时刻产生的总热量：

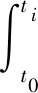
(3)

式中：t0、ti分别为摩擦副滑摩开始时刻和结束时刻。

湿式摩擦副摩擦片与对偶钢片滑摩过程持续时间短，接触界面间隙较小，润滑油主要起到对流换热作用，可认为摩擦产生的热量Q全部被摩擦片和钢片吸收。热量在两者之间分配分别为对偶钢片吸收热量Qs，摩擦片吸收热量Qf，且在温度连续的情况下分配系数与他们的物理属性有关，则分配系数Kq[12]为

(4)

式中：对偶钢片和摩擦片输入的热流分别为qs与qf；λs、λf为导热系数；ρs、ρf为密度；cs、cf为比热容；s、f分别表示为对偶钢片和摩擦片。

湿式摩擦副热传导是一个非稳态传导过程，根据传热学理论，在直角坐标系下建立摩擦副的热传导方程[13]：

(5)

式中：λi为导热系数；ρi为密度；ci为比热容；Ti为摩擦元件的温度；t为滑摩时间；x、y、z为摩擦副某点坐标；i的数值为1、2，分别对应对偶钢片、摩擦片。

1.2 热机耦合模型建立

湿式摩擦副滑摩过程中应力场和温度场相互作用，摩擦副始终处于热机耦合状态。摩擦热与对偶钢片和摩擦面之间的接触状态相互影响，温度分布不均导致摩擦副变形不均，进而影响接触状态，接触状态的变化反过来又影响摩擦热流的输入强度。将式(5)通过Galerkin方法转化为有限元格式：

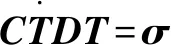
(6)

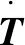
根据热力学理论，在已知温度场求解各部分热应力，温度引起的线应变为

Δε=αΔT=α(T-T0)

(7)

式中：Δε为线应变；α为线膨胀系数；T0为初始温度。

考虑到温度带来的影响，则应力表示为

σ=K(ε-Δδ)

(8)

式中：σ为应力矩阵；ε为应变矩阵；Δδ为温度对应的应变矩阵；K表示为弹性矩阵。

1.3 几何模型与材料特性

依据摩擦副传热过程中两侧盘面状态对称，数值模型取各片厚度的1/2[14]，几何尺寸见表1。摩擦片油槽宽度0.002 mm，深度0.001 mm，竖直型油槽数量为24，油槽横截面简化为矩形，如图2所示。

表1摩擦副几何尺寸

Table1Geometrysizeoffrictionpairs

m

图2 摩擦片油槽有限元模型

有限元模型中，假设摩擦材料各项同性，摩擦过程中温升明显，对偶钢片导热系数随温度变化如表2所示。实验测得摩擦因数约为0.13，摩擦副材料属性如表3所示。

表2 不同温度下对偶钢片导热系数

表3 摩擦副材料属性参数(20 ℃)

1.4 边界条件

1.4.1 运动与压力加载条件

摩擦副滑摩过程中，设置对偶钢片只能沿Z轴移动和转动，约束X与Y方向移动和转动4个自由度，摩擦片只绕Z轴转动，固定其在X、Y、Z方向平移和X、Y方向转动自由度，对偶钢片背面施加均匀压力1.4 MPa。采用直接热机耦合模拟方式，设置摩擦片初始转速为700 r/min，约为72.8 rad/s，接合时间为0.5 s。

1.4.2 热交换条件

湿式摩擦副两接触面间有润滑油流过，不考虑润滑油的热传导及热吸收，认为每个时间点瞬时只有对流换热作用。油槽内表面与液体接触存在对流换热，摩擦副内外圈表面与空气接触，固体与空气对流换热系数取经验值5～25 W/(m2·℃)。在摩擦副具有相对转速时r处的对流换热系数表达式[15]为

(9)

式中：Pr为普朗特系数;Rer为雷诺数;Nu为传质努塞尔数;m1用于定义圆盘表面温度沿径向分布的指数，假设其为线性分布，则m1=1。

摩擦副内外环面对流换热可认为冷却油横掠圆柱体的对流换热：

(10)

式中:v(i,o)为内外环面线速度；d(i,o)为内外环面直径；m2、n为经验系数，分别取0.193、0.618[16]。

摩擦片油槽内有冷却油流过，3个矩形面对流换热系数[17]为

(11)

式中：l为沟槽冷却油特征长度，表达式为l=ro-re。

表4为所用冷却油物理参数。

表4 高级抗磨液压油L-AN32参数(40 ℃)

将上述参数代入式(9)(10)(11)，得出对流换热系数与相对转速的变化曲线，如图3所示。

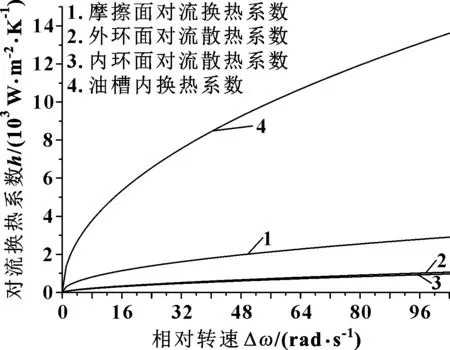
图3 随相对转速变化的对流换热曲线

2 有限元模拟结果及分析

采用ABAQUS软件模拟分析了湿式摩擦副滑摩过程中温度场与应力场的分布规律。图4、图5分别为0.5 s时对偶钢片与摩擦片接触面上的温度场与应力场的分布云图。

图4显示，对偶钢片温度场与应力场分布相似，盘面中间位置平均温度较高，两侧边缘处温度较低；对偶钢片盘面中间圆出现斑点状应力集中区且沿周向不均匀分布；应力集中区所在径向位置与高温区分布类似，两者存在较强耦合关系；温度与机械应力共同影响钢片应力，摩擦副接合过程中，温度场改变了界面的应力分布，根据钢片的材料特性，高温区的线性膨胀较大，接触比压增大，进一步促使应力增大，因此温度高的区域，其机械作用与温度作用的应力均较大。

图5显示，摩擦片温度场分布与钢片类似，但应力场仅在个别位置出现应力集中。这是由于摩擦片材料弹性模量相对较小，可变形度大；由于沟槽的存在，各部分区域热膨胀牵制作用较小，应力分布相对均匀。

图4 对偶钢片温度场与应力场云图

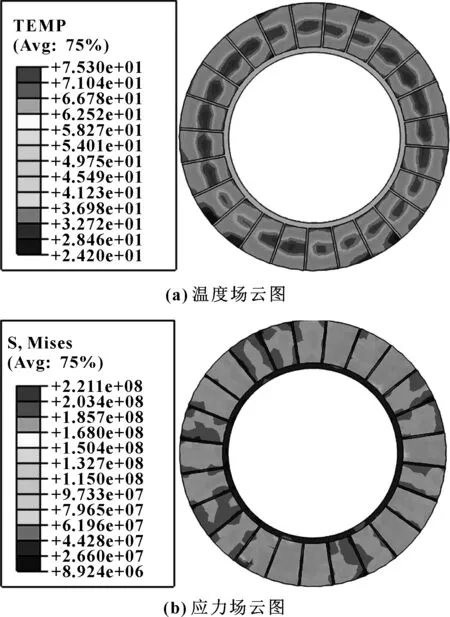
图5 摩擦片温度场与应力场云图

2.1 温度场分析

分别取有限元模型中对偶钢片5个节点(标号：926、924、922、920、918)，摩擦片接触面5个节点(标号：4620、4622、4623、4624、1918)，以研究摩擦副温度场随时间变化规律，节点位置如图6所示。

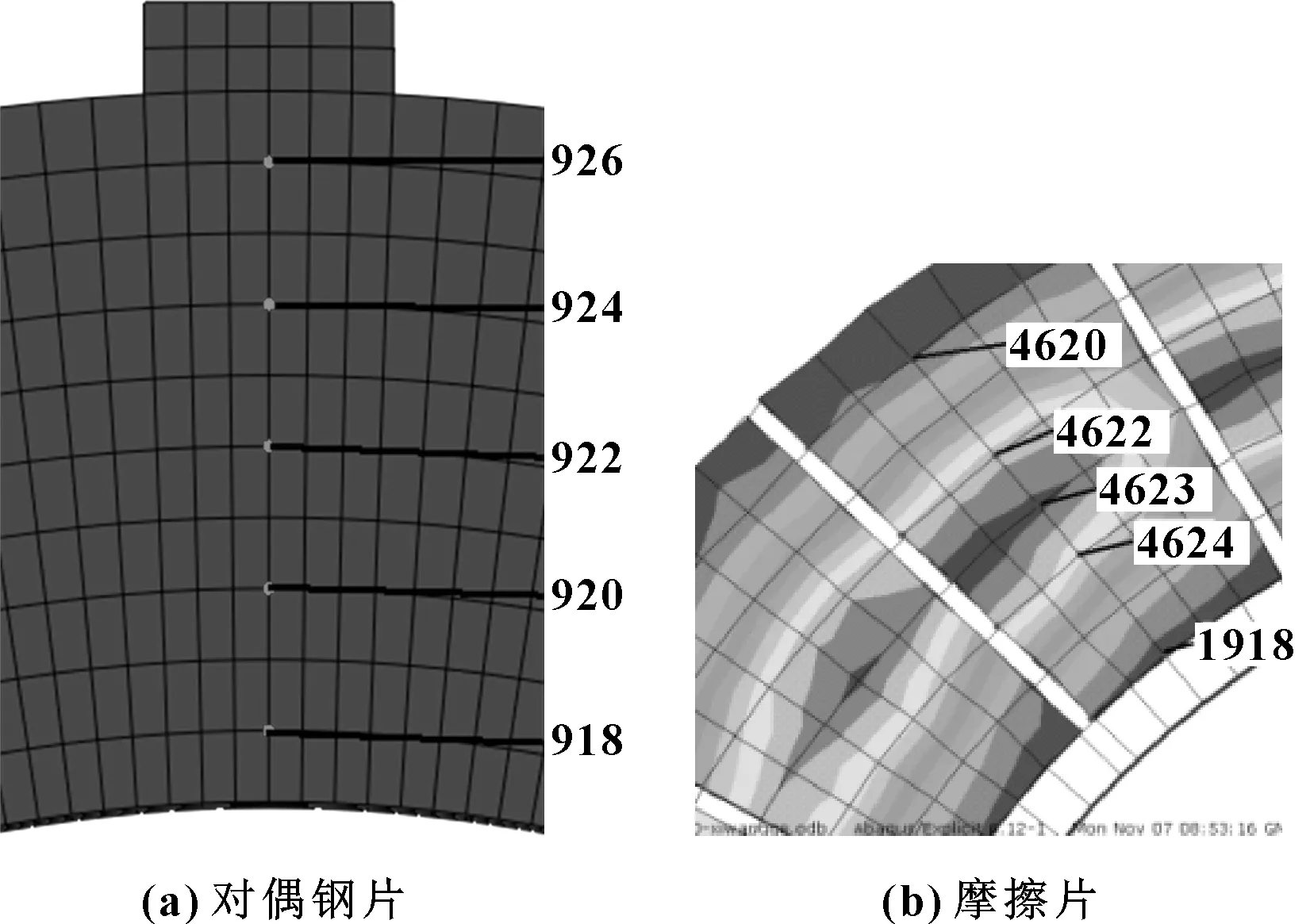
图6 对偶钢片(a)及摩擦片(b)节点示意图

图7所示为对偶钢片各节点温度随滑摩时间变化曲线，其中高温出现在922节点即平均半径位置，且随着时间的增加高温数值持续上升，在t=0.4 s时达到峰值，后开始下降直到滑摩结束。该变化过程说明，摩擦热在滑摩初期不断积累，径向中部位置相对于环面内外边缘处不易散热，累积热量最多，致使出现高温环带，且随时间的推移温度持续上升；滑摩后期，随着相对转速的下降，摩擦热生成量随时间的推移下降显著，热量累积量小于散热量，温度逐渐降低。

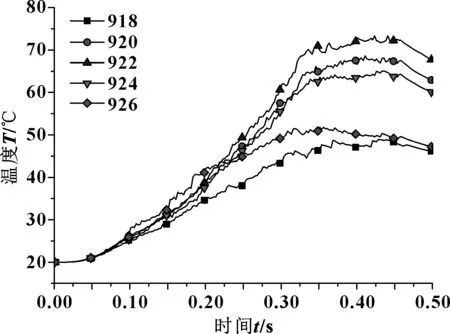
图7 钢片节点温度随时间变化曲线

图8所示为不同时刻对偶钢片盘面温度沿半径分布曲线。图中显示，滑摩初期高温区出现在靠近环面外边缘处，随着时间的推移，高温带逐渐内移，在半径r=105 mm处温度值最大，此时盘面径向温度梯度达到最大约为52 ℃。这是由于，润滑油液从摩擦副所在圆环面中心喷出，流经盘面从外边缘处流出；内环边缘最先被冷却，外边缘处由于与外界空气存在对流换热，初期摩擦热累积量不大时降温较为明显，因而靠近外边缘处由于摩擦热累积，润滑油冷却作用不显著，无外界空气对流，因而成为滑摩初期温度最高处。随着滑摩过程摩擦热生成量增加，大量摩擦热在中径处累积，0.4 s时出现了最高温；随着摩擦热生成量减少，润滑油持续向外边缘处流动，0.4～0.5 s钢片表面整体温度下降。

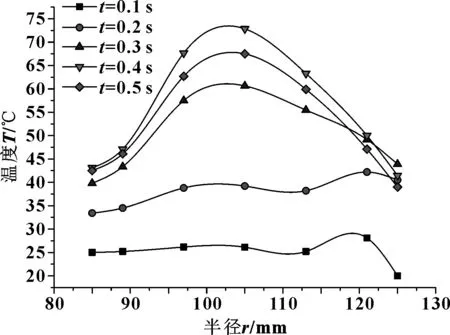
图8 不同时刻钢片温度沿半径分布曲线

由图9可知：摩擦片表面温度分布曲线与钢片类似，中间位置节点4623处温度在滑摩0.4 s时到达最高为82.51 ℃；边缘两侧位置较低，外边缘节点4620与中内圆节点4624处温度，分别低于内边缘节点1918与中外圆节点4622处温度；冷却油流入油槽的速度低于流出速度，摩擦片外边缘对流换热量大于内边缘。摩擦片沿径向温度分布如图10所示，在接合初期，高温带较宽，随着时间的推移高温带逐渐变窄，集中于半径r=105 mm处，摩擦片最大径向温差约为60 ℃。

图9 摩擦片节点温度随时间变化曲线

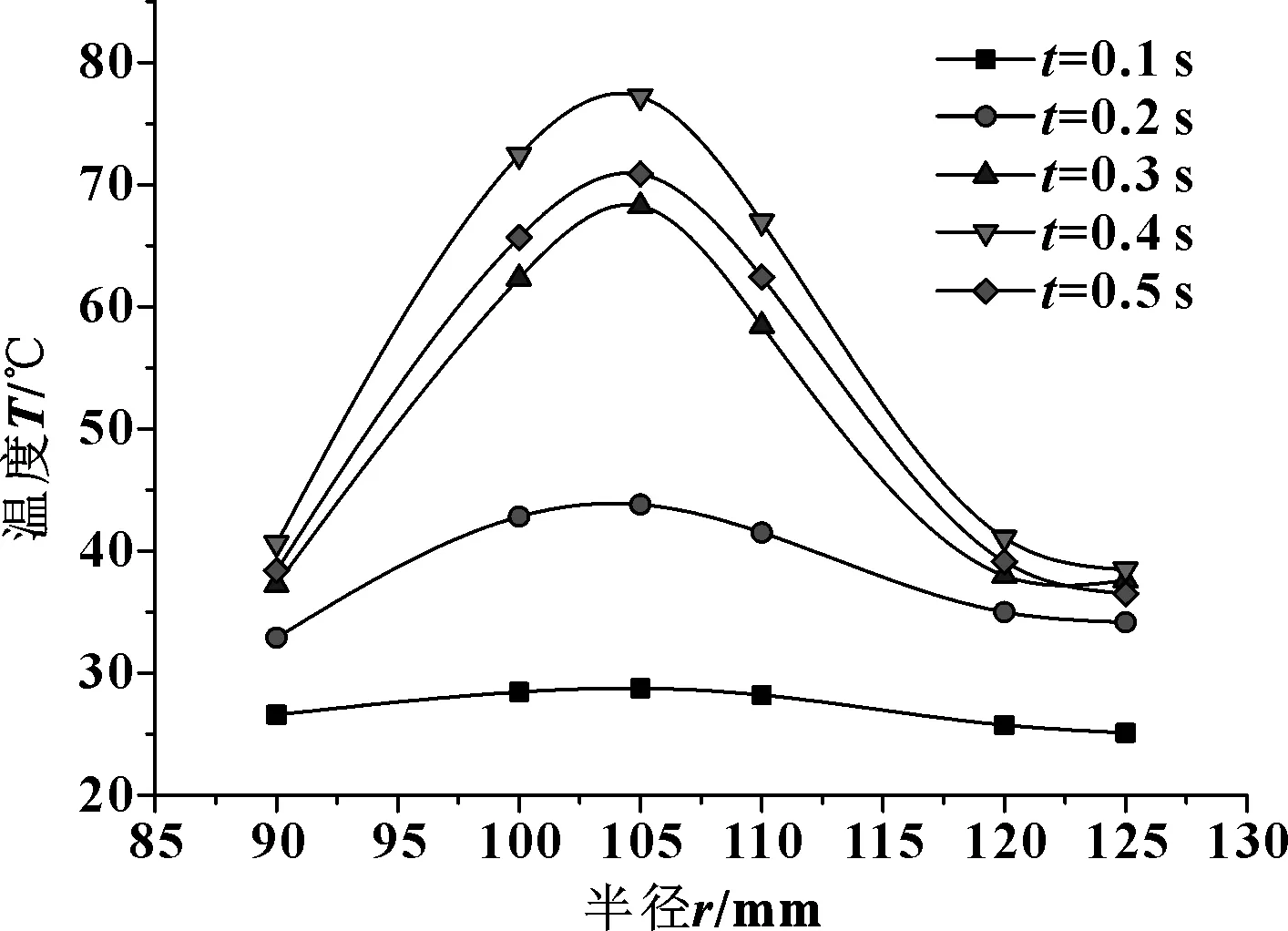
图10 不同时刻摩擦片温度沿半径分布曲线

2.2 应力场分析

图11所示为对偶钢片接触面应力随滑摩时间变化曲线。如图所示应力随时间呈先增大后减小的变化规律，盘面中间位置应力最大，内边缘与外边缘较小；接合时间t=0.4 s时应力最大为1.3×108MPa。结合温度场变化可知，滑摩初期热应力较小，对偶钢片主要由机械应力作用，此时钢片接触面温度较低，热应力影响小，随着时间推移，接触面温度逐渐升高，热应力逐渐起主导作用。

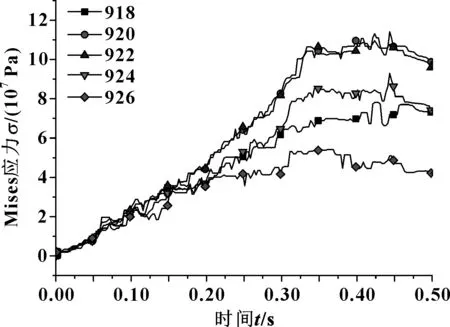
图11 对偶钢片节点综合应力曲线

图12所示为不同时刻钢片节点应力沿径向分布曲线。如图所示，应力集中区主要分布于半径105 mm处，盘面最大径向应力差出现在0.4 s。有限元模拟为热机直接耦合，接触面各节点的温度状态非线性分布致使各节点应力状态发生非稳态变化，两者相互作用过程符合热弹不稳定性特征。

图13所示为摩擦片模型接触面节点综合应力随时间变化曲线，图14所示为摩擦片模型接触面节点综合应力沿径向分布曲线。如图所示，摩擦片接触面综合应力随时间整体呈上升趋势，但局部有应力发生振荡现象；各半径处应力相差较小，应力分布较钢片均匀，盘面内边缘节点1918处平均应力值最大；由于摩擦片内齿与传动轴外齿花键啮合受到的周向力较为集中，在盘面热应力和机械应力共同作用下，综合应力值较大，中间位置温度高造成变形严重，接触不均，综合应力值较小。

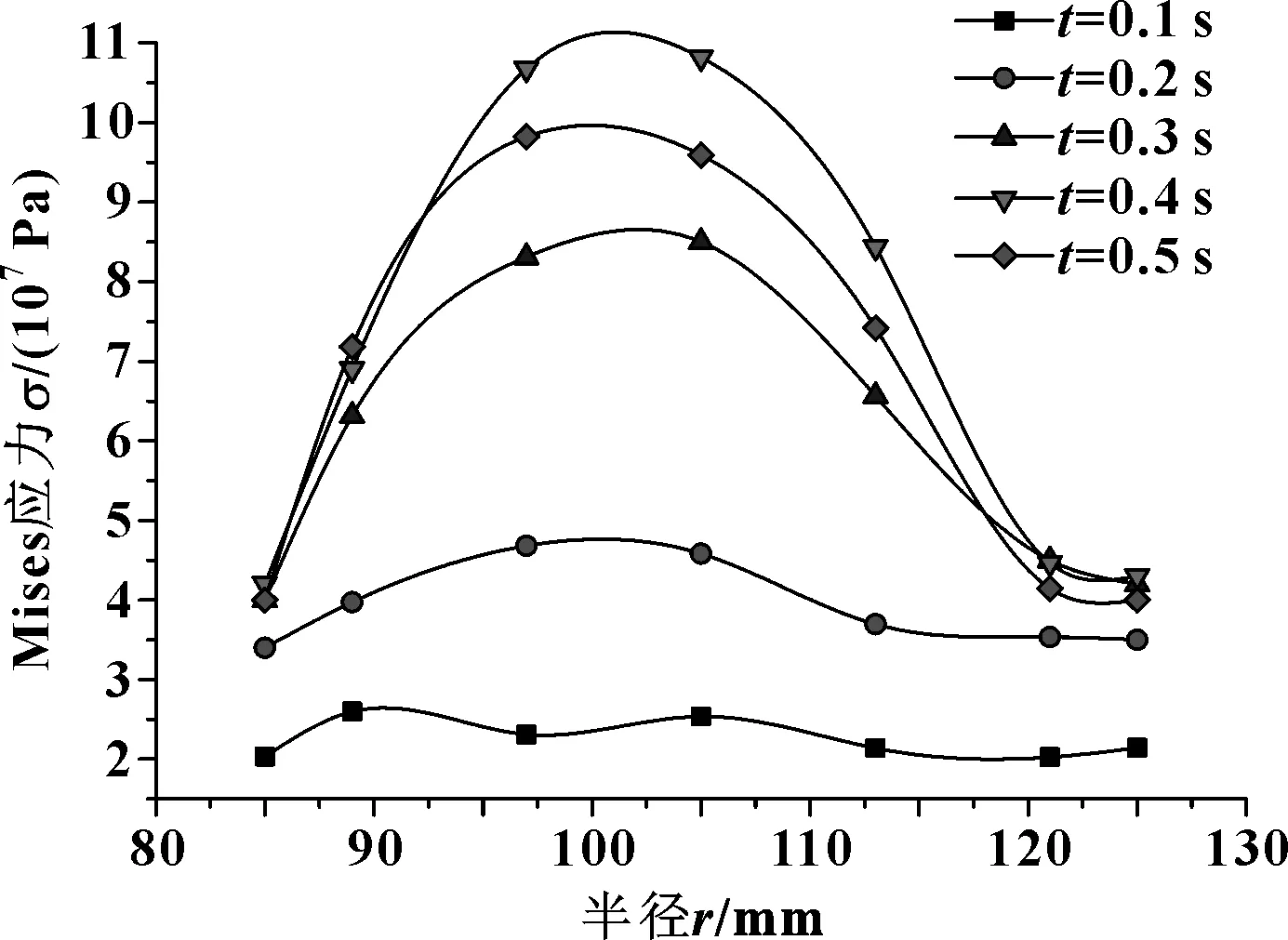
图12 不同时刻钢片应力沿半径分布曲线

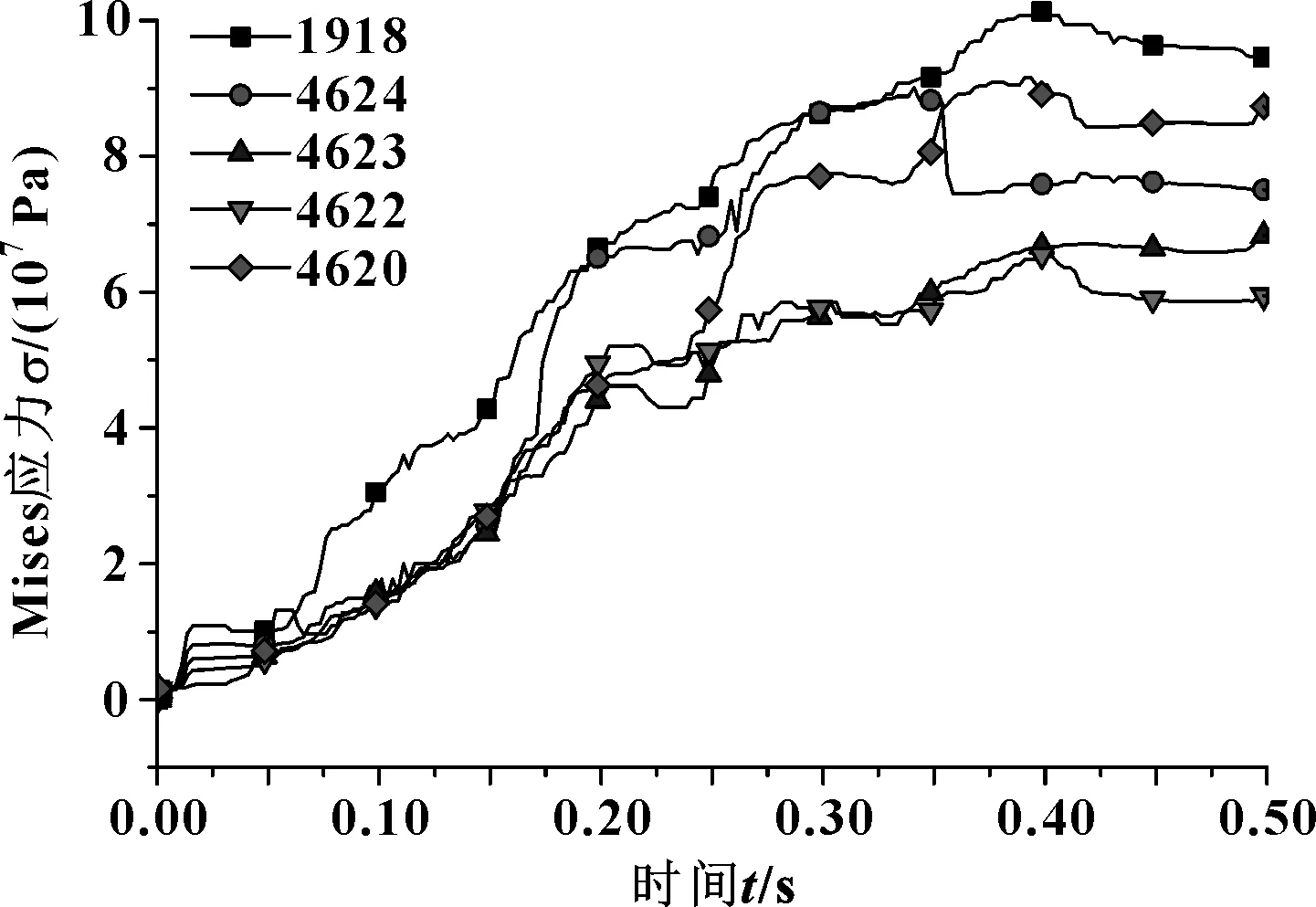
图13 摩擦片模型接触面节点综合应力随时间变化曲线

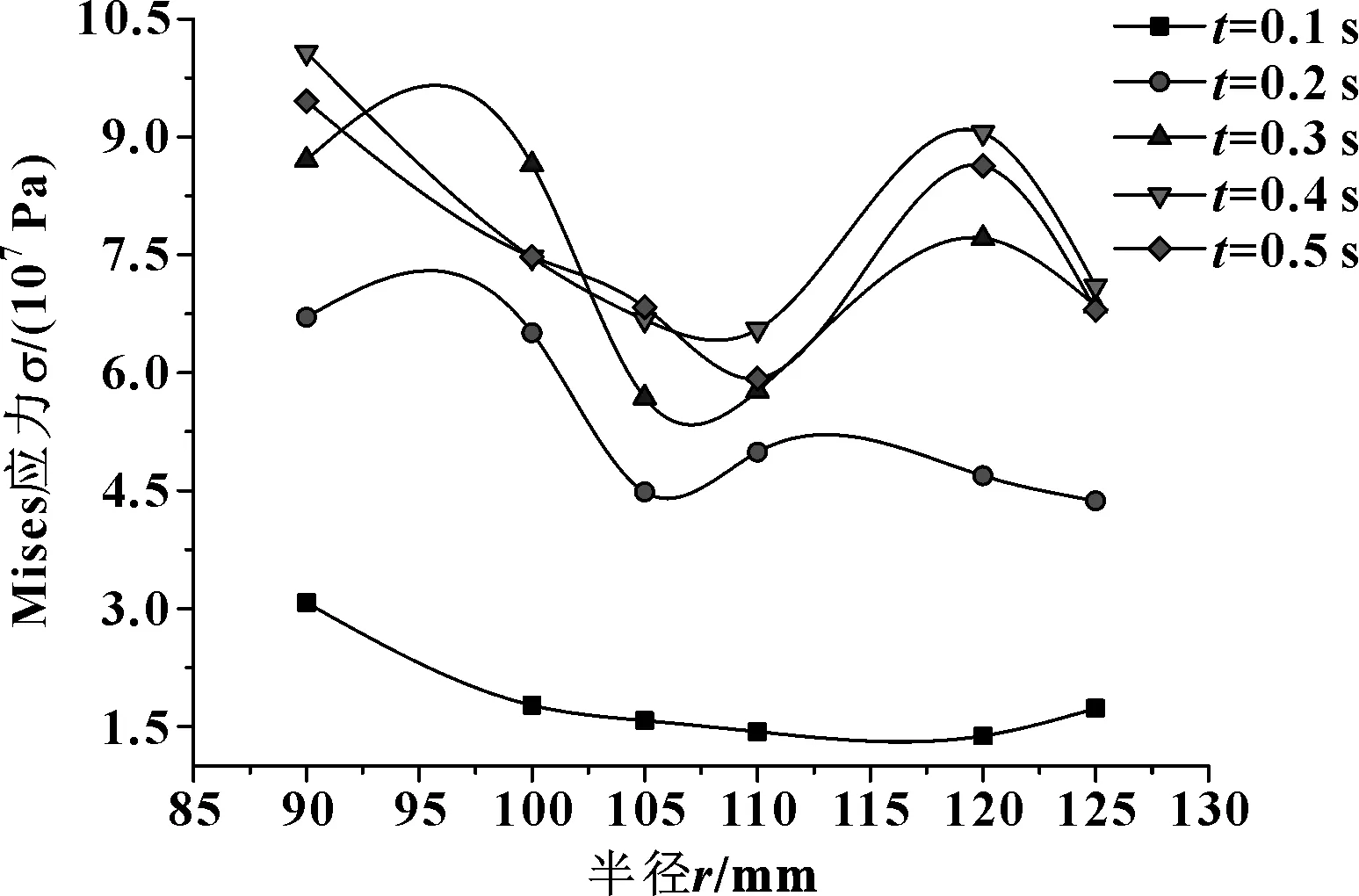
图14 摩擦片模型接触面节点综合应力沿径向分布

2.3 影响因素分析

对偶钢片和摩擦片温度分布类似，且钢片综合应力随温度变化较明显，湿式摩擦副滑摩过程中，钢片材料吸热快易产生高温区，且因盘面热弹不稳定性发生变形和破坏[18]。文中着重分析压力、相对转速和润滑流量对钢片温度场的影响。

2.3.1 压力的影响

有限元模拟过程中设置边界条件：转速差为700 r/min，均布压力分别为0.8、1.4、2.0 MPa，模拟得到的对偶钢片温度场分布如图15和图16所示。图15显示半径106 mm处温度随压力增加的瞬时变化规律，在压力较低时，温度上升缓慢，温度梯度较低；滑摩时间不变，压力增大时，温度上升剧烈，温度梯度也迅速增大，加剧了温度分布不均，促使局部高温区的产生，影响湿式摩擦副的正常工作。

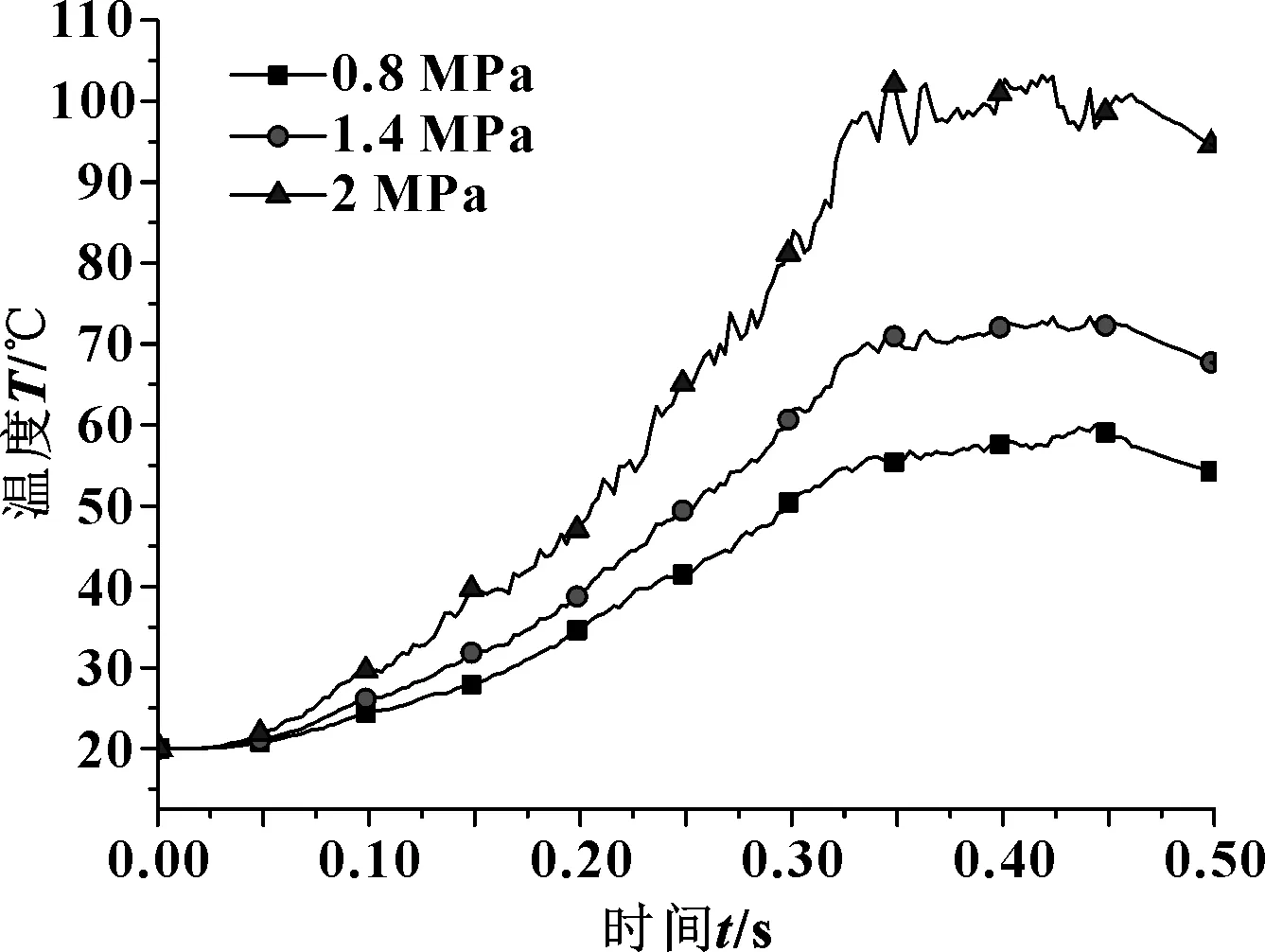
图15 不同接合压力下半径106 mm处钢片温度曲线

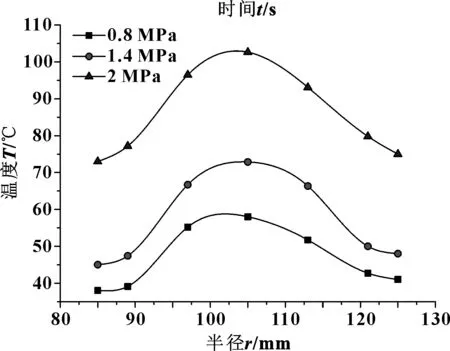
图16 t=0.4 s时不同接合压力下钢片温度沿半径分布曲线

图16表明，压力增大使得整个钢片接触面温度整体上升，且压力由1.4 MPa增长到2.0 MPa造成的盘面温升明显高于压力由0.8 MPa增长到1.4 MPa的温升。较大压力更易增加对偶钢片的热弹不稳定性，易导致摩擦副整体温度上升。

2.3.2 相对转速的影响

压力设置1.40 MPa，分别在摩擦副转速差为500、700、900 r/min下对对偶钢片温度场分布进行有限元模拟。由于对偶钢片在半径106 mm处温度上升最快且温度值最大，是高温区集中出现区域，故选取其温度变化曲线进行对比，如图17所示。

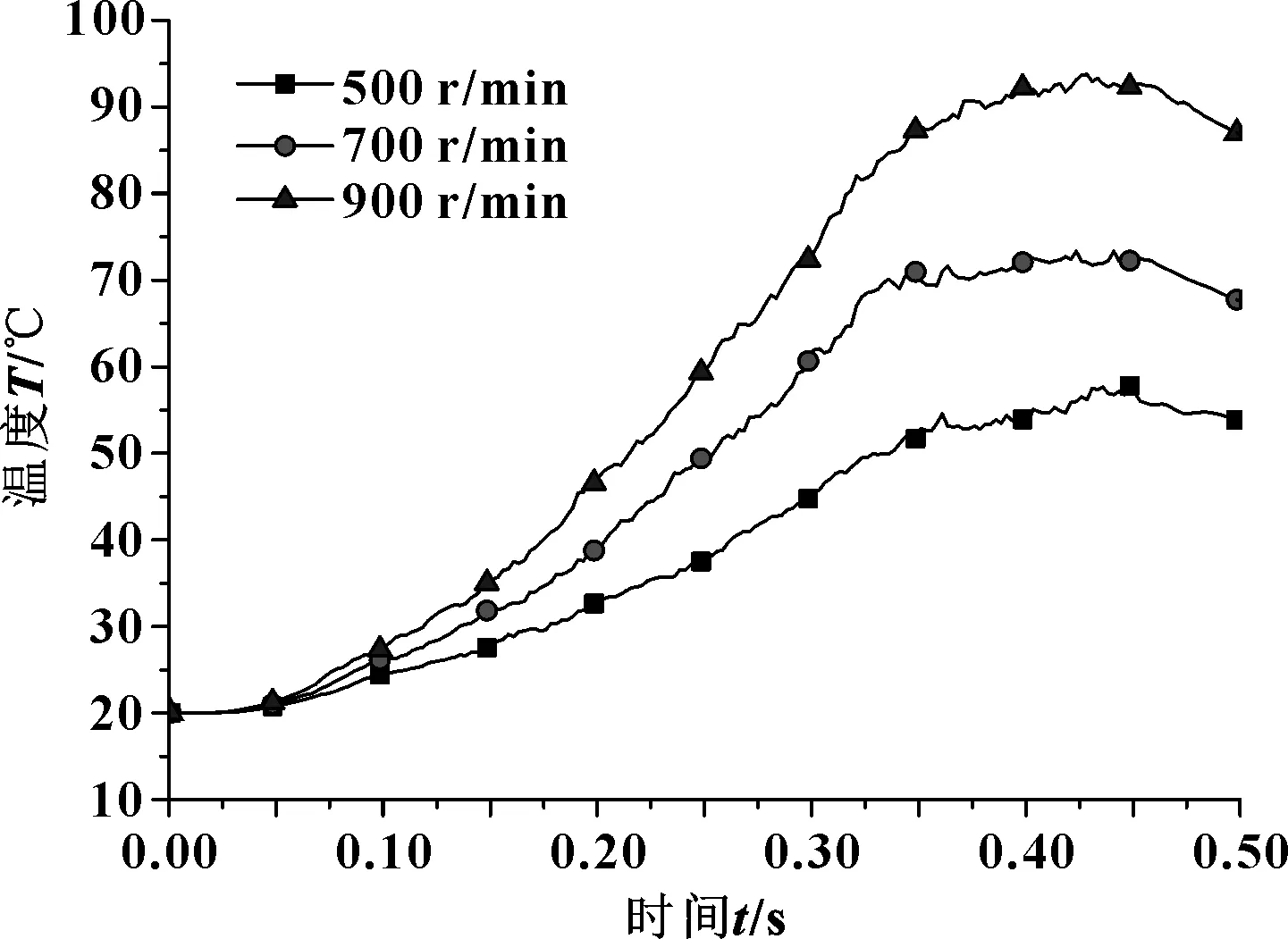
图17 不同转速差下半径106 mm处钢片温度曲线

图17显示，随着滑摩时间的推移，转速差越大温升越高，温度梯度越大。较大的转速差使得摩擦副在滑摩过程中，在短时间内积累大量的热，增加了对偶钢片的热不稳定性，导致易于出现高温点。

图18所示为滑摩时间0.4 s时温度在钢片接触面沿半径分布，此时温度最高，温度梯度也最大；转速差较低时，高温区在中内圆位置100 mm处；随着转速差的增大，高温区外移到半径105 mm处，且转速差越大，径向温度梯度越大。

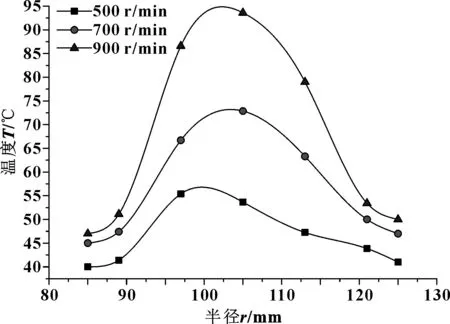
图18 t=0.4 s不同转速差下钢片温度沿半径分布曲线

摩擦副转速越大，产生的热流密度越大，虽然接触面冷却油的对流换热量也会增大，但散热量依然小于产热量，温梯度将增大，因此过高转速易造成摩擦副热失效。

2.3.3 润滑流量的影响

在有限元模型中设置接合压力1.4 MPa，转速差700 r/min，模拟分析不同对流换热条件，湿式摩擦副在乏油润滑、正常润滑、富油润滑3种状态下摩擦副的温度变化曲线，如图19所示。

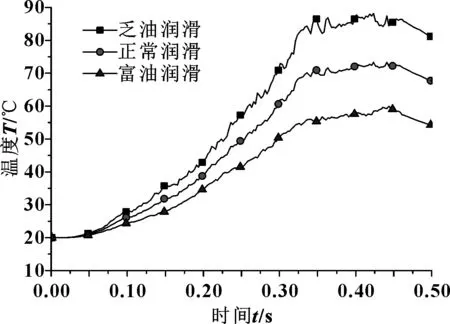
图19 3种润滑状态半径106 mm处温度变化曲线

由图19可知，3种润滑状态温度上升趋势类似，滑摩时间相同的情况下，乏油润滑状态下温升较大，且在0.35～0.4 s之间曲线出现明显抖动，而正常润滑和富油润滑状态下温度到达峰值时相对平稳。这是由于乏油状态对流换热条件较差，摩擦副接触面间摩擦热不断累积，温度显著升高；高温区热应力引起变形，变形改变接触面积，导致局部接触应力增加，引起摩擦热增加，进一步加剧热变形。如此循环，增大热弹不稳定性。

3 温度场测试试验及分析

图20(a)所示为湿式摩擦副试验台，图20(b)为摩擦副测温装置图，图20(c)为温度传感器布置示意图，温度传感器采用响应时间为5 ms的K型热电偶。在湿式摩擦副滑摩过程中，摩擦副处于旋转状态，利用集流环作为热电偶传感器的输出接口，通过PXI6225数据采集卡实时采集温度数据，并在Labview上位机软件中做实时动态监测。

以转速差400 r/min，接合压力1.4 MPa，润滑流量10 L/min为例，对偶钢片接触表面整体温度分布进行测试，结果如图21所示。

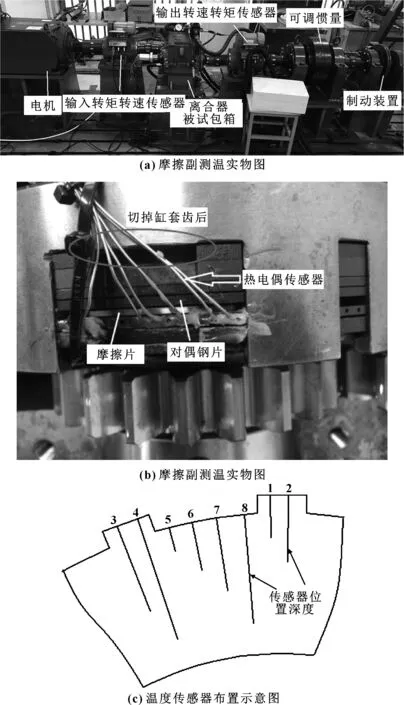
图20 湿式摩擦副试验台及测温系统

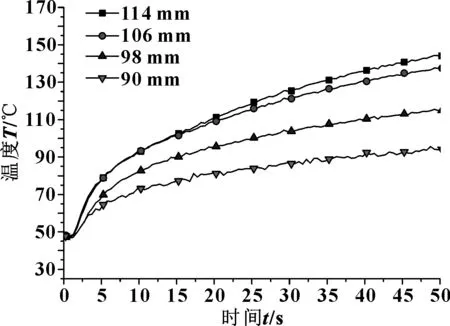
图21 钢片盘面不同半径处温度曲线

图21显示，半径114 mm处温度上升最快，其次中间位置106 mm处，温度向钢片内圆依次递减；滑摩初期盘面温度上升剧烈，5 s后温度持续均匀上升；滑摩时间越长热量积累越多，盘面温升越大；摩擦副滑摩一定时间后各半径处平均温度差值趋于定值。该结论与有限元模拟得到的对偶钢片接触面节点温度变化规律相一致。

图22所示为3种转速下对偶钢片半径106 mm处温度随滑摩时间变化曲线。可以看出：转速差越大温升越快，最大值出现在1.6～1.8 s，温升变化规律与有限元模拟结果类似。

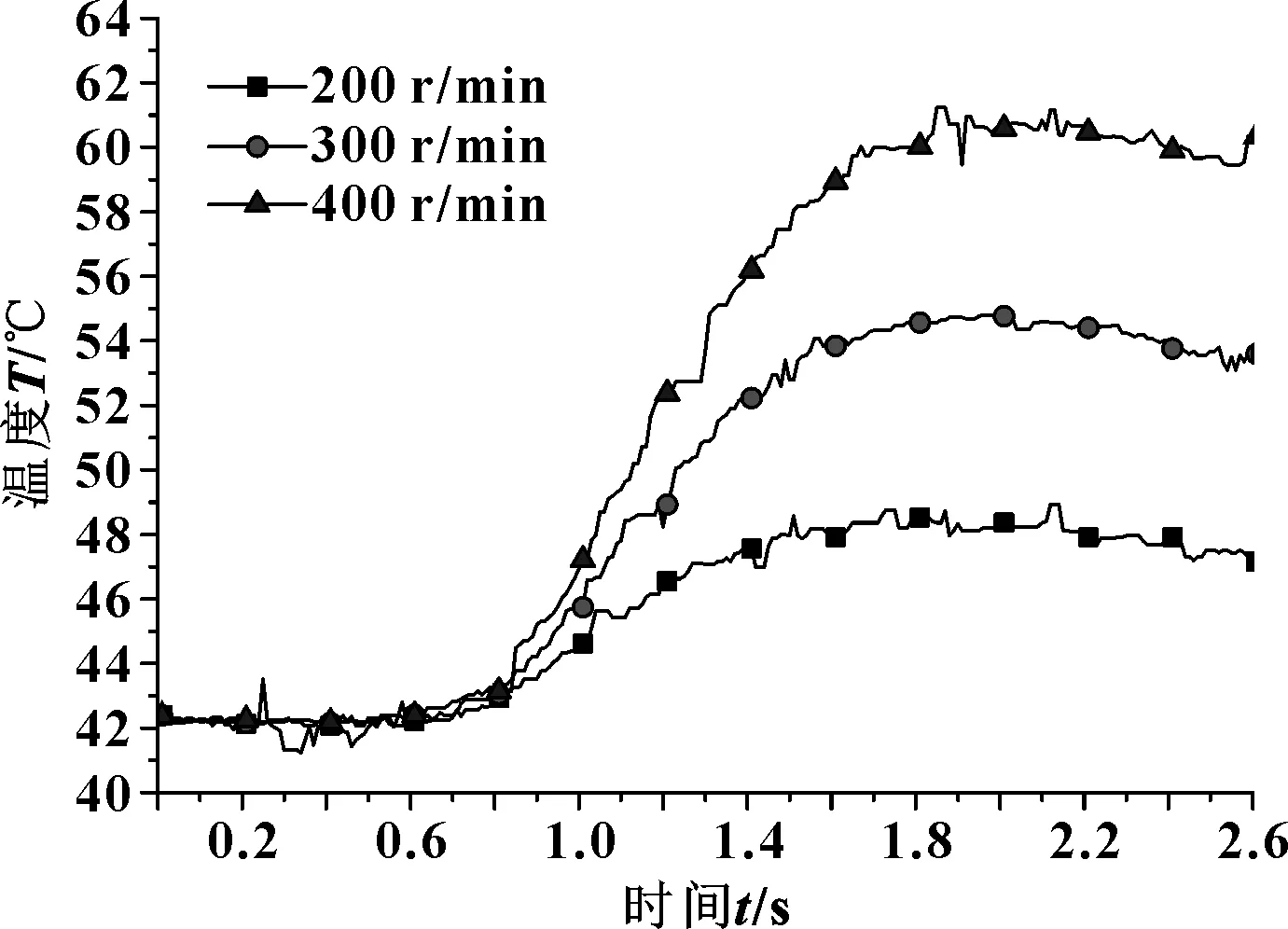
图22 不同转速差下半径106 mm处温度变化曲线

不同转速差下的温升如表5所示。可见，在滑摩转速较低情况下，转速每上升100 r/min，温升值增加30%～50%。

表5 不同转速差下温升

4 结论

(1)对偶钢片和摩擦片均存在沿周向分布的高温环带，且靠近外径侧更易出现高温和应力集中区；对偶钢片相对于摩擦片更易出现温度和应力分布不均匀情况。

(2)摩擦热在滑摩初期不断积累，径向中部位置相对于环面内外边缘处不易散热，容易累积热量导致出现高温环带，且随时间温度持续上升；滑摩后期，随着相对转速的下降，摩擦热生成量随时间下降显著，热量累积量小于散热量，温度逐渐降低。

(3)湿式摩擦副滑摩过程中，温度由外及内依次递减，最大温度随压力增加、相对转速增大、润滑流量减小而增加，并得到试验验证。