基于ANSYS的10 MW风力机叶片弯扭耦合特性研究
VasilisRiziotisGiannisSeferainTohidBagherpour
(1.华中科技大学中欧清洁与可再生能源学院,武汉 430074; 2.华中科技大学能源与动力工程学院,武汉 430074; 3.School of Mechanical Engineering, National Technology University of Athens, 9 HeroonPolytechneiou Street, GR15780 Athens, Greece)
0 引 言
随着风力机发电容量的不断增大,风力机叶片趋于大型化的同时,承受的载荷也越来越大。目前主流叶片都采用复合材料制成。在叶片中引入材料的弯扭耦合(BTC)效应成为一种流行的叶片减载荷方式[1]。弯扭耦合是指当叶片在风载荷作用下,弯曲的同时发生扭转变形的现象。这种现象会导致攻角的改变,减少叶片承受的载荷。该方法是通过改变叶片梁帽上或者表皮上各向异性材料的铺层角度来实现铺层水平上法向应力和剪切应力的耦合,从而引起叶片的弯曲和扭转耦合。
对叶片弯扭耦合的模拟是基于不均匀各向异性梁理论和有限元理论。Blasques等[2]结合Saint-Venant理论开发了二维梁截面特性分析工具BECAS。Bagherpour等[3]采用BECAS结合hGAST(一维各向异性梁分析工具)模拟了叶片的弯扭耦合特性。Fedorov和Berggreen[4]提出弯扭耦合系数计算方法。Hang Meng[5]等使用BECAS和一维各向异性梁模拟在弯扭耦合影响下叶片承受的载荷用于疲劳寿命分析。上述文献都是将3D叶片分为了2D翼型截面和1D梁结合的形式来分析弯扭耦合特性。这种简化的方式将模型置于不同的计算环境,且网格划分稀疏,增大了结果的不确定性。此外当需要通过改变材料铺层角度在叶片中引入弯扭耦合特性时,计算过程繁琐。文中通过建立叶片整体三维有限元模型分析弯扭耦合特性。可有效避免由于计算环境不同带来的误差,且网格划分密集,增加了结果的可靠性。另外直接通过改变参数化编程语言中参数的方式在叶片中引入不同的铺层角度和铺层位置,极大的提高了计算效率。国内在风力机叶片弯扭耦合领域的文献较少,随着海上风电的发展,大容量风力机组已成必然趋势。刘宇航等[6]和安立强[7]等在ANSYS中建立了三维叶片模型,分析了叶片在气动载荷作用下的变形情况。但由于采用的5 MW 叶片数据,翼型截面结构简单,结果不理想。文中采用了最新的DTU 10 MW风力机叶片数据,分析叶片在不同铺层角度下的气动弹性响应和该叶片能够取得的最大扭转变形,弯扭耦合效应明显。为其他研究人员提供参考。
1 有限元模型
1.1 箱形梁有限元模型
叶片具有长宽比,长厚比大的特点,常用箱形梁做初步模拟。文中首先在ANSYS中建立了箱形梁有限元模型,与已有的实验数据和其他数值模拟结果作对比分析。
采用了Chadra[8]实验梁数据。其为薄壁复合材料梁,长0.762 m,恒定的箱型截面,尺寸为13.6*24.2 mm(0.537*0.953 inch ),壁厚7.6 mm(0.03 inch),对称铺层,上下为[45]6,左右为[±45]3,材料为AS4/3501-6单向石墨/环氧树脂,经坐标系转换后完整的材料特性见表1。
表1箱型梁材料特性

材料名称弹性模量/GPa泊松比ExEyEzGxyGxzGyzVxyVxzVyz密度/kg·m-3AS4/3501-61420.810.8166.133.770.30.420.421580
边界条件为一端采用固定约束,另一端加载垂直集中力4.448 N。在ANSYS中选择适用于复合材料建模的shell181单元,它是每个节点具有6个自由度的4节点单元,适用于模拟分层的复合壳或夹层结构。此外需要注意的是,铺层的偏置情况需选择向内偏置。在箱型梁各截面建立中心节点,并通过MPC多点约束方法耦合参考点与截面上各从节点来分析梁的变形情况。
图1展示了ANSYS结果与Chadra的实验解,Stablein和Hansen[9],Smith和Chopra[10]的数值解以及Bagherpour使用一维梁模型和二维截面结合模拟得到的数值结果的对比。在扭转角度上ANSYS很好的捕捉了变化趋势;在弯曲方向上,ANSYS表现出良好的预测能力,相比于其他软件,ANSYS的结果更接近实验解。

图1 梁模型的实验解和数值解
1.2 DTU 10MW 实验风机
该风力机设计风况等级为IEC IA级,为变速变桨距,三叶片风力机,风轮直径为178.3 m,轮毂中心距地面119 m。切入风速为4 m/s,切出风速为25 m/s,额定风速为11.4 m/s,在额定转速9.6rpm下达到10 MW额定输出功率。叶片总长度为89.166 m,从叶根到叶尖共分为101个不同的翼型截面,3个腹板支撑结构。如图2所示每个翼型截面分为11个部分。
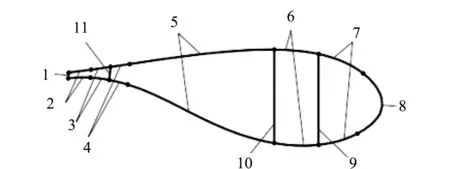
图2 翼型截面示意
叶片由单轴向布,双轴向布,三轴向布和巴沙木四种材料组成,材料特性如表2所示。材料的铺层顺序和厚度以及叶片的预弯和预扭随叶片展向分布可参见文献[11]。关于DTU10 MW风力机的更多参数可参见文献[12]。翼型截面坐标系为X轴沿弦线方向由尾缘指向前缘;Y轴垂直于X轴由吸力面指向压力面,Z轴由叶片根部指向叶尖。载荷计算也将遵循该坐标系。
1.3 建立叶片有限元模型
通过设置材料属性-输入关键点-生成翼型轮廓-生成面-定义铺层-网格划分的步骤建立叶片壳有限元模型。利用参数化设计语言APDL的循环特性实现快速建模。叶片模型共由19569个单元和19007个节点组成,其中包括101个在不同翼型截面位置处建立的MPC主节点。
在叶根加固定约束后,前八阶振型如图3所示,叶片振型从低阶到高阶逐渐复杂,一阶振型为叶片一阶挥舞振动,二阶振型为叶片一阶摆振振动,三阶振型为二阶挥舞振动,四阶振型为二阶摆振振动,五阶振型为三阶挥舞振动,六阶振型为一阶扭转振动,七阶振型为高阶摆振振动,八阶振型为高阶挥舞振动。

图3 叶片前八阶振型
对应的固有频率与其他模拟空气弹性变形工具的结果[13]作对比,见表3。其中hGAST,NEREA,Cp-Lambda,HAWC2采用的是梁理论,NISA是三维有限元模型。可见ANSYS的模拟结果与其他软件结果具有良好的一致性。
表2叶片材料特性
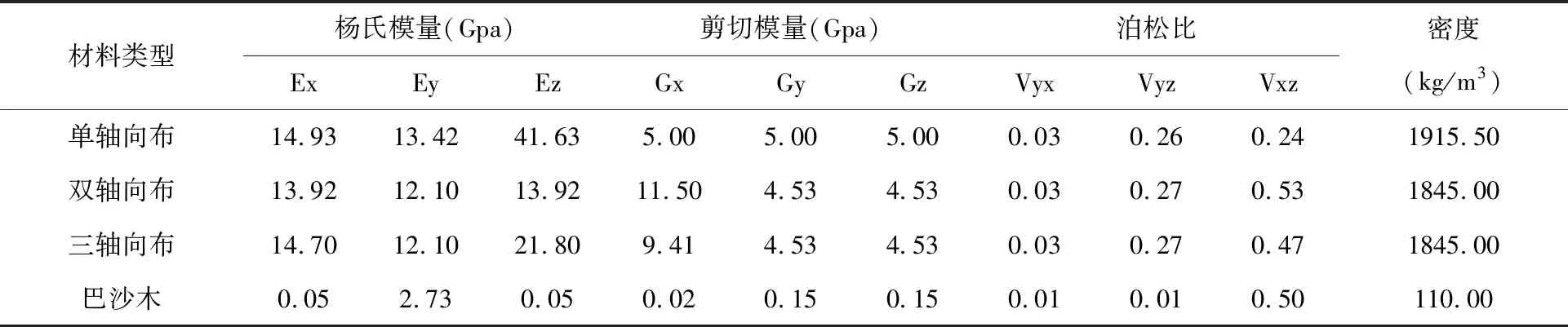
材料类型杨氏模量(Gpa)剪切模量(Gpa)泊松比ExEyEzGxGyGzVyxVyzVxz密度(kg/m3)单轴向布14.9313.4241.635.005.005.000.030.260.241915.50双轴向布13.9212.1013.9211.504.534.530.030.270.531845.00三轴向布14.7012.1021.809.414.534.530.030.270.471845.00巴沙木0.052.730.050.020.150.150.010.010.50110.00
表3叶片固有频率对比
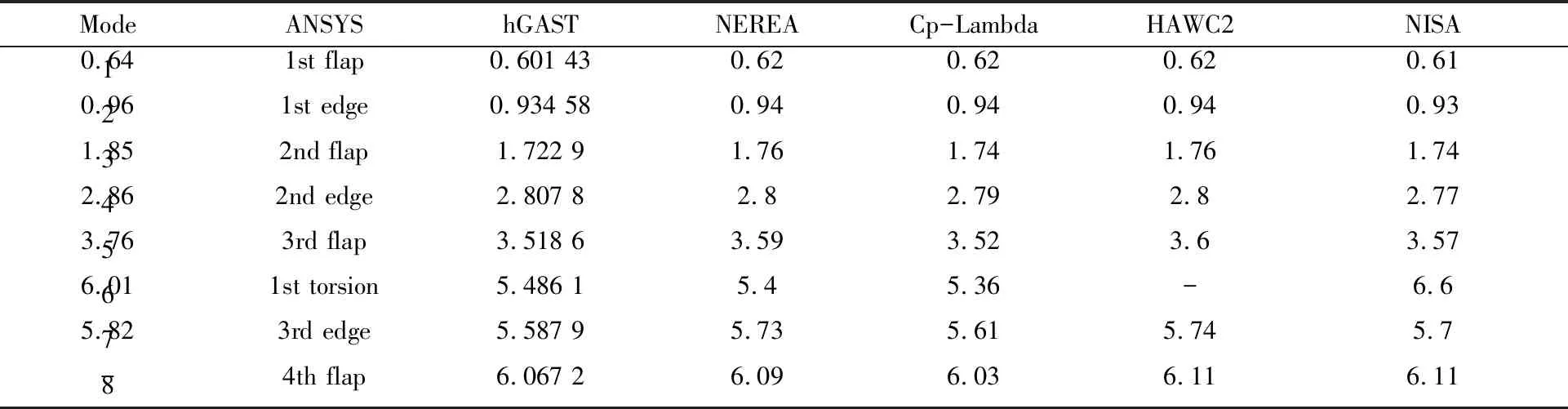
ModeANSYShGASTNEREACp-LambdaHAWC2NISA11st flap0.601 430.620.620.620.610.6421st edge0.934 580.940.940.940.930.9632nd flap1.722 91.761.741.761.741.8542nd edge2.807 82.82.792.82.772.8653rd flap3.518 63.593.523.63.573.7661st torsion5.486 15.45.36-6.66.0173rd edge5.587 95.735.615.745.75.8284th flap6.067 26.096.036.116.11-
2 叶片的弯扭耦合特性
通过改变梁帽位置单轴向布的铺层角度在叶片结构中引入弯扭耦合。铺层角度在叶片上下表面对称分布。计算叶片在11.4 m/s额定风速下,即风力机正常发电工况下叶片的弯曲和扭转变形情况,其中风为稳态风。
通过叶素动量理论(BEM)和叶片变形量迭代得到叶片受到的气动载荷。过程如下:首先在ANSYS中输入一个初始载荷,之后将对应的叶片变形输入BEM程序得到新的载荷,重复该过程直到叶片变形稳定,得到该叶片变形下对应的载荷。铺层角度为0度和10度条件下叶片受到的气动载荷设为载荷1和载荷2,如图4所示。气动载荷在叶根区域较小,沿着叶展方向逐渐增大,接近叶尖位置时急速下降。载荷1和载荷2均为均布载荷,经过式1转化为集中力后通过MPC节点耦合的方式施加到叶片壳有限元模型的101个截面上。
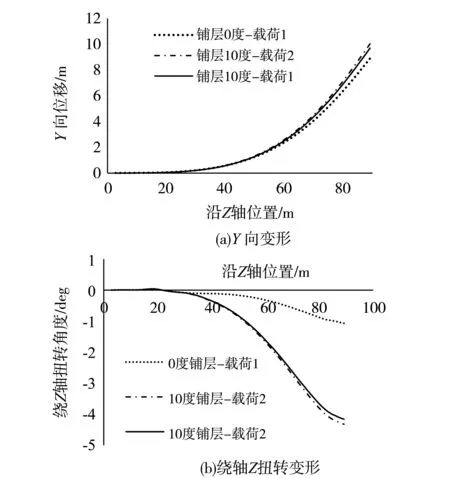
设截面i距叶根距离为X,受到的集中力为F,则:
(1)
其中,(0 图4 额定风况下气动载荷 图5展示了叶片在0度铺层下的变形情况及10度铺层下加载载荷1和载荷2得到的弯扭变形。叶片的弯扭变形连续,沿着叶展方向不断增大,在叶尖达到最大值。在额定风速下,0度铺层叶片叶尖弯曲变形为8.89m,扭转变形为1.06度。10度铺层叶片在载荷2作用下,叶尖弯曲变形为9.68m,扭转变形为4.16度。10度铺层叶片在两种情况下叶尖最大扭转角度误差为3.6%。由于计算载荷的迭代过程复杂,接下来的计算将直接采用在0度铺层条件下的载荷。 图5 叶片在0度铺层和10度铺层下变形 由于材料铺层角度和耦合区域的不同会影响叶片的弯扭耦合性能。这里设定叶尖扭转角度在2度到6度以0.5度的间隔变化,通过改变铺层角度和起始位置的不同组合以得到预期的叶尖扭转角度。选定铺层起始位置为0%,20%,35%或50%,结果如图6所示。从图中可以看到耦合区域越靠近叶尖,达到指定的叶尖扭转角度需要的铺层角度越大;弯扭耦合系数在铺层角度为18.5度之后下降;可达到的最大叶尖扭转变形为6度。这表明如果继续增大铺层角度,不会造成叶片扭转变形的继续增大,从而不会造成叶片载荷的降低。为设计具有优良弯扭耦合性能的叶片提供参考。 图6 弯扭耦合特性图 (1)在ANSYS里选用shell 181单元建立箱形梁模型,改变梁表面材料铺层角度,梁在自由端集中力作用下的变形与已有的实验结果和数值结果基本一致。在弯曲变形上ANSYS模拟结果更接近实验结果。 (2)建立了10 MW叶片壳有限元模型,通过改变梁帽位置材料铺层角度在叶片中引入弯扭耦合效应。由于采用参数化设计语言,在快速实现模型建立之外,还极大的方便了模型参数的修改,例如铺层角度和耦合位置的改变,极大的提高了计算效率。 (3)通过绘制弯扭耦合特性图发现叶片的扭转变形不会随着铺层角度的增大而无限增大,为设计具有优良气动弹性裁剪性能的叶片提供参考。 (4)文中模拟了叶片在弯扭耦合作用下的变形情况,没有涉及叶片载荷量的计算,接下来可在这一方面继续研究。此外,由于载荷的降低,在叶片疲劳失效范围内可以考虑减少叶片材料,达到经济性的目的。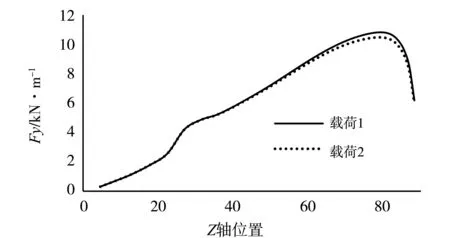
3 结束语

