扩展有限元法在疲劳裂纹扩展模拟中的应用

摘  要：随着计算机技术的发展，有限元仿真技术被大量应用于疲劳计算中。然而，在进行疲劳分析时，常规有限元法往往对于网格的划分限制较大，工作量大，效率低。文章采用扩展有限元法对疲劳裂纹扩展进行仿真分析，简化了网格划分过程，并通过与试验结果的对比，证明了该方法的准确性。

关键词：扩展有限元;疲劳裂纹扩展;仿真分析

中图分类号：O346.1        文献标志码：A 文章编号：2095-2945（2019）18-0011-03

Abstract： With the development of computer technology， finite element simulation technology is widely used in fatigue calculation. However， in the fatigue analysis， the conventional finite element method often has great restrictions on the division of grid， heavy workload and low efficiency. In this paper， the fatigue crack growth is simulated and analyzed using the Extended Finite Element Method （XFEM）， the process of meshing is simplified， and the accuracy of the method is proved by comparing with the experimental results.

Keywords： Extended Finite Element Method （XFEM）; fatigue crack growth; simulation analysis

前言

目前，有限元仿真大量应用于疲劳问题分析计算中。然而常规有限元法采用连续函数作为形状（插值）函数，在单元内部形状函数和材料性能必须保证连续，进行裂纹分析时，裂纹面需与网格边界重合，网格节点需与间断面的尖端重合[1-2]。如Abaqus中针对裂纹扩展分析的两种技术：基于debond裂纹扩展技术和基于cohesive裂纹扩展技术。两种技术均需提前指定裂纹扩展区域与方向，对于网格的划分限制较大，工作量大，效率低。

而在扩展有限元法（Extended Finite Element Method，XFEM）中，网格与结构内部的几何或物理界面无关，两者间相互独立，裂纹尖端应力场的计算与裂纹面扩展计算相互独立，避免了在裂纹尖端进行高密度网格划分的问题和网格重新划分的工作[3-5]。

本文采用扩展有限元法对疲劳裂纹扩展进行仿真分析，达到无需指定裂纹扩展路径、无需进行高密网格划分也可模拟裂纹扩展的目的，节省建模所需要的时间，大大减少工作量，同时又提高了裂纹扩展模拟的准确度。

1 扩展有限元法理论基础

1.1 单位分解法（PUM）

扩展有限元通过在常规有限元位移模式中加进跳跃函数和渐进裂尖位移场函数等一些特殊的函数，来有效地模拟类似裂纹一类的强不连续问题，而它的理论基础既为单位分解法。

两种不同网格划分形式下应力强度因子见表1，表2。

由表1和表2的对比可以发现，两种网格划分方式得到的应力强度因子都能较好的吻合应力强度因子的理论解。但裂纹穿透网格时比裂纹沿网格分布时更接近于理论解。

随着网格划分密度的加大，XFEM计算得到的應力强度因子值逐渐接近理论解，当网格密度达到一定程度时，网格密度变化几乎不再对应力强度因子计算结果产生影响，此时XFEM计算不同奇数网格划分的裂纹所得应力强度因子与理论解相对误差为0.79%。

3 疲劳裂纹扩展寿命仿真计算

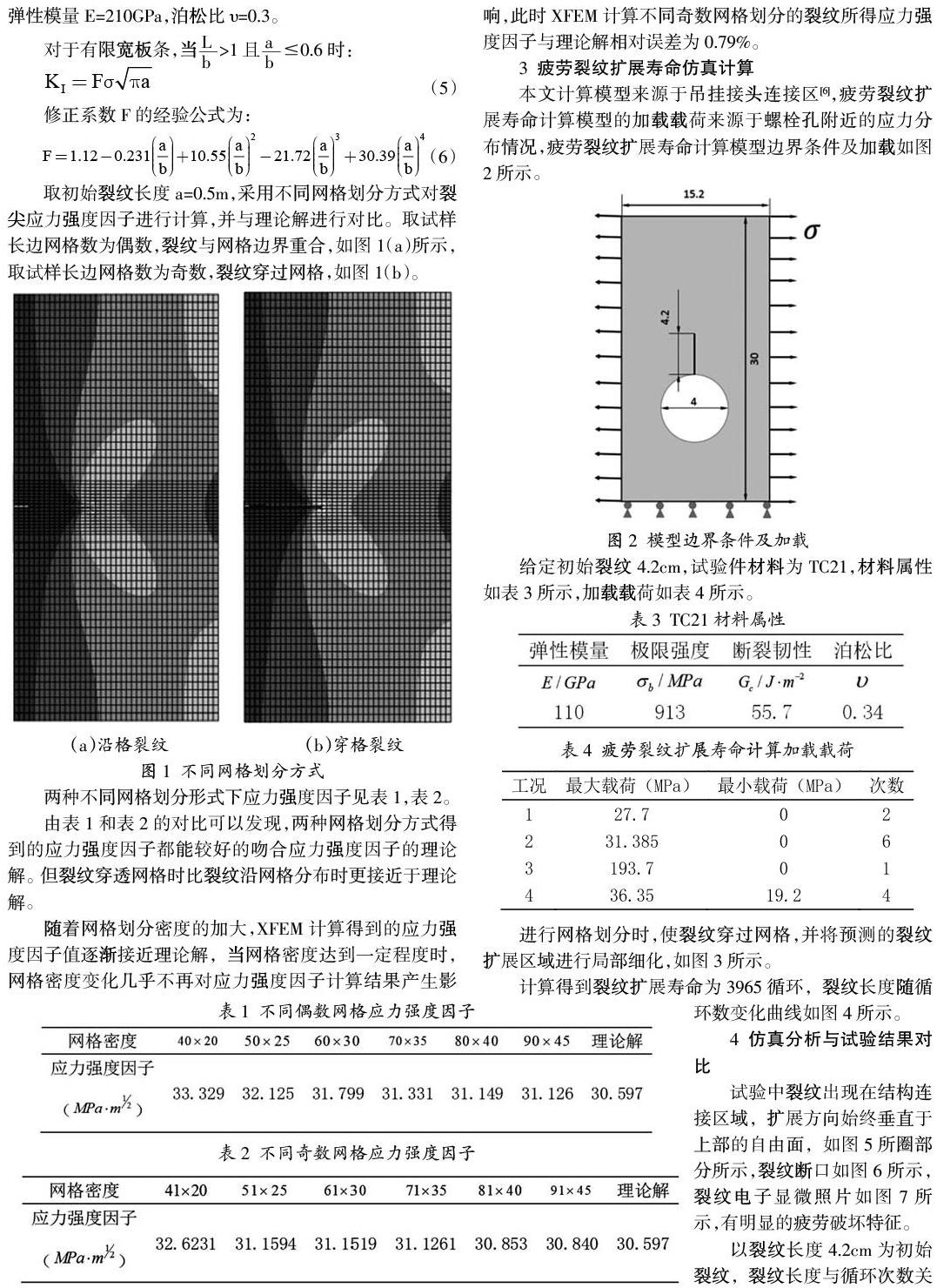
本文计算模型来源于吊挂接头连接区[6]，疲劳裂纹扩展寿命计算模型的加载载荷来源于螺栓孔附近的应力分布情况，疲劳裂纹扩展寿命计算模型边界条件及加载如图2所示。

给定初始裂纹4.2cm，试验件材料为TC21，材料属性如表3所示，加载载荷如表4所示。

进行网格划分时，使裂纹穿过网格，并将预测的裂纹扩展区域进行局部细化，如图3所示。

计算得到裂纹扩展寿命为3965循环，裂纹长度随循环数变化曲线如图4所示。

4 仿真分析与试验结果对比

试验中裂纹出现在结构连接区域，扩展方向始终垂直于上部的自由面，如图5所圈部分所示，裂纹断口如图6所示，裂纹电子显微照片如图7所示，有明显的疲劳破坏特征。

以裂纹长度4.2cm为初始裂纹，裂纹长度与循环次数关系如图8所示。

将用扩展有限元方法得到的疲劳裂纹扩展寿命计算结果与试验得到的结果进行比较，如图9所示。

由图9可以看出，XFEM计算结果与试验结果有较好的吻合性。

5 结束语

仿真分析结果与试验结果吻合性较好，证明了扩展有限元法的网格适应性，即无需在裂纹尖端进行高密度网格划分和网格重新划分的工作，本文所用方法具有工程适用性。

尽管扩展有限元法在解决裂纹扩展问题时简便高效，但仍有一定的限制，在使用时应注意以下事项：

（1）理论上扩展有限元法无进行高密网格划分，但通过细化裂纹区域网格仍可以提高仿真结果准确度。

（2）扩展有限元方法计算疲劳裂纹扩展寿命时，试件需采用同种网格划分，否则无法进行有限元分析计算。

（3）扩展有限元方法更适用于低周疲劳分析，在进行高周疲劳分析时，其适用性较差，结果误差较大。

（4）在Abaqus中，扩展有限元的操作不能完全在CAE中实现，需通过在inp文件中进行关键字的编辑或编写子程序实现。

参考文献：

[1]茹忠亮，朱传锐，张友良，等.断裂问题的扩展有限元法研究[J].岩土力学，2011，32（7）：2171-2176.

[2]余天堂.扩展有限元法的数值方面[J].岩土力学，2007（s1）：305-310.

[3]Belytschko T， Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering. 1999，45（5）：601-620.

[4]Mos， Nicolas， Dolbow J， Belytschko T. A finite element method for crack growth without remeshing [J]. International Journal for Numerical Methods in Engineering. 2015，46（1）：131-150. [5]Sukumar N， Prévost J H. Modeling quasi-static crack growth with the extended finite element method Part I： Computer implementation[J]. International Journal of Solids and Structures. 2003，40（26）：7513-7537.

[6]苟文选，张芮晨，耿小亮，等.一种先进的飞机吊挂结构疲劳寿命仿真分析方法[J].西北工业大学学报，2017（5）.