高精度大天线拼接式钢带光栅编码器测角误差分析与修正研究
刘波
摘 要:目前由于毫米波及亚毫米波频段天文观测的需要,国际上新建了很多高精度的毫米波射电望远镜,发布了很多最新科学成果。如EHT最近发布黑洞成像,验证了爱因斯坦的广义相对论,参与观测的6个站点8个台站,均可在毫米波频段观测,虽然我国也为此次成果做出突出贡献,但8台望远镜均为国外研制生产,因此研制高精度的大型射电望远镜迫在眉睫。高精度的大型射电望远镜最为大型装备,涉及多个领域关键技术突破,如测角精度就是实现核心指标跟踪和指向精度至为关键的重要基础。本文根据现有科学和工程领域的最新成果和产品,从影响测角误差的因素进行分析,论证了拼接钢带光栅尺作为角度编码器的性能可以满足指标需要,为未来大口径天线设计阶段的测角方案分析和分配、预估测角精度,为降低设计和加工误差提供参考。
关键词:测角精度;射电望远镜;天线;伺服控制;光栅尺拼接
中图分类号:TN762 文献标识码:A 文章编号:1671-2064(2019)10-0055-02
0 引言
由于亚毫米波射电望远镜指向精度高,对伺服系统编码器的测角精度提出了苛刻的要求。如某项目的跟踪和指向精度指标要求为0.5″,以目前工程普遍采用的旋变和角度编码器均无法满足指标要求。因此,必须采用拼接钢带光栅尺作为角度编码器。拼接式钢带光栅编码器具备精度高、装调简单,且能灵活调整自身尺寸的优点,将作为现代大型望远镜测角系统新一代测角编码器[1,2]。
编码器的测角误差主要来源于光栅尺的系统误差和机械安装误差等周期性误差[3],温度不均匀引起的光栅尺不规则变形对测角误差影响较小,可忽略不计[3,4]。
光栅的刻划误差,指刻划实际位置与理想位置的差值,代表了光栅的质量,影响因素包括光栅的一致性、光栅的栅距、光栅与其基体的相互位置关系。刻划误差由在理想条件下通过批量生产的读数头在信号周期整数倍位置处测量的位置误差确定。
细分误差代表读数头扫描质量,由细分信号的非正交误差、不等幅误差、直流电平漂移误差等引起。目前大多数读数头都是数字化细分,因此也表征信号处理电子电路质量。影响细分的因素有信号周期长度、光栅一致性和光栅栅距、传感器的特性、信号后续处理的稳定性和动态性能。
机械安装误差分为光栅尺(读数头)安装误差和支撑体结构误差2个部分,其中支撑体结构误差包括安装圆盘的偏心、不圆、轴向跳动、径向跳动等。
下面我们对每个误差源进行分析,根据分析结果核算天线测角误差。
1 误差分析与修正
1.1 系统误差的分析和修正
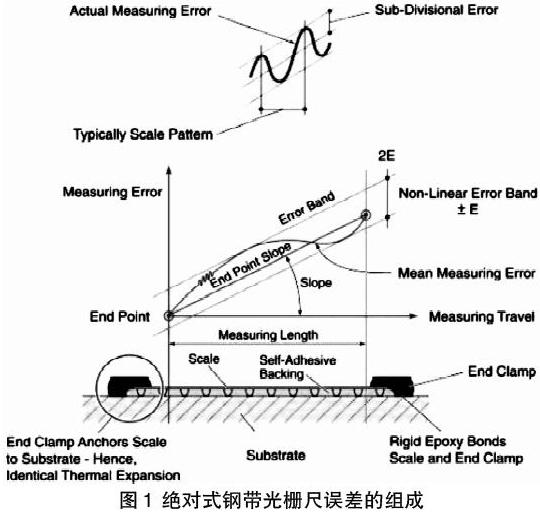
刻划误差和细分误差(SDE)组成系统误差。图1为RENISHAW(雷尼绍)RTLA系列绝对式钢带光栅尺系统误差的组成,从中看出,系统误差包括线性误差和非线性误差。
用于拼接的绝对式高精度栅尺,单根最大长度为21m,分辨率为50nm,刻划精度(包括斜度和线性精度)为±5μm/m。单根光栅尺拼接后作为角度编码器理想精度为6.48″,且从计算过程可知,精度与长度无关。
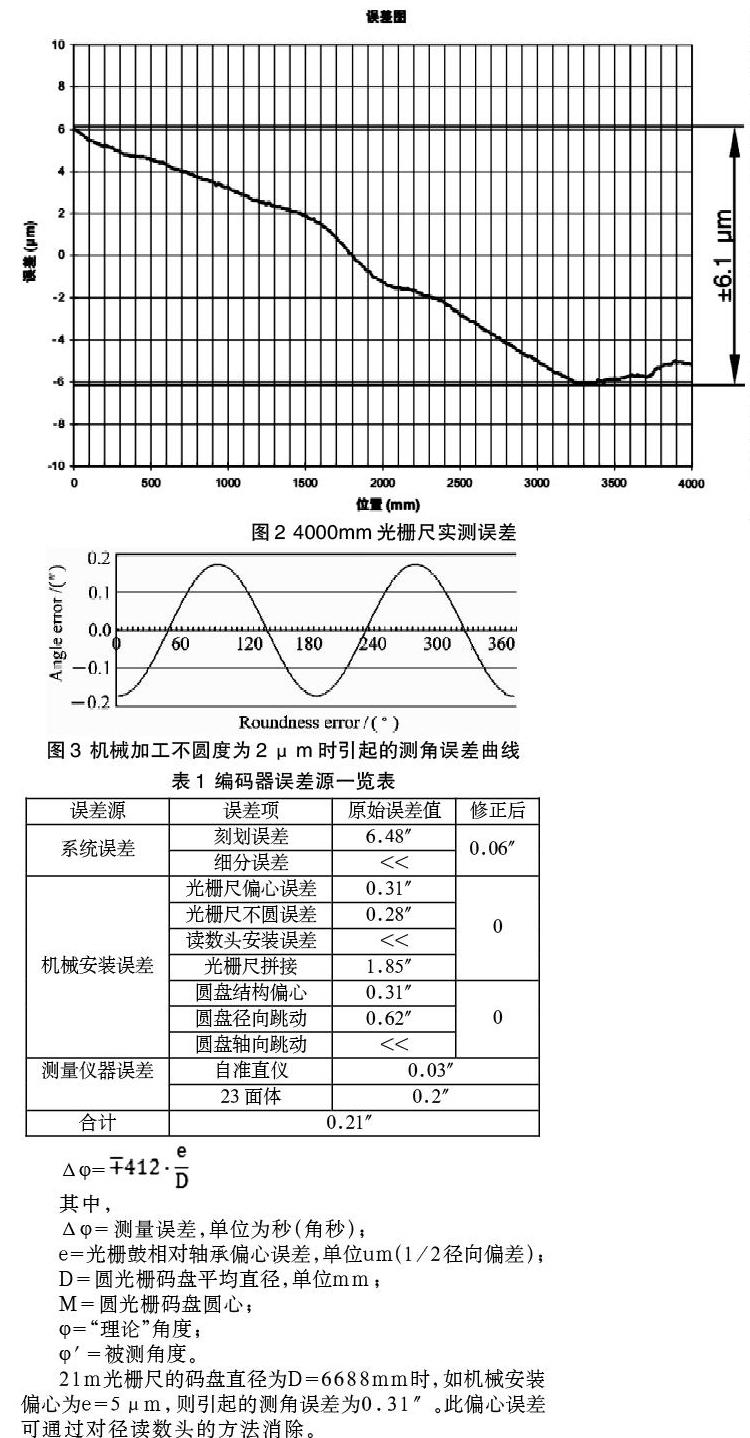
图2是长度为4000mm雷尼绍光栅尺的实测误差曲线[5],如对其进行线性拟合修正,非线性的误差小于1μm,21m光栅尺的非线性误差为10μm,以相同特性来分析,拼接后误差为0.06″。线性误差可以通过线性模型直接消除,非线性模型修正,修正效果取决于算法精度,如果采用准确的非线性模型修正,精度可进一步提高。
RESOLUTE读数头的细分误差为±40nm,信号抖动为10nm RMS,对系统误差的影响忽略。
1.2 机械安装误差分析与修正
机械安装误差的分为光栅尺安装误差和支撑结构体误差,其中光栅尺安装误差又包括读数头安装误差和光栅尺安装误差。
读数头与光栅尺基体之间的扫描间隙有变化时,信号幅值只有轻微变化,只影响单信号周期内位置误差,通过光栅尺编码器自身设计可以保证单信号周期内误差为信号周期的±1%,因此读数头的安装误差可以忽略。
光栅尺粘贴安装时,按压厚度不均、粘贴位置偏离理想位置会引起偏心和不圆误差。
偏心为钢带光栅尺安装后,钢带安装盘的几何中心与实际旋转中心之间的距离[6]。
21m光栅尺的码盘直径为D=6688mm时,如机械安装偏心为e=5μm,则引起的测角误差为0.31″。此偏心误差可通过对径读数头的方法消除。
光栅尺安装不圆误差,推导原理见文献[3],其在实验中采用直径D=458.112mm的拼接光栅尺,不圆度为2μm引起的测角误差为0.18″,实验结果如图3所示,对于D=6688mm的拼接光栅尺,设不圆度为5μm,那么引起的测角误差小于0.28″。从图中也看出,转台旋转一周时不圆度引起的测角误差具有二次谐波特性,因此可通过相位差为90°的两个读数头消除其引起的误差。
光栅尺首尾对接可用力矩扳手确保光栅尺接缝良好,经过试验,对接后正常使用,误差为1个栅距1.85″,此误差可以通过对径消除。
结构误差包括支撑圆盘的偏心、不圆及轴、径向跳动等引起的误差。
偏心误差和上面光栅安装偏心同,误差为0.31″,径向偏心跳动为0.62″,轴向跳动只会引起读数头输出信号的幅值发生变化,不会产生测角误差[4]。其中径向误差对测角的影响分别为0.62″,而光栅尺的安装公差为±150μm间隙、±0.5°扭摆,因此该误差是可以容忍的。
消除上述机械安装误差的方法是沿光栅码盘等距位置安装2个或更多(4个)个读数头[7,8],然后在后续电子电路通过数学方法合并各个位置值。利用相位差為90°的均布4读数头测角方式,采用4读数头消差技术,可消除由轴系跳动、光栅安装偏心和圆度等加工、安装引起的中低频测角误差,且具有实时补偿性,所有偏心误差(安装误差导致的可重复误差,轴承径向偏心导致的不可重复误差)以及光栅误差的所有非均匀谐波都可以清除[7,8]。
测量时,将23面体安装在转台上,通过自准直测量法,测出测角误差。目前德国MOLLER公司的ELCOMATHR型自准直仪器的测量精度为0.03″,23面体自身的测量精度为0.2″。
除了上述的提到的修正算法,安装导致的光栅变形,如形状、基准面,光栅尺相对安装面的位置等都通过编码器的设计确保安装和使用过程中对编码器精度基本没有影响[6]。
误差核算的结果如表1所示,从理论计算结果来看,是满足方案需求的,且通过改进修正算法,上述误差核算值还有优化的余量。
2 结语
本文采用相位差为90°的均布4读数头测角方式,利用4读数头消差技术、和相关文献的实验结果,理论分析了消除了拼接光栅机械安装偏心、圆度误差等对编码器测角的影响,通过核算得出本编码器的性能可以满足方案需要,为未来大口径天线设计阶段的测角方案分析和分配、预估测角精度,为降低设计和加工误差提供参考。
参考文献
[1] 黄龙,潘年,马文礼,等.拼接式编码器测角误差分析及试验[J].中国光学,2015,8(03):464-470.
[2] 韦湘宜,丁红昌,曹国华.光电编码器检测技术的研究现状及发展趋势[J].电子科技,2015,28(09):184-188.
[3] 潘年,马文礼.拼接式钢带光栅编码器测角误差分析与修正[J].中国光学,2013,6(05):788-794.
[4] 赵人杰,马文礼.利用误差谐波补偿法提高金属圆光栅测角精度[J].仪器仪表用户,2009,16(03):69-71.
[5] 雷尼绍RTLA高精度绝对式直线光栅系统规格手册[K].2018,1.
[6] 海德汉角度编码器手册(无内置轴承)[K].2014,6.
[7] 邹自强.论圆光栅多头读数系统[J].光学机械,1983(02):39-48.
[8] 张玉莲.传感器与自动检测技术[M].北京:机械工业出版社,2012.
——多功能毫米波天线

