基于改进卡尔曼滤波的锂电池SOC估算研究

钱潇潇 张菁 杨勇

摘 要：针对新能源汽车的驱动锂电池的剩余电量（SOC）估算，在对传统和新型SOC估算算法进行研究分析的基础上，讨论了卡尔曼滤波算法的运行机理，将其改进变换成拓展卡尔曼滤波算法（EKF）后同锂电池PNGV电路模型相结合对锂电池进行SOC估算。来弥补传统安时法在实际应用中随着估算时间增加而误差增大的缺点。接下来将本文的SOC联合估算算法同传统Ah方法进行综合比较，通过Matlab/Simulink中建立电池的综合仿真模型对SOC算法进行评估和仿真，对其准确性进行验证，证明了算法在面对噪声干扰时比传统的SOC估算算法具有更好鲁棒性和准确性。

关键词： 剩余电量;SOC;卡尔曼滤波;安时法;PNGV模型

文章编号： 2095-2163（2019）03-0194-05 中图分类号： TM912 文献标志码： A

0 引 言

随着经济的增长，汽车市场不断蓬勃发展，传统燃油汽车的使用随即也加剧了能源危机和环境污染。世界各国相继公布燃油车禁售时间，各大汽车厂商都在积极投入研发新能源汽车用来取代传统燃油汽车。锂电池以其无污染、高能量比、循环寿命长等优点被广泛使用在新能源汽车中，作为其核心驱动零部件。对电动汽车而言，如何安全、有效、正确地使用锂电池至关重要。其中，锂电池的电荷状态（state of charge，SOC）实时准确估算是电动汽车的关键技术之一[1]。对于电动汽车来说，动力电池的SOC就好比燃油汽车的剩余油量，是电动汽车重要的性能参数之一，该参数的实时精确估算是整车控制策略的基础，不仅可以提高稳定性和行车安全，同时准确的SOC估算还能防止电池过充过放，延长自身寿命，提高利用率。此外，SOC的正确估算还关系到电池后续的充放电均衡控制和优化管理。

现如今，学者们已经提出各式各样的锂电池SOC估算算法。其中，开路电压法精确、简单易操作，但其缺点是需要电池长时间静置才能得到开路电压，无法满足SOC估算的实时性;安时积分法能够满足实时性，但是只能在短时间内精确估算，随着时间的增加，误差会逐渐加大，同时也存在着初值难以获取的情况。神经网络方法虽然精确，也能满足实时性，但是需要大量准确的样本进行训练，过度依赖参与训练的数据;电化学方法则是存在计算复杂、效率低、实用性差的问题;粒子滤波算法在面对非线性系统时有着明显的优越性，但是也存在依赖大量数据等缺点。上述的SOC估算算法都各有其优缺点和适用场合。

本文将改进后的拓展卡尔曼滤波算法用于锂电池SOC估算，从最终的实验对比仿真结果可以看出来，改进后的拓展卡尔曼滤波算法对非线性系统的锂电池SOC进行估算具有更好的实时性和更高的精度，弥补了传统安时法因时间长而误差增大的缺点，在面对干扰时也具有更好的估算精度。

1 锂电池等效模型

1.1 PNGV等效电路模型

锂电池等效电路模型是从电池外部特性到内部状态之间的桥梁，能较好的体现电池静态和动态特性，对锂电池的的状态估算、性能分析、科学评价起到基础性的作用[2]。

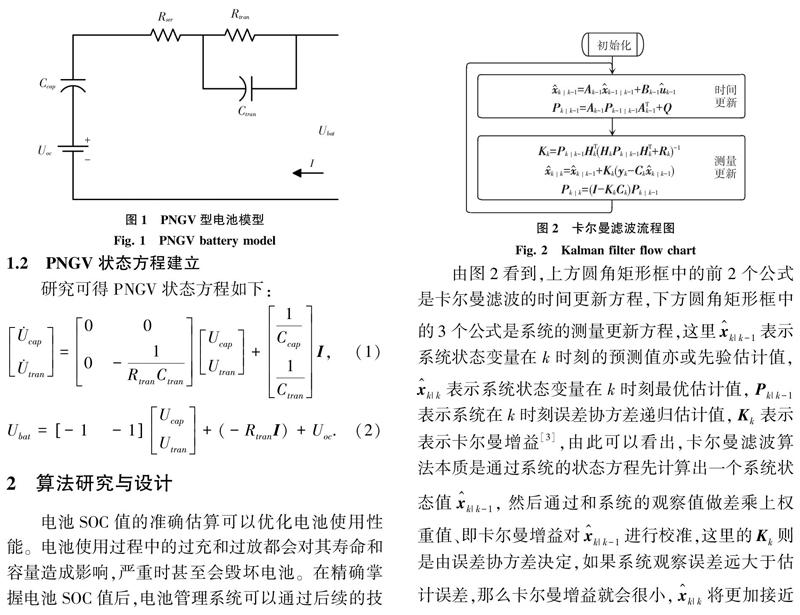
《FreedomCAR功率辅助型混合电动车电池测试手册》中，PNGV等效模型作为电池的代表电路模型，如图1所示。模型中，Ccap为储能大电容，用来描述电池充放电过程中引起的端电压变化，电池充放电引起SOC变化，进而引起电压变化，该电容不仅可以用来准确描述电池的容量，而且也表示直流响应，Rser为欧姆内阻，Rtran和Ctran分别为极化电阻和极化电容，构成的RC电路用来模拟电池内部的电化学极化反应。PNGV模型能够比较完善刻画出电池内部的动态特性，模型中各个参数不仅易于辨识，而且也具有实际的物理意义，因此目前PNGV模型已與各种先进算法相结合，并且广泛应用于电池SOC估算中。

1.2 PNGV状态方程建立

研究可得PNGV状态方程如下：

2 算法研究与设计

电池SOC值的准确估算可以优化电池使用性能。电池使用过程中的过充和过放都会对其寿命和容量造成影响，严重时甚至会毁坏电池。在精确掌握电池SOC值后，电池管理系统可以通过后续的技术手段将电池剩余电量控制在合理的安全范围内，进而避免电池处于过充和过放状态，提高使用效率，延长使用寿命。

利用现如今的技术能够直接检测到的电池参数有电池的充放电电流、端电压、内阻以及电池的环境温度[3]等。

因此如何通过这些检测到的电池电压、电流等参数进行间接的SOC估算即已成为锂电池关键技术研发中一个热点和难点问题。锂电池SOC估算一般都要求能够达到较高的精度、较短的估算时间、以及较强的抗干扰性等设计指标。文中对此拟做研究论述如下。

2.1 卡尔曼滤波

卡尔曼滤波算法本质上是一种递推算法，先根据电池的电路模型转换成对应状态方程，将SOC估算值等作为内部的系统状态，利用前一时刻SOC估算值和目前观测到的电池参数进行SOC参数更新，通过观测值和估算值展开不断迭代，最终得到SOC的最优估计值。这里的观测值容易受到噪声干扰的影响，所以最优估计常被看作是一种滤波过程。卡尔曼滤波设计流程如图2所示。

2.2 基于改进拓展卡尔曼滤波的SOC估算

拓展卡尔曼滤波（EKF）的思想是对非线性系统进行Taylor级数展开，用其一阶量对非线性系统进行近似，然后采用卡尔曼滤波的估计-测量-修正方法来推得后续的SOC估算，相应研究内容详见如下。

EKF是将状态方程和测量函数在状态估计值处用一阶Taylor展开，使模型线性化。其数学公式可表示为：

这里的状态变量是极化电容的电压值和储能电容电压值。

综合前述分析可知，锂电池开路电压和SOC之间存在一定函数关系，一般可以用安时积分法的公式进行表示：

3 实验仿真

3.1 仿真模型建立

为了证实本文锂电池估算算法的准确性，借助Matlab/Simulink工具对本文电池模型和设计算法进行建模并提供动态仿真来验证估算精度。分别利用锂电池充放电数据建立电池模型，仿真模型图如图3所示。同时建立EKF和Ah法估算模型进行对比，而且加入噪声干扰来检验算法的鲁棒性。

对锂电池进行反复充放电，在白噪声影响下的充放电电流和电压曲线如图4、图5所示。反复充放电EKF和Ah法仿真结果如图6所示，而SOC估算误差结果曲线即如图7所示。

3.2 实验结果分析

从图4、图5可以看出，当对电池进行反复充放电时，不同的算法对锂电池SOC估算结果存在巨大差异。从图6可以看到，在充放电期间，随着充放次数的增加，在外部噪声的干扰下，EKF和安时法对SOC估算结果呈现出明显差异。随着充放电时间的增加，最终也绘制得到并不相同的SOC结果曲线。其中，安时法在后续锂电池静置状态下对SOC的估算超过了100%，这是由于前期噪声的干扰所导致的。由于Ah法没有引入实时观测值进行修正，在估算精度上与EKF法仍有差距，而EKF算法成功引入了观测量，能够对估算过程中的误差进行实時修正，如此一来就减小了因噪声等干扰造成的累计误差，因而也得到了更好的实时性和准确性。

由图7也可以看出，本文的EKF算法在噪声干扰下对锂电池SOC估算比传统Ah法具有高的精度和更好的鲁棒性。

4 结束语

本文对锂电池传统和新型SOC估算算法进行了研究分析。在传统卡尔曼滤波算法的基础上，将其改进变换成拓展卡尔曼滤波算法（EKF）后，同锂电池PNGV电路模型相结合对锂电池进行SOC估算。

本文最后还将SOC联合估算算法与传统方法加以综合比较，通过Matlab/Simulink中建立电池的综合仿真模型对SOC算法实现了仿真与评估，同时验证了其准确性，进而证明了本文算法比传统的SOC估算算法面对噪声干扰时具有更好的鲁棒性和准确性。

参考文献

[1]陈玺. 电动汽车用电池管理系统设计[D]. 北京：华北电力大学（北京）， 2016.

[2]郑敏信， 齐铂金， 吴红杰. 锂离子动力电池组充放电动态特性建模[J]. 电池， 2008， 38（3）：149-151.

[3]ZHANG Zhiliang， CHENG Xiang， ZHOU Yulu， et al. SOC estimation of lithium-ion batteries with AEKF and Wavelet transform matrix[J]. IEEE Transactions on Power Electronics， 2016（99）：1.

[4]欧阳佳佳.  储能电池管理系统研究[D]. 杭州：浙江大学， 2016.

[5]周胜. 基于双卡尔曼滤波算法的磷酸铁锂电池建模及SOC估计[D]. 成都：西南交通大学，2017.

[6]甘屹， 李杨， 姚俊. 基于PNGV模型储能锂电池参数辨识及SOC估算研究[J]. 能源研究与信息， 2017，33（4）：194-199.

[7]KUMAR B， KHARE N， CHATURVEDI P K. FPGA-based design of advanced BMS implementing SoC/SoH estimators[J]. Microelectronics Reliability， 2018， 84：66-74.

[8]李争， 高越， 王群京. 基于Simscape的动力锂离子电池的建模与仿真[J]. 电源技术， 2017，41（11）：1533-1536.

[9]赵天意， 彭喜元，彭宇，等. 改进卡尔曼滤波的融合型锂离子电池SOC估计方法[J]. 仪器仪表学报， 2016， 37（7）：1441-1448.

[10]LI Xiaoyu ， FAN Guodong， RIZZONI G ， et al. A simplified multi-particle model for lithium ion batteries via a predictor-corrector strategy and quasi-linearization[J]. Energy， 2016， 116（1）：154-169.