新型多目标遗传算法在烧结配矿中的应用
王策 董兆伟 孙立辉 姜军强

摘 要:在烧结配矿过程当中,往往需要对产品质量、原料成本等多个目标同时进行寻优处理。面对这种约束条件复杂,变量较多,各目标分布情况复杂的多目标优化问题,本文提出了一种新型多目标遗传算法对其进行解决。通过改进算法中的非劣排序步骤,过滤种群中产生的不合理个体,并添加去重操作,降低种群中个体的重复出现,增强种群中个体的多样性。该算法能够为钢厂的烧结配矿工作提供较为合理且成本、质量都较为优秀的配矿方案。
关键词: 烧结;遗传算法;配矿;多目标
文章编号: 2095-2163(2019)03-0036-05 中图分类号: TP301.6 文献标志码: A
0 引 言
当前的烧结配矿优化模型,大多是以成本最优为目标的单目标优化模型,得到的结果只能反映成本问题,但是烧结矿中的质量问题却无法呈现,其中以烧结矿中硫含量、碱金属等有害物质的含量问题最为突出,钢铁企业在降低生产成本的同时更加希望对有害物质含量进行最优化处理。
作为一个多目标寻优问题最大的难点在于优化的多个子目标难以同时达到最优的状态,往往是一个子目标结果优秀而其他子目标的性能结果降低,所以为了得到满足实际生产所需的最佳配矿方案,只能在搜索范围内的所有较为优秀的方案中对一些目标要求进行降低,采取一种折中的态度选择优秀方案中的最符合要求且子目标冲突可以接受的方案[1]。本文以每吨原料成本最低和烧结矿中硫含量最低作为寻优目标,建立双目标烧结配矿优化模型,通过数据实验解析当前问题中的难点,并对经典的多目标遗传算法(NSGA-Ⅱ)进行改进,寻找对钢厂实际生产具有指导意义的配矿方案。
1 模型建立
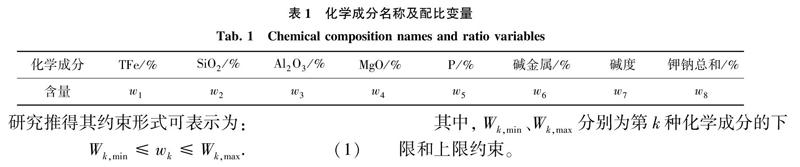
在烧结配矿模型建设当中,约束条件保证了烧结矿的质量性能,因此过程中涉及的几种化学成分和其含量符号见表1。
研究推得其约束形式可表示为:
为了降低约束条件对计算速度的影响,采用惩罚函数形式处理化学成分和原料配比组成约束条件[2],具体处理方式可参考如下运算公式:
其中,xj为第j种原料的配比变量,W、P为约束惩罚项,为q个非线性约束条件和等式约束条件的惩罚项表达形式,每当违反约束条件后则增大约束惩罚项的值。
多目标适应度函数的定义表示如下:
其中,f1为n种原料配矿的方案成本和惩罚项共同组成的适应度函数;cost为原料的吨成本;α、β为惩罚项阈值;f2为烧结矿中的硫含量。
这2个目标适应度共同组成多目标烧结配矿优化系统的寻优目标。
2 算法设计
在寻优过程中控制整体的搜索范围和搜索趋势,将运用选择机制与快速非劣性分层方法结合的方式降低计算量。然后面对试验当中出现的问题调整算法改进的主要研究方向,再重点根据出现的问题对算法步骤做出改进,研究内容分述如下。
2.1 快速非支配分层排序改进
NSGA-Ⅱ算法通常采取精英保留策略,将交叉变异后的新种群与旧种群结合为一个种群,组合种群经过非支配层排序后进行选择操作,但是进行非支配层排序时会用到大量的计算,严重耗损计算时间[3]。基于此,本文就去除NSGA-Ⅱ算法中选择操作,将其融入到非支配层排序操作中,与此同时在非支配排序过程中即可判断、并确定被选择出的个体数,若满足种群数时将停止非支配排序,使计算量得以减少。
通过对钢厂的多组实际生产数据试验发现,在随机生成的遗传种群中具有优秀成本的方案变量都聚集到了定义域中的一个极小的范围内,详见表2。表2中的数据则为实际生产数据进行试验时的第一层非支配层中的部分数据。
通过试验数据可以看到,有些个体虽然硫含量极低,但是成本很高,根本无法满足成本与硫含量最优的寻优目标,而且考虑到NSGA-Ⅱ算法的寻优过程都是通过精英保留策略进行个体选择,所以就可能使得那些无法满足目标的个体被保留、甚至被复制,此后又经过交叉操作,将会产生更多的无用个体占据种群位置,而满足寻优目标的个体数量会被压制,整个算法的搜索效率和范围将会受到影响,无法获得满足要求的Pareto解集。
综合前述分析,本文将当前得到的非支配层中的个体分别按照2个目标进行从小到大分类,选取该层所有个体中的2个目标函数的最小值,即f1,min、f2,min,对这2个最小值进行如下变换,可得数学公式为:
其中,h1、h2为大于1的2个权值,l1、l2为大于0,小于1的权值,且h1-l1、h2-l2都大于1;i为当前遗传运行代数;Maxgen为遗传算法最大代数。
当计算得到2个值L1、L2后,将所有个体的目标适应度与L1、L2加以比较,一旦个体中的2个目标适应度大于这2个数值,该个体将被剔除。分析可知,这一方法可以去除种群中的特殊个体,保留符合要求的个体。并且随着非支配层层数的增加来对每一层进行过滤。
接下来,研究中给出改进后的快速非支配排序的算法流程可表述如下。
Step 1 对随机生成的初始种群S1进行排序,寻找到种群中所有不被任何其他个体支配的个体I,在种群S1中个体I可能不止一个,定义这些个体I的序号为0,将这些个体组成集合F1,F1中的所有个体就组成第一非支配层。选取各个目标在该层中的最小值,根据公式(3)来计算多目标值上限,再对该层中個体进行过滤,只保留符合要求的个体。而后则判断该支配层中的个体数是否大于等于种群数n。如果是,该层个体将进行拥挤度计算,选择拥挤度排序前n位的个体作为选择种群,进行遗传操作。如果否,则转入Step2。
Step 2 剔除种群S1中所有不被任何其他个体支配的个体,也就是剔除所有属于集合F1中的个体,将种群S1中剩余的个体组成种群S2,并在种群S2中寻找不被任何其他个体支配的个体,同时将这些个体序号定义为1,将这些不被其他个体支配的个体组成集合F2,对集合F2中的所有个体根据各个目标依次排序,选取各个目标在该层中的最小值,根据公式(3)进行计算,据此对该层中个体进行过滤,过滤后集合F2中的所有个体成为第二非支配层。判断已被分配的非支配层中的个体总数是否大于等于种群数n。如果是,将最后一层个体进行拥挤度计算,选择最后一层中拥挤度排序靠前的个体与除去最后一层的所有非支配层中的所有个体作为选择种群,然后启用遗传操作。如果否,则重复Step2,直到满足种群数量的所有个体都被分层为止。
Step 3 当所有个体都经过Step1、Step2的个体过滤操作后,保留的非支配层个体数量无法满足种群数量,则随机在已保留的非支配层中选择个体进行复制,再保存到非支配层中,直到非支配层中的个体数量满足种群数量为止。
2.2 去重操作
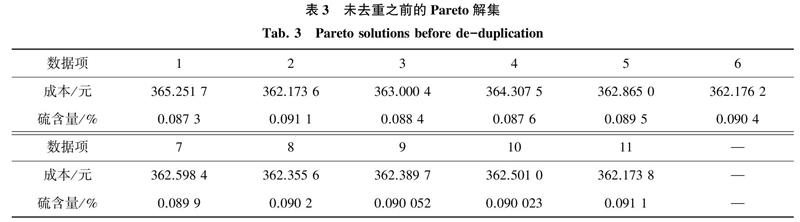
由于使用了精英保留策略,大量的优秀个体会被保存重复出现在种群中,这将直接影响算法的全局搜索性能,并将种群中的大量个体都变为重复个体。由于交叉变异操作的随机选择,还会有很多重复个体无法变异而得以保留,进行变异的个体也有很大可能会处在重复个体的变量周边范围内,造成遗传算法的早熟现象,产生的最佳Pareto解集相似度极高[4-5],此时的运行结果详见表3。难以满足求得的多组相对优秀方案需各具差异性的要求,无法为使用者提供足够的选择,同时也无法体现算法搜索的优越性,在变量的定义域内可以搜索到更加优秀的方案。
为了解决这一问题,本项目组在将父代、子代种群彼此混合后,即对混合种群中的个体展开判断,当个体重复个数大于某个整数值Z时,删除多于整数值的所有重复个体。为了在种群进化的后期增强种群中个体的多样性,在算法每次执行一定代数后缓慢降低种群内被允许的个体重复个数Z,在种群进化的最后一代时,保证种群中个体重复个数Z不为1,使种群中存在一定的重复个体,此后再将经过去重操作处理后的混合种群进行快速非支配分层排序。
2.3 遗传操作
本文将某钢厂的实际生产数据作为试验应用数据,在算法寻优过程中可根据遗传算法将种群中个体的基因变量随机分布到整个变量定义域,再进行搜索范围收缩的特点,经过大量实验,发现了种群中优秀方案的2个目标适应度和个体基因变量处于定义域内的分布规律,即优秀成本目标值分布较为集中、而优秀硫含量目标值分布较为均匀,为了能得到成本和硫含量双目标都较为优秀的个体,本次研究即在交叉操作中采用基因位直接交换的方式,变异操作所采用的自适应变异方式的数学方法可写作如下形式:
改进后的NSGA-Ⅱ算法运行步骤如图1所示。
3 实验结果分析
经过多组钢厂的实际生产数据对该改进型算法进行验证,该算法可以在用户初始设置的原料配比和烧结矿质量指标的约束条件下,搜索到既能降低每吨原料成本,也能降低烧结矿中硫含量的多组配矿方案供用户根据自身需要来挑选合适的配矿方案,研究时参见表4。其中,以方案名为“三铁烧结3.2原配比”中的配比原料信息作为算法中个体变量信息进行输入,对质量指标进行约束处理得到了一组优秀配矿方案和以成本最优为单目标的经典遗传算法寻优方案、以及原厂数据方案进行对比,可以看到效果较为明显。
同时,为了比较各个方案的差异性,研究中选择将多目标算法模型计算出的解集方案中的1、4、8、12号方案与以成本最优为单目标的经典遗传算法寻优方案,以及钢厂的“原数据三铁烧结3.2原配比”方案进行对比,结果见表5。
由表4、表5中数据的对比情况分析可知,该改进的NSGA-Ⅱ算法可以在满足用户所需要的质量指标的约束前提下,寻找到多组能够为用户使用的合理方案,解决了经典NSGA-Ⅱ算法在研究该问题中出现的一些问题。
4 结束语
NSGA-Ⅱ算法是一種优秀的多目标寻优算法,但是由于烧结矿成本和硫含量这2个目标值在个体定义域中分布不均匀的原因将无法搜索到优秀的Pareto解集。基于这一问题状况,本次研究对经典NSGA-Ⅱ算法进行改进,通过增添去重操作,缓解由精英保留策略导致的个体重复率太高的不足,增强种群个体的多样性,通过在快速非支配层排序中增添极值过滤的操作,降低极端目标值个体对序号靠前的非支配层个体的影响,并且将截断式的个体选择方式融入到快速非支配层排序当中,优化缩简了计算量和计算时间,增强了Pareto解集在实际生产操作中的合理性和指导性。通过前文研究中的数据对比结果可知,该算法可以明显改善配料方法,降低原料成本和烧结矿中的硫含量,增强烧结矿的质量性能,减少钢铁的热脆现象,为钢铁企业带来可观的经济效益,提高钢铁的生产质量。
参考文献
[1]肖晓伟, 肖迪, 林锦国,等. 多目标优化问题的研究概述[J]. 计算机应用研究, 2011, 28(3):805-808,827.
[2]陈婕, 熊盛武, 林婉如. NSGA-Ⅱ算法的改进策略研究[J]. 计算机工程与应用, 2011, 47(19):42-45.
[3]邓富民, 梁学栋, 刘爱军,等. 多资源约束下改进NSGA-Ⅱ算法的手术调度[J]. 系统工程理论与实践, 2012, 32(6):1337-1345.
[4]王广博, 韩庆, 钟小平. NSGA-II中重复个体的控制[J]. 科学技术与工程, 2011, 11(34):8602-8604,8623.
[5]谢炯亮, 郑金华. NSGA-Ⅱ中重复个体产生原因分析及影响研究[J]. 计算机工程与应用, 2008, 44(29):69-72,145.

