基于Matlab的细纱机集落升降系统力学及位移分析

徐兆山，唐国新，毛阿平

(常州市同和纺织机械制造有限公司，江苏 常州 213000)

0 引言

细纱是纺纱过程中至关重要的一道工序，它对纱线质量、产量及整个工厂的运转都有极其重要的影响。随着棉纺技术的进步及纺纱设备自动化程度的提高，细纱机集落系统可实现筒管的自动插管和满纱管的自动落纱，使其成为棉纺企业提高生产效率、降低用工成本的一个重要环节。因此，环锭细纱机配备集体落纱系统，已成为目前棉纺企业的选择趋势。

Matlab是一款集强大的数值计算、符号运算、建模仿真、图形处理及可视化等多功能于一体的科学计算软件，在科学研究和产品开发领域有重要作用。笔者通过该软件得到精确的细纱机集落升降各位置的坐标值，并绘制出细纱机集落升降力学及位移特性曲线，解决了手工设计时计算繁琐的问题，为细纱机集落升降驱动电机选型及机械调试[1]提供理论依据，从而有效地提高了设计速度和制造效率。

1 细纱机集落升降系统运动模型的建立

1.1 集落升降系统的连接及运动规律

细纱机集落升降系统结构，如图1所示。其中，集落升降系统的支撑长臂铰接固定在传动轴上，支撑短臂铰接固定在细纱机墙板上，支撑短臂与支撑长臂之间铰接固定，且支撑长臂的长度是支撑短臂的2倍。伺服电机通过减速箱、滚珠丝杠副通过2个丝杠副支撑座均固定在细纱机底板上，丝杠螺母与传动轴连接固定，伺服电机通过减速箱及齿形带/链条驱动滚珠丝杠副旋转运动，传动轴通过滚珠丝杠副的旋转运动进行水平直线往复移动，当传动轴移动时，握纱横梁进行垂直上升或下降运动。

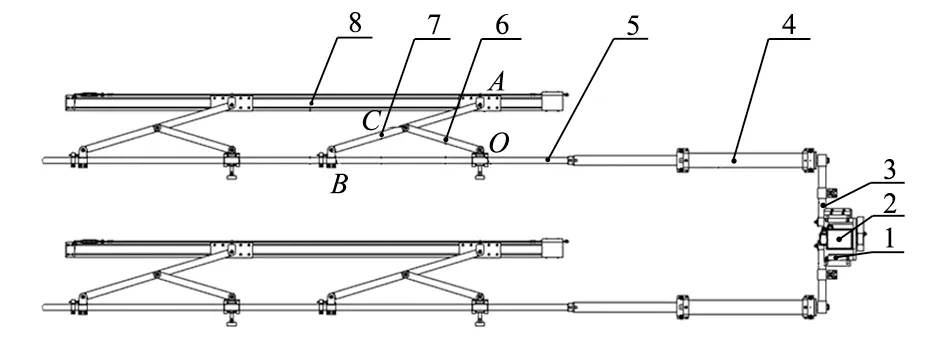
1—减速箱；2—伺服电机；3—齿形带/链条；4—滚珠丝杠副；5—传动轴；6—支撑短臂；7—支撑长臂；8—握纱横梁。图1 集落升降系统结构示意

1.2 人字臂结构力学及位移分析

人字臂结构如图2所示，其中，AC=CB=CO，O点固定，AB、OC通过铰链连接，当点B沿BO方向移动，α+β=γ+θ=90°且β=γ时，点A始终在垂直于BO的垂线AO上作上下移动。

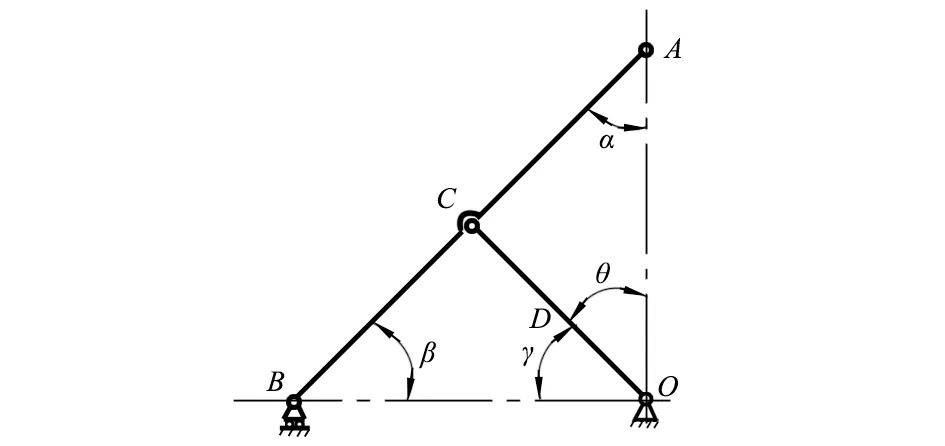
图2 人字臂结构示意

在实际机构中，机台两侧的握纱横梁由多组人字臂支撑，各支撑长臂的下支点通过铰链座与传动轴连接，并由丝杠副驱动。为研究方便，假设单侧握纱横梁的总质量施加在一组人字臂结构上，并视人字臂、握纱横梁、传动轴为刚体，忽略其弹性变形，且不计各铰链处的摩擦力，这样就形成理想约束状态下的坐标系平衡模型，如图3所示。图中，D为支撑短臂质心，亦是中点；γ为BO与CO的夹角，即支撑短臂与传动轴之间的夹角；G0为单侧握纱横梁及其它零部件的总质量(含横梁连接座、握纱器和纱管等)；G1为单侧支撑长臂总质量；G2为单侧支撑短臂总质量；FxB为维持系统的平衡力。

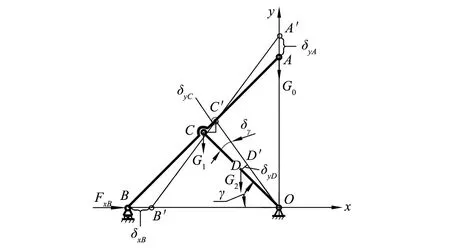
图3 人字臂力学及位移坐标系平衡模型示意

根据理论力学中的虚位移原理[2]，推导坐标系中γ与维持系统平衡的拉力FxB之间的关系。当γ确定时，该系统的位置就确定了，所以该系统属于单自由度系统，γ为广义坐标，作用于该系统上的G0，G1，G2，FxB就是主动力，那么该系统上任何一点的虚位移均可通过广义坐标的增量δγ来表示。

设CO=AC=BC=L，则点A，B，C，D的虚位移分别为δyA，δxB，δyC，δyD，则：

C点处y轴坐标为：yC=L×sinγ

变分为：δyC=L×cosγ×δγ

同理，δyD=1/2×L×cosγ×δγ

又因点B与原点O的距离：BO=2×L×cosγ

变分为：δxB=-2×L×sinγ×δγ(负号表示当δγ增大时，δxB减小)

另因点A与原点O的距离：AO=2×L×sinγ

变分为：δyA=2×L×cosγ×δγ

根据虚位移原理，所有作用于系统上的主动力在任何虚位移中所作虚功的和为零：

即δW=FxBδxB+G0δyA+G1δyC+G2δyD=0，则：

FxB×2L×sinγ×δγ=G0×2L×cosγ×δγ+G1×L×cosγ×δγ+G2×1/2×L×cosγ×δγ，得：

FxB=cotγ(G0+G1/2+G2/4)

(1)

式(1)中，γ是决定FxB最主要的因素。当0°<γ<90°时，G0，G1，G2是升降系统各零部件的自重，为常数。令a=G0+G1/2+G2/4，将a视为单位，则式(1)可简化为：

FxB=cotγ

(2)

根据勾股定理得：

yA2+xB2=4L2

(3)

2 Matlab程序设计及特性曲线绘制与分析

2.1 Matlab程序设计

以同和公司的TH598系列自动落纱细纱机为例，编制程序并绘制特性曲线[3]。其中：CO=AC=BC=L=525 mm，则当AB=1050 mm时，AB2=BO2+AO2，15°<γ<72°，BO=AB×cosγ。

2.1.1根据式(1)在Matlab编辑器中编写的M文件程序如下。

% 采用符号函数

%1)fpolt

subplot(1,2,1)

FxB=inline(′cot(gamma)′)；

% 定义函数

a=pi/12；

b=2*pi/5；

% 定义横轴区间

fplot(FxB,[a,b])；

% 符号函数绘图

grid on；

% 网格线

% 标注图形名称和坐标轴名称

title(′TH598系列自动落纱细纱机集落升降力学特性曲

线′)

x1=[pi/12 2*pi/5]；

x2=[0 0]；

line(x1,x2)；

% 绘制横轴

xlabel(′pi/12leq gamma leq 2*pi/5′)

% 标注x轴

% 标注y轴

% 标注曲线函数式

%2)ezpolt

subplot(1,2,2)

a=pi/12；

b=2*pi/5；

gamma=a∶pi/50∶b；

FxB=inline(′cot(acos(-xB/1050))′)；

% 定义函数

ezplot(FxB,[-1050*cos(a),-1050*cos(b)])；

% 符号函数绘图

grid on；

% 网格线

% 标注图形名称和坐标轴名称

title(′TH598系列自动落纱细纱机集落升降力学特性曲

线′)

x1=[a b]；

x2=[0 0]；

xlabel(′-1015leq xBleq -300′)

% 标注x轴

% 标注y轴

% 标注曲线函数式

2.1.2根据式(3)，在Matlab编辑器中编写的M文件程序如下。

% 绘制二维曲线

xB=-1015∶1∶-300；

yA=(1050.^2-xB.^2).^(1/2)；

plot(xB,yA)；

grid on；

% 网格线

% 标注图形名称和坐标轴名称

title(′TH598系列自动落纱细纱机集落升降位移特性曲

线′)

xlabel(′xB′)

ylabel(′yA′)

% 标注曲线函数式

text(-900,900,′yA=(1050.^2-xB.^2).^(1/2)′)

2.2 绘制特性曲线

2.2.1 绘制细纱机集落升降力学特性曲线

在Matlab环境下，运行程序生成特性曲线[4]，如图4所示。

图4 细纱机集落升降力学特性曲线

运用Matlab图形窗口下工具栏中的数据游标按钮，即可读取特征曲线中任意点数值，见图5。

2.2.2 绘制细纱机集落升降位移特性曲线

在Matlab环境下，M文件程序生成特性曲线，如图6所示。

运用Matlab图形窗口下工具栏中数据游标按钮，即可读取特征曲线中任意点数值，如图7所示。

2.3 特性曲线分析

分析上述特性曲线，可得以下结果。

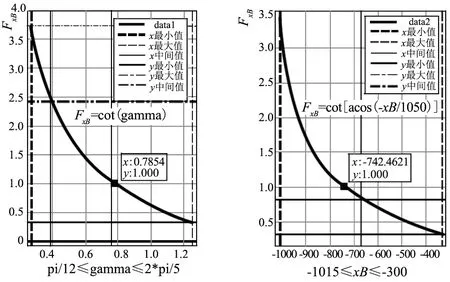
图5 细纱机集落升降任意点力学特性曲线

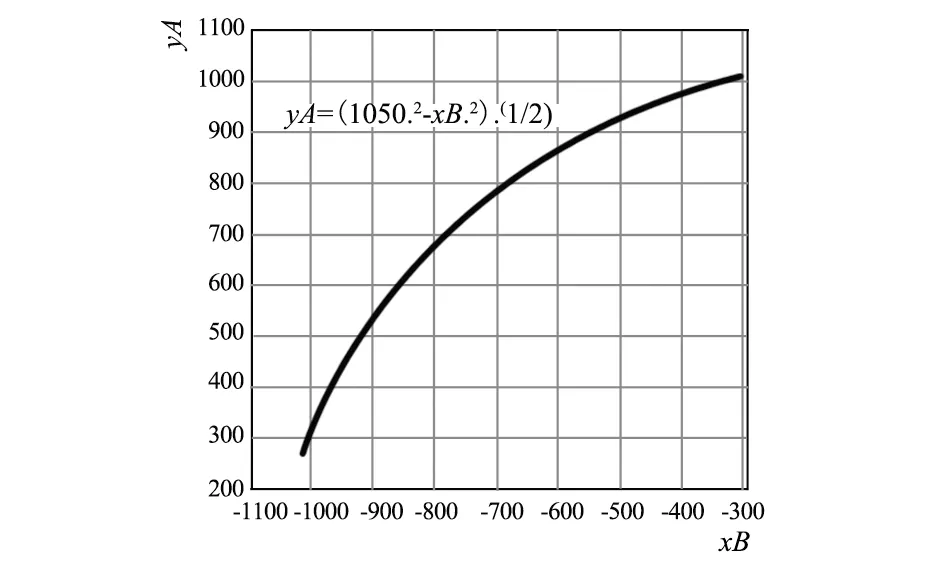
图6 细纱机集落升降位移特性曲线

图7 细纱机集落升降任意点位移特性曲线

a) 当γ增大时cotγ减小，则FxB随γ增大而减小；当γ为最小值(传动轴BO两点距离最长)时，在最低位抓空管即将启动时FxB将达到最大值。此外，当γ=45°(传动轴BO等于握纱横梁高度AO，即两点距离为742.462 1 mm)时FxB=a；当γ<45°时FxB>a；当γ>45°时FxB

b) 当xB增大(BO减小)、yA增大(AO增大)，且成抛物线比例关系，即BOxB增幅；BO>AO时(即γ>45°)，yA增幅

通过上述分析及式(1)和式(3)可得：

a)γ和集落升降系统各零部件的自重是决定FxB的主要因素；支撑长臂总质量G1和短举升臂总质量G2对FxB的影响较G0小；在系统处于最低位时，3.732a是维持系统平衡力很大的数值。因此，在设计中需增设助推辅助装置，降低系统功耗，提高机械效率。另外，FxB只是单侧维持系统平衡的力，其来自集落升降系统的驱动力与传动轴受到的摩擦力的矢量和，同时传动轴受到的摩擦力的方向在握纱横梁的下降和上升过程中亦是变化的，在驱动电机选型过程中更是不容忽视。

b) 在人字臂上升过程中，传动轴两点距离为742.462 1 mm时(γ=45°)，其与握纱横梁的高度增幅比是个转折点。因此，在集落升降机械调试确定各点位置时，切记注意机械调节量，避免撞车。

3 结语

Matlab软件与机械原理和机械设计结合，充分运用其处理数据和图形显示的功能，不仅实现了产品的可视化设计和精确计算，而且有效提高了设计质量，缩短了设计周期；这种方法亦对其他机械产品的设计提供了有益参考。