轨道交通线网拓扑结构模型及节点重要度分析

谌微微，张富贵，赵晓波

(1. 重庆交通大学 经济与管理学院，重庆 400074； 2. 重庆市轨道交通设计研究院有限责任公司，重庆 401122)

0 引 言

轨道交通网络的建设日趋复杂，线路、站点数量越来越多，在运行中出现故障的情况也时有发生。如重庆市轨道3号线因故障导致12个站点停摆达8个多小时；北京市地铁4号线角门西站早高峰时发生故障，大量旅客滞留，严重影响了整个网络的正常运行。针对上述问题，学者们对轨道交通网络运营安全[1]、可靠性[2]、可达性[3]、网络性能[4]等开展了研究。然而，轨道交通网络作为一个巨系统，从全局角度分析其结构更有利于发现关键节点、制定资源配置方案和应急事故处理方案。因此，对轨道交通网络的拓扑结构及节点重要度分析具有重要价值。

轨道交通网络已被众多学者证明属于一种典型的复杂网络系统。研究表明，轨道交通网络具有显著的小世界性和无标度性[5-6]。因而，复杂网络也成为对轨道交通网络进行研究的重要方法。A. L. BARBASI等利用复杂网络理论构建城市轨道交通路网的复杂网络拓扑结构[7]。在此基础上，S. DERRIBLE分析了由全球28个城市的地铁系统换乘车站和终点车站构成的复杂网络的网络介数[8]；高天智等则选取中国10个典型城市的轨道交通网络的宏观特性进行了研究[9]。进一步，马嘉琪等从宏观和微观两个角度对北京市轨道交通网络性能进行了综合分析[10]；而孟天奇等以北京、上海的轨道交通网络为对象，从网络基本特征、空间分布、网络结构等指标入手进行对比[11]。除此以外，轨道与公交换乘网络亦是学者们的研究对象。如赵淑芝等利用复杂网络优化后交通网络可使换乘时间缩短16%，系统总费用节约6.16%[12]。轨道交通的重要功能为载客。因此，陈培文等以车站为研究对象，构建网络分流模型，提出城市轨道交通网络的客流中心性指标，进一步识别出北京地铁的重点车站[13]；秦孝敏试图探寻平稳运行中的脆弱节点[14]；而程光权等基于节点的动态演化模型提出节点重要度评估和网络结构脆弱性分析方法[15]。以此为基础，杜斐等[16]、刘志谦等[17]分别构建了上海、广州轨道交通的网络拓扑结构，并对网络中站点遭遇随机故障和蓄意攻击情况下的鲁棒性进行研究。在以往研究中，北京、上海、广州、武汉等重要城市的轨道交通网络均为学者的重要研究对象，而作为直辖市之一的重庆，轨道交通发展相对滞后，对其网络结构特性的研究较为缺乏，难以对其实际运维工作进行有效指导。鉴于此，笔者综合采用二阶张量及复杂网络方法构建轨道交通线网拓扑模型，对模型的度和度分布、网络直径、平均路径长度、聚类系数等网络整体特征指标进行分析，并用3个中心性指标评价其网络节点重要度，以指导相关部门制定轨道交通网络资源配置方案和应急事故处理方案，同时对轨道运营公司日常防护工作及网络结构优化提供有效参考。

1 复杂网络基本理论

网络存在于人们生活的各个方面，如交通运输网、互联网、科研合作网、供电网、社交网、城市网、港口网等。轨道交通网络是由区间线路将各个车站连接在一起的典型复杂网络系统，可抽象为由站点集V和区间线路集E组成的图G=(V,E)。其中，站点数用N=|V|表示，区间线路数用M=|E|表示。E中任意一条区间线路都有V中一对站点与之对应。若任意的一对站点(i,j)与(j,i)对应于同一条区间线路，则该网络成为无向网络。

1.1 度与度分布

(1)

假定在轨道交通网络中有N个站点，站点i的度ki表示任意站点与其他直接相连的站点数量，则对于站点i的度：

(2)

所有节点度的平均值为该网络的平均度，用表示。在轨道交通网络中，平均度表示该网络中一个站点与其他站点直接相连的平均站点数量：

(3)

无标度网络节点的累积度分布P(k)呈现幂律分布，即：

(4)

式中：p(i)为站点度为i的站点占总节点数的比例；kmax为网络中站点度的最大值；γ为幂率指数。

为了更好地验证轨道交通网络是否为无标度网络，可以通过分析其网络的节点度分布特征，然后对节点累积度分布进行曲线拟合。

1.2 网络直径与平均路径长度

网络中任意两节点间的距离称为连接该两节点的最短路径的边数，其中距离的最大值定义为该网络的直径[20]。在轨道交通网络中，任意两个站点i、j间的距离dij为连接这两个站点的区间线路数，其中最大值为该轨道交通网络的网络直径D，即：

(5)

两个任意站点间的距离的平均值定义为网络的平均路径长度L，即：

(6)

在轨道交通网络中，平均路径长度表示该网络中平均最短路程需要经过的区间线路数，在一定程度上反映了网络的规模大小。

1.3 聚类系数

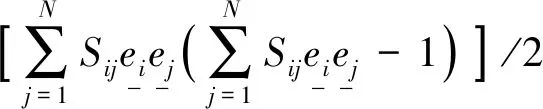
在轨道交通网络中，聚类系数表示网络中直接相连的站点比例，在一定程度上反映该网络的复杂程度。

2 轨道交通网络模型及特性

2.1 轨道交通复杂网络拓扑结构模型

轨道交通网络拓扑结构是理解其性质和功能的基础。该网络是由车站和车站之间的线路连接而成的交通运输网，其基于Space L法[21]建立网络拓扑结构，即以车站为节点、车站之间的线路为边、相邻车站间距离为边的长度来构建拓扑结构的方法，并作如下假设：

1)将站点抽象为质点，通过质点间的联结关系建立网络拓扑结构，故现实站点及其距离在该拓扑结构中对整体性能和实际运行中站点重要度分析的影响可忽略。因此假设所有相邻且有直接相连的车站间长度相等，长度假定为1。

2)轨道交通网络具有双向通行的特点，即同一站点的出度和入度大致相等，因此可以将其抽象为无向网络。

3)一个车站为一个节点，换成车站看作是与多个节点相连单个节点，车站用υi表示。

4)重点考虑轨道线网拓扑特性及拓扑结构中的节点重要度，忽略实际运行中的客流变化、车辆编组、发车时间等因素，将其简化为非计权网络。

基于前述假设，构建轨道交通复杂网络拓扑结构模型，如图1。

图1 轨道交通复杂网络拓扑结构模型Fig. 1 Topological structure model of rail transit complex network

2.2 轨道交通网络特征描述

用Space L法构建的复杂网络，其典型的网络特征描述指标包括网络节点数、边数、平均度、平均路径长度、网络直径、平均聚类系数等。这些指标从不同角度反映网络的特征，综合起来考虑能够比较全面反映整个网络的特征。

用Gephi 9.1建立轨道交通网络拓扑结构，进一步可以分析得出该复杂网络的特征描述指标。

2.3 轨道交通网络节点重要度指标

判断整个网络中任意一个节点的重要程度的首要因素为该节点在网络中所处的位置。位置越中心的节点，其重要程度越高[22,23]。在对复杂网络进行分析时，通常用“中心性”来表示节点在网络中所处的位置。进一步，对轨道交通网络中节点重要度评价主要通过分析拓扑图中各节点所处的位置，并刻画其“中心性”的数组对其所处位置进行排序，以此反映出不同的重要程度。“中心性”数据主要分为3类，分别反映网络中节点所起的不同作用。

2.3.1 点度中心性

点度中心性表征特定节点直接与其他节点有连接关系的节点数量，是刻画节点中心性最直接的度量指标[24]。一个节点的点度中心性越高意味着该节点在网络中越重要。

在轨道交通网络中，点度中心性测量该网络中特定站点与其他所有其他站点相连接的程度。若该网络共有g个站点，站点i与其他g-1个站点的直接连接总数可用二阶张量进行计算：

(7)

2.3.2 接近中心性

接近中心性描述特定节点与其他所有节点的平均最短距离值[24]，反映特定节点与其他节点的接近程度。

在轨道交通网络中，接近中心性是指特定站点与其他所有站点的平均最短距离，表征了该站点在整个网络中所处的位置。若用CC(i)表示站点i的接近中心性，则：

(8)

2.3.3 中介中心性

中介中心性以经过特定节点的最短路径数目来反映该节点在整个网络中的重要程度[20]，可以度量节点在网络中对其他节点或资源信息的控制能力。

在轨道交通网络中，中介中心性表示在寻找网络最短路径时经过特定站点的次数，反映了该站点的资源控制能力。若用CB(i)表示站点i的中介中心性，则：

(9)

3 重庆市轨道交通网络的实证分析

重庆市轨道交通是服务于重庆大都市的、以地铁系统和跨座式单轨系统共存的城市轨道交通系统。截止2016年12月31日，重庆轨道交通总运营里程达213.19 km，全国排名第六；2050年远景规划的“十七线一环”共18条线路运营总里程将达到820 km，约占我国城市轨道规划建设总里程的6.3%。

3.1 重庆市轨道交通网络拓扑结构分析

依据“十七线一环”重庆市轨道交通远期规划绘制网络拓扑图，如图2。图2中：节点代表车站；连线代表两个站点之间的线路；每条边上的权重均为1；有多条边通过的节点代表换成车站。

网络统计特征指标结果见表1。由表1可知：重庆市轨道交通网络拓扑结构中节点数为354，边数为434，表示该网络中运营站点共354个，区间线路共434条；平均度为2.433表示在该网络中平均一个站点与2.433个其他站点直接相连；平均路径长度为13.986表示该网络中平均最短路程要经过13.986个站点；网络直径为40表示该网络中最长的一条线路要经过40条区间线路；聚类系数为0.007，相比于目前已经开通和在建的轨道交通网络聚类系数有大幅提升[17],说明新的线路的运营可使部分站点由不直接相连变成直接相连。

图2 重庆市轨道交通网络拓扑模型Fig. 2 Topology model of Chongqing rail transit network

特征指标数值特征指标数值节点数354平均路径长度13.986边数434网络直径40平均度2.433平均聚类系数0.007

对重庆轨道交通网络中节点度分布p(x)和累积度分布P(k)进行统计分析，度数为1的节点为某线路的起点站或终点站，度数为2的节点为只有一条线路通过该站点，度数大于2的节点为换乘站，如图3、图4。由图3可知：重庆轨道交通网络中度数为2的站点占总数的70.5%，即该网络中有265个站点仅有一条线路通过；度数大于2的站点占总数的25%，即该网络中共有89个换乘站点，换成站点的数量若进一步增加，将更有利于网络顺畅运行。

图4 的拟合曲线中，R2表示拟合程度的好坏，R2越趋于1越好。由图4可知，重庆市轨道交通复杂网络具有显著的小世界性和无标度性。

图3 重庆市轨道交通网络节点的度分布Fig. 3 Node degree distribution of Chongqing rail transit network

图4 重庆市轨道交通网络对数坐标累积度分布拟合曲线Fig. 4 Logarithmic coordinate cumulative distribution fitting curve of Chongqing rail transit network

3.2 重庆市轨道交通网络节点重要度分析

根据基本假设建立关于重庆市轨道交通网络模型，该模型为包含354×354个元素的二阶张量，以此进一步对其复杂网络特性进行分析，如图5。

由图5可知，节点与连线只代表联结关系，不代表具体节点位置和实际距离。天生、北碚等节点仅有一条线路通过且未能形成闭环，冉家坝、五里店等节点与其他节点和线路形成了环路；节点大小与该节点与其他节点直接连接的个数成正比。通过对网络各节点的中心性指标进行分析，评价各节点对于整个网络的重要程度。

图5 重庆市轨道交通网络线网拓扑图Fig. 5 Topology diagram of Chongqing rail transit network

通过对网络各节点的中心性指标进行分析，评价各节点对于整个网络的重要程度，如表2。由表2可知：点度中心性最高的为五里店、重庆西、沙坪坝、冉家坝4个站点，其绝对中心性为6，各有6条边可与其他站点相连，相对中心性为0.850，所占份额为0.007，表示其在网络中的连通性最好，对于网络的顺畅通行具有非常重要的作用；冉家坝站点的接近中心性最大，其绝对中心性为3 734，相对中心性为9.454，与其他所有节点的平均最短距离最小，处于网络中心位置；同兴站点的中介中心性最大，其绝对中介中心性为12 955.924，相对中介中心性为20.854，说明在寻求网络最短路径时经过同兴的次数最多，因此同兴站点有很大的中间作用，对其他节点有很大的信息控制能力。综合考虑，冉家坝、歇台子、礼嘉、重庆西等站点3项指标均处于较高水平，这些节点对网络的正常运行起着至关重要的作用。

表2 中心性指标Table 2 Centrality indicators

4 结 论

以重庆市轨道交通为例，建立其网络拓扑结构模型，并对其复杂网络特性进行分析，获得以下结论：

1)在“十七线一环”重庆市轨道交通远期的复杂网络中，仅有4%的站点只与另外一个站点直接连接，平均1个站点与2.433个其他站点直接连接，平均最短路程需路经13.986个站点，最长线路需经过40个站点。

2)五里店、重庆西、沙坪坝、冉家坝4个站点对网络的连通性影响最大。冉家坝处于网络中心位置，与其他所有节点的平均最短距离最小；同兴为最短路径生成过程中经过次数最多的节点，起着很强的中介重用。综合分析，冉家坝、歇台子、礼嘉、重庆西等站点对网络的正常运行起着至关重要的作用。

根据轨道站点评价结果，在轨道交通的日常管理实践中应当特别关注网络中重要节点的资源配置及站点可靠性，尽可能减少不稳定因素，保证整个轨道交通网络运营工作顺利进行。

笔者通过建立基于二阶张量的非计权网络的拓扑结构模型对轨道交通网络的拓扑结构进行分析，忽略了实际运行中的客流变化、车辆编组、发车时间等因素，而这些因素在轨道交通实际运行中客观存在。因此，接下来可从动态演化过程入手，将车辆编组、发车时间、客流变化、线路及车辆故障等因素作为权重系数加入到分析模型中。