几种预测模型在东海大桥海堤段沉降监测中的应用

黄志文

（上海市市政公路工程检测有限公司，上海市 201108）

0 引言

灰色模型GM（1，1）是用来解决信息不完备系统的数学方法，而时间-沉降预测模型是多年的测量经验总结。本文将应用灰色模型GM（1，1）和时间-沉降预测模型对东海大桥海堤段的沉降数据进行分析处理,以选择合适的沉降模型来预测东海大桥海堤段的沉降趋势。

1 工程概况

东海大桥海堤段的基础地质由淤泥粉砂回填而成，于2005年11月建成通车。由于基础地质的构造以及车辆荷载作用，东海大桥海堤段至2015年年底的最大绝对沉降量已接近1 m，且最大绝对沉降量附近车道出现多个大坑，明显影响行车安全。为了消除行车隐患，海堤段於2016年初进行路面翻修，部分监测点被破坏。通过分析和处理历年海堤段沉降量的数据，构造GM（1，1）模型和时间-沉降模型进行计算，并对模型拟合值和预测值进行比较，以选择适合本工程的预测模型，同时预测出2015年以后每隔10年海堤段大致的最大沉降量，为道路的养护以及海堤的结构安全提供数据参考。

2 模型分析

2.1 GM（1，1）模型

设有等时原始观测数据序列：

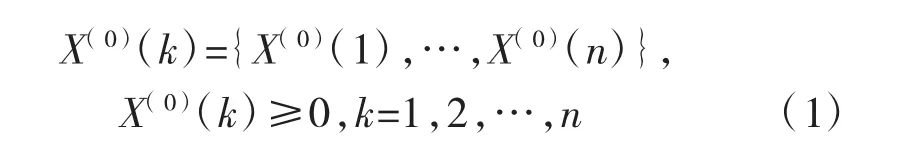
对 X（0）（k）作一次累加，得到新序列：

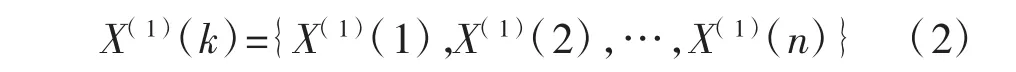
X（1）（k）的 GM（1，1）的白化形式的微分方程[1]为：

GM（1，1）模型的灰微分方程为：

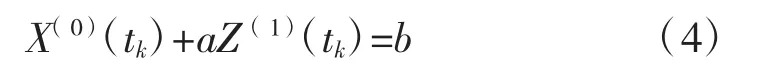
其中：

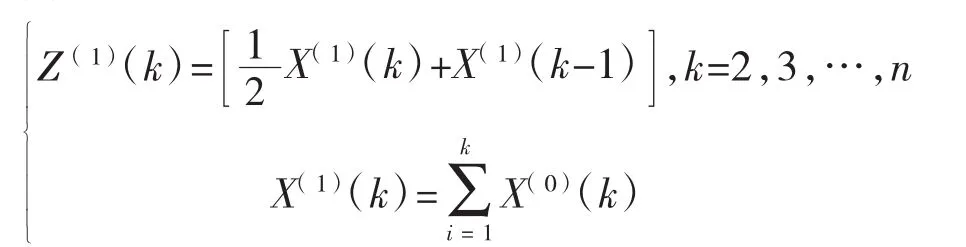
式（3）、式（4）中：a，b 为方程的待定参数；Z（1）（k）为背景值。

其中：

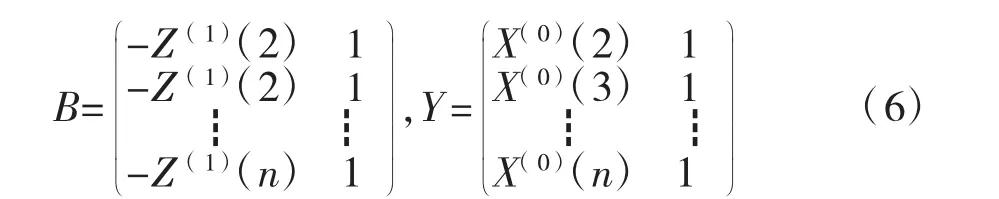
式（3）的离散解为：

原始数据的拟合值为：

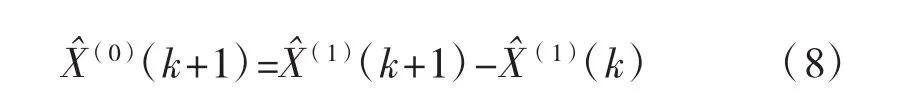
2.2 沉降-时间模型

一般来说，在软土上建（构）筑物的沉降与时间不是线性关系，地基基础人员一般采用下述几种曲线去描述S-T过程（沉降-时间关系）[2]。双曲线：

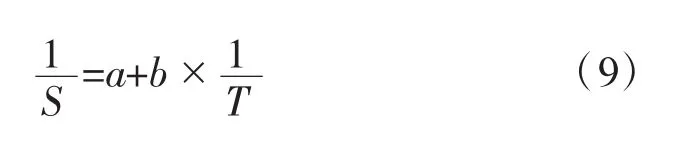
指数曲线：

幂函数曲线：

式中：T为时间；S为随T变化的总沉降量；a、b为方程的待定参数，由最小二乘法求得。

对于以上3种函数，可以通过变量代换，化为可以利用线性回归公式的形式。

对于式（11），令 S3=1n S，T3=1n T，a3=1n a，从而得到：

2.3 精度分析

为了评价预测效果，需对建模进行精度分析。

已知原始观测序列X（0），通过建模计算得到模型拟合值X^（0）的序列为：

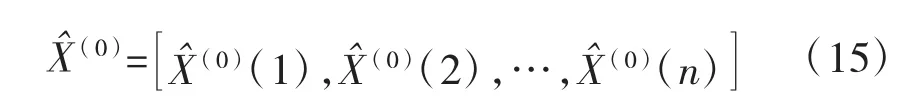
计算残差E得:

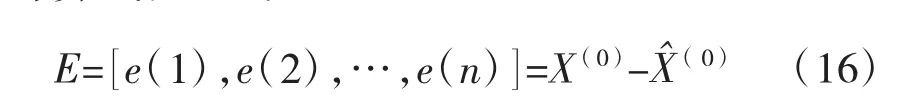
其中:

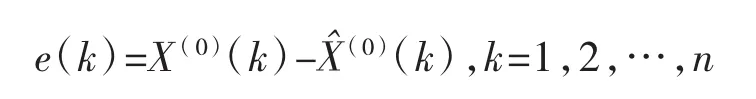
相对误差rel（k）为:

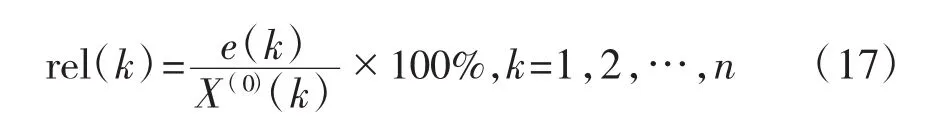
平均相对误差rel为：

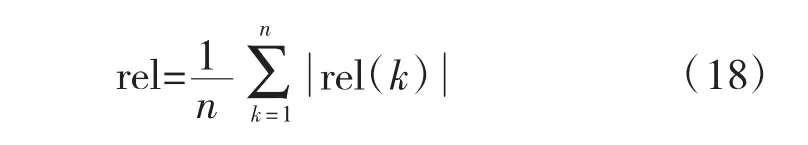
原始观测序列X（0）的方差为:

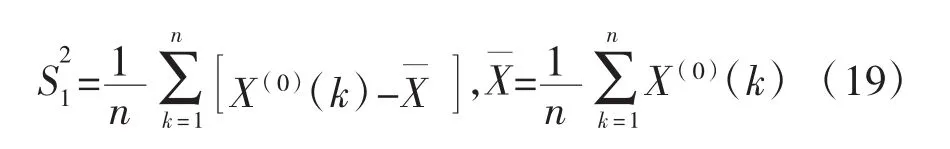
计算后验差比C为：

小误差概率p为：

模型精度检验等级参照表见表1[3]。

表1 精度检验等级参照表

3 实例分析

上海市东海大桥海堤段於2006年11月取初始值，在2007年3月26日开始每月进行定期测量。工程测量范围为上海市东海大桥海堤段K27+579～K29+387，长约1.8 km。本工程测量路线按3条线路进行观测，其中1#和3#线监测点分别布置在道路A、B线应急车道，2#线监测点布置在道路A线中央隔离带位置，监测点间距一般为50 m左右，共布设93个观测点。海堤段沉降监测点布设示意图见图1。

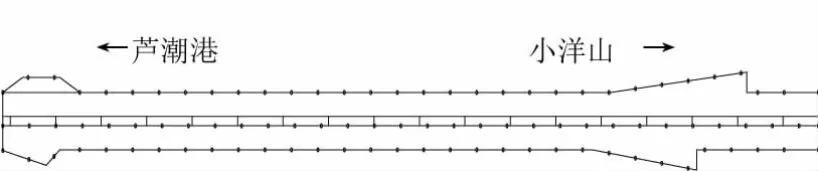
图1 海堤段沉降观测点布设示意图

根据实测资料，选取线路沉降量最大的1#K28+300断面（T13-1），作为沉降代表性的断面进行总沉降量分析。通过原始观测数据进行线性内插获得2007年5月～2014年5月每隔半年（180 d左右）的沉降量，并以此作为分析数据。沉降量原始观测值（绝对值）与模型拟合值见表2。

GM（1，1）模型计算通过 Matlab编程实现，双曲线模型、指数函数模型和幂函数模型通过变量代换，化为可以利用的线性回归公式形式并通过Excel扩展功能实现，最后得出不同模型拟合方程（见表3）；不同模型精度指标、计算精度见表4、表5。

由表4、表5可知，双曲线模型和指数函数模型计算结果与实际沉降观测值偏差较大，而GM（1，1）模型和幂函数模型拟合曲线与实际观测曲线有较好的拟合。拟合结果为GM（1，1）模型拟合最优，幂函数模型次之，双曲线模型较差，指数函数模型最差。

表2 沉降量原始观测值（绝对值）与模型拟合值 mm

表3 不同模型拟合方程

表4 不同模型精度指标

为了进一步分析模型的预测精度和可靠性，用2014年11月，2015年 5月，2015年 11月共 3次的实测沉降量与以上几种模型计算出来的预测沉降量进行比较，以分析各个模型在海堤段沉降预测时的精度和可靠性，并评定各个模型的适用性。不同模型预测值、预测精度、预测精度指标见表 6、表 7和表 8。

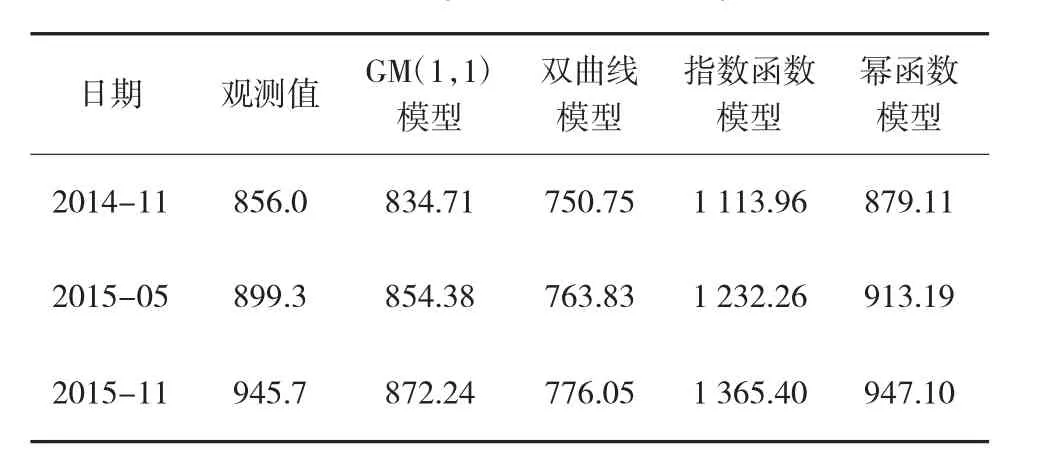
表6 沉降量实测值与不同模型预测值 mm

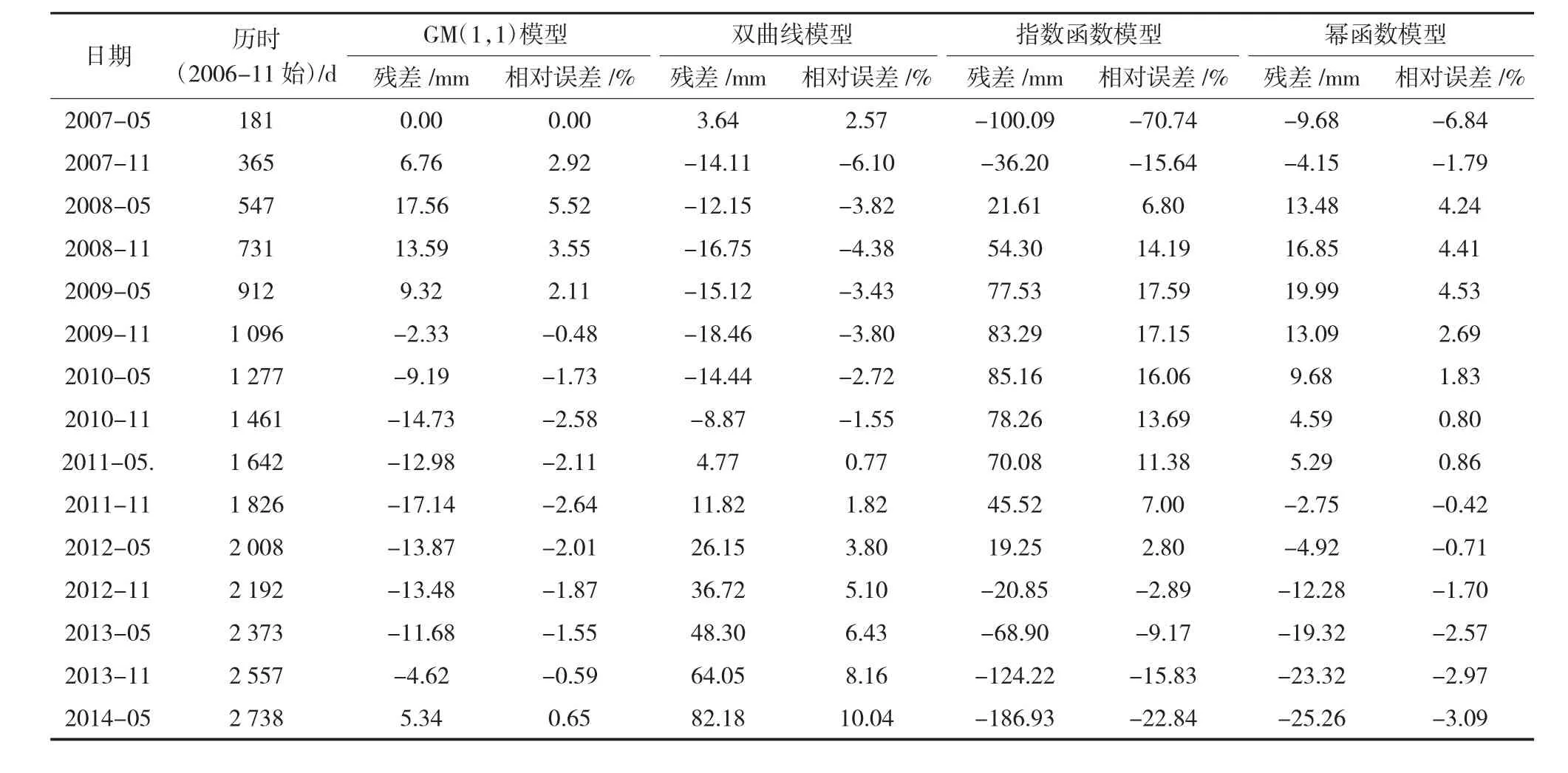
表5 不同模型计算精度

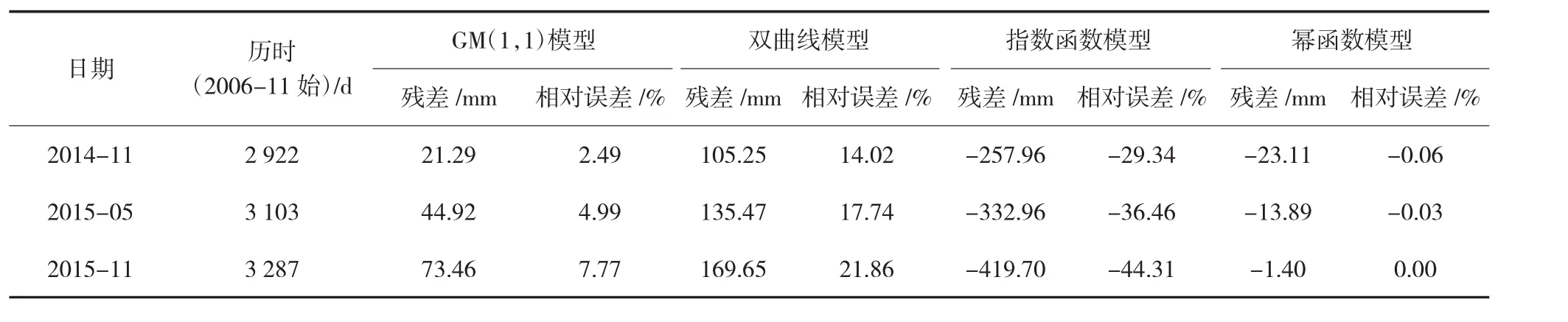
表7 不同模型预测精度

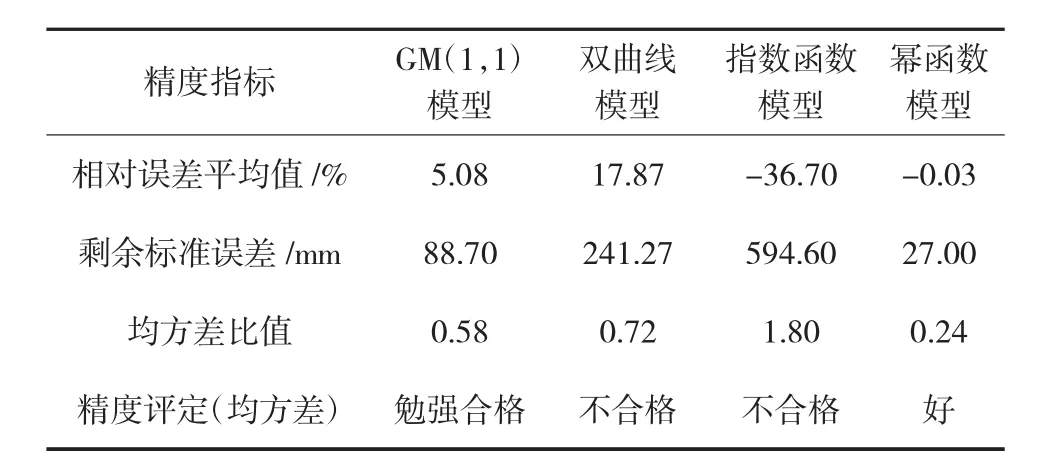
表8 不同模型预测精度指标

从以上几种模型拟合精度结果可知，虽然GM（1，1）模型拟合曲线优于幂函数模型，但幂函数模型可以较好地预测出沉降量，GM（1，1）模型则勉强可以预测出沉降量（残差偏大），说明拟合好的模型预测值不一定好。

通过以上数据分析，选用幂函数模型对海堤段每隔10年的累计沉降量进行预测，结果见表9。

表9 幂函数模型累计沉降量预测值

通过幂函数模型计算最后100 d达到不同沉降速率所需要的时间，结果见表10。

4 结语

（1）结合工程实例，对沉降监测数据进行了模型分析，并在此基础上详细阐述了GM（1，1）模型以及沉降-时间预测模型（双曲线，指数函数，幂函数）的建立。

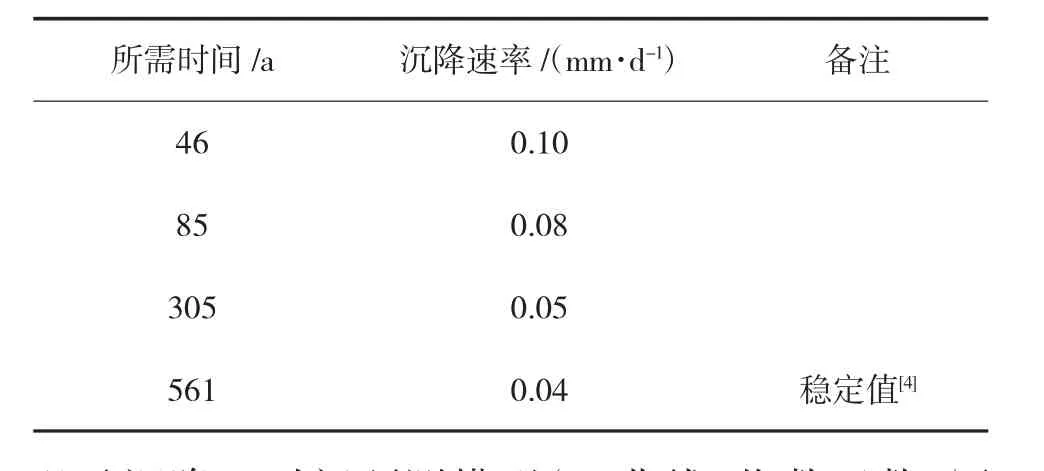
表10 达到沉降速率所需时间

（2）沉降是一个非常复杂的过程，涉及到环境温度、荷载、土层构造、回填材料等许多客观因素影响等导致的沉降机理不确定性，单一模型并不能应用于所有系统的预测。在不同的工程中应选择合适的预测模型，在经过比较分析后，选择其中最适合的一种模型进行预测预警。同时也可以从实际情况出发，考虑建立组合模型进行预测，以提高预测精度。

（3）采用的灰色模型为最基本的 GM（1，1）模型，可通过对GM（1，1）模型进行背景值构造和时间加权等方法提高灰度模型预测精度。

（4）在运用预测模型时要不断根据实测的新数据，建立新的预测模型，以提高預测精度。