两平行载流直导线的磁场能量

杨鹏志 刘嘉豪 杨宏春 邬劭轶 滕保华

(电子科技大学英才实验学院 四川 成都 611731) (电子科技大学物理学院 四川 成都 610054)

1 引言

长直载流导线是电磁学中的一种常见理论模型[1]，并且在大学物理习题中也经常被讨论．比如大学物理中经常有这样的问题：

【题目】两根无限长的平行载流直导线，其间距为a且电流反向，如图1所示，在保持电流I不变的情况下增大平行导线的间距，则空间总磁能将如何变化[2]？

图1 平行长直载流导线示意图

对这类问题通常可以采用做功和等效自感的方法进行定性分析．

若用简单做功方法，则是类比带异种电荷的平行板电容器的情形[3]．当增大两板间距时，需外力做功，则电场能量增加．类比此问题，表面上看，两导线相互排斥，当增大两导线间距，外界做负功，则磁场能量减小．但是这个结论与真实情况相悖，因为这里没有考虑导线中感应电动势的影响[4]，而此时电源克服感应电动势做功又很难定量计算．

若用等效自感方法，经过解析推导，可以得到两长直导线中轴线内侧的单位长度自感系数(忽略两导线中心轴线以外的磁场)为

其中μ0表示真空磁导率，a和r分别代表导线轴心间的距离和导线半径．再结合磁场能量公式

可以发现，当增大导线间距a时，自感系数L变大，则磁场能量Wm增大．这与正确结果一致，但是该方法又无法应用于同向长直载流导线的情形．

综上所述，简单地利用做功方法往往会得到错误的结果，而用等效自感方法又不能处理电流同向的情况，因而导致此类问题缺乏统一合理的解决方案．

本文则从磁场能量密度和总磁能的角度出发，对这类问题进行理论分析，从而得到合理直观的统一解释．

2 模型建立

如图2所示，假设导线A与B轴线间距为a，导线半径为r．

图2 电流反向情况下导线外部磁场的矢量叠加图

由于该平行长直导线磁场具有上下平移不变性，故将沿导线方向单位高度内的空间磁场能量求解转化为平面问题．又因为磁场能量密度的原点对称和轴对称性，所以只在第一象限进行计算分析．

下面分两种情况进行讨论.

2.1 电流反向情况

设

(1)

于是第一象限内两根载流导线外任意一点M(x,y)点的磁感应强度分别为B1和B2

(2)

从而第一象限内，导线外M(x,y) 处两载流导线的磁感应强度的矢量叠加，即总磁场为

(3)

根据磁场能量密度与磁感应强度关系，得到第一象限内载流导线外的两载流导线总磁场能量密度为

(4)

其中

同理，第一象限内两载流导线在导线A内部任一点(x,y)处的磁感应强度分别为B3和B4

(5)

从而第一象限内，导线A内(x,y) 处两载流导线的磁感应强度的矢量叠加，即总磁场为

(6)

于是载流导线内的总磁场能量密度为

x2(r2-v)2}(8π2r4v2)-1

(7)

其中

2.2 电流同向情况

通过与反向通电导线相似的推导，第一象限导线外和导线内的总磁场能量密度分别为

(8)

x2(r2+v)2}(8π2r4v2)-1

(9)

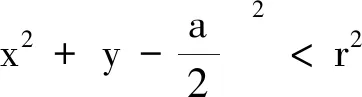
3 结果与讨论

为了更加清晰地分析此问题，下面首先来看磁场能量密度的分布情况．

利用Mathcad仿真，可以分别得到电流反向情况下垂直电流方向的截面内磁场能量密度等值线(图3)、三维图(图4)，以及二维截面图(图5)，这里的参数设定为

r=0.001 m

a=10r

并定义下列约化磁场能量密度和约化磁场能量

图3 电流反向情况下磁场能量密度等值线

图4 电流反向情况下磁场能量密度三维图

从图3和图4可以看出，在两根导线外围某些位置，磁场能量密度取峰值，而偏离那些位置时，不论是载流导线内部还是外部，磁场能量密度都是快速下降，甚至趋于零，同时磁场能量密度具有较好的对称性．

再看磁场能量密度的二维截面图，也就是在平行于y轴做一系列参考线的分布图，如图5所示．

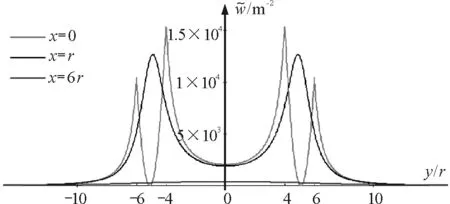
图5 电流反向情况下磁场能量密度二维截面图

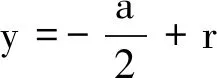
但是当参考线位置为x=r和x=6r时，磁场能量密度分布发生了明显变化，极大值点不断减少，且曲线更为平坦并且最后能量密度趋于零．图5告诉我们，不同参考线上的磁场能量密度峰值存在四峰、双峰和单峰的情况，但是随着参考线位置不断向外移动，两组双峰不断接近，在x=r参考线处四峰合为双峰，之后这一组双峰又在不断接近，最终变成单峰．

电流同向条件下的磁场能量密度等值线和截面图的情形与反向情况类似，具体细节如图6和图7所示.

图6 电流同向情况下磁场能量密度等值线

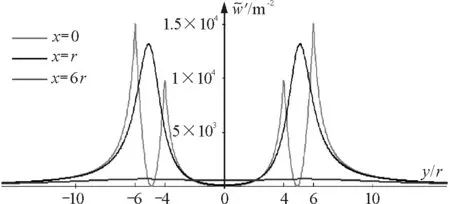
图7 电流同向情况下磁场能量密度截面图

根据以上讨论的磁场能量密度，可以计算在沿导线方向单位高度构成的空间区域内的总磁场能量．首先计算第一象限中载流导体内的能量

(10)

(11)

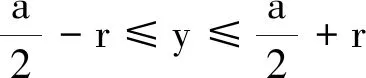
(12)

(13)

考虑到磁场能量密度的对称性，于是得到整个空间区域(4个象限)内的总磁场能量为

E(a)=4[E1(a)+E2(a)+E3(a)+E4(a)]

(14)

从而磁场能量和导线间距的关系可以统一地通过数值计算得到，图8是使用Mathcad软件对磁场能量E(a)进行数值计算的结果．

图8 电流反向情况下磁场能量随导线间距a变化

同理得到电流同向时的总磁能E′(a)和导线间距的关系如图9所示.

图9 电流同向情况下磁场能量随导线间距a变化

从图8可以看出，若平行导线中电流反向，则增大两导线距离时磁场能量增加，但是增大的趋势不断减缓．而从图9可以看出，若平行导线中电流同向，则随着导线距离的增大，磁场能量将会减小，但是减小的趋势同样地不断趋缓．

4 结束语

本文以平行载流直导线的磁场能量分布这个大学物理课程中的基本问题为案例，通过解析计算两根平行长直载流导线的磁场能量密度分布，以及数值分析沿导线方向单位长度空间内的总磁能，给出了此基本问题的一个合理直观的理论描述．