地震和降雨作用下的填土边坡室内模型试验研究

田松何

(中国建筑第六工程局有限公司，天津 300450)

滑坡事故一直以来都是造成生命财产损失的重要地质灾害之一，近年来由于基础设施的快速建设，边坡失稳问题逐渐成为了研究的热点。影响边坡稳定的因素有很多，其中降雨和地震便是触发边坡失稳的两大重要因素。如1972年6月中国香港地区发生了长时间的强降雨，降雨强度一度达到65 mm/h，强降雨导致的滑坡事故造成了250人死亡，其中大量房屋被掩埋，仅秀茂坪[1]的一处滑坡就造成71人丧生。云南省昭通市小坝村[2]于2009年4月因强降雨而触发了山体滑坡，滑坡的岩土体总体积达到8 000 m3，其长约50 m，宽约40 m，厚度更是达到4 m，由此造成了20多人的伤亡。2015年12月，红坳渣土受纳场[3]由于地下水的缘故发生了滑坡，造成了73人死亡，大量厂房被掩埋，由其造成损失高达8.81亿元。1976年的唐山大地震[4]造成了密云水库的大坝土体液化进而导致坝体滑坡。2008年，汶川发生了8.0级大地震，此次地震造成了大规模的滑坡和泥石流，造成失稳的边坡多达2万余处[5]，此次造成的边坡失稳规模也是十分罕见的，其中安县大光包滑坡规模创下了历史之最，居世界之冠[6]。一直以来，相关学者对地震和降雨单独作用下的边坡失稳问题做了大量的研究，但是针对地震和降雨共同作用对填土边坡稳定性影响的研究却很少见于报端。赵川、付成华等[7]基于局部强度折减法基本理论,采用有限元软件对某含有软弱夹层的水电边坡进行稳定性分析评价。马紫娟 、张有龙等[8]利用有限元软件Geostudio分析了降雨持时、降雨强度、地震时程3个参数对边坡的稳定性影响。李晓莲、余云燕等[9]利用FLAC3D数值软件分别计算并分析了降雨单独作用、地震单独作用及降雨与地震共同作用条件下边坡应力场、位移场、塑性区及剪应变增量的变化。王兰民、蒲小武等[10]开展天然状态、降雨100 mm黄土边坡2种模型的振动台试验，分析了边坡模型的宏观变形、加速度、孔压、土压力等相关物理量的变化特征。本文采用自行制作的可以模拟降雨和地震的试验装置进行模型试验，对地震和降雨共同作用下的边坡动态响应和坡面形态变化进行了分析。

1 试验装置简介及模型边坡的制作

1.1 试验装置简介

试验装置主要包括试验模型箱、振动台、人工降雨系统、量测系统等部分[11]。模型箱设计长度为2 m、宽度为1.5 m、高度为1.8 m，采用钢板及角钢制成，此外为了能够从侧面观察模型箱内的边坡模型的裂纹、位移、浸润峰的发展情况，将模型箱的两侧壁改成透明的有机玻璃。振动台最大载重量为6 t，最大工作频率为20 Hz,满载下的最大加速度和位移分别为1 g和±150 mm，其运动方向为水平向平动。人工降雨系统主要包括供水设备、降雨喷头及其组合装置两个部分。降雨喷头采用喷嘴式，根据其口径大小分为3.0、3.5、6.5 mm 3个型号。为了对降雨强度和降雨范围进行有效控制，对原本固定喷头位置的降雨设备进行了改进：降雨强度主要是通过降雨喷头型号的选择、降雨喷头的数目、降雨喷头间距3个因素组合控制；降雨范围通过降雨喷头的固定间距控制。

1.2 模型边坡的制作及试验工况的设计

1.2.1模型边坡的制作

在边坡模型填筑前需要对模型边坡填土的物理力学参数进行测定，测得的边坡填土为粉质黏土，具体的参数见表1。

填土边坡模型的填筑采用梯形分层填筑的方案，共分为10层，每层10 cm，然后通过厚度、面积、体积计算需要填土的质量，按照设计好的削坡位置进行削坡。用彩笔在有机玻璃上作边长为10 cm的正方形网格，作为坡体位置参考，便于观察示踪点移动、湿润峰变化以及裂缝相对位置和发展情况。边坡填筑时的模板支护应从下往上，支撑牢固，不能出现松动和漏洞情况，防止土体流出，压实度达不到设计要求。削坡时，模板的拆除应从上往下依次拆除，拆完模的上部土体应避免再次扰动。同时边坡填筑过程中，将传感器按相应的设计方案埋设在土体中，传感器的具体位置见图1。

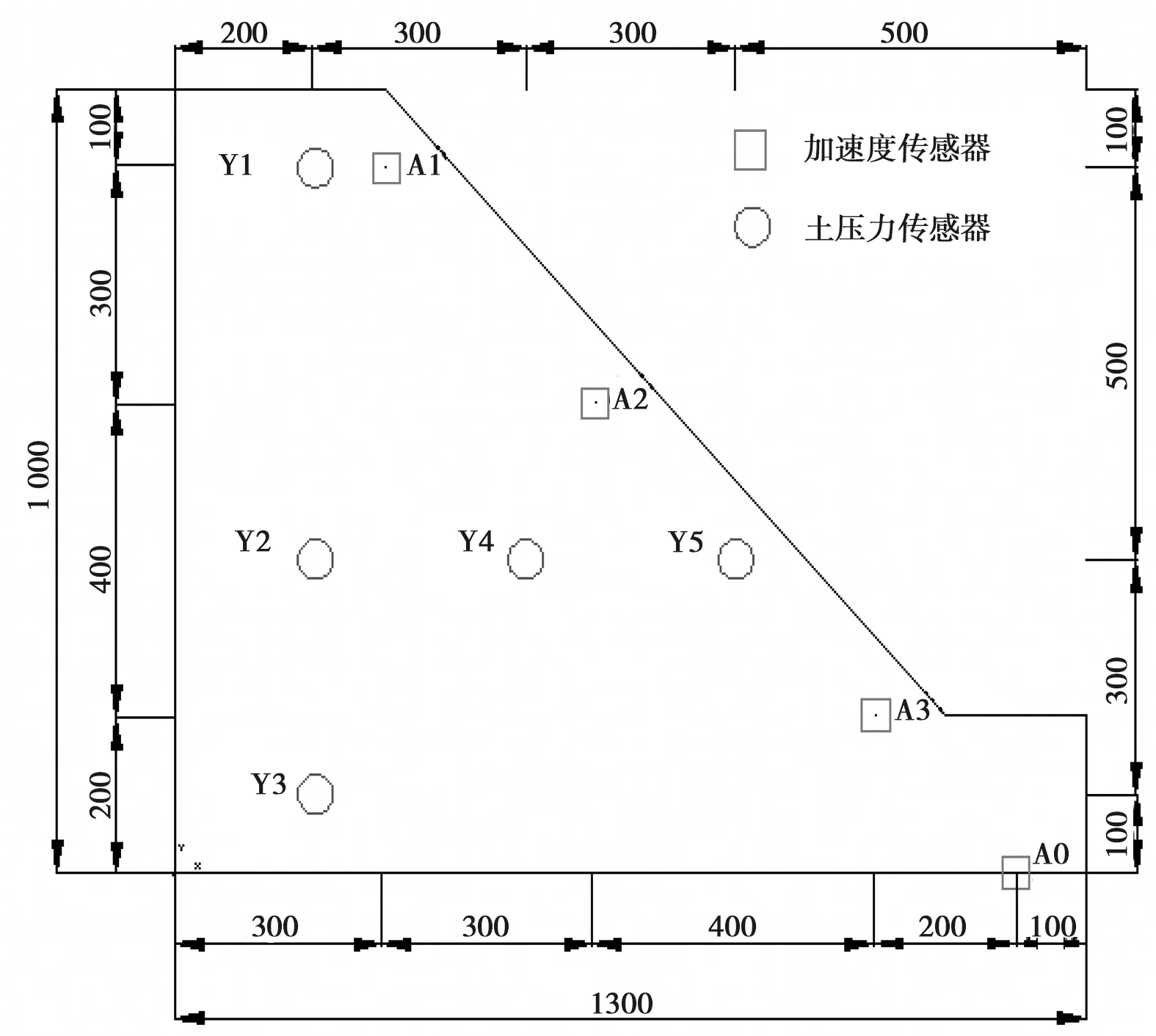
图1 传感器布置

1.2.2试验工况的设计

地震波类型本文选取的是El-centro波和Kobe波。最终地震作用下的边坡模型试验的加载制度拟采用表2的加载制度。编号WTN、ELC、KOB分别代表白噪声随机波、El-centro波、Kobe波。边坡模型在地震作用加载后会进行降雨作用。

表2 振动台模型试验加载制度

2 地震和降雨物理模型试验及其结果分析

本次边坡模型试验是先进行不同工况下的地震作用，在不损毁边坡模型的前提下，探讨边坡模型的裂纹裂缝的发展情况，并监测边坡的土压力和加速度的动态响应情况。地震作用试验完成后，间隔2～3 h，使土体内部应力分布均匀后进行降雨作用，试验过程中，对浸润面和坡面的形态变化进行详细记录，在此基础上分析边坡在地震和降雨共同作用下的动态响应及变形机制。

2.1 地震作用下的试验结果分析

在进行降雨试验前先进行地震试验，本次地震的加载制度见表2。本次试验的地震波输入均为水平方向，暂不考虑竖直向。地震波的波形共3种，分别为白噪声随机波(持续时间150 s)、El-Centro波(持续时间40 s)、Kobe波(持续时间40 s)。

2.1.1加速度响应

前人在边坡模型试验中做了很多有关动力响应的研究，其中对加速度响应描述的一个重要指标便是PGA放大系数。由图2a可知粉质黏土在不同峰值加速的El-Centro波作用下的PGA放大系数，从图中可以知道坡面对地震波的加速度响应随位置不同而表现出不同现象，其中坡顶A1处响应最强，其次是坡中A2处，三者之中响应最小的位置是坡脚A3处；从图2a还可知峰值加速度在0.1～0.3 g区间内边坡的加速度响应随着地震峰值加速度的增大而增大，0.1 g时加速度响应最小，0.3 g时加速度响应最大。图2b表现出和图2a相同的变化趋势，即随着加速度的增大响应强度增强，但是图b中的边坡在峰值加速度为0.1 g的El-Centro波作用下的加速度响应要大于经过若干次加载后的同样为0.1 g的El-Centro波作用下的加速度响应，通过若干次的加载后边坡出现了损伤，有裂缝、位移等情况发生，故其对边坡的响应规律造成的影响。由图3可知坡面在同一峰值加速度不同地震波作用下，粉质黏土边坡同一位置表现出相似的变化规律，即随着峰值加速度的增大边坡的响应规律逐渐增大，El-centro波近似为线性增长，而Kobe波则在0.1 g之前增长较慢，而在0.1～0.15 g之间增长变快。值得注意的是边坡在峰值加速为0.08 g的Kobe波作用下加速度响应均小于1，也就是此时边坡的加速度响应小于水平地震波的输入。

a)0.1～0.3 g

b)0.05～0.15 g图2 坡面在不同峰值加速度作用下的PGA放大系数(El-centro波)

2.1.2土压力响应

本文按照表2的试验加载制度进行了试验边坡水平方向的土压力的测试，以ELC-1为例进行了振动台试验，试验边坡的同一竖直方向和同一水平方向水平土压力的响应规律见图4。从图5a可知，在0.08 g的El-centro地震波作用下，同一竖直方向的X-土压力表现为：坡底响应最小，随着高度的增大，土压力大小逐渐增大，在边坡中部某一点达到最大值，然后随着高程的增大，X-土压力逐渐减小，但坡顶的响应仍然要大于坡底。从图4b还可得出，在0.08 g的El-centro地震波作用下，试验边坡0.4 m高度处的X-土压力随着坡内向坡面水平移动，会出现逐渐减小的趋势，且减小的幅度逐渐减小。从边坡模型宏观分析可知，边坡模型后壁给边坡模型提供了向前移动的推力，而边坡模型对该推力有逐渐削弱的作用，离后壁越近削弱的程度越大，越远力度越小，这和图4b所示的曲线斜率逐渐减小相一致。由图5可知，在地震峰值加速度相同的情况下，填土边坡对Kobe波的地震响应规律与El-centro波相同，但是填土边坡对El-centro波的响应要略强于Kobe波。图6中的ELC-4、ELC-5、ELC-6分别为试验设计方案中的0.1、0.2、0.3 g地震作用，从图6a、6b可知，同一位置处，随着地震波峰值加速度的增大，其对应的X-土压力响应也逐渐变大。从中还可得知，同一地震波作用，在同一竖直方向上，坡底的X-土压力响应最小，坡中的某位置最大，坡顶次之；而在同一水平方向上，随着作用位置离坡面越近，其X-土压力逐渐减小，即坡后壁处最大，坡面处最小，模型边坡对X-土压力具有削弱作用，这些规律也和上面的试验ELC-1、Kob-1结果相一致。

a)A1

b)A2

c)A3图3 坡面不同位置在相同峰值加速下的响应规律

a)竖直向土压力的响应规律

b)水平向土压力响应规律图4 ELC-1地震波作用下边坡模型的X-土压力响应

a)竖直方向

b)水平方向图5 峰值加速度为0.08g作用下的土压力响应

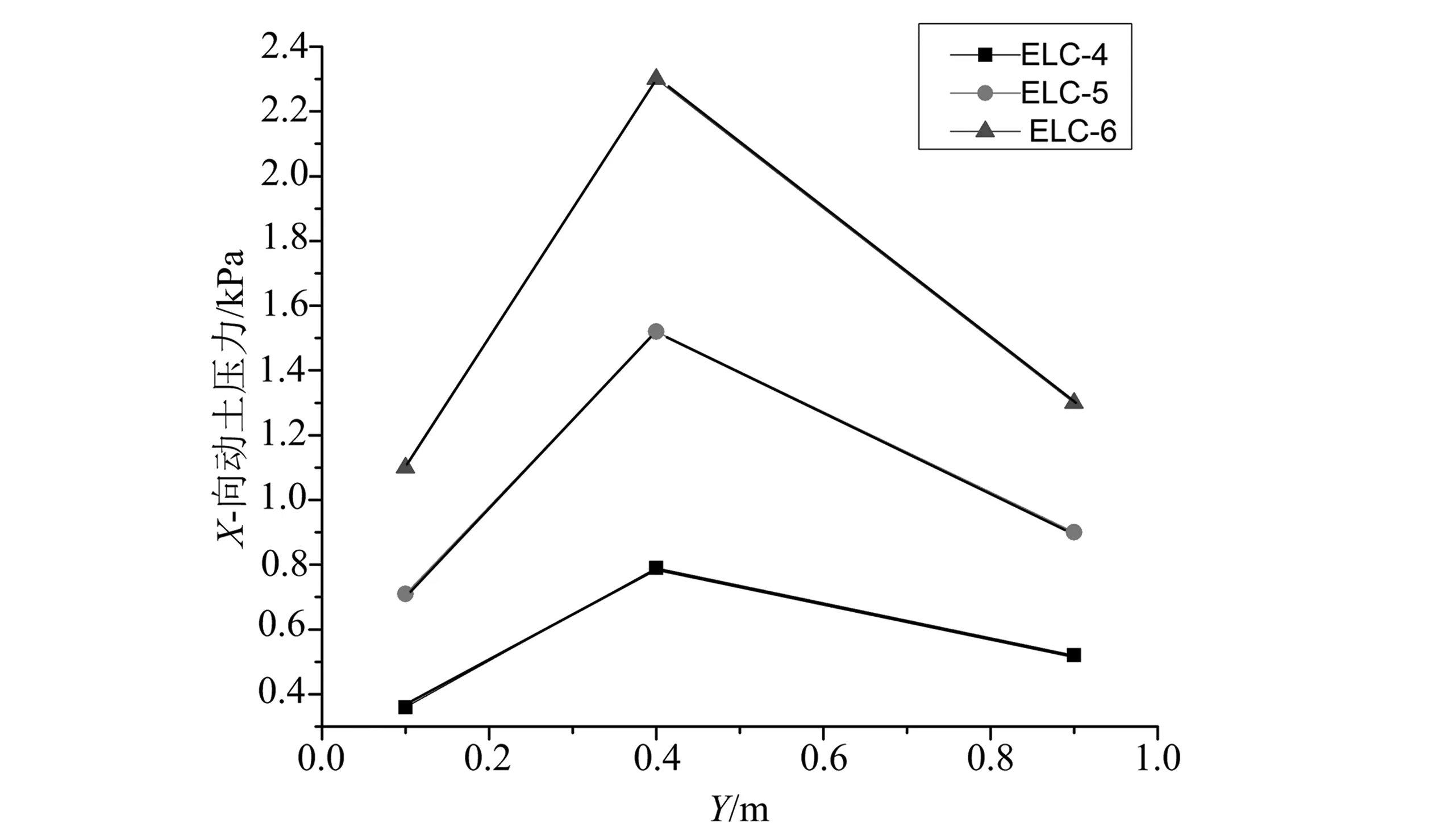
a)竖直方向的X-土压力响应

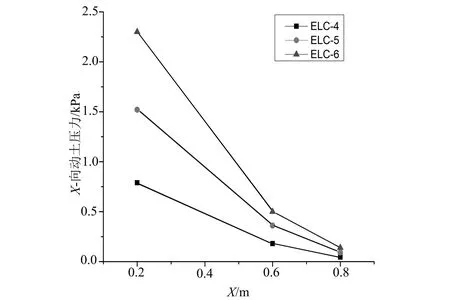
b)水平方向的X-土压力响应图6 不同峰值加速度作用下的土压力响应规律

2.1.3模型边坡的侧壁和坡面的裂缝和位移发展情况

为了比较直观地测量出模型边坡在振动台实验中的位移和裂缝发展情况，本次试验采用的是在边坡侧壁、坡面以及坡顶埋置标志点并利用网格线辅助测量的方法。在边坡模型填筑好之后进行了试验编号为ELC-1、KOB-1、ELC-2、KOB-2的地震试验，由于输入的地震波峰值加速度较小，边坡始终呈现稳定的状态，其侧面及坡面均无裂缝和位移发生，坡面只出现零星的散土颗粒滚落。试验进行到KOB-3时模型边坡在坡顶后缘处出现明显的整体下陷情况，下陷的最大深度为3 cm，此时的模型边坡的侧面也发生位移，具体情况见图7。从图7a可以看出模型边坡的顶部出现下陷情况，边坡的顶部与红色分层线的最大距离达到3 cm，但顶部未出现裂缝。在图7b中透过有机玻璃可以看到编号为1的2个橡皮塞随着地震动出现了移动现象，其橡皮塞的最大移动距离为6 mm，其运动方向为向右偏上一点，由于橡皮塞的密度与土相近，因而可以将橡皮塞的运动情况代表模型边坡土的运动情况。从图7b中的编号2、3处可知边坡的坡顶前缘和坡面中上部在地震动过程中出现下陷状况。随着模型试验的进行，在编号为ELC-4时边坡顶部出现了裂缝。裂缝在左右两侧同时出现，且都向坡顶中部发展，在编号为ELC-5试验时整个拉裂缝在坡顶横向贯通，见图8。在坡顶拉裂缝出现的同时坡面也出现了斜向上的剪切裂缝，坡面裂缝首先出现在填土之间的分层界线处，此处由于是边坡两层土之间的衔接处，故而应力分布不是很均匀，抗剪切的强度要小于其他地方。在地震发生时，坡面的该薄弱地方率先出现裂缝并且斜向上发展，在编号为ELC-6试验时出现坡面横向贯穿，见图9。综上可推知，填土边坡的滑坡形成是从坡顶出现横向拉裂缝开始，然后坡面中部某位置出现剪切破坏的斜裂缝，紧接着坡顶处的拉裂缝向下发展，坡面的剪切裂缝向坡体内部发展，直至两处裂缝贯通，形成滑裂面，进而促使边坡发生滑坡事故。

2.2 震后降雨作用下的试验结果及其破坏模式分析

本次试验按照图10的工况进行了降雨，在打开阀门降雨强度会有稍微的波动，但在每小段降雨时间内可近似认为降雨强度是均匀不变的。在本次降雨模拟试验中对边坡模型相关变量进行了测量和分析，分析结果如下。

a)坡顶下陷

b)边坡侧壁位移及下陷图7 模型边坡的位移及下陷情况

a)坡顶裂缝图8 坡顶裂缝的发展状况

b)坡顶右侧裂缝

c)坡顶左侧裂缝续图8 坡顶裂缝的发展状况

图9 坡面裂缝的发展情况

图10 模型试验降雨历程

2.2.1浸润峰入渗速率及形态变化

在模型边坡进行完地震试验后，进行降雨试验，在前5 min内，由于模型边坡试验用土的渗透系数较大，一开始的入渗速度大于降雨强度，致使雨水全部渗入，坡面未出现坡面径流。随着降雨的进行，边坡坡面处的土壤逐渐趋向饱和，在入渗速度小于降雨强度时便出现了坡面径流，本次试验在7 min左右便出现了坡面径流。此外随着雨水的不断入渗，模型边坡的土壤随着含水量的增大，土壤的颜色逐渐变深，而深色浅色土壤的边界便出现了浸润峰。本次试验通过架设在边坡模型有机玻璃侧的摄像机拍摄浸润峰的变化情况，以此来判断和计算雨水的入渗深度和入渗速率。

图11是选取不同降雨时间段的浸润峰图片，其中图11a、11b显示浸润峰首先出现在坡顶和坡面且不断向内部推移。图11c、11d则反映随着降雨的持续，坡顶的雨水一部分入渗，一部分形成坡面径流，而其中还有一部分沿着模型箱后壁入渗，由于后壁和土壤的材质不同，入渗的速度要大于土壤，故而浸润峰在后壁处很快竖向贯通，在竖向贯通后随着含水量的增大，便沿着水平向向边坡内部入渗。从图12可以看出坡顶和坡面的雨水入渗速率还是具有一定的规律性的，从图上可以看出不管是坡顶还是坡面入渗速率总体还是呈现相同的减小趋势，这是由于随着降雨的进行，入渗的雨水使土壤的含水率不断增大进而使表层土趋向于饱和状态，入渗速度逐渐减小，而在饱和后表层土的入渗相对较小且稳定，而内部由于渗入的雨水量较小，进一步降低了雨水的入渗速率。此外，可以看出32 min是坡面和坡顶入渗速率曲线的交点，在32 min之前坡顶的入渗的平均速率要比坡面大，这是因为一方面坡顶在地震作用时产生了数条细裂缝，入渗的雨水正好可以沿着裂缝快速深入；另一方面随着降雨的进行在坡顶处形成了积水，这一因素又促使入渗速度加快，相对于坡面处于倾斜角度，多余的雨水都形成了坡面径流流向坡脚。而在32 min之后坡面的雨水平均入渗速率要略大于坡顶，这是由于随着降雨的进行坡脚处出现了大量积水，且坡脚的积水量远大于坡顶。而后期降雨的入渗速度有所提升，这是因为后期增大了降雨强度，进而加速模型边坡的破坏速度。

a)t=5 min

b)t=116 min

c)t=134 min

d)t=166 min图11 模型边坡的浸润峰位置

图12 边坡模型降雨入渗速率

2.2.2模型边坡滑坡坡面形态变化

粉质黏土边坡的降雨破坏过程见图13，在形成表面径流的同时，强降雨使边坡表面形成了暂态饱和区，暂态饱和区处的土壤由于饱和度较高，在水分的作用下表层土壤一方面抗剪强度变弱，另一方面其土体容重增大下滑力增大，故出现了轻微的流滑现象，流滑的土壤在强降雨的冲刷下以及表面径流的运移作用蓄积在了坡脚(图13a)。由于发生流滑的地方其土壤率先达到暂态饱和状态，其饱和区呈现一块块独立的区域，流滑发生后边坡表面于是出现了一块块的片蚀现象。片蚀的形成主要是由于雨水自上而下降落对坡面产生的溅蚀作用，溅蚀使边坡坡面松散的土颗粒产生了运移，再加上土体含水量的增大，絮结成一块块的流滑体，在表面径流的作用下流向了坡脚。片蚀之后随着降雨入渗和表面径流路径的稳定，在坡面中间率先出现了沟蚀现象，而坡面两侧的面蚀逐渐加大，见图13b。随着降雨的持续，坡顶和坡面都出现了土颗粒运移现象，直观的表现就是坡顶和坡面都出现了洼地和坡顶转角下陷。从图13c可以看出地震时产生的细裂缝在降雨的过程中在不断扩大，不管是深度和宽度都得到了进一步的发展。从图13d可知，降雨的持续进行，冲蚀沟的沟蚀作用进一步发展，冲蚀沟在径流的冲刷下向更深的土体和两侧土体发展，此外坡面的两侧的冲刷沟逐渐增多起来。图13e可以看出，冲刷沟在向深切和侧蚀发展的同时，其长度也在不断的发展，逐渐贯穿坡面。图13f可知，冲蚀沟沿坡面的纵向发展正好经过坡顶的裂缝处，这是由于坡顶拉裂缝的形成，加速了附近土体趋向饱和的速度，饱和的土体由于土体容重的增大和抗剪强度的降低，再加上雨水的冲刷，率先发生流滑进而发展成沟蚀，最终与坡面的冲刷沟相连，造成边坡的彻底破坏。根据本次降雨模型试验现象和前人的试验总结可以判定本次降雨试验在降雨强度较高的情况下为浅层流滑型滑坡破坏。

a)t=30 min

b)t=40 min

c)t=64 min

d)t=124 min图13 模型边坡滑坡的发展过程

e)t=154 min

f)t=166 min续图13 模型边坡滑坡的发展过程

3 结论

a)地震工况下，本文用的粉质黏土边坡在El-Centro波作用下得到的结论有：①通过PGA放大系数可以判断边坡模型的加速度应从下往上逐渐增强；②同一竖直方向下的X-土压力表现为坡底的响应最弱，随着高度的增大X-土压力响应逐渐增大，在坡中达到最大值，随后逐渐减小，在0.4 m高度处的X-土压力响应随着坡内向坡面水平移动，响应呈现为逐渐减小的趋势；③振动后，坡顶率先出现了横向裂缝并且土体有下陷的情况，同时在某个时刻坡面中部薄弱位置会出现剪切破坏的斜裂缝，紧接着是坡顶处的拉裂缝向下发展，而坡面的剪切裂缝向两侧和坡体内部发展，直至两处裂缝贯通，形成滑裂面，进而促使滑坡事故的形成。

b)震后降雨工况下，本文试验时的降雨强度是大于125 mm/h的强降雨，试验得到的结论有：①通过降雨入渗速率的统计和分析，可知坡顶、坡面的平均入渗速率是总体呈现减小的趋势，此外32 min之前坡顶下方的平均入渗速率要大于坡面下方，而32 min之后，则坡面下方的平均入渗速率要大于坡顶；②降雨时，模型边坡的坡面首先在暂态饱和区出现流体，紧接着向片蚀发展，进而到沟蚀，最终形成多条贯穿坡面的冲蚀沟致使坡面发生破坏。