西洞庭湖南咀站月平均流量估算模型对比研究
伍佑伦,易放辉,刘晓群,宋 雯,吕慧珠,赵文刚
(1.湖南省水利水电科学研究院,湖南 长沙 410007;2.湖南省水利厅,湖南 长沙 410007)
河道径流量分析与预报研究对于合理开发、利用水资源具有十分重要的意义[1-3]。通常情况下,径流过程受流域下垫面、气象、植被以及人类活动的综合影响,表现出非线性、非平稳性且具有大量不确定性、随机性和高复杂性[4]。国内外常见的径流中长期预测、估算方法以基于数理统计的回归分析[5]、SWAT模型[6]、基于质量、能量守恒的水量平衡模型[7-8]、人工神经网络算法为主。一直以来水利工程修建、植被破坏等人类活动对径流过程的影响越来越明显,传统回归分析法在处理长系列水文资料时,对于人类活动影响较大的径流过程无法进行还原计算,难以保证水文资料的一致性;水量平衡模型研究站点分布跨度较大、中间临时性取水活动较多、基础资料不齐全的站点时精度往往受限,使其在实践中难以推广;SWAT模型径流研究中需要输入研究区域土壤类型、地形等资料等众多资料,参数难以确定。除此之外,以上方法预测过程中对于径流的随机性规律很难清晰准确把握[9]。
目前,神经网络算法由于其非线性特点,所以广泛应用于径流预测,且常与其他方法耦合使用。鉴于影响径流因素众多,因子间相互联系,导致预测精度、泛化能力较差,通过(核)主成分分析法能够去除噪音、减少输入参数,与PSO、SVM、BP等算法结合能建立相对简化的径流预测模型[10-11]。除去影响因子众多,径流过程自身复杂性又是数据驱动预测模型的难点。小波分析对长序列径流数据解构能有效识别主频、局部信息与SVM等算法强泛化能力配合在中长期径流预测中能提供一定参考[12-13]。但在气象、下垫面、人类活动共同作用下形成的径流非线性非平稳序列,其小波分析基函数凭经验难以查找,经验模态分解法(EMD)自适应以观测数据为基础,将径流序列分解成若干高频至低频信号及残差,通过神经网络算法依次预测,进而重构径流序列[14-15]。与其他方法配合使得神经网络预测径流精度有所提高,但其物理意义仍不十分明确。
本文借助EMD分解方法能同时在时域和频域内得到较高的分辨率,从水文时间序列中发现有序、确定性的内在规律,揭示径流复杂的运动特征,给予各分量明确的物理意义,并结合常用神经网络算法建立合适的径流估算模型。
1 研究概况
西洞庭湖是洞庭湖西部咽喉,吞吐长江松滋、太平二口洪水,承接沅、澧二水,纳沧、浪等八河入湖,是长江中下游洪水的首个“承接器”和防旱“前哨站”;同时,也是江湖复合湿地生态系统的典型代表与调节器,具有强大的自然调蓄洪水功能,是构建洞庭湖湿地乃至长江中下游湿地安全体系的重要战略要地。区内拥有河流、湖泊、沼泽、人工湿地等多种湿地生态类型,水系发达,“涨水为湖,退水为洲”是其主要特征,自20世纪90年代以来共发生1995、1996、1998、1999 年累计5次特大洪水。南咀站作为西洞庭湖的重要水文站点,控制松澧洪道和沅水经西洞庭湖湖口(北端)流入南洞庭湖水情的重要控制站,其上游的松滋-太平水系建有控制性水文站点安乡站,澧水水系建有控制性水文站点石龟山站[16-17]。
2 数据来源
依托长江水利委员会荆江水文水资源勘测局、湖南省水文局收集1956—2008年石龟山、安乡站月平均水位(Z)、流量(Q)数据,南咀站月平均流量(Q)的水文资料,结合多元回归法对缺测数据进行插值补齐。
3 研究方法
本研究以南咀站月平均流量作为基准值,经验模态分解(EMD)后结合BP、小波神经网络(WAVE)、广义回归神经网路(GRNN)估算南咀站月平均流量,研究其在南咀站的适用性。
经验模态分解是一种非线性非平稳信号的分析方法,因其具有多尺度分析、基函数由自身构造的特点。广泛应用于海洋、大气、天体观测资料与地震记录分析等模态参数识别方面,河道水位、流量随季节、气象及上下游变化一定程度上也呈现出非线性。因此,本文引入EMD方法进行南咀站流量估算[18]。
同时鉴于河道水位、流量作为一种水文现象,其既有确定性又有随机性。神经网络在处理信息的整体性和模糊性方面主要依赖于混沌,即在确定性方程描述的动力学系统中表现其非确定性行为(随机性)。BP神经网络算法作为人工神经网络算法中应用最广泛、最成熟的算法,具有信号前向传递,误差反向传递的特点[19];WAVE相较前向的神经网络,其基元、整个结构依据小波分析理论确定,可避免结构设计的盲目性,具有更强的学习能力,精度更高[20];GRNN具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性,很适合于解决非线性函数的逼近问题[15]。
3.1 参数设置
本研究选取南咀站1956年1月至2005年12月平均流量数据作为神经网络输出训练样本集,选取安乡、石龟山站1956年1月至2005年12月平均流量、水位数据作为神经网络输入训练样本集;神经网络测试样本集为各站点2006年1月至2008年12月数据。
具体参数设置如下。
a)BP:采用4×125×1网络结构,迭代次数100次,学习率0.1,目标0.000 04,节点传递函数为tansig函数,训练函数为trainlm函数,网络学习函数为learngdm。
b)GRNN:采用交叉验证的方式寻求径向基函数的扩展速度。
c)WAVE:采用4×6×1网络结构,迭代次数100次,权值参数学习率为0.01、0.001。
3.2 评价方法
为考察算法预测的有效性和精确度,选取4项误差作为评价指标,分别为均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(ARE)、决定系数(R2)。
4 结果与分析
4.1 水位、流量特征分析
安乡、石龟山、南咀站水位、流量长时间序列情况见图1,图1a、1b中各站点水位、流量均随时间波动,由于安乡、石龟山站点均位于南咀站上游,南咀站流量年际间的波动与石龟山、安乡站水位、流量波动存在一定相似性。从图1c、1d可以看出年际间石龟山、安乡的流量、水位均呈下降趋势,变化量分别为68.634 m3/s、0.365 m,153.916 m3/s、0.273 m,南咀流量变化呈下降趋势,变化量为70.756 m3/s。其中安乡站流量、石龟山站水位年际间变化最为显著;从图1e、1f可以看出,南咀站年内最丰月份流量与最枯月份流量间差异随时间增大而增大,其1969年年内最枯月份流量与最丰月份流量相差6 423 m3/s,1999年年内最枯月份与最丰月份相差8 007 m3/s,此外,1990年以前年内最枯与最丰流量差值大于多年平均差值10 %的为18次,而1990年以后的19 a内有13 a南咀站年内最枯月份与最丰月份流量差值大于多年平均差值的10 %。安乡、石龟山站年内最丰月份流量与最枯月份流量间差异随时间增大而减小。这主要因为安乡、石龟山站位于南咀站上游,尤其安乡站位于松滋东支,随着长江三峡水库“清水下泄”模式运行导致整个长江主河道下切,松滋河口门位置不断抬高,洪水时期长江分流至松滋河水量减小,枯水期考虑生态问题长江下泄量增大使得松滋河流量维持在一定水平。石龟山站位于澧水洪道,但也受松滋河东支影响。安乡、石龟山水位年内最高水位与最低水位间的差异随年份增加而增大,且变化幅度分别为0.008 8、0.035 2 m/a。
4.2 EMD分解
南咀站作为安乡、石龟山下游站点,其水位、流量波动受石龟山站、安乡站以及区间来水影响较大,为探求各影响因素对于南咀站月平均流量作用,本文对南咀站月平均流量长时间序列进行EMD分解,得到1组不同尺度的分量及趋势项,见图2。月平均流量IMF分量的计算周期及贡献率见表1。各IMF分量包含不同周期震荡变化信息。从图2中可以看出分量IMF2是月平均流量原信号中振幅最大、能量最高的分量,且对月平均流量的波动贡献最大(73.238 %),除IMF1之外,随分量级数增大,振幅减小,能量较小,周期增大(表1)。从趋势项中可以看出南咀站的月平均流量呈现先减小后增大再减小的趋势,一定程度上与图1b南咀站的年际变化吻合。

a)各站点月平均流量序列

b)各站点月平均水位序列图1各站点水位、流量序列

d)各站点年平均水位序列
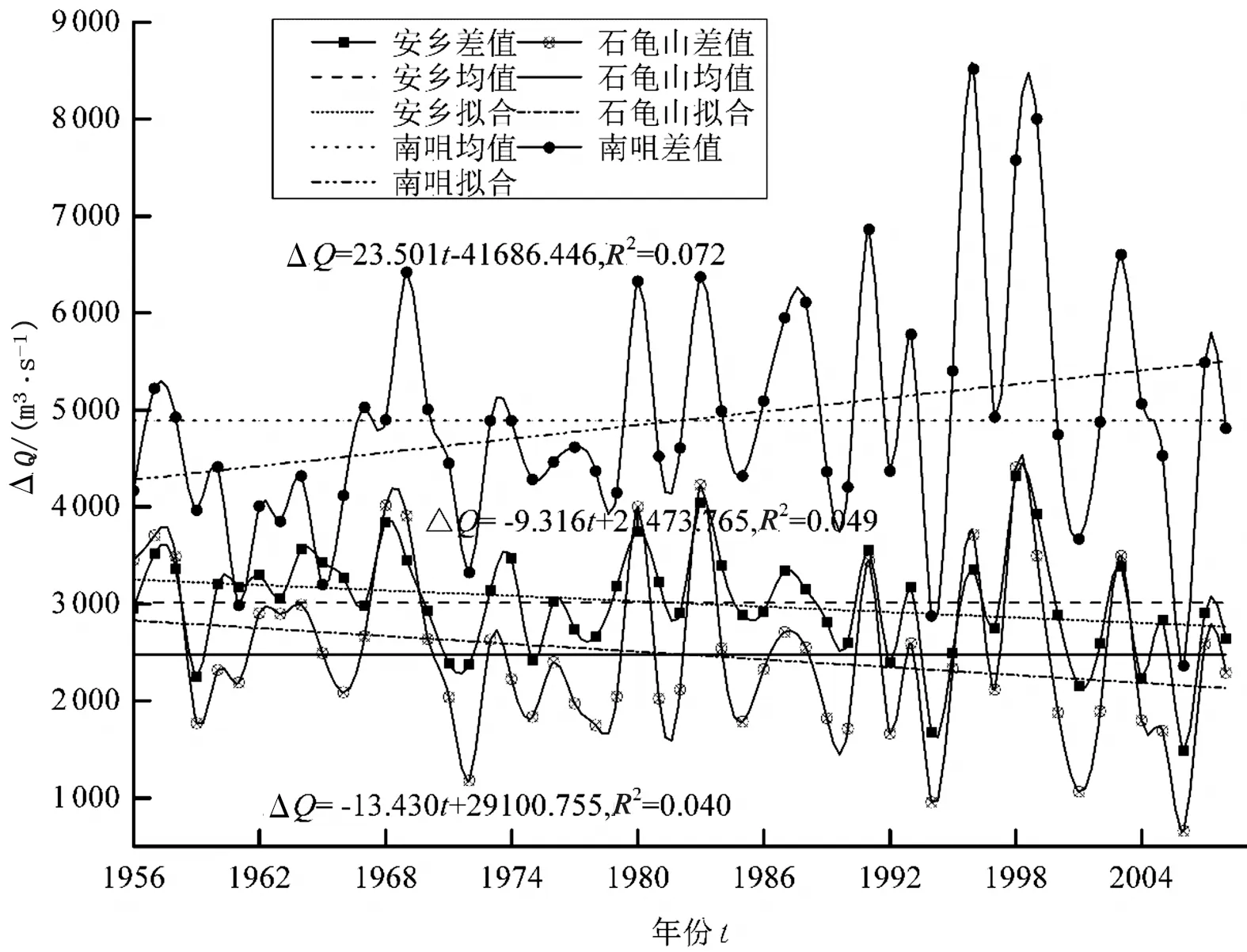
e)各站点年内流量差值序列

f)各站点年内水位差值序列注:Qa、Za、Qs、Zs、Qn分别为安乡站月平均流量、水位、石龟山站月平均流量、水位、南咀站月平均流量续图1各站点水位、流量序列

图2 南咀站流量序列EMD分解
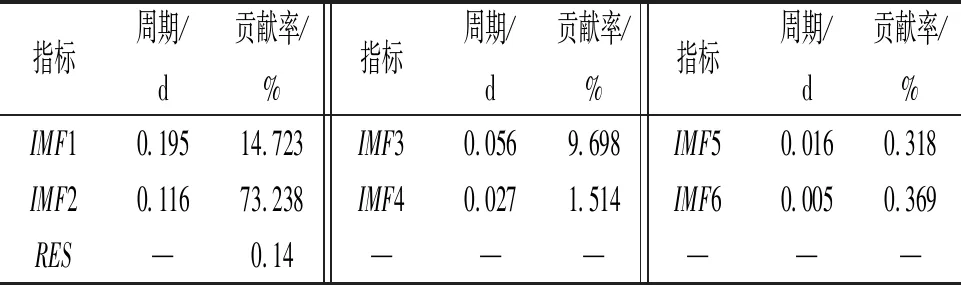
表1 南咀站EMD分解各IMF分量计算周期及贡献率
4.3 相关性分析
基于上述各站点月平均流量、水位原始信号分析可知,南咀站月平均流量与安乡、石龟山水位、流量存在一定关系,为量化其相关关系,并给予南咀站月平均流量IMF分量一定的物理意义,将各IMF分量与安乡、石龟山水位、流量进行相关性分析,见表2。
由表2可以看出,南咀站原始信号、IMF1—3分量与安乡、石龟山站的水位、流量间呈极显著的正相关关系;趋势项与安乡站流量、石龟山站水位呈极显著负相关关系,与安乡站水位呈负相关,但不显著,与石龟山站流量呈显著负相关关系。且相关系数绝对值:Zs>Qa>Qs>Za。这可能因为当南咀站出口南洞庭湖水位较低时,石龟山、安乡站水位抬升、流量加大会形成一定水位差,导致南咀站出流量加大;而当南洞庭湖水位比较高时,由于南咀站一侧为赤山第四纪红色黏土,质地黏重难以冲刷,另一侧为堤垸导致出流能力有限,遇荆南三口、澧水来水较大时,受南洞庭湖以及荆南三口、澧水间相互顶托作用导致石龟山、安乡站水位、流量不断抬升,南咀站流量变化不大现象出现。同时,随着长江三峡水库及上游梯级运用,南咀站流量变化由主要受安乡站所在的松虎洪道来水情况的影响向澧水、松虎洪道共同作用转化,以1956—1992、1992—2008年年平均流量来看,安乡站流量由129 6.577 m3/s减小为927.688 m3/s,石龟山站仅由879.590 m3/s减小至758.375 m3/s,南咀站流量由2 108.281 m3/s减至1 886.125 m3/s,即安乡站对南咀站流量贡献率由61.810%衰减至49.185%,石龟山站对南咀站流量贡献率由41.931%减至36.153%。此外,在三峡水库以“清水下泄”方式运用以来有研究表明整个长江中下游河道均处在冲刷的状态,导致河床底部高程降低,河道内水面降低,但河槽内蓄积的水量并未减小,即河道断面的流量仍有可能呈现增大的趋势。而与流经安乡站的松虎河相比,流经石龟山站的澧水河道较宽,相同水位落差下,石龟山站带来的流量变化大,同时,相同变幅条件下,水位抬升较流量增大对于泄流本身影响更大。

表2 各IMF分量与各站点流量、水位相关性
注:**为0.01显著水平下,*为0.05显著水平下
4.4 预测比较
根据南咀站流量数据EMD分解,本文设置3种模式:①安乡、石龟山站水位、流量数据作为输入数据,南咀站流量分解数据IMF1—7、Res作为输出数据(IMF-7);②安乡、石龟山站水位、流量数据作为输入数据,南咀站流量分解数据IMF1—3、Res作为输出数据(IMF-4);③安乡、石龟山站水位、流量数据作为输入数据,南咀站流量数据作为输出数据(Factor)。并结合GRNN、BP、WAVE3种神经网络算法估算南咀站月平均流量,见图3。
从图3中可以看出,与观测值相比,3种算法估算值除GRNN、BP算法、IMF-4模式下部分点大于观测值,其他点均偏小。从预测效果来看,Factor模式下,GRNN算法除相对误差13.860%>11.170%(BP),其他指标均优于BP算法,优于小波神经网络算法;IMF-7模式下,GRNN算法除均方根误差363.546 m3/s>329.229 m3/s(WAVE),其他指标均优于小波神经网络算法,优于BP算法;IMF-4模式下,GRNN算法优于WAVE、BP算法,而小波神经网络除决定系数R20.875>0.867(BP),其他BP算法均优于小波神经网络算法;GRNN算法估算径流时,Factor模式下平均绝对误差、均方根误差、平均相对误差、决定系数分别为140.218 m3/s、182.469 m3/s、13.860%、0.986,优于IMF-4模式和IMF-7模式,且IMF-4模式优于IMF-7模式。而BP、WAVE算法估算径流时,全输入模式优于IMF-7输入模式,IMF-7输入模式优于IMF-4输入模式。
同时,从图3中,可以看出在南咀站径流出现极大值时,神经网络算法的模拟效果不佳,一方面可能因为出现较大洪水时,上下游水库调度、蓄滞洪区运用等人类活动干预使得原有径流长序列数据一致性破坏,神经网络训练集与验证集从数据结构存在一定差异;另一方面,随着自然、人类活动的共同作用,导致大气环流、局部气候发生变化,局部地区极端天气出现,使得径流序列随机性更加复杂。此外,神经网络算法进行时间序列预测时理想条件需要输出值有界的同时还要有相当多均匀分布的已知样本,但自然界中完全均匀分布的现象不存在。

a)GRNN

b)BP

c)WAVE图3 基于神经网络估算南咀站流量对比

表3 南咀站月平均流量估算评价指标
注:MAE、RMSE单位为m3/s;ARE单位为%
5 结论
本文通过EMD方法对南咀站月平均径流量进行分解,结合相关性分析分离出与输入因子相关的IMF分量,引入BP、GRNN、WAVE算法估算、重构南咀站月平均流量序列,经对比分析得到以下初步结论。
a)南咀站月平均径流量EMD分解中,IMF2分量能量最高、振幅最大,贡献率最大(73.238%),分量IMF3—6随分量级数增大,振幅减小,能量较小,周期增大。
b)南咀站月平均流量IMF分量与安乡、石龟山站月平均水位流量相关性分析发现,分量IMF1—3与安乡、石龟山站水位流量呈极显著正相关关系,趋势项与石龟山站月平均水位、安乡站月平均流量呈极显著负相关关系,与石龟山站月平均流量显著负相关。
c)GRNN、BP、WAVE算法估算南咀站月平均流量表明,同一模式,GRNN算法均优于BP算法(Factor模式下除相对误差外)、小波神经网络算法(IMF-7模式下除均方根误差外);同一算法,Factor模式均优于IMF-7模式,IMF-7模式优于IMF-4模式(除GRNN算法外)。
EMD分解在神经网络进行径流估算中还涉及其他一些问题,以南咀站为例,分量IMF4—6与安乡、南咀站水位、流量间并无显著相关关系,后续研究中一方面需考虑藕池河中支水位、水文站点以及南咀站附近控制性雨量站对于南咀站月平均流量的影响;另一方面需从人类活动对于径流影响方面入手,开展径流还原计算,通过自然、人类活动两方面叠加考虑径流预测。

