Fully Diagonalized Spectral Methods for Solving Neumann Boundary Value Problems

LIU Fujun(刘付军),LU Jing(卢静)

( 1.School of Science,Henan University of Engineering,Zhengzhou 451191,China;2.School of Computer Science,Henan University of Engineering,Zhengzhou 451191,China)

Abstract: The fully diagonalized spectral methods using generalized Laguerre functions are proposed for the second-order elliptic problems with Neumann boundary conditions on the half line.Some Fourier-like Sobolev orthogonal basis functions are constructed for the diagonalized Laguerre spectral methods of Neumann boundary value problems.Numerical experiments demonstrate the effectiveness and the spectral accuracy.

Key words: Diagonalized Laguerre spectral method; Generalized Laguerre function;Second-order elliptic problem; Neumann boundary value condition

1.Introduction

During the past forty years,significant progress has been made in the research on Laguerre spectral methods for solving differential equations on unbounded domains[1−4,9,12,14,18].Usually,one often considers certain problems with Dirichlet boundary conditions[5−6,8,11].However,it is also interesting and important to consider various problems with Neumann boundary conditions.In a standard variational formulation,this kind of boundary condition is commonly imposed in a natural way.Unfortunately,this approach usually leads to a full stiffness matrix.

Recently,[16]proposed a Laguerre spectral method for solving Neumann boundary value problems,which gets a tridiagonal matrix instead of the full stiffness matrix encountered in the classical variational formulation of such problems.However,in many cases,people still pay more attention to obtain a set of Fourier-like basis functions for a fully diagonalized algebraic system[13].Based on this reason,the main objective of this paper is to construct some new Fourier-like Sobolev orthogonal basis functions and further develop the fully diagonalized Laguerre spectral methods.We shall focus on the second-order elliptic Neumann boundary value problems on the half line.Starting with(see (2.3)),we construct the Fourier-like basis functions and propose the fully diagonalized spectral methods for the elliptic problems mentioned above.We also present some numerical results to demonstrate the effectiveness and accuracy of the proposed diagonalized Laguerre spectral methods.

The remainder of the paper is organized as follows.In Section 2,we first make conventions on the frequently used notation,and then introduce the generalized Laguerre functions with arbitrary indexα.In Section 3,we propose the fully diagonalized Laguerre spectral methods and the implementation of algorithms for the second-order elliptic Neumann boundary value problems on the half line.We also present some numerical results.

2.Generalized Laguerre Functions

LetΛ=(0,∞)andϖ(x)be a weight function which is not necessary inL1(Λ).We define

with the following inner product and norm,

with the following semi-norm and norm,

In cases where no confusion arises,ϖmay be dropped from the notation wheneverϖ(x)≡1.Specifically,we shall use the weight functionsωα=ωα(x)=xαandω=ω(x)=xin the subsequent sections.

We denote by R the collection of real numbers,by N0and Z−the collections of nonnegative and negative integers,respectively.Further,let Pkbe the space of polynomials of degree≤k.

Letℵ:=Z−∪(−1,+∞).We also define the characteristic functionsχnforn ∈N0,

For short we writeχ(α)=χ0(α).

It is well known that,forα>−1,the classical Laguerre polynomialsLαk(x),k=0,1,...,admit an explicit representation (see [15]):

where we use the Pochhammer symbol (a)n=a(a+1)...(a+n −1) for anya ∈R andn ∈N0.

The classical Laguerre polynomials can be extended to cases with anyα ∈R and the same representation as(2.1),which are referred to as the generalized Laguerre polynomials[10].Obviously,the generalized Laguerre polynomialsLαk(x),k=0,1,...,constitute a complete basis for the linear space of real polynomials as well,since degLαk=kfor allk ≥0.

The generalized Laguerre functionsare defined by[7]

According to [7],for anyα ∈Z−,we have

which means thatx=0 is a zero of(x) with the multiplicity−α,i.e.,

Hereafter,we use the convention thatwheneverk ∈Z−.

The generalized Laguerre functions satisfy the following recurrence relations[7]:

Lemma 2.1For anyk ∈N0,we have

The generalized Laguerre functions are eigenfunctions of the following singular Sturm-Liouville differential operators[7]:

Lemma 2.2For anyn ∈N0,we have

whereλαk,nsatisfies the following recurrence relation,

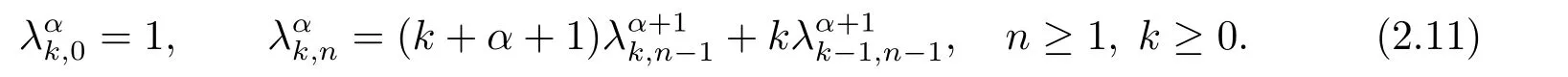
For anyn ∈N0,α ∈R andβ >0,we define the bilinear form on

It is obvious thataαn,β(·,·) is an inner product onHωnα+n(Λ) ifα+n>−1.

Lemma 2.3[7]The generalized Laguerre functionsforα ∈ℵare mutually orthogonal with respect to the weight functionωα,

where the positive numbersγαk,nsatisfy the recurrence relation

under the convention thatγαk,n=0 wheneverk ∈Z−.

To propose the fully diagonalized spectral methods,we also need the following results which can be derived directly from (2.6),(2.7) and (2.13).

Lemma 2.4(i) The mass matrixis symmetric pentadiagonal,i.e.,

and

and

Lemma 2.5According to (2.16) and (2.19),for anyγ >0,we have

3.Fully Diagonalized Spectral Methods for Solving Neumann Boundary Value Problems

Consider the second order elliptic problems with Neumann boundary conditions:

A weak formulation of (3.1) is to findu ∈H10(Λ)={u ∈H1(Λ),u′(0)=0},such that

Clearly,iff ∈(H10(Λ))′,then by Lax-Milgram lemma,(3.2) admits a unique solution.

Let

The generalized Laguerre spectral scheme for (3.1) is to finduN∈X0,βN,such that

To propose a fully diagonal approximation scheme for (3.2) ,we need to construct new basis functions{Sβk}2≤k≤Nwhich are mutually orthogonal with respect to the Sobolev inner productAγ(·,·).

For an efficient implementation,it is very important to select appropriate basis functions.Certainly,one can choose the generalized Laguerre functionsas the basis functions for the scheme (3.3).However,as pointed out in (2.22),are pentadiagonal with respect to the Sobolev inner productAγ(·,·).For the scheme (3.3),it is more appropriate to consider the basis functions that are mutually orthogonal with respect to the Sobolev inner productAγ(·,·).To this end,we shall use diagonalization techniques to obtain new Laguerre-Sobolev basis functions{Sβk(x)}2≤k≤NinX0,βN,which are mutually orthogonal with respect to the inner productAγ(·,·).

Theorem 3.1Assume thatSβk(x)∈X0,βN,2≤k ≤N,whose leading coefficient is the same as the Laguerre function(x),satisfies the orthogonality:

Then we have

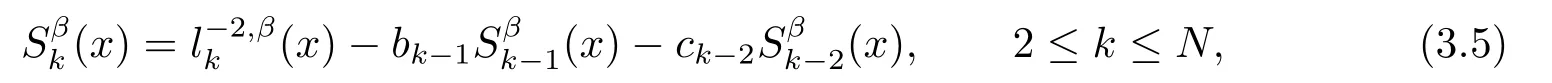
wherebk=ck=0,Sβk(x)=0 for anyk ≤1 and

ProofSetWe first check thatdm=0 for 2≤m ≤k −3.In fact,by (3.4) we get that for any 2≤j ≤k −3,

This,along with (2.22),gives thatAγ(l−2,βk,Sβj)=0,2≤j ≤k −3.Hence,we havedj=0 for 2≤j ≤k −3.This leads to (3.5).

Next,by (2.22),we derive that for 2≤k ≤N,

On the other hand,by (3.4) and (3.5) we deduce

A combination of (3.7) and (3.8) yields

This leads to the first formula of (3.6).Moreover,for any 2≤k ≤N,we have

Hence,we use a similar argument as in (3.7) and (3.8) to obtain

This leads to the second formula of (3.6).Further,owing to

we use a similar argument as in (3.7) and (3.8) to obtain

This leads to the third formula of (3.6).

It is clear that

In the following,we denote bythe orthonormal basis functions,such that

Fig.3.1 L2-errors

Fig.3.2 H1-errors

Fig.3.3 L2-errors

Fig.3.4 H1-errors

u(x)=xe−xsinx,which is exponential decay.In Figs.3.1 and 3.2,we plot the discreteL2-andH1-errors vs.Nwith various values ofβin a semi-log scale.Clearly,the approximate solutions converge at exponential rates.We also see that for fixedN,the scheme withβ=3 produces better numerical results than those withβ=1,2.However,the choice of the optimal scaling factorβfor a given differential equation is still an open problem.Generally speaking,the choice ofβdepends on the asymptotic behavior of solutions.

u(x)=x2(1+x)−h,h >52,which is algeb√raic decay.In Figs.3.3 and 3.4,we plot the log10of the discreteL2- andH1- errors vs.Clearly,the approximate solutions converge at algebraic rates.We also see that for fixedN,the scheme withh=6 produces better numerical results than those withh=4,5.