基于三角模糊数层次分析的医疗设备事后维修决策研究

沈一奇，郑彩仙，郑焜

浙江大学医学院附属儿童医院 医疗设备科，浙江 杭州 310003

引言

医疗设备的维修方式主要包括事前维修和事后维修。事前维修是在故障发生前预先按照要求对设备进行维修，旨在降低对安全和环境有直接危害的故障发生率。事前维修在故障发生前进行，其优点显而易见。但事前维修只能降低故障发生率，无法避免所有的故障，当医疗设备发生故障已成既定事实，事后维修不可避免。在做事后维修方式的决策时，一方面，决策方案大致分为院内自行维修、第三方维修、厂家维修，这些方案各有利弊[1]；另一方面，做出决策时，需要考虑的因素很多，比如安全性、维修性、经济性等。因此，医疗设备事后维修方式的决策属于多属性决策问题。

层次分析法（Analytic Hierarchy Process，AHP）是应用最广泛的多属性决策方法之一，它可以将复杂的问题构建为树形结构，决策者通过对同一层次的节点进行两两比较做出决断，整个决策过程清晰可行。实践证明在医疗设备维修管理领域运用层次分析法进行决策，可以避免盲目性和主观性[2-4]。

但是传统的层次分析法在构造判断矩阵时，取某一数值作为标度来衡量专家做出的定性判断[5]。由于数值是确定的，专家的判断可能是模糊的，所以这一过程在量化专家判断的同时，也造成了一部分信息的丢失。另一方面，由于各个因素本身存在着模糊性，专家的判断有时是一个范围，使用确定数值来表征这样的判断是不合适的。为了最大限度地表征专家的模糊判断，可以使用模糊数代替数值作为衡量的尺度[6-7]。三角模糊数在设备维修方面的应用已取得一定成果，但在医疗设备维修方面则少[8-10]。本文运用三角模糊数和层次分析法进行维修建模分析，希望对医疗设备事后维修决策做出探索。

1 三角模糊数的基本概念及运算

1.1 三角模糊数的基本概念

三角模糊数是最简单的模糊数，其应用也最广。其定义是：设A为实数域R上的一个模糊集，若λ ∈ [0, 1]，Aλ是R中有限闭区间，则称A为R上的一个模糊数。设A∈F(R)，F(R)为R上的全体模糊集，则A为模糊数当且仅当R中存在有限闭区间[a, b]使得：① 在[a, b]上，μA(x)≡1；② 在[-∞, a]中，μA(x)为右连续的增函数，且0≤μA(x)＜1；③ 在[b, +∞]中，μA(x)为左连续的减函数，且 0 ≤ μA(x))＜1。

那么，若A的隶属函数μA(x)：R→[0,1]可表示为：

式中 l＜m＜u且l, m, u∈R。

特别的：

即可称A为三角模糊数，记为 (l, m, u)。l和u分别为A的下限和上限，m为A的中值，也就是最可能值。三角模糊数的函数示意图，如图1所示。

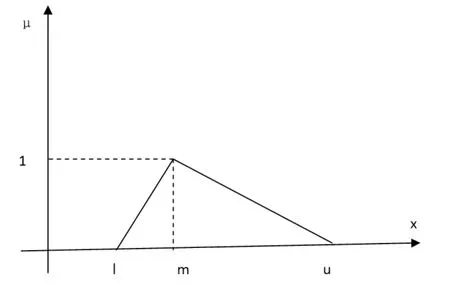
图1 三角模糊数函数示意图

1.2 三角模糊数的基本运算

基本运算定义如下，假设存在三角模糊数，M1=（l1,m1, u1）和 M2=（l2, m2, u2）

1.3 三角模糊数的排序

三角模糊数的排序又称为三角模糊数的去模糊化，其方法较多，本文根据文献[11]利用可能度来比较模糊数的大小,进而排序。其公式为

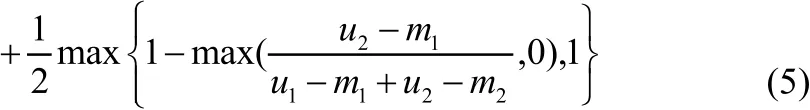
P(M1≥M2)表示M1大于等于M2的可能度。P(M1≥ M2)+P(M2≥ M1)=1。P(M1≥ M2)大 于 0.5时，M1＞M2；(M1≥ M2)小于 0.5 时，M1＜M2；P(M1≥ M2)等于 0.5时，M1=M2。

2 实例应用

某型B超发生故障，初步判断是电源部分没有输出。有三种维修方式可供选择：原厂维修，第三方维修和自行维修。原厂维修更换新的电源模块，报价10万。由于申请配件、物流等原因，承诺5个工作日完成维修工作；第三方维修更换电源模块，但模块为拆机件，报价5万，承诺4个工作日完成维修工作；自行维修由院内资深工程师进行元件级维修，维修费用控制在1000元以内，估计15个工作日完成维修工作。

类似实例在维修工作中非常常见。原厂维修更换模块，维修效率高，维修价格也高；第三方维修，可能进行元件级维修，可能更改电路，可能更换模块，更换的模块可能是拆机件，可能非原厂生产，方法不一而足，总体来讲维修效率和效果比不上原厂维修，而比院内自行维修要好一些，维修价格也在二者之间；院内自行维修则是维修效率较低，且可能投入时间和精力后，最终无法找到故障点，即使找到故障点，最终还面临无配件的风险，但是一旦成功，维修价格则非常低[12-13]。

面对这种问题，我们有时会只关心维修价格，有时会只关心维修时间，这样做出的决策会很盲目。如果我们同时考虑价格和时间，又会有些无所适从。因此需要进行维修建模来帮助我们做出决策。

2.1 构建层次结构模型

综合考虑影响决策的所有因素，归纳起来分成三个准则：安全性，经济性，维修性，构成主准则集U={Ui，i=1,2,3}。子准则集U1={人员安全U11，设备安全U12，信息安全U13}，U2={停机损失U21，维修价格U22，设备剩余价值U23}，U3={备件供应情况U31，维修技术条件U32，维修效果U33}。需要说明的几点是：

（1）安全性主要是指维修过程中的安全，而非设备维修后使用过程中的安全。人员安全是指维修对院内人员的安全影响。设备安全是指设备在维修过程中故障扩大的风险以及对其他联合使用的设备造成损害的风险。信息安全是指在维修过程中或维修后，医疗信息出现泄露的风险。

（2）停机损失实际取决于维修时间、设备日收益和设备可替代程度。设备剩余价值可以根据该设备修复后预期使用年数做判断。

三种维修方案构成评价集V={原厂维修V1，第三方维修V2，自行维修V3}，最终的决策结果为评价集中的元素。构成的层次结构如图2。

图2 维修方式决策层级结构图

2.2 构造各层级的所有矩阵并计算权重

请专家按照模糊度量的尺度分别对准则层、子准则层和方案层的因素进行两两比较评判，由此获得所有的判断矩阵。对于模糊的评判，要求专家优先使用三角模糊数的形式评判，即给出上下限和主值。不能给出三角模糊数完整形式的评判，根据表1转换为三角模糊数。对于精确的评判，同样用三角模糊数表示。

表1 模糊度量尺度

设判断矩阵为A=[aij]，用求和法公式计算局部权重：

子准则的全局权重由子准则的局部权重与所属主准则的局部权重相乘得到。其结果见表2～3。

表2 主准则层对目标层之间的判断矩阵及其权重

所有的子准则的全局权重组成权重向量，记为S。则S= [(0.0307, 0.0728, 0.1796), (0.0212, 0.0497, 0.1286),(0.0092, 0.0203, 0.0490), (0.0122, 0.0296, 0.0730), (0.1097,0.2718, 0.6676), (0.0498, 0.1271, 0.3246), (0.0157, 0.0576,0.2551), (0.0303, 0.0726, 0.1903), (0.1327, 0.2983, 0.7540)]。

相同的方法，可以计算得到评价元素对子准则层的判断矩阵和局部权重。三个评价元素对应人员安全子准则的判断矩阵和局部权重，见表4。评价元素对应其余8个子准则的判断矩阵也都可以分别计算相应的局部权重，这些局部权重值可以组成一个3×9的评价矩阵，记为R。

表3 子准则层对准则层的判断矩阵及其权重

表4 方案层对子准则人员安全U11的判断矩阵及其权重

评价集的综合权重向量为：W=S×R=[w1, w2,w3]=[(0.0947, 0.3666, 1.6087), (0.0592, 0.2318, 1.1154), (0.1199,0.4015, 1.4865)]。

画出三个权重值的图像示意图，见图3。

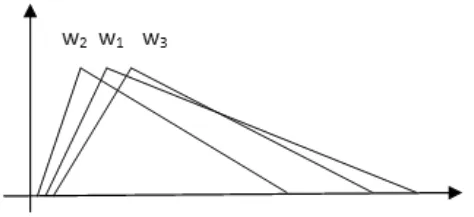
图3 权重值图像示意图

2.3 模糊数排序

对三个综合权重进行模糊数排序，所得结果为：P(w1≥ w2)=0.6697；P(w1≥ w3)=0.4823；P(w2≥ w3)=0.3045。所以 w3＞w1＞w2。

2.4 结果

根据计算结果，最终选择自行维修的方式。实际故障原因为三极管击穿，导致保险管烧断，更换三极管和保险管排除故障，维修花费时间13 d，维修费用100元以内。

3 讨论

维修建模及优化技术是运筹学和可靠性工程学的重要分支，致力于综合衡量维修相关的各个因素，给出最佳的评价。与其他维修模型，如以可靠性为中心的维修相比，维修建模更侧重于对系统以及维修工作进行定量的描述和分析[14]。维修建模和优化在医疗设备维修中的各类应用研究已有不少[3,10,15]，但是针对事后维修的应用研究却不多。事后维修作为目前医疗设备主要的维修方式[16]，其理论研究是相对不足的。对于事后维修，临床工程师往往“头痛医头，脚痛医脚”，疲于应付，缺乏科学严谨的管理决策。这种目前事后维修研究大量集中在探寻特定设备的特定故障的解决方法，缺乏系统性的理论研究可见一斑。事实上事后维修的成败，关键看维修的效率。熟悉设备故障固然是提高维修效率的一种手段，维修建模和优化技术的应用则显然是提高维修效率更具普遍性的方法。