舰艇磁性检测中矢量磁传感器的姿态校正

(中国人民解放军 91336部队，河北 秦皇岛 066000)

0 引言

水面舰艇的船体主要由钢铁建造，在地磁场作用下会被磁化从而产生舰艇磁场，为获得准确的舰艇磁场信息，一般通过将矢量磁传感器安放于舰艇周围以进行舰艇磁性检测。舰艇磁性检测一般分为静态磁性检测与动态磁性检测[1-3]，如大平面布阵测量、测量环检测法和移动式检测等方式，其中大平面布阵法通过在海底布置大规模的磁传感器阵列以获得固定深度下的舰艇磁场测量值；测量环检测法将磁传感器环形排列，当舰艇行驶在测量环内可获得舰艇空间包络面上的磁场信息；移动式检测法通过将少数磁传感器在舰艇下方等距水平排列，具有快速布置、方便使用的特点。在上述方式中为保证磁测量数据的准确性，都要求磁传感器具有较高的安装精度，即磁传感器坐标系与设定的主坐标系一致，然而在海洋环境背景下矢量磁传感器受到冲击、震动时姿态会发生变化，从而导致磁场测量的准确度下降，且由于磁传感器已密封安装，其姿态难以通过物理方式校正，因此需要定期对磁传感器进行姿态校正，以保证舰艇磁性检测的精度。

目前舰艇磁性检测中对于磁传感器的姿态校正一般不考虑垂直方向，而多注重水平方向的姿态变化[4-5]，如文献[5]通过对舰艇磁场进行建模，以模型拟合误差为适应度采用遗传算法得出了较高精度的水平偏转角。实际中矢量磁传感器受外部影响会发生倾斜、偏转，将与设定坐标系间产生3个不同方向的姿态角，为贴近实际本文对3个姿态角综合考虑，提出了一种针对水下矢量磁传感器姿态校正的新方法，通过在倾斜磁传感器附近放置一标准磁传感器，以标准测量值为依据采用APO混合算法对倾斜测量值求解，得出了磁传感器在x、y、z三个方向上的姿态偏转角，并可对磁测量数据进行修正，获得准确的磁场测量信息，从而提高了舰艇磁性检测中矢量磁传感器的测量精度。本文通过仿真证明了该方法的正确性，并在船模实验中进行了具体分析与验证。

1 舰艇磁性检测模型

在舰艇磁性检测中矢量磁传感器固定封装于海底固定点处，舰艇在海面上沿直线匀速行驶。在仿真验证中通过单椭球体加磁偶极子阵列混合模型进行模拟舰艇磁场，根据混合模型的计算公式可获得磁传感器所在位置的舰艇磁场强度，将其作为标准磁传感器的测量真值，并通过姿态变换方程可得出倾斜磁传感器的测量值，对此模拟测量数据进行可反推计算出姿态偏转角，将磁测量校正结果与磁场真值比较以验证此方法的正确性。

1.1 舰艇磁场模型

采用单椭球体与磁偶极子阵列混合模型模拟舰艇磁场，具体如图1所示。椭球体用来模拟舰艇的主磁场，其长半轴a=L/2(L为舰艇纵向长度)，短半轴b=B/2(B为舰艇横向长度)，椭球心与舰艇中心重合。磁偶极子阵列用来模拟舰艇的局部磁场，N个磁偶极子在舰艇长轴上均匀分布(N取奇数)，相邻两磁偶极子间隔为c=L/(N-1)，则第i个磁偶极子坐标表达为[(i-(N+1)/2)c,0,0]。

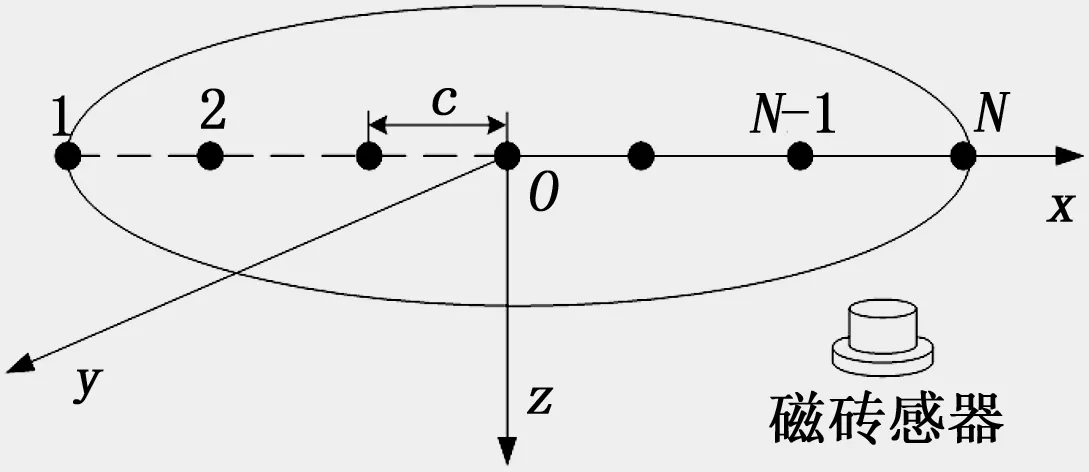
图1 舰艇磁场模型

设定椭球体磁矩为M0=[Mx0,My0,Mz0]，第i个磁偶极子的磁矩为Mi=[Mxi,Myi,Mzi]，则tj时刻磁传感器位置处的舰艇磁场大小为Hj=[Hxj,Hyj,Hzj][6]

(1)

上式可简写为H=FM，其中H=[H1,H2,…,Hm]T，M=[M0,M1,…,MN]T，F中元素与模型中磁偶极子及椭球相对测量点的距离有关，具体根据舰艇运动时的位置可计算得出，由此根据式(1)可模拟出舰艇在磁传感器所在位置的磁场值。

1.2 三分量磁传感器测量模型

首先在实验前测量地磁背景场，假定标准磁传感器三轴两两相互正交且没有测量误差，当传感器坐标系与大地坐标系一致时，磁传感器的测量值即为舰艇磁场磁场与地磁背景场的叠加值，将地磁背景去除后可得舰艇磁场的标准测量值H。当磁传感器倾斜时，其所在坐标系与大地坐标系在x、y、z方向分别产生α、β、γ三个姿态角，将此倾斜条件下磁传感器测量值中的地磁背景场去除可得倾斜后测量值B，则测量值B与舰艇磁场H的关系[7]可描述为:

B=AH

(2)

其中:A为大地坐标系与磁传感器坐标系之间的转换矩阵，简称姿态角矩阵：

A=

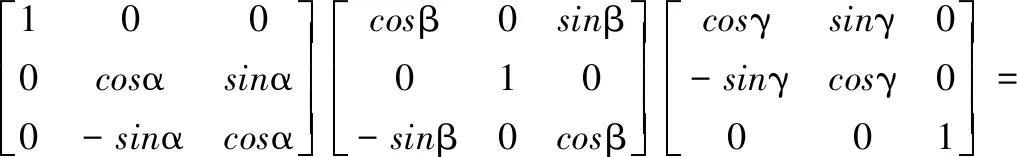
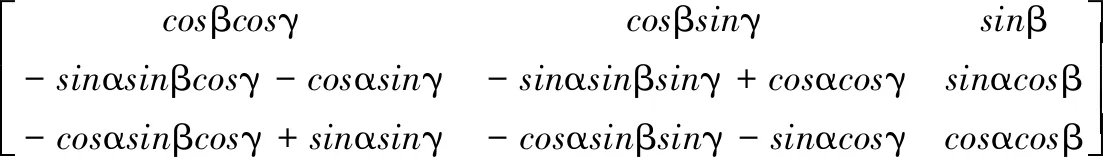
(3)

由式(3)分析可知A的模为1，且实际中姿态角α、β、γ都较小，A中元素aij在[-1,1]范围内。由式(2)可知磁传感器的姿态校正归结于A矩阵的求解，当A已知后根据磁测量值B反推可得出真实的舰艇磁场值H。

2 求解方法

假定磁传感器1放置海底且姿态倾斜，紧靠此磁传感器位置放置一姿态标准且无测量误差的磁传感器2，则认为磁传感器2测量值为真实值。当舰艇在海面航行通过时，磁传感器1、2分别获得测量值B与H，则根据式(2)由B与H可求解得出A矩阵，在求解过程中定义目标函数为：

(4)

式(4)中,n为测量点数，共获得n组测量数据，以姿态角矩阵A中元素作为位置求解参数，当求解结果逼近真实值时，由式(4)可知目标函数F趋近于0，当F取得最小值时则认为得到最优求解值，并由此可对倾斜测量值进行修正得出无倾斜条件下的磁场测量真值。为在较少求解次数下获得较高的求解准确度，本文采用蚁群粒子群混合优化算法(简称APO)求解A矩阵，其算法流程如图2所示。

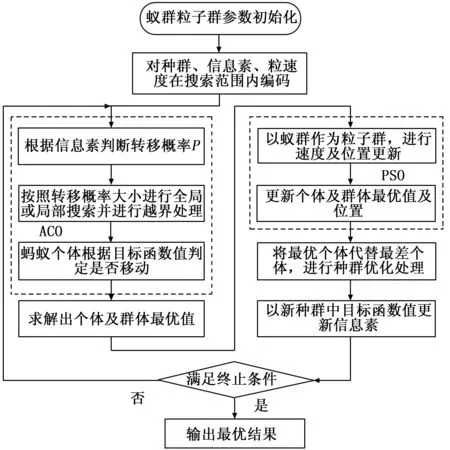
图2 APO算法流程图

APO算法中具有蚁群算法(ACO)与粒子群算法(PSO)的重要步骤，由于ACO中蚂蚁在觅食路径上释放信息素以传递信息从而相互协作，具有较强的鲁棒性和较好的搜索能力，但求解中计算量大且收敛速度偏慢，且易陷入局部最优；粒子群算法(PSO)模拟鸟类的捕食行为，具有并行处理和计算效率高的特点，但易产生早熟收敛现象。APO通过将两种算法融合，充分发挥优势并克服各自缺点，其主要思想是以蚁群算法为主体框架，以待求解参数作为蚂蚁个体并使其具有粒子特性，采用ACO中的搜索步骤，并在搜索过程中个体进行越界处理，同时将ACO中蚂蚁信息素与PSO中目标函数结合，采用PSO进行路径选择[8-9]，满足终止条件后得到最终优化结果，具体步骤如下：

1)初始化。设定蚂蚁个数m，每个蚂蚁xi含有9位(xi∈[xmin, "xmax])，分别代表A矩阵中9个元素，同时蚂蚁也为PSO中的粒子，即蚂蚁也具有粒子性。设定蚂蚁初值，蚂蚁xi的信息素τi=C-F，(C为一较大正值)，τi也是PSO中的适应度函数fitness，这样就将目标函数最小值转化为求信息素的最大值。

2)转移概率。蚂蚁根据信息素大小判断是否转移，则第i只蚂蚁的转移概率为：

(5)

3)蚂蚁更新。蚂蚁根据转移概率进行局部搜索或全局搜索：

(6)

式(6)中,λ=1/t，t为迭代次数，p0为固定值。当蚂蚁搜索后，根据适应度函数求取每个蚂蚁的历史最优值Pbest及群体最优值Gbest，以便于采用PSO进一步搜索。

4)粒子的速度及位置更新。将上述蚂蚁个体作为粒子，根据粒子历史及群体最优值更新速度与位置，则粒子在第d维的具体变化公式为：

(7)

式(7)中,ω为惯性权重系数，取较大值时有利于全局搜索，取较小值有利于局部搜索，ω变化公式为:

ω(t)=ωstart-(ωstart-ωend)·(t/T)

(8)

其中:T为最大迭代次数，ωstart与ωend分别为ω取值范围的边界值。

5)优化替代。对更新后的新个体进行适应度值排列，将其中适应度较小的个体替换成具有最大适应度的个体，以此加快全局收敛速度。

6)信息素更新。当所有蚂蚁完成以此循环后，信息素进行更新

τi(t+1)=(1-ρ)τi(t)+fitness(t)

(9)

式(9)中,fitness(t)为经过PSO更新后的适应度函数，ρ为信息素衰减系数。

3 实验结果及分析

3.1 磁测量值模拟

首先对磁传感器测量数据进行模拟计算，设定混合模型中磁偶极子相邻间隔为5 m，磁椭球体长轴为15 m，短轴为5 m，舰艇在海平面上以1 m/s匀速前进。磁传感器位置为[80,50,20](m)，每隔3秒记录一次，测量前可预先测量地磁场并当舰艇通过时将其从测量值中去除，则磁测量值中只含有舰艇磁场。

将椭球与磁偶极子的磁矩代入式(1)可计算得出磁传感器2的标准磁场测量值H。设定磁传感器1的姿态角分别为α=3°，β=5°，γ=2°，由式(2)得出磁测量值B，为显示磁传感器的倾斜对测量带来的影响，将B与H在三分量上进行比较，定义ΔBx、ΔBy、ΔBz分别为B与H在三分量上的差值，其具体结果如图3所示。

图3 B与H对比曲线

由图3可知，即使磁传感器倾斜含有较小的姿态角，也会导致磁测量值在三分量上产生较大幅度的测量误差，其在三分量上的最大波动幅度达到了近百纳特，而实际中经过消磁处理后的舰艇磁场本身的绝对值大小通常在百纳特级，这必然会对舰艇磁性检测的精度产生不利影响，因此说明有必要修正因磁传感器姿态倾斜引起的测量误差。

3.2 仿真及分析

为符合实际测量条件，对B与H分别加入幅度为5nT的白噪声，以模拟磁传感器本身的测量随机误差。本文采用APO对磁测量值B求解姿态角矩阵A，对此方法进行仿真验证，其算法参数初始化设定如下：

1)种群中个体数目n=50，初始化中xi中元素的范围为[-1,1]，最大迭代次数为150。

2)ACO算法模块中参数：转移概率p0=0.2，信息素衰减系数ρ=0.8，信息素中常数C=105。

3)PSO算法模块中参数：c1=c2=1.49445，r1与r2为[0,1]区间的随机数，ωstart=0.9，ωend=0.4，粒子速度v的范围为[-0.5,0.5]。

本文以目标函数F作为评价标准，当F越小时说明求解结果越精确。在每一次迭代搜索中记录适应度值fitness，将其与常数C相减得F的变化值。为表明APO算法的优越性，将其与ACO与PSO的求解结果一同比较，F的变化曲线及A矩阵求解结果如下所示，其中Re为求解值与真值间的相对误差：

图4中显示经多次迭代计算后APO求解精度最高，随着迭代次数的增加目标函数F迅速减小，经历较少代数搜索得到全局最优值。表1中APO计算得到的姿态角转换矩阵A中元素aij精度在1%以内，与设定值基本一致，其精度相比ACO与PSO要高许多，同时PSO相比ACO具有较好的求解效果，PSO经多次迭代计算目标函数F达到最小值，

图4 目标函数变化曲线

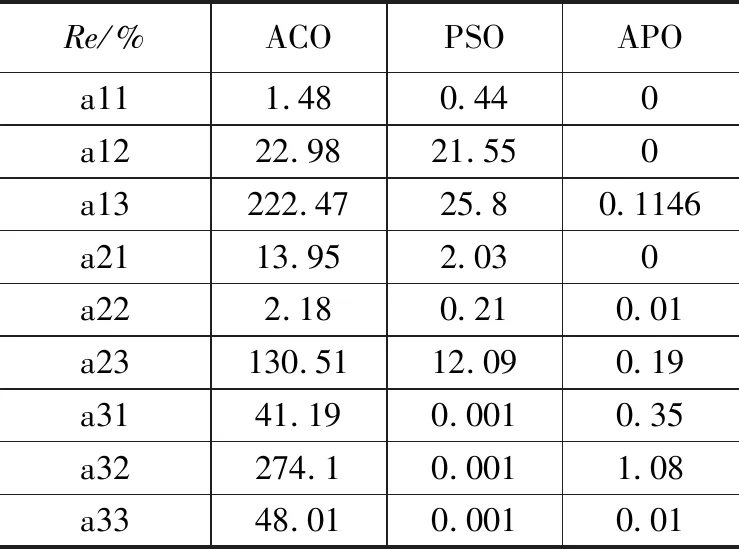
Re/%ACOPSOAPOa111.480.440a1222.9821.550a13222.4725.80.1146a2113.952.030a222.180.210.01a23130.5112.090.19a3141.190.0010.35a32274.10.0011.08a3348.010.0010.01

但在个别元素的求解上还不够精确。经上述比较可知，3种算法中APO求解效果精度最高，其次为PSO，而ACO的求解不太理想，同时也说明采用APO进行磁传感器姿态校正的方法是可行的，在磁场测量中将计算得到的A矩阵与磁传感器1测量值B代入式(2)即可得到准确的舰艇磁场测量值H。

3.3 实验验证

为证明此方法在模拟实际环境下的正确性及有效性，采用船模实验进行验证，其实验示意图如图5所示。

图5 实验示意图

实验中两个磁传感器位于船模正下方沿y方向紧密放置，1号磁传感器姿态倾斜，其测量值作为需校正值B，2号磁传感器x轴指向磁北，经水平校正后无姿态误差，测量值作为标准值B，此实验具体步骤如下：

1)采样点在无磁轨道上均匀分布，共25个，其相互间距为25 cm。磁传感器1、2位于12号采样点下方，沿z轴垂直方向距船模1 m。

2)采用两种型号船模进行实验验证，分别定义为Ι型与Π型。船模水平放置无倾斜，船首指向地磁北，依次推进船模到1～25号采样点。移动Ι型船模时得到磁传感器1、2的测量值B1与H1，移动Π型船模得到测量值B2与H2。

根据测量值B1与H1采用APO算法求解1号磁传感器的姿态角矩阵A，将A与H2代入式(2)得校正后的磁场值Bc=AH2。若矩阵A求解正确，则校正值Bc应与Π型船模的测量标准值B2相同，因此定义校正前误差ΔB=B2-H2，校正后误差ΔBc=B2-Bc，当ΔBc趋近于0说明校正效果越好，ΔB与ΔBc在三分量上的对比结果如下

表2 校正结果对比

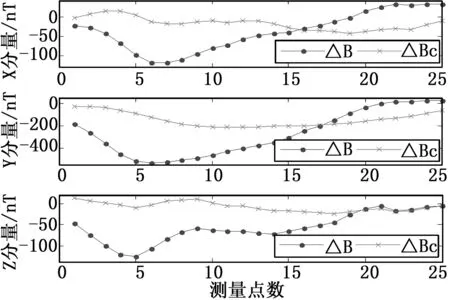
图6 姿态校正前后ΔBc对比

由上述结果可知，校正后ΔBc相比校正前ΔB在三分量上的变化幅度及均方差均降了近70%，说明姿态矩阵A的求解结果较为正确，校正后1号磁传感器测量精度有了较大改善。在表1中ΔBc在x、z分量上绝对值最大不超50 nT，但在y分量上绝对值较大，究其原因具体分析如下：

1)2号磁传感器作为标准磁传感器，测量时应没有正交、标度、零位等固有测量误差，但限于实验室测量条件并没有对2号磁传感器进行固有误差的校正，将其作为标准测量值H并不完全准确，这会对姿态矩阵A的算带来不利影响。

2)1号与2号磁传感器紧密放置，两者具有体积故产生一定距离，为保证2号磁传感器的测量值能够作为标准测量值H，应采用小体积磁传感器以保证两者间距离足够小，从而最大限度减小体积因素的影响。

3)实验中传感器相距船模较近，而实际舰艇磁性检测中两传感器轴心间距相比传感器到舰艇的距离小很多，因此实际中应使磁传感器距离舰艇满足一定的限定要求，从而可将此不利影响忽略。

综上述分析，欲提高姿态校正后的测量精度需采用小体积三分量磁传感器，且需对其进行正交、标度、零位等固有误差的校正以保证求解的准确性。

4 结束语

舰艇磁性检测是获取舰艇磁场的重要手段，实际中由于磁传感器姿态倾斜从而导致无法获得准确的磁测量值。将标准姿态且无误差的磁传感器置于倾斜磁传感器处，依据标准测量值采用APO算法对倾斜传感器测量值求解可得出其姿态角矩阵，进而计算获得准确的舰艇磁场值。本文对该方法进行了仿真与船模实验，验证了方法的准确性，同时指出实际中应采用小体积且无固有误差的三分量磁传感器以保证求解的精度，若能将磁传感器的固有误差与姿态误差一同校正，可使测量结果进一步精确，这也是该方法今后需要改进的方向。