基于软土常规物理参数的压缩模量预测研究

张 鹤

（中铁第五勘察设计院集团有限公司 北京 102600）

1 引言

压缩模量（Es）是判断土的压缩性和计算地基压缩变形量的重要指标之一。受土体的压缩性影响，在计算地基沉降时，必须考虑地基土在上部荷载作用下的应力分布情况对土体压缩过程的影响。在铁路工程当中，一般通过地质勘察取原状土样，并测定其在侧限与轴向排水条件下的变形与压力的关系、孔隙比与压力的关系或变形与时间的关系来计算土的压缩模量等参数［1］。然而在实际工作中，土层尤其是软土地层受其自身结构和沉积等原因的限制，在由钻探现场至试验室的钻探、取样、运输、贮存等一系列过程中极易受到扰动，室内压缩试验得到的土体压缩模量Es值与实际原位值存在偏差［2］。如何获得土体准确的压缩模量成为工程师们的研究重点之一。

针对此问题，前人已经从不同角度入手做了一些研究，如基于CPTU测试的压缩模量预测［3］、粉质黏土标贯击数与压缩模量的线性拟合［4］和基于e-lg p曲线Harris函数快速获取土体压缩模量的方法［5］等研究均卓有成效。回窥土体本身，土的物理参数与压缩模量之间必然存在联系，一直以来学者们都在尝试用土常规物理参数评价其压缩性指标并获得二者之间的一些线性拟合关系。相比实验室法而言，土的常规物理参数使用扰动样即可获得，在一定程度上突破了必须依靠原状样才能测得压缩模量的限制。鉴于土常规物理参数与压缩模量之间的灰色数学关系难以用简单的线性关系解释，使用人工神经网络进行预测体现出了优势。近年来人工神经网络技术应用广泛，在铁路路基沉降及变形预测［6］、砂土液化概率判别［7］、基坑水平位移［8］等工程领域也取得了较好的效果，体现其对工程领域复杂隐函数求解的有效性。因此，本文将以获取原状试样相对困难的软土为研究对象，以MLP和RBF神经网络为研究方法，进行软土常规物理参数对压缩模量的预测研究。

2 建立预测模型的可行性

2．1 建立“软土物理参数—压缩模量”预测模型的理论基础

土具有固液气三相性，其物理性质及其在空间内所处的初始条件控制着土体的力学特性。前人为了能够通过土体的一些基本物理参数反映其压缩性，对土体的物理指标和压缩指数Cc之间的线性关系进行了研究，表1罗列了部分适用于软土的关系式［9］。

从表1中可以看出，土体的液限、塑性指数、天然含水率等常规物理指标与土体压缩指数Cc之间具有一定的线性关系。其中基于液限wL与Cc之间线性相关建立的关系式最多，其深层次原因是液限wL为衡量土体吸附水分能力的重要指标［10］，在一定程度上控制着土的压缩性指数。然而，有些学者认为基于液限建立的压缩系数表达式存在不可靠之处［11］，即使液限相同，但诸如塑限等参数不同的土体仍然表现出不同的压缩性。此外，由于土体的压缩性不仅取决于土体的固有性质，同时也取决于初始条件，土体的初始孔隙比e0同样控制着其压缩性质［12］。

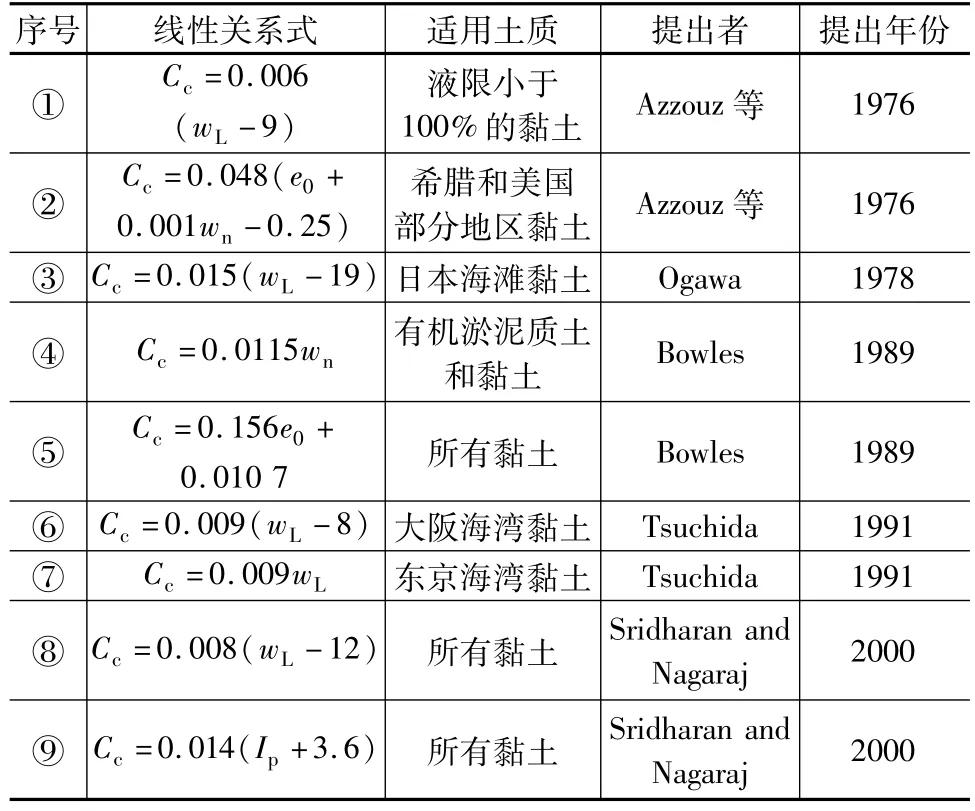
表1 土体的物理指标和压缩指数C c之间的线性关系

综上所述，土的各项常规物理参数均与土的压缩性质之间存在一定联系，单独使用某个参数或二至三个参数进行线性拟合不足以准确预测土体的压缩模量。而人工神经网络则可以综合各物理参数的特性并表达出其与压缩模量之间的模糊关系，具有良好的自适应性、自组织性和很强的自学习、联想、容错、抗干扰能力，可以做到对土体压缩模量的综合预测。以上为本文基于土常规物理参数建立“软土物理参数—压缩模量”神经网络预测模型提供了理论基础和实用基础。

2．2 多层感知器（MLP）

多层感知机（MLP，Multilayer Perceptron）作为一个传统的神经网络使用反向传播算法，可以被用来拟合复杂的函数或用于深层学习。其中隐含层可以是单层或者多层，已有研究表明，含有单隐含层的3层神经网络在理论上可以任意精度逼近任意的连续函数，因此在多数问题的研究中可采用3层BP神经网络［13］。其网络结构如图1所示。

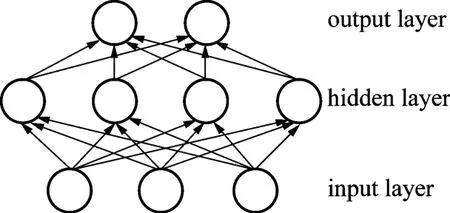
图1 MLP神经网络结构示意

作为一种前向结构的人工神经网络，MLP可以被看作是一个有向图，由多个节点层组成，每一层全连接到下一层。除了输入节点，每个节点都是一个带有非线性激活函数的神经元。

假设输入层用向量X表示，则隐藏层的输出就是 f（W（1）x+b（1））。W（1）为权重，b（1）为偏置，函数 f常选用sigmoid函数或者tanh函数：

隐藏层到输出层为softmax回归，故输出层表达式为 softmax（W（2）x1+b（2）），其中 x1表示隐藏层的输出 f（W（1）x+b（1））。因此，MLP整个模型的公式可以总结为：

其中函数G是softmax。

因此，MLP所有的参数就是各个层之间的连接权重以及偏置，包括 W（1）、b（1）、W（2）、b（2）。MLP一般采用梯度下降法（SGD）来解决求解最佳参数的最优化问题，此过程涉及到代价函数、规则化（Regularization）、学习速率（learning rat-e）、梯度计算等参数选择。首先随机初始化所有参数，通过反复迭代运算，不断地计算梯度和更新参数，直到满足误差条件后停止，从而得到理想的神经网络模型。

2．3 径向基函数（RBF）

RBF网络模型（Radial Basis Function）在逼近能力、分类能力和学习速度等方面均较优。RBF网络由三层组成，其结构图与MLP一致。输入层节点只是将输入信号传递到隐藏层，隐藏层节点通常是由基函数构成，输出层节点通常是简单的线性函数。隐藏层节点中的基函数（核函数）对输入信号在局部产生影响，即当输入信号靠近核函数的中央范围时，隐藏层节点将产生较大地输出。这种网络具有局部逼近能力。

隐藏层基函数通常采用高斯核函数：

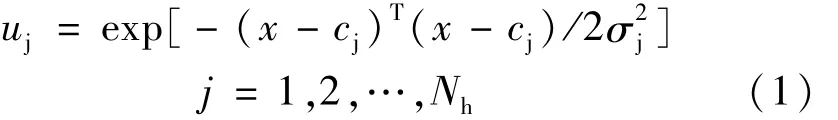
式（1）中uj是第 j个隐藏层节点的输出；X＝（x1，x2，…xn）T是输入样本；Cj是高斯核函数的中心值；σj是标准化常数；Nh是隐藏层节点数。由式（1）可知，节点的输出范围在0和1之间，且输入样本愈靠近节点的中心值，输出值愈大。高斯基函数具有形式简单、径向对称、光滑性好及存在任意阶导数等优点。RBF网络模型的输出为隐藏层节点输出的线性组合：

式（2）中 W＝（wi1，xi2，…xiNh，-θ）T；U＝（u1，u2，…uNh，1）T。RBF网络模型的学习过程分为两个阶段。第一阶段，根据所有的输入样本决定隐藏层各节点的高斯核函数的中心值Cj和标准化常数σj；第二阶段，在决定了隐藏层的参数后，根据样本，利用最小二乘原则，求出输出层的权值Wi。有时在完成第二阶段的学习后，再根据样本信号，同时校正隐藏层和输出层的参数，以进一步提高网络的精度。

3 数据源与神经元选择

本文所用的样本来源于作者全程参与的某铁路定测阶段地质勘察工作所取得的高质量样品。工程所在地位于浙江省沿海冲海积平原区，软土的取样质量一直以来难以监管，随之而来的就是室内试验所得到的压缩模量数据不准确。

为尝试解决此问题并使预测研究具有代表性，本文筛选了27个钻孔中90件高质量淤泥及淤泥质土试样的土常规物理参数及压缩模量数据作为研究数据源。所选样品的钻探及取样过程满足《铁路工程地质钻探规程》（TB 10014-2012）［14］中的要求，试验过程依据《铁路工程土工试验规程》（TB 10102-2010）。湿密度采用环刀法测定、含水率采用烘干法测定、颗粒密度采用量瓶法测定、界限含水率采用液塑限联合测定法测定、压缩系数及压缩模量采用标准固结试验法测定。各样品准备的数据类型及各参数之间的换算关系分别见表2及表3。

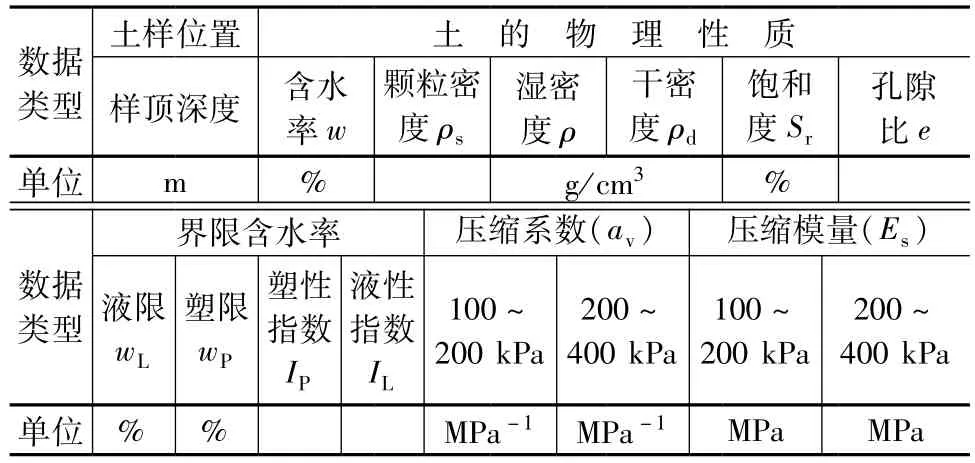
表2 样本数据类型

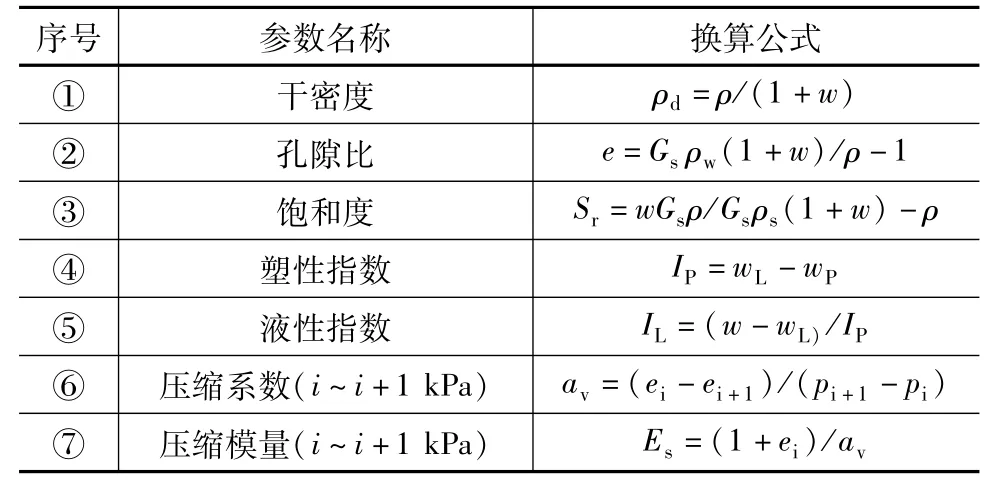
表3 部分物理参数换算公式

前文所准备的数据中，样顶深度用来描述土样所处的空间位置，代表土体所处的初始条件，需列作神经元之一；由表2及表3可以看出，含水率、颗粒密度、湿密度、液限、塑限为实测值，应列作神经元；塑性指数、液性指数可由塑限及液限线性表示，可舍去；孔隙比、干密度和饱和度虽也为计算值，但可以更为直观地描述土的特性，故应在神经元之列；压缩系数与压缩模量均反映土体压缩性，但压缩模量在各项检算工作中使用起来更为方便直接，且Es1-2在评价土压缩性时为大多数学者及工程人员所接受。为避免二次计算扩大不必要的误差，故仅将压缩模量置于输出端。

综上，本次预测研究的输入端为样顶深度、含水率、颗粒密度、湿密度、干密度、饱和度、孔隙比、液限和塑限等9个影响因素；输出端为压缩模量1个数值且Es1-2及Es2-4分别计算。

4 模型试算及误差分析

4．1 模型试算

各模型的神经元按前文所确定的参数类型选取，将90个样本数据按7∶3的比例随机分配得到63个训练样本和27个测试样本。为了得到更为准确的参数预测模型，本次预测将对不同神经网络（MLP和RBF）的不同激活函数所产生的模型进行对比。各模型培训参数如表4所示。

为直观地对比各模型的预测效果，对Es1-2和Es2-4的预测结果采用堆积图的方式成图展示。如图2所示，各模型对于Es1-2的预测结果在趋势上与原值相当，均有较好的预测效果。但对于Es2-4的预测结果，各模型的预测结果有较大差距，预测曲线变化趋势与原值曲线基本相当，但整体效果相较于Es1-2的预测结果有差距。

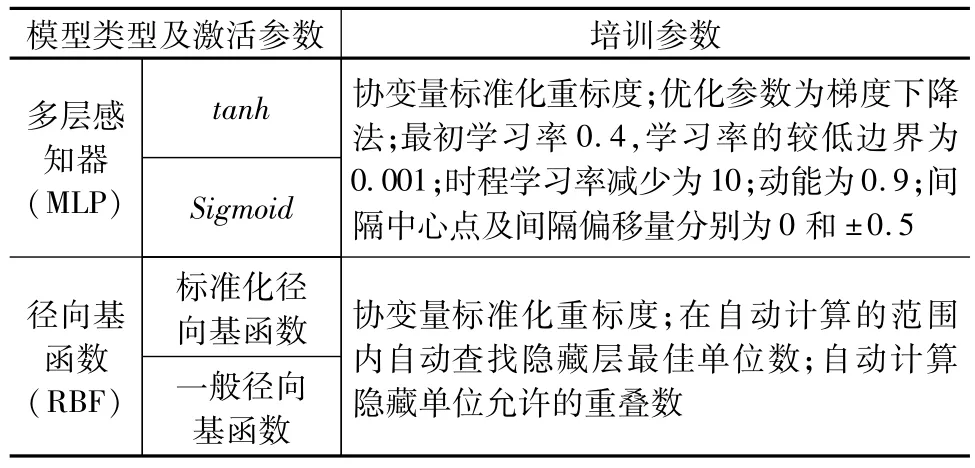
表4 模型培训参数选择

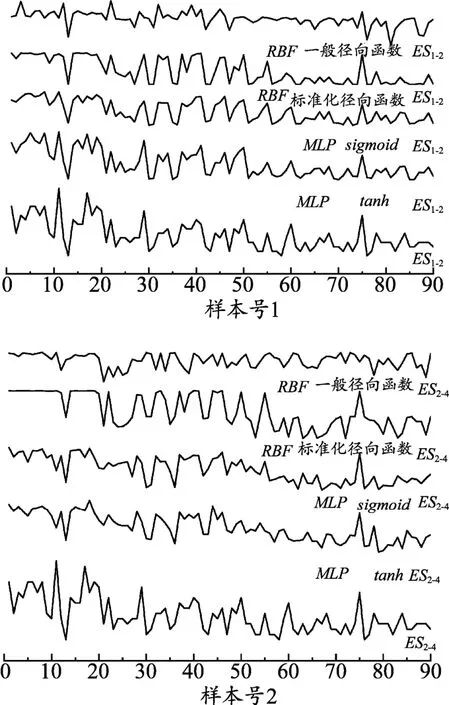
图2 模型预测结果对比

4．2 误差分析

对比模型的预测输出值和实测值只能定性地区分模型的预测效果，为进一步对比各模型的预测精度，分别计算各预测模型对各预测参数的相对误差并做可视化对比，具体如图3及图4所示。由图3可见，在对Es1-2值进行预测时，以双曲正切tanh函数为激活函数的MLP神经网络的相对误差曲线位于图幅最下方，且数值波动范围相对较小；而其他几种模型的预测值相对误差曲线分离性偏弱，数值波动范围相对较大。由图4可见，在对Es2-4值进行预测时，各模型的相对误差均较大，但以标准径向基函数为隐藏层激活函数的RBF神经网络的相对误差曲线数值波动范围相对较小，可以在一定程度上代表其优越性。

图3 Es1-2模型预测的相对误差

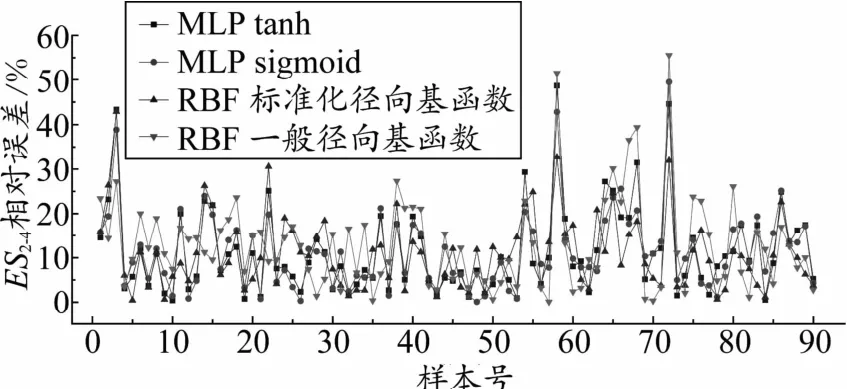
图4 Es2-4模型预测的相对误差

为更加对各模型的预测精度有定量描述，分别计算各类模型预测的平均相对误差（MRE）和均方根误差（RMSE）列于表5；为方便对比这两项模型预测精度评价指标，根据表5的数据制作图形进行对比分析，如图5所示。

表5 模型预测的平均相对误差（MRE）和均方根误差（RMSE）

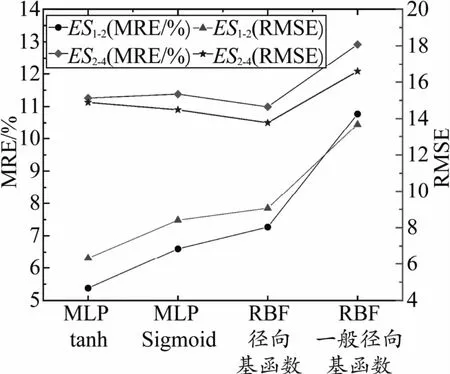
图5 模型的MRE和RMSE对比

由图表可清晰看出以双曲正切tanh函数为激活函数的MLP神经网络模型对Es1-2值进行预测时平均相对误差在5%左右，均方根误差在6%左右；以标准径向基函数为隐藏层激活函数的RBF神经网络模型对Es2-4值进行预测时平均相对误差小于11%，均方根误差小于14%。

由此可见，模型对于Es1-2值的预测精度优于Es2-4值。以上研究可以说明，在优选模型的基础上，在一定误差的允许范围内，基于神经网络可以依靠软土的常规物理参数对压缩模量进行预测。

5 结论与讨论

5．1 结论

（1）基于前人研究分析了土的常规物理参数与土体压缩模量之间的必然联系，明确了基于人工神经网络建立“软土物理参数—压缩模量”预测模型的理论基础，且神经网络模型可以综合各物理参数的特性并表达出其与压缩模量之间的模糊关系，从而做到对土体压缩模量的综合预测。

（2）以27个钻孔中90件高质量淤泥及淤泥质土试样的土常规物理参数及压缩模量数据作为研究数据源，基于MLP和RBF神经网络分别以tanh、sigmoid和标准径向基函数及一般径向基函数为激发函数建立不同的神经网络，通过优选得到了对于Es1-2预测值和Es2-4预测值的MRE分别在5%左右和11%以下，及RMSE分别在6%左右和14%以下预测模型。因此，在一定误差的允许范围内，基于神经网络可以依靠软土的常规物理参数对压缩模量进行预测且存在继续优化的空间。

5．2 模型优化方向探讨

RBF网络相比于其他的前馈神经网络，具有学习速率快的特点，其输出结果是隐含层单元输出的线性加权求和。径向基函数的扩展系数对于网络提高模型的回归预测精度非常关键，通常取默认值1.0，实际上应当针对不同的应用问题选取最优值。扩展系数的取值既不能过大也不能过小。取值过小，径向基神经元不能够对输入向量所覆盖的区间产生全覆盖响应；但也不要求取值过大到所有的径向基神经元被全覆盖，只要保证部分的径向基神经元可以对输入信息所覆盖的区间产生响应即可。扩展系数值越大，通常得到的输出结果越光滑，但是过大的话将会给数值计算带来困难。

综上分析，在设计径向基神经网络时，需要在一定的范围内对扩展系数进行遍历寻优，寻找到最恰当的值构建网络模型。在今后的压缩模量预测研究中，有待针对土体的物理力学性质设计一种优化算法对径向基的扩展系数进行优选，建立基于混合算法的网络模型，以使模型的预测精度更高，模型的鲁棒性能越强。