基于改进PSO-BP神经网络的冰蓄冷空调冷负荷动态预测模型
杨熊,于军琪,郭晨露,华宇剑,赵安军
(西安建筑科技大学 a.信息与控制工程学院;b.陕西省新型城镇化与人居环境研究院,西安 710055)
随着中国社会经济的快速发展,能源短缺和环境恶化现象日益突出,沉重的能源负担已成为阻碍经济可持续发展的重要桎梏。其中,建筑能耗约占全社会总能耗的30%[1],在所有建筑中,大型公共建筑因其舒适度要求高、人流量大、空调系统运行时间长等原因,已成为建筑能耗中的“巨无霸”,其空调系统单位建筑面积能耗约为城镇建筑的5倍[2]。作为缓解这种紧张局面的一种有效方式,冰蓄冷空调系统利用水/冰相变潜能储存能量,使用夜间低价电制冰蓄冷,白天用电高峰融冰释冷,以满足建筑物的负荷需求,不仅对电网的电力负荷具有移峰填谷的作用,同时,也降低了用户空调系统的运行费用。合理匹配谷段及峰段电价时间内制冷机组供冷和蓄冰装置融冰供冷是冰蓄冷空调系统优化控制的核心问题,其中,准确的冷负荷动态预测数据更是冰蓄冷空调系统节能优化的首要因素。
当前,建筑冷负荷预测方法主要有回归分析法、仿真模拟法和机器学习法。回归分析法主要包括多元线性回归模型(MLR)[3]、自回归(AR)模型[4]。由于MLR模型在影响建筑冷负荷的多变量方面具有严重的非线性,因此,预测精度相对较低。AR模型输入变量仅为建筑冷负荷的历史数据,而没有考虑其他因素,预测精度也很难满足实际要求。常用的建筑冷负荷模拟软件有TRNSYS[5-6]、ESP-r[7-8]和EnergyPlus[9-10]等,其在冷负荷预测过程中软件程序效率较低,主要表现在:1)系统模型的建立需要花费较长的时间,并且模型也必须根据实际运行结果进行验证和完善,才能产生高精度的输出;2)由于模拟软件通常用于空调系统的前期设计阶段,因此,在系统运行阶段难以提供准确、实时的指导控制;3)建模过程中参数设置对建模人员的专业化、工程经验均要求高。综上所述,传统的仿真软件程序不适合用于实际的系统管理。随着人工智能AI(Artificial Intelligence)的快速发展,其中,BP(Back Propagation)神经网络以其突出的非线性映射、自适应、容错性强等特点,广泛地应用于建筑冷负荷的动态预测[11-15]。然而,BP神经网络具有局部最优、收敛速度慢、对训练数据依赖性大的缺陷,往往又阻碍了其在实际工程中的应用。多数研究者采用粒子群优化算法PSO(Particle Swarm Optimization)的全局搜索能力优化BP神经网络,极大地避免模型陷入局部最优的缺陷。然而,由于模型输入变量与输出变量相关性差、冗余度高导致的模型预测精度差的缺陷仍然没有得到良好解决[16-17]。
笔者在传统PSO-BP神经网络全变量预测模型的基础上,采用灰色关联度分析法对模型输入变量预处理,剔除相关性较低的因子,采用与输出结果关联度高的因子作为模型输入变量预测大型公共建筑冰蓄冷空调系统动态冷负荷。研究表明,该改进模型相对于传统PSO-BP神经网络全输入变量预测模型在预测精度、收敛速度方面均有较大的提高,满足工程实际应用需求。
1 大型公共建筑冷负荷动态预测模型
1.1 灰色关联度分析法
灰色关联度分析法是一种多因素统计分析方法,以各因素的样本数据为依据来描述输入因素对输出结果影响的强弱、大小和次序[18]。若输入变量与输出结果变化的趋势、速度基本一致,则它们之间的关联度较大;反之,关联度较小。该方法避免了由于输入变量不对称带来的损失,并且对数据要求较低,工作量较少,广泛用于数据预处理。
1.2 PSO-BP神经网络算法
PSO-BP神经网络将粒子群优化算法引入BP神经网络,利用PSO算法的全局搜索特性和BP算法快速局部搜索能力,达到良好的预测效果[19-21]。PSO-BP神经网络模型,将网络权值和阈值映射为种群粒子编码,以样本输出值与期望值之差的绝对值之和为粒子适应度函数,通过反复迭代,最终获得最优粒子,解码后得到BP神经网络全局最优权值和阈值。
2 基于改进PSO-BP神经网络的大型公共建筑冷负荷动态模型
2.1 实验数据来源与分析
实验数据来源于西安赛格国际购物中心,该建筑物高40.6 m,总建筑面积25 万m2,商业面积20 万m2,分为地下两层,地上八层,建筑空调面积18.76 万m2,夏季空调采用部分蓄冷的冰蓄冷空调系统。
冰蓄冷空调冷负荷预测训练样本的输入层节点通常为T时刻室外空气温度、湿度、太阳辐射强度、室外风速[22-25],考虑到太阳辐射、室外温度会导致建筑空调冷负荷存在严重的滞后现象,因此,在预测模型中还加入了T-1 h时刻室外空气温度、太阳辐射强度[26]。考虑到空调冷负荷的时间序列性,相关研究还加入了T-1 h时刻空调冷负荷、T-2 h时刻空调冷负荷、T-3 h时刻空调冷负荷以及T-24 h时刻空调冷负荷作为模型输入变量。输出层节点为T时刻空调预测冷负荷。
实验以6月、7月空调系统逐时冷负荷数据、室外干球温度数据、室外空气湿度以及太阳辐射强度等变量做为训练数据,采用8月份数据对模型进行验证分析,如图1所示。3个月的室外气象参数与空调冷负荷均具有强烈的关联性,3个月某日中空调冷负荷随着室外气象参数的变化发生相应的变化:室外温度、太阳辐射强度与空调冷负荷正相关,室外湿度与空调冷负荷负相关。
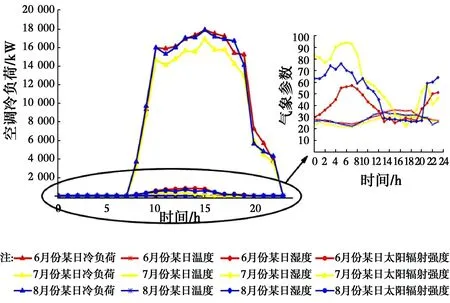
图1 6月、7月、8月空调冷负荷与室外气象参数曲线图Fig.1 Air-conditioning cooling load and outdoor meteorological parameters in June, July and
2.2 输入变量关联性分析
采用灰色关联度分析法,计算输入变量与输出结果间灰色关联度,具体步骤如下。
step1:采用式(1),建立相关指标的原始数据矩阵xi;
xi=(xi(0),xi(1),xi(2)...,xi(23))
(1)
式中:xi(0),xi(1),xi(2)...,xi(23)分别表示第i个变量在0:00—23:00时刻的值。
step2:采用式(2),建立初始化变化矩阵
xi(2)/xi(0),...xi(23)/xi(0))=
(2)
step3:采用式(3),求差序列Δoi(k);
(Δoi(0),Δoi(1),...,Δoi(23))
(3)
Step4:采用式(4)、式(5),计算关联系数ξoi(k)和灰色关联度γoi;
(4)
(5)
空调冷负荷动态预测模型各输入变量与T时刻空调冷负荷灰色关联度如表1。
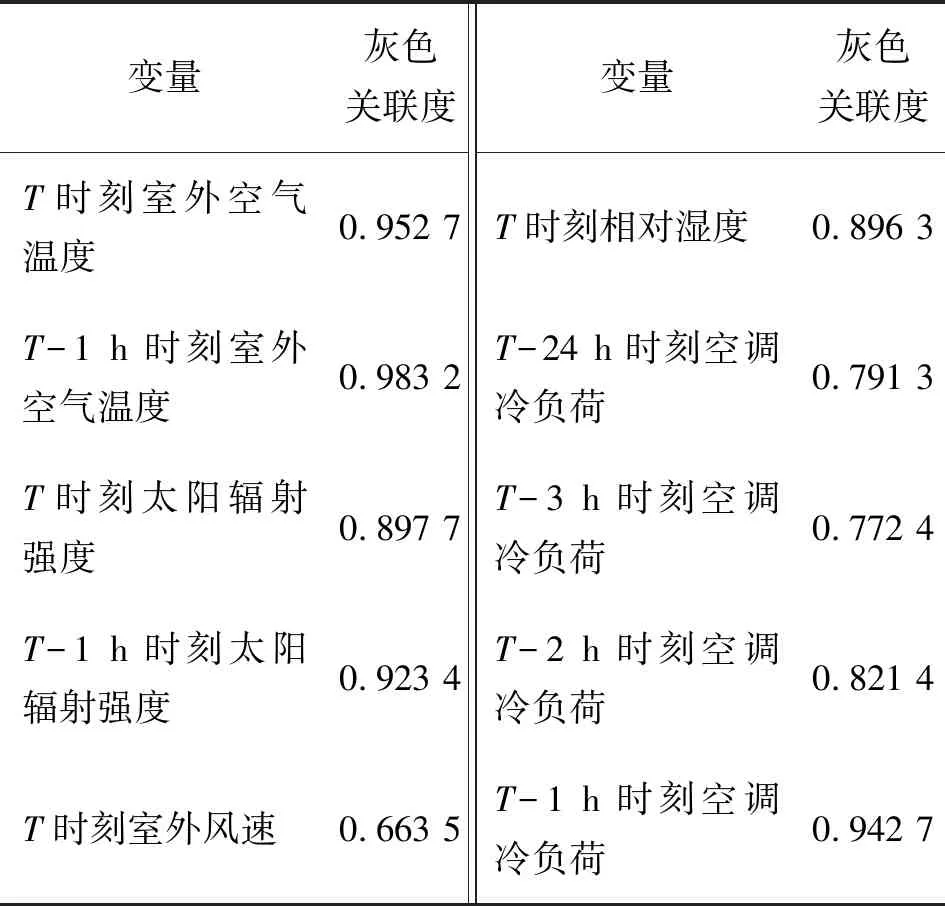
表1 各影响因子与T时刻空调冷负荷灰色关联度Table 1 The impact of various factors andT timeair conditioning cooling load gray correlation
由上述分析可知,T时刻室外风速与T时刻空调冷负荷关联度较小,关联度系数仅为0.663 5,这是由于多数大型公共建筑采用封闭式的外围护结构,没有与外界形成自然通风,室内形成相对封闭的环境,因此,室外风速对空调系统冷负荷的影响较小;T-24 h时刻空调冷负荷与T时刻空调冷负荷关联度为0.791 3,由于前一天与当天可能会存在较大的气象参数差异,因此,相同时刻的空调冷负荷就会存在较大差异;T-3 h时刻空调冷负荷、T-2 h时刻空调冷负荷相对于T-1 h时刻空调冷负荷与T时刻空调冷负荷关联度较低,为了降低仅由于历史冷负荷对T时刻冷负荷的耦合作用,仅采用关联度较高的T-1 h时刻空调冷负荷作为历史冷负荷影响T时刻预测冷负荷的关键因素;T时刻室外空气温度、湿度、太阳辐射强度与T时刻空调冷负荷表现出较高的关联性,这与多数大型公共建筑冷负荷影响因素研究的结论一致[4,7,11,15,27-28]。由于室外空气温度、太阳辐射强度对大型公共建筑空调冷负荷存在严重的滞后性,因此,T-1 h时刻室外空气温度、太阳辐射强度与T时刻空调冷负荷关联度也较高。
综上分析,确定T时刻室外空气温度、T-1 h时刻室外空气温度、T时刻室外空气湿度、T时刻太阳辐射强度、T-1 h时刻太阳辐射强度、T-1 h时刻空调冷负荷为影响T时刻空调冷负荷的关键因素。
2.3 基于PSO-BP神经网络模型进行大型公共建筑动态冷负荷预测
基于上述对预测模型输入变量的分析,实验采用3层BP神经网络结构,输入层神经元数为6,T时刻空调冷负荷数据为输出层,故输出层神经元数为1,隐含层因子数由经验式(6)得出为13。隐含层节点采用tansig转移函数,输出层节点采用purelin转移函数。
m=2n+1
(6)
式中:m为隐含层神经元个数;n为输入层神经元个数。
1)由于神经网络训练函数的活性范围为[0,1],采用式(7)离差标准化对输入数据进行处理。
(7)
2)初始化粒子群的规模,包括种群粒子个数N、粒子个体长度D、粒子的初始速度、位置。
试验中粒子数N取值为100,粒子个体长度D的计算式为
D=S1S2+S2S3+S2+S3
(8)
式中:S1、S2、S3分别为BP神经网络输入层因子数、隐含层因子数、输出层因子数。计算得D=105。
3)粒子适应度计算。以预测值和观测值的误差绝对值之和作为粒子适应度值F,计算公式为
(9)
式中:n为样本数;yi为样本i的观测值;Oi为样本i的预测值。
4)粒子适应度比较。比较规则为:
如果sse 如果sse 其中:sse是粒子的当前适应值;pbestfitness是粒子的个体最优适应值;gbestfitness是种群全局最优适应值;pbest是粒子个体最优值;gbest是种群全局最优值;xi为当前计算粒子。 5)粒子位置及速度的更新。采用式(10)、式(11)进行粒子速度及位置的更新。 (10) (11) 6)当前迭代次数Epoch与最大迭代次数tmax比较,若Epoch>tmax,则终止算法,当前的gbest为BP神经网络优化的权值和阈值,否则跳至步骤2),继续下一次迭代。 两种模型的预测结果如图2所示,其中,N2预测模型为采用本文提出的改进算法建立的模型,N1预测模型为采用传统PSO-BP神经网络的全输入变量算法建立的模型。由图2可知,采用N2预测模型的预测精度高于N1预测模型。为进一步得出两种预测模型误差对比,图3给出了两种模型的绝对误差,由图3可见,N2预测模型的绝对误差远小于N1预测模型。 图2 两种模型预测值与空调冷负荷真实值曲线图Fig.2 Two model predicted values and air conditioning cooling load actual value 图3 两种模型预测值与空调冷负荷真实值绝对误差柱状图Fig.3 The absolute errors between the real values of the air conditioning cooling load and the two 以RMSPE(Root mean square percentage error)(式(12))均方根相对误差作为两种预测模型误差评价指标, (12) 图4 N1模型预测值与真实值回归拟合曲线Fig.4 The regression fitting curve between the predicted value of N1 model and the real 图5 N2模型预测值与真实值回归拟合曲线Fig.5 The regression fitting curve between the predictedvalue of N2 model and the real 提出一种基于改进PSO-BP神经网络算法,实现对冰蓄冷空调动态冷荷的准确预测,结论为:基于灰色关联性分析法,确定影响冰蓄冷空调系统冷负荷的关键因素,并以此作为PSO-BP神经网络预测模型的输入变量,相对于传统PSO-BP神经网络全输入变量预测模型,改进模型在预测精度、收敛速度方面均有较大提高,满足工程实际需求,对大型公共建筑冰蓄冷空调系统的优化运行管理有重要的应用价值。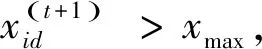
3 预测结果分析


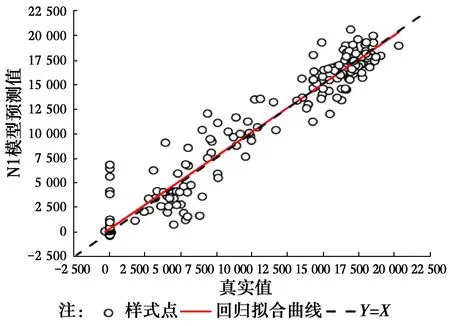
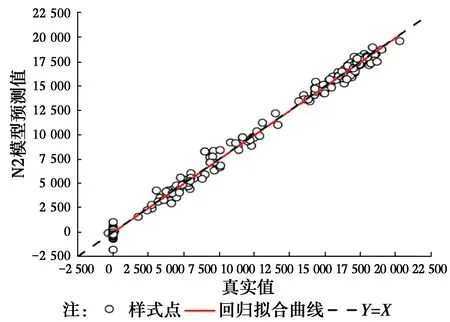
4 结论

