基于时空关系的盾构开挖地表沉降规律
王智德,江俐敏,饶宇,3
(1.武汉理工大学 土木工程与建筑学院,武汉 430070;2.武汉职业技术学院 建筑工程学院,武汉 430074;3.长江科学院 水利部岩土力学与工程重点实验室,武汉 430010)
地铁往往穿越密集的城市建筑群,隧道开挖引起的地表沉降如不加以控制,往往会造成严重的经济损失。在中国,地铁隧道开挖过程中由于地表沉降过大引起的重大事故不乏其例。因此,对地表沉降规律进行研究与预测在工程实践中显得尤为重要。目前常用的预测方法有:工程经验法、理论解析法、数值分析方法、随机介质理论方法、模型试验法以及神经网络与灰色预测等方法[1-3]。魏纲等[4]较早注意到Midlin解在盾构法施工中计算地表沉降的作用;林存刚等[5]研究了盾构掘进速度和非正常停机对地表沉降的影响关系;唐晓武等[6]研究了地表沉降计算公式,并认为适用范围为盾构机头前后2L处,且仅限于施工阶段;孙统立等[7]、陈春来等[8]研究了双线盾构隧道的地表沉降;饶宇等[9]提出了基于Peck公式的地表沉降预测方法;张冬梅等[10]研究了列车振动和地下水耦合下沉降时空规律;林存刚等[11]基于Mindlin解得到了推力、盾构摩擦力、同步注浆压力以及地层损失所引起的地表竖向位移;其他学者[12-16]采用数值模拟、理论分析等方法,并考虑隧道各种影响因素,分析了引起地表沉降的原因。
地表沉降是时间与空间交互影响的结果,准确地讲,地表沉降是动态变化的。然而,多数学者采用单一地表沉降计算公式,忽略了其阶段变化特性。实际上,各个阶段地表沉降计算公式是有显著差异的。其不仅与时间密切相关,且受到盾构推进速度影响。因此,本文基于Mindlin解,综合考虑地表沉降的时空关系和阶段特性,分析各阶段地表沉降的控制因素,推导了地铁隧道盾构开挖引起地表沉降在各个阶段的预测公式,并通过实例验证了公式的有效性。
1 盾构引起地表沉降阶段划分
一般来说,地表沉降大致经历5个阶段:前期沉降阶段、开挖面前的隆沉、通过期间沉降阶段、盾尾间隙沉降阶段和后期沉降阶段。图1和图2是武汉地铁四号线某区间隧道右线监测断面不同监测点的地表沉降速度与推进进度对应图,其中,y值为横断面测点与隧道轴线的距离,m。从图1、图2中可以看出,地表沉降速率有两个峰值,通过时间与盾构机位置的对应分析,可以知道第1个地表沉降速率峰值发生在盾构机通过监测断面正下方,第2个则发生在盾构机尾脱出监测断面瞬间,而第2个峰值往往比第1个更大。在第1个峰值之前,沉降速度由零开始变化,一段时间沉降速度小于零,产生地表隆起;第2个峰值之后,沉降速度迅速下降,直至趋近于零,甚至产生回弹。同时,根据地表沉降速度随时间的变化特点,可将地表沉降的时间序列划分成不同阶段,如图3所示。

图1 右线CJD1断面沉降速度与推进进度对应图Fig.1 Velocity of ground settlement and Advance-time curve of shield machine at the right line monitoring section
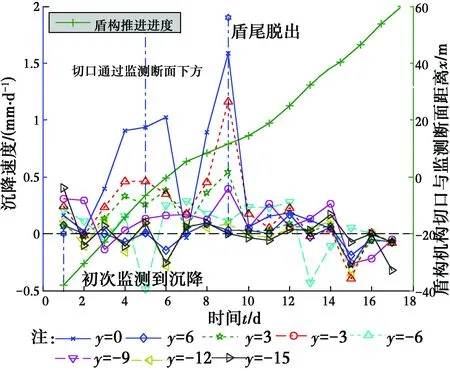
图2 左线CJD1断面沉降速度与推进进度对应图Fig.2 Velocity of ground settlement and Advance-time curve of shield machine at the left line monitoring section 1

图3 地表沉降阶段Fig.3 Stages of the ground
根据图1~图3,沉降规律总结如下:
1)无影响阶段:开挖工作面距离到达监测断面之前35 m以上,地表不产生沉降或者隆起,这一阶段隧道盾构开挖对监测断面土体的扰动几乎没有。
2)前期沉降阶段:范围为开挖工作面距离监测断面35~14 m,尤其在28~14 m范围内,沉降显著增大,这主要是工作面的支护力不足,导致开挖面前方土体向后下移动。特别应该指出的是,由于盾构机顶进推力过大,往往产生土体的隆起。这一阶段监测断面各测点沉降值基本在0.7 mm以内,沉降占比低于10%,甚至由于隆起出现负比值。
3)通过阶段:这一阶段开挖工作面距离监测断面-14~14 m,其中“+”表示监测断面在开挖工作面推进前方,“-”表示开挖工作面已经通过了监测断面。此阶段地表沉降突然急剧增大,隧道轴线中心沉降量达到4 mm左右,各测点沉降占比多处于50%~35%,监测断面边缘个别测点出现沉降比值畸变。
4)盾尾空隙沉降阶段:这一阶段开挖工作面已经离开监测断面14~28 m。通过阶段过后往往沉降速度稍有下降,但是,随后进入盾尾空隙沉降阶段,沉降速度增大,沉降速度峰值往往比通过阶段沉降速度峰值还要大,达到各阶段瞬时沉降峰值。这是由于盾尾间隙过大、盾尾同步注浆效果欠佳造成的[17]。这一阶段应该对注浆质量引起重视。虽出现沉降峰值,但由于注浆凝固的影响,持续时间短暂,沉降值基本在2 mm以下,沉降占比25%~15%。
5)工后沉降阶段:开挖工作面离开监测断面28 m以上,特征是沉降速度迅速降低,但持续时间长,这一阶段沉降占比在20%以下。需要指出的是,这一阶段存在土体回弹阶段,一般发生在工作面离开监测断面6~10 d内产生,此时,工作面已经离开监测断面42 m左右,之后地表沉降趋于稳定。
2 地表沉降规律及影响因素
盾构隧道施工引起的地表沉降规律表现出强烈的空间效应和时间效应,时间的推移反映在空间上就是开挖工作面相对位置的变化。在隧道埋深不变,土层物理力学性质相对稳定条件下,地表沉降的影响因素主要分为盾构开挖附加推力、盾构外壳与土体的摩擦力、同步注浆压力、地层损失以及工后固结沉降[11]。对于施工期各个沉降阶段均受到其中几个或全部因素影响,某些因素占据主导作用。
2.1 模型的建立与Mindlin解
通过上述分析可知,隧道施工过程中随开挖工作面的推进,地表沉降大体经历了5个阶段,地表沉降受到开挖工作面与监测断面相对位置的影响,建立如图4所示的沉降分析模型。盾构机沿x正方向推进,z轴为竖直方向,y轴为横断面方向。
基于Mindlin解假定土体为线弹性半无限空间体。各参数含义:υ为土体泊松比;G为土体剪切模量,MPa;v为盾构机推进速度,m/d;t为盾构机以进入前影响距为起点的时间,d;D为盾构外径(即为隧道直径,m);R为隧道半径,m;L为盾构机长度,m;L1为盾构机通过监测断面前的影响距离,m;L2为盾构机通过监测断面后的影响距离,m;H为轴线埋深,m,如图4所示。

图4 沉降分析模型Fig.4 Settlement analysis

图5 Mindlin公式示意图Fig.5 Schematic diagram of Mindlin
如图5,Mindlin[18]推导均质各向同性半无限空间内z=c深度处作用竖向作用力和水平集中力时,任意一点的竖向位移值S1和S2分别为
(1)
(2)
(3)
(4)
2.2 正面附加推力引起的地表沉降
对于盾构机处于固定位置的正面附加推力、盾构与土体摩擦力以及盾尾注浆压力引起的地表沉降,林存刚等[11]做了较为详尽的推导,如图4。正面附加推力微元dqh=qrdθdr,作用位置c=H-rsinθ;盾壳摩擦力微元dfh=fRdθdl,作用位置c=H-Rsinθ;盾尾注浆压力竖向分力微元dpv=pRsinθdθdl,作用位置c=H-Rsinθ。本文在此基础上,引入时间效应,将地表沉降视为动态变化的,并将转换坐标设定在前方固定位置,以此来研究某一固定监测断面的地表沉降规律。
在各个阶段,转换坐标均保持一致,即(参数具体含义见前文)
(5)
将c=H-rsinθ代入式(3)、式(4),得(其中,上标i=1、2分别对应前影响距阶段和后影响距阶段)
(6)
(7)
(8)
(9)
2.3 盾构与土体摩擦力引起的地表沉降
对变量k作如下定义:
(10)
1)阶段一(通过前阶段一,机体部分在影响范围内):0≤t≤(L/v)
(11)
将c=H-Rsinθ代入式(3)、式(4),得
(12)
(13)
将式(11)~式(13)代入式(2),得
(14)
2)阶段二(通过前阶段二,机体全部在影响范围内):L/v (15) (16) 3)阶段三(通过阶段):(L1/v) 将盾构机分成-l1≤x≤0和0 (17) (18) 4)阶段四(通过后阶段):[(L+L1)/v) (19) (20) (21) 显然,将不同阶段的转换坐标(其中y′=y-Rcosθ,z′=z,x′不同阶段存在差异)代入式(3)、式(4)能得到该阶段的R1、R2。 对于盾尾注浆压力范围,一般为盾尾后一环衬砌的宽度。且假定其沿该环管片均匀分布,在盾尾离开一环管片宽度后,开始拼装管片,瞬时均匀加载。 1)阶段一(通过前阶段):t≤[(L+L1)/v],其中,x′=x+L1+L+b-vt,则: (22) 2)阶段二(通过阶段):[(L+L1)/v] (23) 3)阶段三(通过后阶段):[(L+L1+B)/v] (24) 盾构机刀片在切割土体向前推进时,由于盾构尾部衬砌管片拼接、注浆不及时,注浆压力不够等不可避免地产生土层的整体下沉,产生所谓的地层损失。对于开挖面之前的土体,一般不考虑其地层损失。Loganathan等[19]认为地层损失沿隧道截面成椭圆形分布,在隧道径向不等量。Sagaseta[20]则认为地层损失沿隧道截面径向成均匀等量的圆形,地面沉降槽体积等于土体损失量。其地表的竖向位移计算公式为 (25) 式中:V为地层损失量,大多采用地层损失率的经验方法来计算。V=πR2η,η为地层损失率,一般取工程经验值,R为隧道半径。 转换坐标为:x′=x+L1-vt,y′=y,z′=z。对于某一监测断面地表沉降,地层损失历程为 (26) 在不考虑土体在施工期后固结沉降的情况下,总地表沉降即为以上沉降分量的叠加。 S(t,x,y,0)=SQ(t,x,y,0)+SF(t,x,y,0)+ SP(t,x,y,0)+SV(t,x,y) (27) 需要注意的是,地层损失引起的沉降为地表面的沉降。在计算地表沉降随时间变化的时候,应取z=0,计算监测横断面的地表沉降时,应取z=0,x=0。 通过该计算公式,可以和前面划分的地表沉降阶段很好地对应起来,以此来分析各个阶段影响地表沉降的主导因素,为地铁施工和地表沉降的控制提供依据和指导。 武汉市轨道交通四号线05标段为两站两区间,包括罗家港—园林路区间、园林路站、园林路—工业路区间及工业路站。拟建场地属长江冲积I级阶地,场地为一般粘性土、软土、砂土层。 通过现场实验,参数为:隧道半径R=3 m,盾构机长度L=11.4 m,土体泊松比υ=0.28,土体剪切模量G=10 MPa,隧道埋深H=14 m,正面附加推力q=42 kPa,摩擦力f=88 kPa,注浆压力p=300 kPa,根据第2节,前影响距L1=35 m,后影响距L2=42 m,推进速度v=42环/周=9 m/d,地层损失率根据武汉地区工程经验值[21],取η=0.01。 图6~图9分别为附加推力、摩擦力、注浆压力和地层损失引起的地表沉降变化规律图(y值为横断面测点与隧道轴线的距离,m)。其中,第4天开挖工作面通过监测断面正下方,为地层损失和正面附加推力的通过阶段;第5天盾尾通过监测断面下方,为注浆压力的通过阶段;4~5 d为盾构机身的通过阶段。 图6 附加推力引起的地表沉降Fig.6 Ground settlement caused by additional 图7 摩擦力引起的地表沉降Fig.7 Ground settlement caused by friction 图8 注浆压力引起的地表沉降Fig.8 Ground settlement caused by the grouting 图9 地层损失引起的地表沉降Fig.9 Ground settlement caused by ground 由图6~图9可知,正面附加推力、摩擦力、注浆压力以及地层损失都能很好的与前面所述的无影响阶段、前期沉降阶段、通过阶段、盾尾空隙沉降阶段、工后沉降阶段对应起来。在无影响阶段,各因素引起的地表沉降趋近于零;前期沉降阶段,正面附加推力和摩擦力都引起地表隆起;一旦进入通过阶段,各因素引起的地表沉降迅速增大;盾尾空隙阶段,地表沉降持续增大;此后进入工后沉降阶段。显然,土体回弹现象主要与前3个因素密切相关,之后地表沉降趋于稳定,这与第2节所述的沉降规律吻合。 单从对地表沉降的贡献值来说,前影响距阶段摩擦力和地层损失对地表沉降起到了控制作用;后影响距阶段地层损失起到了主要控制作用;而在整个阶段,正面附加推力、摩擦力、注浆压力和地层损失等4个因素中,以地层损失对地表沉降影响最甚。地表隆起主要由正面附加推力和摩擦力所引起,而工后沉降阶段的土体回弹则与正面附加推力、摩擦力和注浆压力3个因素有关。 图10为地表沉降理论值与现场实测值的比较。由于受到现场施工技术、地质条件等因素影响,难以采用理论公式进行考虑,并且本文做了一定的简化,考虑到受力情况与实际存在差异,实际摩擦力、正面附加推力和注浆压力分布不均并存在测量误差,因此,实测值比理论值稍微偏大。 图10 地表沉降理论值与实测值比较Fig.10 Comparison between the theoretical value and the measured values of ground 1)通过划分施工阶段反映了地表沉降的时间和空间效应,将地表沉降分为5个阶段,并通过现场监测数据分析获得各阶段的大致范围。 2)指出在前、后影响距离范围内,盾构机与土体的摩擦力和地层损失等对地表沉降的影响,确定了导致工后沉降阶段土体回弹的前期沉降阶段各种因素。实际工程中,在施工的各个阶段,需要采取措施对相应的主导因素加以控制。 3)考虑地表沉降的时空关系,推导了实时地表沉降计算的理论公式,实例应用表明:实测值比理论预测值偏大。 笔者主要从理论上推导了盾构开挖引起地表沉降的规律和计算方法,但对于实际施工中存在的摩擦力、正面附加推力和注浆压力分布不均以及如何进行精确测量等问题仍有待进一步研究。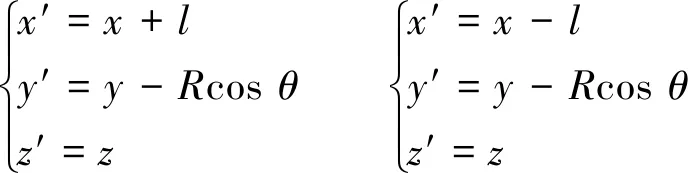
2.4 盾尾注浆压力引起的地表沉降
2.5 地层损失引起的地表沉降
2.6 地表沉降计算公式
3 实例分析



4 结论

