弹性SDOF体系输入能量谱的设计表达式
夏洪流,胡仁杰
(重庆大学 土木工程学院; 山地城镇建设与新技术教育部重点实验室,重庆 400045)
结构地震响应实质上是地震能量在结构中输入、转化与耗散的过程。早在1956年,Housner就提出基于能量的抗震设计概念,认为只要结构耗散能量的能力不小于地震输入的能量,并针对能量耗散的分布形式进行合理设计,就足以保证结构的抗震性能。相较基于承载力的设计方法,基于能量的抗震设计方法考虑了结构的累计损伤,可更全面反映地震作用的特性及对结构的影响[1]。
地震动输入能研究一直是能量法研究的核心内容之一,学者们就此展开大量相关研究。Akiyama[2]基于四类场地提出两段式设计输入能量谱;Benavent-Climent等[3]采用哥伦比亚地震动记录建议了两段式设计输入能量谱;程光煜等[4]、陈清军等[5]分别采用能量谱峰值与面积归一化的方法,建议了弹塑性SDOF体系三段式设计输入能量谱;屠冰冰[6]提出适用于中国场地条件分类的弹塑性SODF体系归一化等效速度谱计算方法;陶云芳等[7]、屠冰冰等[8]采用等效线性化等方法对弹塑性能量谱进行了估算。上述研究虽对地震动输入能量谱给出了多种形式的表达,但由于能量响应的随机性,分析结果依赖于样本与假定,造成现有研究结论存在较大差异,且尚未给出输入能量谱峰值(沿用文献[4]的定义,为0~6 s周期范围内输入能量谱的最大值)的合理计算方式,从而导致无法得到一致认可的SDOF体系输入能量谱设计表达式。鉴于弹性输入能量谱是地震动输入能研究的关键基础,本文拟以更具普适性的强震记录为基础,考虑多种场地条件下研究弹性输入能量谱的影响因素,进而给出设计表达式,为后续研究奠定基础。
以涵盖多种场地条件的强震记录为基础,对弹性SDOF体系输入能量谱设计表达式展开研究,具体思路为:利用NGA地震动数据库,通过筛选得到分析样本;基于时程分析,得到各条地震动弹性输入能量谱;通过相关性分析,寻找EImax与地面运动参数的关系,据此建立EImax的回归表达式;基于归一化输入能量谱曲线特性研究,给出阻尼比为0.05的SDOF体系弹性设计输入能量谱的计算方法。
1 能量法概念
水平地震作用下,单自由度体系的运动微分方程为
(1)

(2)
式中:从左到右各项依次为以相对位移为基础的体系动能EK(t)、阻尼耗能ED(t)、吸收能EA(t)、地震动输入能EI(t),即得到SDOF体系的能量计算表达式为
EK(t)+ED(t)+EA(t)=EI(t)
(3)
式中:吸收能EA(t)由弹性吸收能ES(t)与滞回耗能EH(t)组成,而对于弹性SDOF体系,滞回耗能EH(t)为零。在地震结束时,结构动能EK(t)和弹性变形能ES(t)几乎为零,结构的耗能能力主要取决于阻尼耗能ED(t)。因此,在确定阻尼比之后,通过逐步积分法(计算时采用Newmark-β法)迭代计算结构响应,即可得到特定阻尼比下弹性单自由度体系的输入能量谱与阻尼耗能谱。
2 强震记录的选择
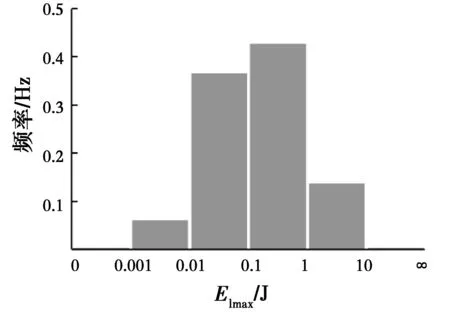
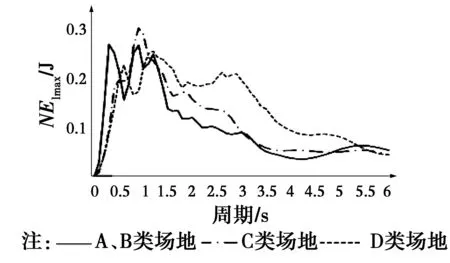
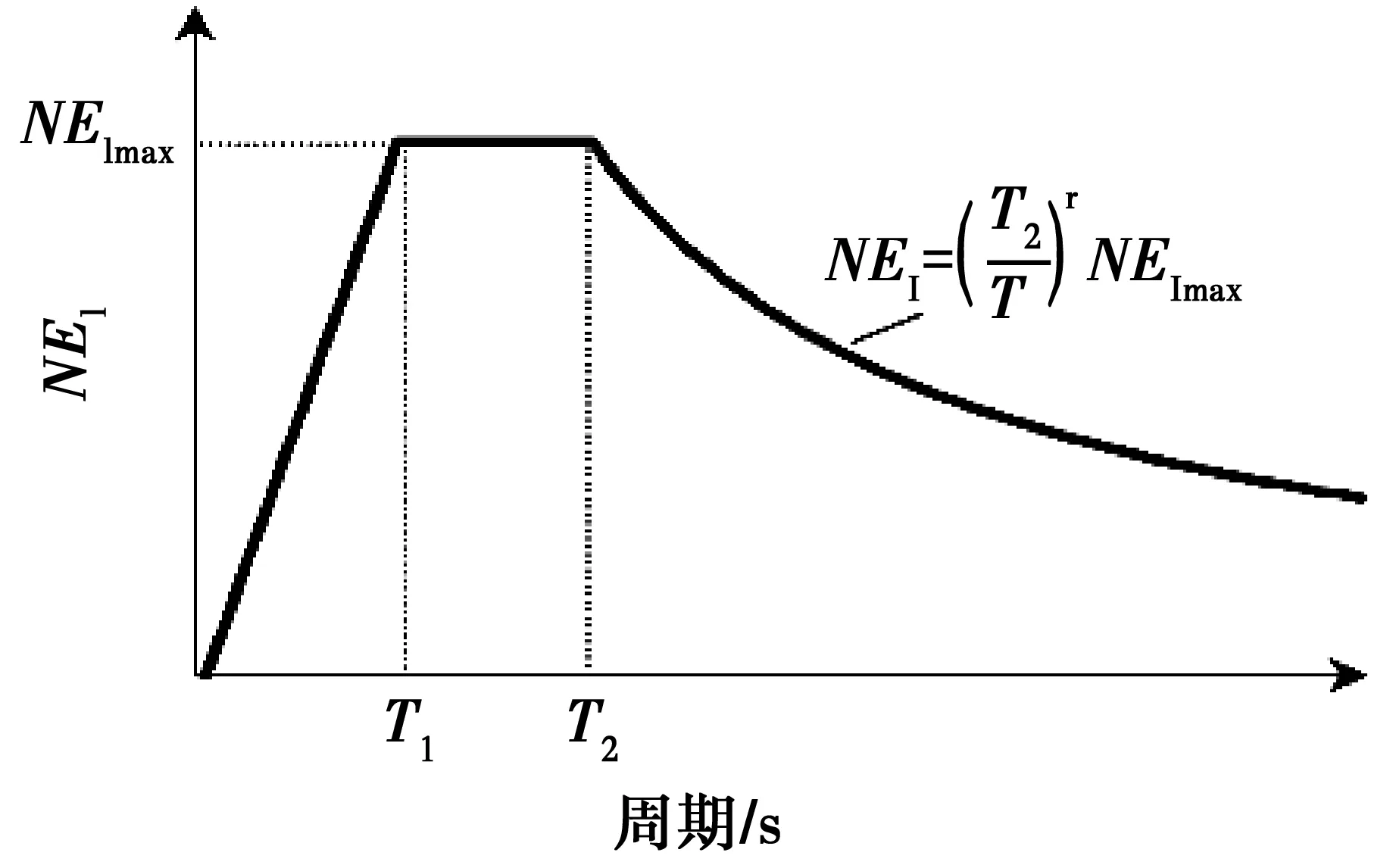
目前,关于输入能量谱的研究结论存在较大差异,一定程度上是因为强震记录样本缺少统一的选择原则。为保证数据样本的可靠性与代表性,从太平洋地震工程研究中心NGA地震动数据库进行地震动样本筛选。鉴于场地条件是影响地震动工程特性的重要因素,而目前规范对场地条件划分的标准存在一定差异,文献[9-10]的研究成果表明,取表层30 m范围内等效剪切波速Vs30包含更全面的场地信息,更能充分反映场地分类的影响。因此,本文参照NEHRP推荐的场地条件划分标准,筛选出276条地震动记录,其中A、B类场地(硬基岩和基岩,Vs30>760 m/s)61条,C类场地(非常坚硬土或软基岩,360 图1 震级与断层距分布Fig.1 Distribution of magnitude and hypocentral 现有关于输入能量谱的研究成果多采用两段式或三段式能量谱模型[2-6],这两类模型的区别主要体现在对能量谱长周期段的描述,但目前没有充足的证据表明哪类模型更具代表性。为尽量真实地反映输入能量谱的客观规律,输入3种场地条件下强震记录,计算阻尼比为0.05的SDOF体系(m=1 kg)在周期0~6 s范围内的弹性输入能量谱,研究场地条件对输入能量谱的影响和输入能量谱的基本特征。 经统计,总体样本的输入能量谱曲线由于样本覆盖的震级、震中距、场地等条件极为广泛,因此,呈现出很大的离散性,不利于基于能量的设计应用。仅就输入能量谱峰值EImax这一个指标,经简单统计可以发现(如图2所示),EImax最小值为0.000 726 0 J,最大值达14.95 J,相差达5个数量级。显然,不加分类地进行平均,看似涵盖所有强震记录的能量特征,但实质上不能揭示影响输入能量谱峰值的影响因素。进一步对总体样本记录能量谱峰值周期Tpe(即输入能量谱Elmax中对应的结构周期)分布进行统计(如图3所示),可见Tpe集中分布于中、短周期段,其中90.58%的强震记录Tpe分布于0~2.5 s区间。 图2 Elmax分布图Fig.2 Distribution of Elmax 图3 Tpe分布图 需要注意的是,通过弹性输入能量谱试算,3种场地条件下都发现少数强震记录的输入能量谱卓越周期Tpe分布于长周期段(如图4(a)中圆圈所示),尤其在代表坚硬场地的A、B类地震动记录中,也出现了少量Tpe为3 s以上的情况,这与现有概念“坚硬场地上的能量反应应集中在中短周期段”存在矛盾。通过进一步傅里叶分析发现,这部分地震波的加速度傅里叶幅值谱都具有多个频率差距较大的峰值,输入能量谱也多呈现为特殊的多峰型曲线。鉴于此类地震动记录占比较少,且多峰型能量谱通常是由于震源机制、传输机制及场地影响等多因素耦合造成,在目前缺少系统性统计和足够样本数量前提下,暂不纳入本文研究范围。因此,后续对具有明显双峰型傅里叶加速度谱的地震动记录予以筛除,筛除程序为:首先,计算出各条地震波的傅里叶加速度谱,其次,计算出谱曲线上第1主峰和第2主峰对应周期值,当第1主峰值与第2主峰值对应周期相差大于等于2 s时,判定为双峰谱,对此类地震波进行筛除。图4为全集系地震动记录归一化输入能量谱在筛除双峰谱前后的对比情况。据此标准筛选后,地震动样本数量为259条(含A、B类场地54条,C类场地102条,D类场地103条),占原样本总体的93.8%,后续研究均据此样本集开展。 图4 地震动记录筛选前后的归一化输入能量谱对比Fig.4 Comparison of ground motions before and after being 鉴于上述计算的输入能量谱涵盖了多个震级、多种场地类型和跨度较大的断层距地震动记录,直接对输入能量谱进行统计分析,必然存在很大的离散性。参考文献[4],将输入能量谱表征为Elmax与归一化输入能量谱曲线的乘积,可以更好地对输入能量谱特性进行分析。针对的259条地震动记录,统计3种场地条件下的平均输入能量谱(如图5所示)。3种场地条件平均输入能量谱均呈现出明显的上升段、平台段和下降段,因此,选择三段式能量谱模型更为恰当。参考文献[4-6]关于三段式归一化输入能量谱函数表达形式,取归一化输入能量谱(NEI)回归函数模型为 (4) 式中:NEI为阻尼比ξ=0.05时SDOF体系归一化弹性输入能量谱值;T1和T2分别为平台段的起始周期和结束周期;r为下降段的衰减系数,输入能量谱模型如图6所示。 图5 弹性平均输入能量谱Fig.5 Elastic mean input energy 图6 归一化输入能量谱模型|Fig.6 Input energy spectrum 关于输入能量谱峰值EImax已有大量的研究成果[4,11-13],但缺少各类指标对EImax影响的相关性对比分析。为了确定地震动参数与弹性输入能量谱之间的关系,收集整理了13个地震动参数用以进行分析对比,其中,包括峰值加速度(PGA)、峰值速度(PGV)、峰值位移(PGD)、均方根加速度(Arms)、均方根速度(Vrms)、均方根位移(Drms)、绝对累积速度(CAV)[14]、Arias强度(Ia)、Park特征强度(Ic)[11]、Riddell等[12]、Fajfar等[13]和程光煜等[4]分别提出的地震动强度指标IR、IF、Ich,各参数定义说明如表1所示。鉴于地震动能量响应的物理意义,速度时程的傅里叶幅值谱与输入能量谱谱值具有直接相关性,且试算表明这两条谱曲线具有较为一致的曲线分布形式,因此,基于傅里叶变换提出新的地震动参数(Ise)。 表1 地震动参数定义说明Table 1 Explanations of ground motion parameters 参考文献[12]回归方程,对输入能量谱峰值EImax采用式(5)所示拟合表达式。 (5) (6) 图7 各参数与EImax相关性系数Fig.7 Correlation coefficients between different 为确定不同震级、震中距和场地条件下Ise取值,针对Ise的衰减规律展开进一步研究。参考文献[15-16]对输入能量谱衰减规律的衰减模型与研究成果,基于259条地震动数据,利用最小二乘法进行Ise衰减规律的回归,结果为 (7) 式中:M为矩震级;Rrup为断层距;Gc和Gd分别为考虑场地影响而引入的已知函数,当场地条件为C类时,Gc=1,其他场地条件时,Gc=0;当场地条件为D类时,Gd=1,其他场地条件时,则Gd=0。其他常数项均为回归分析的结果,其中,随机误差的均方差σ(lgIse)=0.198。 场地条件是影响输入能量谱频谱特性的重要因素,整理不同场地条件下的分布情况,结果如图8所示。3种场地条件下的分布存在明显差异,随场地条件变软,平均值逐渐增大(A、B类场地为0.776 s,C类场地为1.027 s,D类场地为1.185 s),总体分布有向长周期移动的趋势,因此,有必要考虑场地条件对输入能量谱的影响。 图8 不同场地条件下Tpe的分布情况Fig.8 Distribution of for different site conditions 为准确分析输入能量谱曲线分布特征,利用EImax对各条输入能量谱进行归一化,基于归一化输入能量谱进行研究分析。基于场地条件的划分,输入259条地震动记录,统计阻尼比为0.05的单自由度弹性体系的平均归一化输入能量谱曲线,并基于式(4)的形式,利用最小二乘法进行曲线拟合,拟合谱相关参数见表2,拟合谱曲线如图9所示。由表2可见,随场地变软,输入能量谱卓越区段向长周期移动,T1和T2逐渐增加,下降段衰减系数r逐渐增大。将由式(6)计算得到的能量谱峰值与归一化输入能量谱拟合谱相乘,即可得到本文建议的弹性设计输入能量谱。 图9 平均归一化输入能量谱与拟合谱的对比Fig.9 Comparison of average normalized inputenergy spectrums and fitted 场地类别T1T2tNEImaxA、B类场地0.121.250.820.33C类场地0.451.451.270.40D类场地0.521.671.300.40 为检验研究成果的有效性,基于式(7),在NGA数据库中另行随机选取C、D类场地纪录15条和21条,其强度指标lgIse分布区间为[-0.067,-0.064]。图10为两种场地条件下抽样记录平均输入能量谱与本文拟合谱计算结果的对比,由图可见,本文提出的拟合谱与平均输入能量谱曲线吻合良好,其中,C类场地平均相对误差为19.78%,D类场地为15.03%。抽样验算的结果表明,本文弹性设计输入能量谱能较准确地反映不同场地条件下平均输入能量谱的统计特征。 图10 抽样平均输入能量谱与拟合谱的对比Fig.10 Comparison of sample mean input energy 基于3种场地条件下259条地震动记录,利用时程分析和归一化方法,研究分析了SDOF弹性输入能量谱的基本特征。结论如下: 1)通过相关性分析,提出作为评价输入能量谱幅值的地震动参数指标是合适的,并采用最小二乘法确定了Ise、Elmax的表达式。 2)SDOF弹性平均输入能量谱曲线受场地条件影响显著,依据NEHRP推荐的场地划分准则,3种场地条件下平均输入能量谱曲线均具有三段式函数形式;经回归分析,得到结构阻尼比为0.05时,各种场地条件下平均输入能量谱曲线特征参数的具体取值,确定了平均输入能量谱表达式。计算结果表明,随场地变软,平均输入能量谱卓越区段向长周期移动,拟合谱的平台起止点和逐渐增大,下降段的衰减系数逐渐提升。 3)通过Ise、Elmax表达式、归一化输入能量谱拟合谱曲线组合,即可得到不同震级、断层距与场地条件下建议的平均输入能量谱,算例结果表明,本文建议表达式能较准确地反映不同场地条件下平均输入能量谱的统计特征。
3 输入能量谱计算样本筛选及谱曲线函数形式


4 输入能量谱峰值与地震动特征参数间的相关性分析

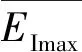


5 弹性输入能量谱的建立与验证




6 结论

