基于谐波效应补偿的对称六相与三相PMSM串联系统解耦控制研究

闫红广，刘陵顺,王 赛,郭 鹏

(1.海军航空大学 航空基础学院，山东 烟台 264001；2.91206部队,山东 青岛 266000)

0 引 言

在航空航天、舰船电力推进、多电飞机和电动汽车等应用场合，电力传动装置的体积和重量受到严苛限制，效率高、重量轻、成本低的电力驱动系统一直是业界的追求目标[1]。多电机传动系统是运动控制研究领域的重要内容，随着现代电力电子技术和现代电机控制技术的发展，单逆变器多电机串联驱动系统作为一种新颖的多电机系统开始受到学者关注。在这种系统中，多电机串联解耦运行的理论基础是构成串联系统的电机均为正弦波磁动势电机[2]。但是，由于材料、设计、制作工作和误差等原因，电机内部不可避免地存在多种空间谐波，串联系统的解耦运行可能受到影响。

在2000年IEEE的工业应用大会上，Gataric S.将传统的多相电机系统变换到互相垂直的多维平面，仿真实现了4个自由度控制下两台五相感应电机的解耦运行[3]。文献[4]总结了这类串联系统的构成和解耦变换阵的选取规则，指出在电机相数足够多的情况下，这种解耦控制理念原则上可以实现任意多台电机的串联解耦控制。对于单逆变器驱动的对称六相与三相电机串联系统，文献[5]详细分析了该串联系统中两台电机相电流关系、磁通产生及分布特点，阐明了解耦控制原理。文献[6]采用扩展卡尔曼滤波器设计两台电机的位置观测器，仿真实现了串联系统无位置传感器的解耦控制。在文献[7]给出的六相电机相电流波形中含有明显的低次谐波成分，正弦度较差，电机的转速、转矩脉动较大。对此，文献[8]分析了低次谐波的分布规律，并进行了开环实验验证，但文中没有进行考虑谐波效应的串联系统解耦控制研究。文献[9]仅考虑了六相PMSM反电势含有2次谐波的情况，没有考虑三相PMSM空间2次谐波问题和绕组非正弦分布问题。

本文以单逆变器驱动的凸极式对称六相与三相PMSM两电机串联系统为研究对象，针对两台电机含有空间2次谐波的情况，通过建模和仿真，研究2次谐波在串联系统中的分布规律和对串联系统的影响。进一步，根据所建立的数学模型和两台电机的实时运行状态，在两台电机的转矩控制环节进行合理补偿，以期消除转矩上的脉动量，并最终实现两台电机的解耦运行。

1 考虑空间2次谐波的串联系统数学模型

图1 对称六相串联三相PMSM系统示意图

单逆变器驱动的对称六相与三相PMSM串联系统及其定子绕组连接关系如图1所示。设Is1=[iAiBiCiDiEiF]T、Is2=[iUiViW]T为两台电机定子绕组上的电流，且有逆变器电流Is=Is1；Rs1、Rs2为两台电机定子电阻矩阵，且有Rs1=rs1E6，rs1为六相电机相绕组电阻，E6为六阶单位阵；Rs2=rs2E3，rs2为三相电机相绕组电阻， 为三阶单位阵。

在文献[9]的基础上，应用绕组函数法和倒气隙函数法[10]，可以得到同时考虑绕组2次谐波和反电势2次谐波的六相PMSM的定子磁链方程为

Ψ1=(Lsσ1E6+Lm1Em1+Lm2Hm2+Lm3Hm3+

Lm4Hm4)Is1+ψf11F11+ψf1212F12

(1)

式中，Ψ1表示六相电机定子磁链，Lsσ1为六相电机的相绕组自漏感(忽略相绕组互漏感)，Hm1、Hm3分别为六相电机基波、2次谐波电感矩阵中与相绕组位置相关的部分，Hm2、Hm4分别为六相电机基波、2次谐波电感矩阵中与转子位置相关的部分，Lm1、Lm3、Lm2、Lm4为与电机参数相关的矩阵系数。θr1为六相PMSM转子位置，θ1=π/3，ψf11、ψf12分别为六相PMSM永磁体产生的气隙磁密基波、2次谐波交链其定子绕组侧的磁链幅值。

同理得到三相PMSM的定子磁链方程为

(2)

式中，Ψ2为三相电机定子磁链，Lsσ2为三相电机的相绕组自漏感(忽略相绕组互漏感)，Hn1、Hn3分别为三相电机基波、2次谐波电感矩阵中与相绕组位置相关的部分，Hn2、Hn4分别为三相电机基波、2次谐波电感矩阵中与转子位置相关的部分，Ln1、Ln3、Ln2、Ln4为矩阵系数。θr2为三相PMSM转子位置，θ2=2π/3，ψf21、ψf22分别为三相PMSM永磁体产生的气隙磁密基波、2次谐波交链其定子绕组侧的磁链幅值。

两台电机的定子电压方程分别为

(3)

(4)

按文献[5]中的方法，将三相电机相关矩阵进行扩展，叠加得到串联系统定子电压方程

(5)

为了便于实现解耦控制，需要对串联系统在自然坐标系下的数学模型进行clark、park变换。根据串联系统中电机结构及绕组连接关系，串联系统的六维clark变换矩阵为[5]

(6)

根据实变换基本理论，采用变换矩阵T将自然坐标系下逆变器输出电压变换到三个相互正交的αβ-xy-o1o2平面。根据变换矩阵的特点可知，经过变换，αβ平面为六相电机的基波平面，xy平面为三相电机的基波平面。若两台电机之间不存在耦合，分别改变αβ平面和xy平面的相关控制量，就可以分别实现对两台电机的控制。

根据两台电机的park变换矩阵，可以取串联系统的park变换阵为

(7)

T2=RT

(8)

令Udq=[ud1uq1ud2uq2ud3uq3]T、Idq=[id1iq1id2iq2id3iq3]T分别表示串联系统在静止坐标系下的电压矩阵和电流矩阵，则

(9)

将式(5)、式(8)代入式(9)得到

(10)

采用对磁共能求导的方法[11]，得到

(11)

同理得到三相PMSM的转矩方程为

(12)

式中，p1、p2分别为两台电机的极对数。

可见，当绕组中存在空间2次谐波时，六相PMSM的空间2次谐波与三相PMSM基波电流发生耦合，并在六相PMSM转矩上产生耦合转矩，导致串联系统不解耦；同时，三相PMSM的2次谐波项仅存在于三相电机平面，不对六相电机产生影响。

2 基于谐波效应补偿的串联系统解耦控制策略

2.1 基于谐波效应补偿的串联系统解耦控制策略

在两台电机各自同步旋转坐标系下进行电流给定时，对耦合转矩和谐波转矩进行补偿消除。

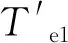
(13)

(14)

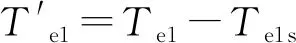
(15)

由式(13)可以看出，在六相PMSM的转矩控制环节引入补偿量-Te1s，六相PMSM最终的电磁转矩中将不再含有空间2次谐波的耦合量。此时，若三相PMSM的运行状态发生改变，六相PMSM将不再受到影响。

同理可得

(16)

(17)

(18)

在三相PMSM的转矩控制环节引入补偿量-Te2s，三相PMSM最终的电磁转矩中将不再含有其自身产生的空间2次谐波转矩。

根据以上分析，设计基于谐波效应补偿控制策略的串联系统控制框图如图2所示。

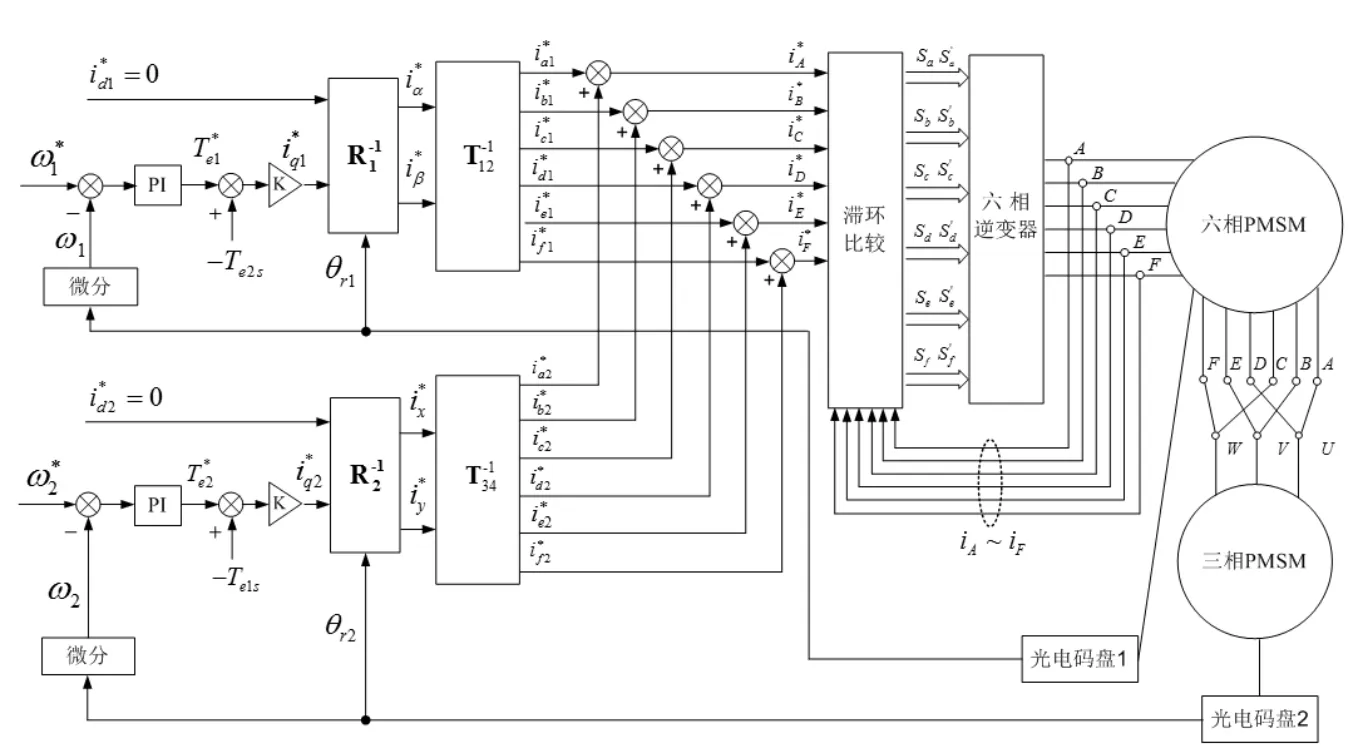
图2 基于谐波效应补偿的串联系统解耦控制原理图

2.2 控制策略的稳态仿真研究

给定六相电机转速500r/min，转矩2.7Nm；给定三相电机转速200r/min，转矩2Nm，对串联系统的稳态工作特性进行仿真，仿真结果如图3所示。

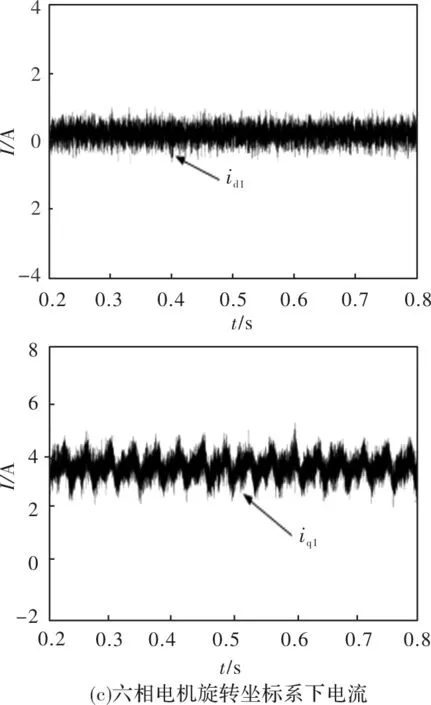
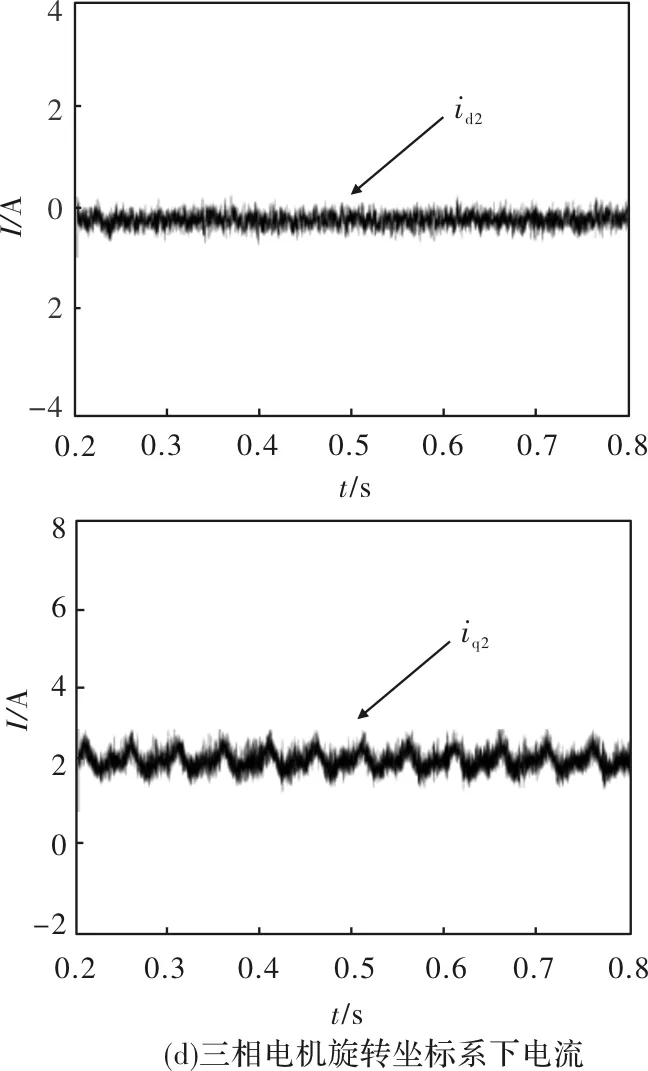
图3 基于谐波效应补偿的稳态仿真结果

由图3中的仿真结果可知：

(1)稳态情况下，两台电机的转矩、转速都能够跟踪给定，两台电机转矩上空间2次谐波所产生的转矩脉动不复存在。

(2)对于两台电机各自旋转坐标系下的电流量iq1、iq2，因引入了补偿量而含有交流成分。

为分析iq1、iq2的交流成分，分别进行FFT分析，结果如图4所示。

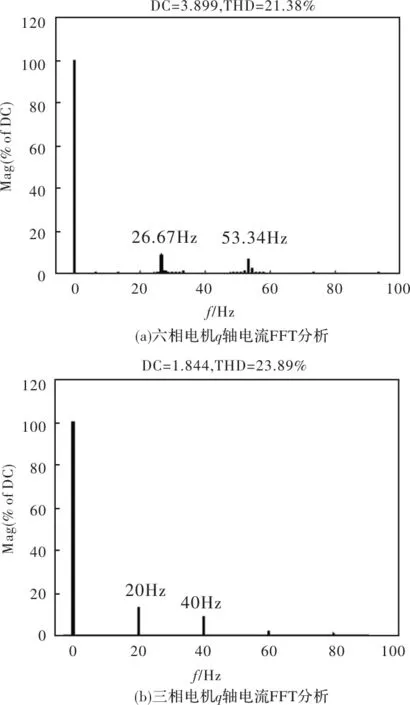
图4 FFT分析结果

FFT分析显示iq1上的交流分量频率为26.67Hz、53.34Hz，对应(2f1-f2)、(4f1-2f2)。iq2上的交流分量频率为20Hz、40Hz，对应3f2、6f2。

从仿真结果可知：

(1)稳态时，两台电机的转矩、转速都能够跟踪给定，两台电机转矩上空间2次谐波所产生的转矩脉动不复存在。

(2)对于两台电机各自旋转坐标系下的电流量iq1、iq2，因引入了补偿量而含有交流成分。

(3)FFT分析显示iq1上的交流分量频率为26.67Hz、53.34Hz，对应(2f1-f2)、(4f1-2f2)。iq1上的交流分量频率为20Hz、40Hz，对应3f2、6f2。

2.3 控制策略的动态仿真研究

在稳态运行的基础上，分别进行两台电机的转速、负载突变情况的仿真，结果如图5所示。

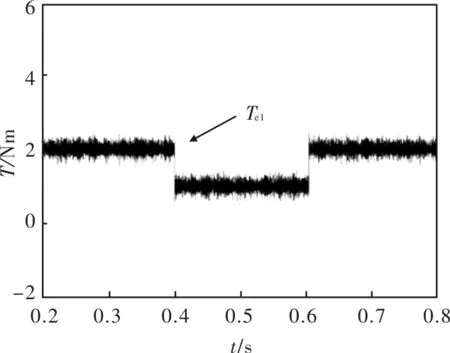
图5 串联系统动态仿真

由图5可知，引入转矩补偿后，两台电机的转矩控制环节脉动转矩分量被消除，最终，一台电机的转速、转矩发生突变时，另一台电机的运行状态不受影响，两台电机可以实现解耦运行。

3 结 论

本文以串联系统的两台电机含有空间2次谐波为例，建立了考虑电机空间2次谐波的串联系统数学模型。通过仿真研究的方法揭示了对称六相与三相PMSM串联系统中空间2次谐波的耦合规律。提出了一种基于效应补偿的串联系统解耦控制策略。仿真结果表明，所提控制策略最终消除了两台电机的耦合量，实现了串联系统的解耦运行。