一种新型双层绕组无铁心永磁直线电机的优化设计

梅威虎，卢琴芬

(浙江大学 电气工程学院，杭州310027)

0 引 言

现代工业生产中，很多应用场合都需要直线运动，永磁直线电机(PMLM)因无须齿轮、丝杠等中间传动装置，直接产生直线运动而得到了广泛的应用。PMLM具有多种结构，其中无铁心结构具有推力波动低、响应速度快、控制方便等特点，在精密定位系统，如光刻机、数控机床、半导体加工设备等，具有重要的应用[1-2]。

无铁心PMLM的研究目前主要有理论计算、有限元分析、优化设计与实验测试等。浙江大学的刘晓和张玉秋等通过解析计算、仿真验证的方法，给出了双边无铁心PMLM气隙磁密的解析公式，分析了电机结构参数对气隙磁密大小和分布的影响，也得出了电枢电流对电机推力的解析公式[5-7]。哈尔滨工业大学的张鲁等提出将“T”字型的Halbach永磁阵列用于双边无铁心永磁直线电机，并建立了该种电机的数学模型[8]。哈尔滨工业大学的李立毅等给出了采用分布绕组的无铁心PMLM解析计算模型，并通过了样机验证[9]。美国威斯康星大学的Seun Guy Min等提出了三相分层的线圈结构，即将三相线圈分为三层，同一相线圈置于同一层中，在增大绕组系数的同时避免了分布绕组线圈端部重叠导致的空间占用问题，并详细计算了各种槽极配合下使用分层方法时线圈的宽度配比，具有一定的指导意义[10]。

无铁心PMLM因为其初级为空心结构，没有导磁材料，因此气隙磁密大幅降低，推力密度往往小于相同体积下的有铁心PMLM。推力密度的欠缺也限制了无铁心PMLM的应用范围。因此，以上无铁心PMLM的很多研究都关注于有效提高推力密度，常见的方法有两种。第一种是从永磁体入手，增大气隙磁密，如采用双边型结构和Halbach永磁阵列[3-4]。另一种方法则是从电枢绕组入手，如采用端部重叠的分布绕组提高线圈的绕组系数、改善加工工艺提高线圈密度等。其中，采用端部重叠的分布绕组是很有效的措施，因为其有效提高了绕组系数，缺点是绕组端部结构很复杂，不仅加工困难，而且端部空间大。

结构参数的优化设计也是无铁心PMLM的一个重要研究方向。电机优化设计是一个多维非线性问题，在不同的应用场合下关注的性能参数也不尽相同。有限元分析法虽然计算精度高，但是计算速度慢，直接应用于无铁心PMLM优化设计时计算时间会很长。因此，将有限元分析法与遗传算法、粒子群算法、重心邻域算法等多种优化算法相结合，快速准确地找出满足特定需求的结构参数是目前无铁心PMLM优化设计的主要方法[11-13]。

为了解决这个问题，本文提出了一种新型双层绕组无铁心PMLM (DW-IPMLM), 其次级由双边结构的Halbach永磁阵列构成，初级由双层绕组构成。绕组每一单层是集中绕组，双层叠置后能起到与分布绕组相近的绕组系数，同时又没有分布绕组复杂交叠的线圈端部制约，节约电机的端部空间，从而提升了推力密度。同时，基于遗传算法对该电机进行了结构优化。最后，制造了样机并由测试验证了分析结果。

1 拓扑结构

图1显示了新型DW-IPMLM的一种拓扑机构，初级由9个集中绕组构成，相当于分布在9个虚拟槽中，即槽极配合为初级9槽次级6极(9s/6p)。每一相包含3个线圈，分相方式显示在图1中，其分置成二层，上一层为4个线圈，从左到右分别为A、B、C、A相，下一层为5个线圈，从左到右分别为B、C、A、B、C。显然，两层绕组都为端部非重叠的集中绕组，其通过非导磁材料封装或固定。这种将三相绕组置于两层的优势在于，可以尽可能地提升单个线圈的绕组系数，又免除了单层分布绕组线圈端部重叠从而带来的空间占用、加工困难等问题。次级由两段式Halbach永磁阵列和背铁构成双边结构，Halbach永磁阵列不仅能够提供更加正弦化的气隙磁场，而且能有效地增大气隙磁密。

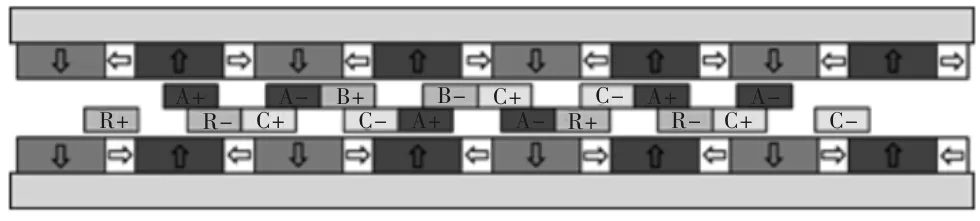
图1 一种9s/6p新型DW-IPMLM示意图

显然，在该结构中，采用整距方式时绕组系数最大，即线圈的两个线圈边相差一个极距，从而反电动势相差180°电角度。然而，考虑到实际线圈宽度在空间上的限制，同一线圈两线圈边难以跨越一个极距的范围，因此需要通过全局优化来确定结构参数。

2 结构优化

新型DW-IPMLM的结构参数如图2所示，包括永磁体、线圈、背铁与气隙的尺寸。在相同有效体积和相同铜耗条件下，为了得到最大推力密度，需要采用全局优化算法优化相应的结构参数。在优化过程中也加入了约束条件，包括线圈匝数、电机总厚度、有效高度等，如表1所示。单线圈边截面积S保持不变可以保证每个线圈的匝数基本相同，进而保证铜耗基本不变。因此，在设定了表1所示的参数不变的前提下，能保证电机的有效体积与铜耗基本不变。

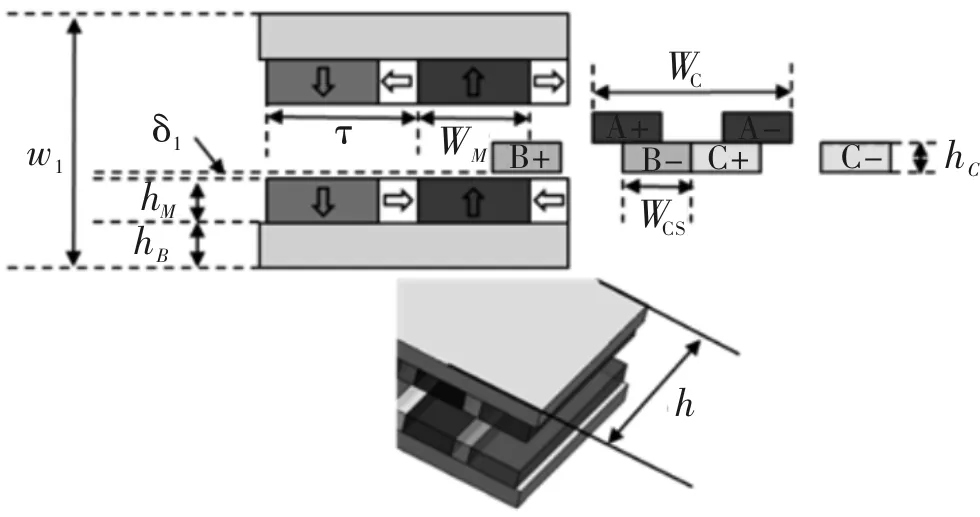
图2 DW-IPMLM的结构参数

全局优化的优化目标是力性能，即最大推力密度与最小推力波动。电机的推力波动定义在一个电角度周期内推力波动峰峰值与平均推力的比值。由于有效体积已经确定，因此以最大值平均推力与最小推力波动作为优化目标。为了量化这一标准，定义一个推力性能系数k，如式(1)所示，为电机平均推力与推力波动的比值。最终电机优化目标是使推力性能系数k达到最大值。

(1)

表1 全局优化中结构参数的约束值

表2 优化变量及变化范围

优化变量为6个，包括永磁体的厚度hM与宽度wM、背铁厚度hB、单线圈边宽度wCS与宽度hC、绕组与永磁体气隙δ1，其变化范围如表2所示。优化变量hM,hB，δ1和hC之和为电机总厚度h，如式(2)所示，因此除满足表2所列的变化范围外，这4个变量之和应该保持不变。

h=2×(hM+hB+hC+γ)

(2)

优化算法选择遗传算法，计算代数设定为1100。电机的计算模型基于Ansys Maxwell建立。通过分析计算，可以得到1100组不同结构参数的电机力性能，如图3所示。可以看出，采用全局优化得到的优化结果考虑了参数耦合的影响，平均推力和推力波动最终都在某一区域收敛。其中平均推力收敛到185N左右，推力波动能收敛到接近1%。

由图3也可以看出，最大平均推力和最低推力波动不是在同一个点。根据设定的优化目标，最终的优化点为图3中箭头所指的位置，此处的电机推力性能系数k为107.5(N/%)，为1100组结构参数中的最大值。相应的结构参数显示如表3所示。

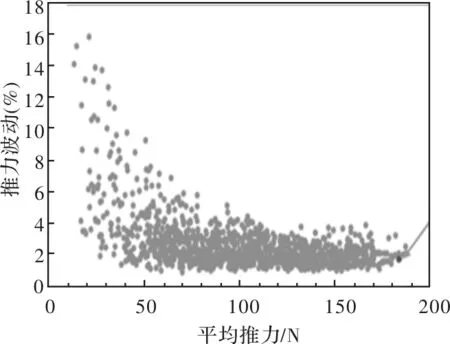
图3 全局优化结果分布图

参数优化值背铁厚度hB/mm4.2永磁体厚度hM/mm7.6永磁体宽度wM/mm15.9永磁体间气隙厚度δ/mm10.0绕组与永磁体气隙δ1/mm1.1单线圈边宽度wCS/mm9.3单线圈厚度hC/mm3.9平均推力Fave/N182.8推力波动FRipple1.7%

3 绕组系数

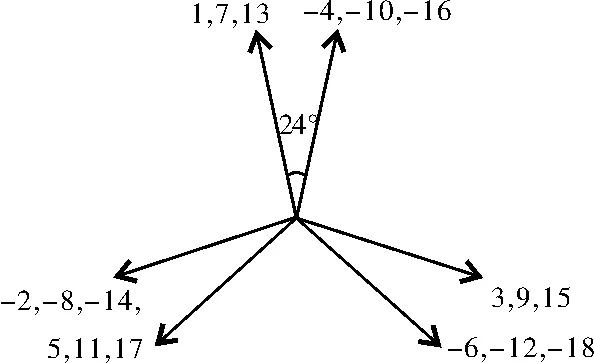
(a)双层绕组

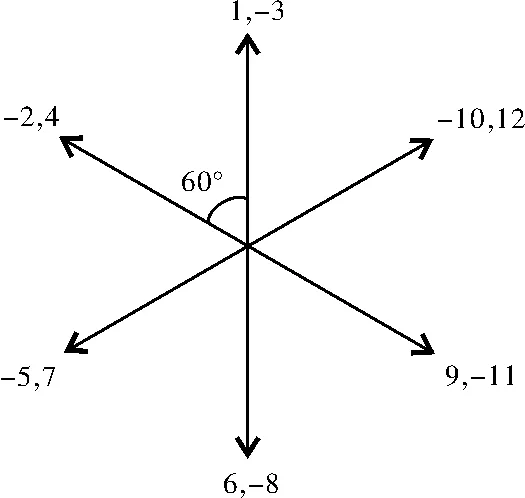
(b)集中绕组

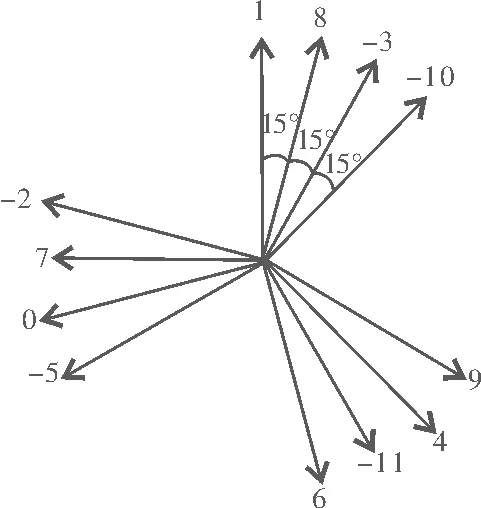
(c)分布绕组图4 反电动势相量图

由表3的结构参数，可以计算该优化方案的绕组系数，其反电动势相量图如图4(a)所示。为了比较，也给出了9s/6p电机采用集中绕组和分布绕组时的反电动势相量图，如图4(b)和图4(c)所示。图中画出了每个线圈边的反电动势相量，并加用编号表示，若数字前加上“-”号，则表示该相量经过了180°电角度的旋转。3种绕组结构的绕组系数可由式(3)计算得出。

(3)

式中，kw1_1、kw1_2、kw1_3分别为电机双层绕组、集中绕组和分布绕组结构时的绕组系数。

显然，双层绕组结构的绕组系数高于集中绕组和分布绕组结构，而且比集中绕组结构高很多。因此，通过采用两层集中绕组，提出的新型电机不仅有效提高了绕组系数，而且保留了集中绕组结构简单的优势，从而线圈利用率更高。

4 性能分析

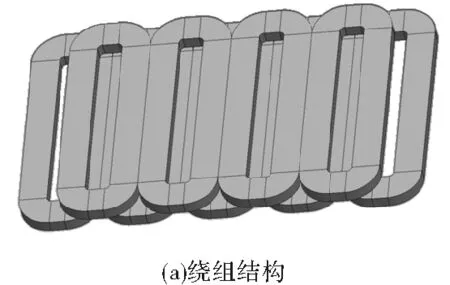
图5 DW-IPMLSM的3D模型

新型DW-IPMLM优化方案的绕组结构如图5(a)所示，显然由于采用了集中绕组组成的双层绕组结构，其绕组端部非常短，占有的空间小，且加工非常方便，具有明显的优势。图5(b)给出了整机的3D有限元模型，基于该模型，能够计算出电磁性能，包括磁链、推力、反电动势等。

4.1 空载磁链

图6(a)为运动速度设定为2.02m/s时电机的空载三相磁链，相应的谐波分析结果如图6(b)所示。由图中可见，空载磁链的正弦性较好，3次及以上的谐波分量较少。同时，三相磁链略有不对称，A相磁链基波幅值略大于B、C两相，这是由于在绕组结构上B相与C相绕组位置相同，而A相绕组不相同，其安装位置居于中间。由此可见，该电机基本没有谐波分量，所以推力波动会非常小。

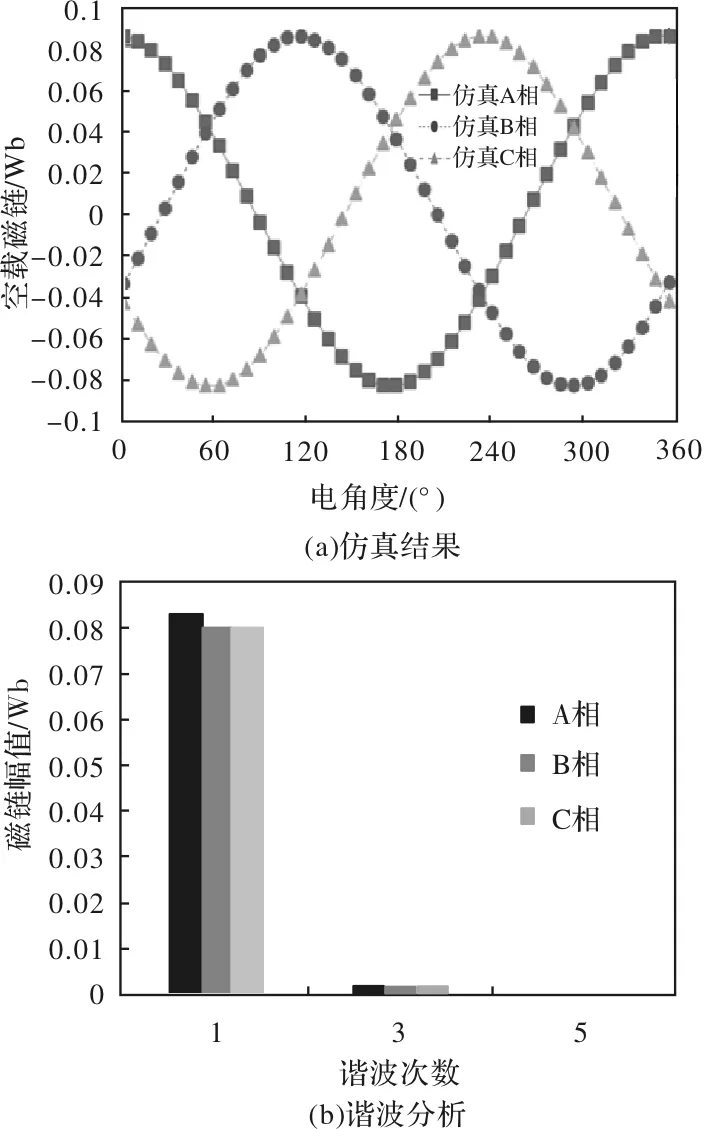
图6 空载磁链仿真结果

4.2 空载反电动势

图7为速度2.02m/s时电机的空载反电动势。为了验证分析结果，图中提供了样机的测试结果，该结果是由图8所示的样机实验平台测得。该实验平台的电机控制器为某公司的STM32303E。

为了清晰地表明结果，图7中将仿真值用实线表示，实测值则只用3种不同形状的点标注。由图中可以看出，三相空载反电动势的仿真值与实测值基本重叠，误差基本可以忽略不计，表明了分析的正确性。

图7 反电动势仿真结果与实测结果

图8 DW-APMLSM样机平台

4.3 电机推力

图9为该电机电枢电流1A时，电机以2.02m/s速度稳定运行时一个电周期内推力曲线的仿真与实测结果。由图可见，平均推力与推力波动的仿真结果分别为18.3N，1.2%，而对应的样机实测结果则分别18.9N，2.7%。从平均推力来看，样机实测值比仿真值大了约3.3%，这可能是由于实际样机气隙长度比设计长度略微偏小引起的。同时，仿真时电机叠厚只按照永磁体叠厚去设计，而样机如图8(a)所示，线圈端部长于永磁体叠厚，该部分端部在磁场的作用下对平均推力有一定的增大作用。推力波动实测值比仿真结果要大，主要原因主要在于测量过程中存在的摩擦力，以及实际样机加工中存在的气隙误差。

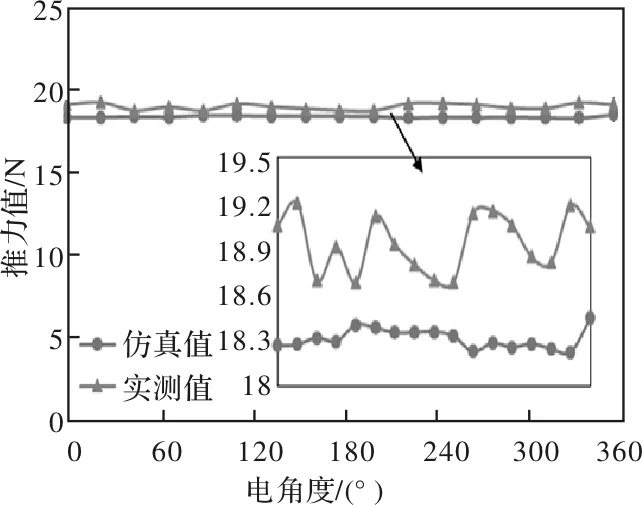
图9 推力仿真结果与实测结果

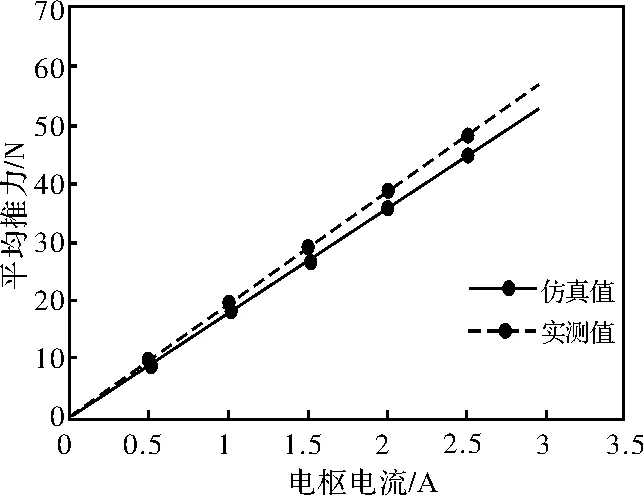
图10 推力-电流曲线仿真结果与实测结果

图10给出了该电机的平均推力-电枢电流曲线仿真结果与实测结果。由于电机初级绕组部分没有铁心，不存在电枢电流增大带来的磁路饱和问题，因此平均推力与电枢电流成正比。图中的仿真曲线和实测曲线都很好地符合了这一点。但是，在电流增大后，实测曲线略微浮高于仿真曲线，即推力实测结果要大于仿真结果，其原因跟前述相同，即实际样机中线圈端部也存在磁场，因此也能够提供一定的平均推力。

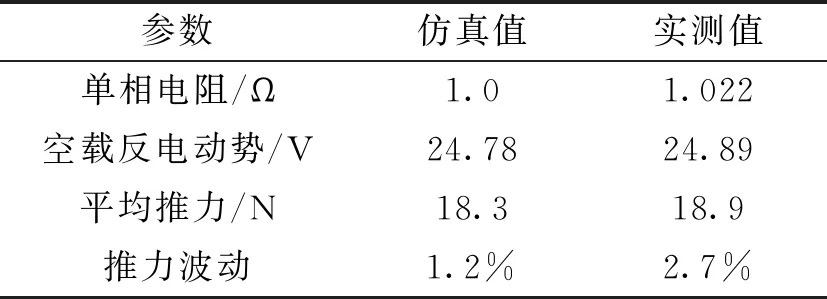
表4 电机性能参数

表4中列出了电阻、空载反电势、平均推力与推力波动的仿真值与测量值。由表中可见，空载反电动势与平均推力误差较小，只有推力波动误差略大。总的来说，测试结果很好地验证了仿真结果，表明了分析结果的正确性。

图11 对比电机模型

为了对比双层绕组与普通集中绕组在电磁推力方面的性能优劣，设计了一个用于对比仿真的单层集中绕组电机模型如图11所示。该模型次级部分与图1所示的模型完全相同，只是将9个双层绕组替换为6个单层集中绕组。为了保证电磁负荷相同，将其单线圈边的截面积固定为

36.3×9/6=54.4 mm

该模型电机仿真得到的平均推力为165N，推力波动为0.68%。其推力密度低于所提出的双层绕组结构。

5 结 语

本文提出了一种新型双层绕组无铁心永磁直线电机(DW-IPMLM)，在确定槽极配合的情况下，针对该种结构进行了优化设计，基于结合考虑最高推力密度与最小推力波动的优化目优化了结构参数，并制作了一台样机，通过样机实验测试验证了仿真结果。由此可以总结得出该种DW-IPMLM的优势在于：

(1)奇数线圈的无铁心永磁直线电机，如线圈数为9，15，21等，都可以根据采用本文提出的双层绕组结构，从而提升推力密度。

(2)奇数线圈的无铁心永磁直线电机，最优槽极配合为槽极数相差3，如9s/6p,15s/12p,21s/18p。

(3)双层绕组由两层绕组叠压而成，每层均为端部非重叠的集中绕组，不仅保留了集中绕组结构简单、加工方便、节约空间的优点，还能够有效提高绕组系数，达到增大推力密度的设计要求。