循环流化床锅炉汽温系统的自抗扰控制

陈德民，顾红艳，张东东，安银敏

(贵州大学 电气工程学院，贵州 贵阳 550025)

循环流化床锅炉(Circulating Fluidized Bed Boiler，CFBB) 具有适应性广、负荷调节性能好、燃烧效率高、环境污染小等优点，在电力生产行业中得到越来越广泛的应用。CFBB蒸汽温度的有效控制对火电机组的安全经济运行具有重要意义。然而，汽温对象具有很大的惯性，且其动态特性会随运行工况发生较大变化[1]，传统的比例积分微分(Proportion Integration Differentiation，PID)控制技术难以获得令人满意的控制效果，对象模型的不确定性又限制了最优控制等现代理论的有效应用。神经网络结构和规模的选取不明确、遗传算法的收敛速度低、模糊规则归纳困难等缺点以及过于复杂的算法和结构使得智能控制目前还难以获得广泛的应用[2-3]。预测控制方法算法繁琐、自适应控制难以在大时间延迟系统中得到应用等缺点，它们目前还不能对工程应用提供有力的支持[4-5]。因此，研究一种简单又不完全依赖系统模型、鲁棒性和适应性强的控制策略，对于提高现有循环流化床锅炉汽温系统的自动化水平有着十分重要的现实意义。

自抗扰控制器(Auto Disturbance Rejection Control, ADRC)是中国科学院韩京清教授提出的一种新型的反馈线性化控制策略。该方法由九十年代初提出的非线性PID控制(Nonlinear Proportion Integration Differentiation，NLPID)策略演化而成。ADRC的核心思想是将系统中的不确定性、模型误差、干扰等作为一个扩张状态，通过观测器进行估计并补偿。利用扩张状态观测器(Extended State Observer,ESO)代替NLPID反馈回路中其中一个用来观测系统实时运动状态的跟踪微分器(Tracking Differentiator，TD)，以实时估计被控对象的扩张状态变量然后利用控制率进行补偿。这种新的非线性状态误差反馈控制律(Nonlinear State Error Feedback，NLSEF)，能够自动补偿对象模型的内扰和外扰。自抗扰控制器大大摆脱了对对象模型的依赖， ADRC内在的鲁棒性使得它可以应用于十分广泛的对象中。

本文针对某300 MW循环流化床锅炉的汽温自抗扰控制系统，采用自抗扰控制器作为汽温串级控制的外环控制器。进行控制器的参数整定，设计系统性能分析实验，研究拥有自抗扰控制器的循环流化床锅炉汽温控制系统的可行性。

1 问题描述

1.1 循环流化床的原理及优点

循环流化床锅炉技术是燃烧化石燃料以及各种生物燃料的燃烧技术。它的基本原理是使燃料在流化态下燃烧。循环流化床锅炉由于独特的设计和运行条件，具有如下优点[6]:

1.燃料的适应性好。循环流化床锅炉既能烧好的燃料，还能烧劣质燃料，十分适合一些燃料种类和质量多变的用户。

2.燃料的燃烧效率高。颗粒与气体间的相对速度很大，有很好的传热效果。而且由于炉内颗粒有内外两个循环，延长了颗粒的停留时间。

3.操作灵活，易于调节。负荷变化后，只要调节给煤量和流化速度，就能满足调节的要求。

4.污染物排放低。将石灰石等脱硫剂加入正在燃烧的循环流化床锅炉中，在900 ℃左右的分级燃烧下产生的还原地带内，便可完成炉内的脱硫与脱氧反应。

5.灰渣的综合治理十分便利。循环流化床锅炉产生的灰渣含碳量很低。这样的低温烧透便于实现灰渣的综合利用。

6.建设和运行费用适当。根据CFBB经济运行及环保问题的费用， 普通锅炉建设及运行费都要高于循环流化床锅炉。

1.2 ADRC的结构和原理

ADRC包括TD，ESO， NLSEF三个主要部分，功能各有不同。TD可以在得到其信号的微分信号的同时将被污染信号转化成光滑信号；ESO对状态变量和未知外扰进行精确的实时估计；NLSEF用非线性的函数进行计算，算出的控制量的最优解对系统进行精确控制。

因此ADRC是基于TD处理参考输入，ESO估计系统状态和总扰动，通过NLSEF进行非线性组合的控制器。

三阶自抗扰控制系统的结构图如图1所示[7]：

图1 三阶自抗扰控制系统的结构Fig.1 The structure of third-order auto disturbance rejection control system

由图1可知，ESO的形式为

(1)

式中：控制信号u和系统输出y为ESO的两个输入，z1、z2和z3为ESO的输出，b0为决定补偿强弱的“补偿因子”，β1、β2和β3为需要确定的观测器参数。

其控制律的形式为

u0=kp(r-z1)-kdz2，

(2)

式中：kp为比例系数，kd为微分系数，r为设定值，u0为误差反馈控制量。

对误差反馈控制量u0，用扰动估计值z3的补偿来决定最终控制量u：

(3)

2 ADRC的整定方法

控制器参数kp、kd、b0，再加上需要确定的观测器参数β1、β2、β3，ADRC需要整定6个参数。整定方法[8]如下：

2.1 控制参数kp和kd的整定

kp和kd决定ADRC系统的预期动态方程

(4)

式中s为复平面的复数。在单位阶跃输入下，为了使系统稳定且不产生震荡，令

(5)

式(4)变为

(6)

故系统的单位阶跃响应为

y(t)=1-(1+ωct)e-ωct，

(7)

根据调节时间定义

|y(ts)-y()|=Δ，

当y()=1,稳定值的误差范围Δ=2%时，可解得

ts=5.85/ωc。

(8)

由于调节时间ts和超调量σ% 是ADRC的主要动态性能指标，为使超调量不受控制带宽ωc影响，恒为0，因此控制器参数的整定任务即选择合适的ωc值，使得系统获得满意的调节时间ts。

系统实际输出难免会跟预期存在一定程度的偏差，因此在选择预期动态参数时需要保留一定裕量，实际设计中令:ts≈10/ωc。

当系统要求的调节时间ts已知时，根据式(8)可获得控制参数ωc，由式(5)计算得到kp和kd，从而决定控制系统的预期动态特性。

2.2 观测器参数β1、β2、β3的整定

观测器参数β1、β2、β3决定观测精度。ADRC控制系统在z3(s) 完全跟踪f(s)的情况下能够获得预期动态特性。z3(s)和f(s) 之间的传递函数为

(9)

由于实际控制过程中，中、低频信号往往较高频信号更为重要，且由于中低频系数(β3和β2)一般要显著大于高频系数(β1和1)，因此可以近似认为式(9)中分母只需保留前两项已经足够描述z3和f之间的传递关系。因此

(10)

其中k=β3/β2，k值越大ESO的观测速度越快。类似2% 调节时间的定义，定义z3跟踪f(s)的滞后时间为Tt，从式(9)可知

Tt≈4/k。

(11)

在设计控制器时，一般要求Tt小于ts，k可以参考被控对象的特性根据式(11)确定。在k值确定的情况下，观测带宽ω0对ESO观测速度的影响较小时，令ω0=4ωc。

为了使观测器ESO在ω0取值较小的情况下仍能获得较好的观测速度，参数的整定为

β1=3ω0,β2=3ω02,β3=kβ2。

(12)

2.3 参数b0的整定

参数b0的作用是稳定控制系统。它的选择是系统响应速度与鲁棒性相互权衡的过程。整定时，先将b0选取一个较大值，将其投入运行。如果系统响应速度太慢，就减小b0，响应太快，就增大b0。

3 循环流化床锅炉汽温自抗扰控制系统

3.1 控制对象

本文重点选取某300 MW循环流化床锅炉汽温控制过程75%和100%的工况[9]进行研究。

75%工况下对象的动态特性为

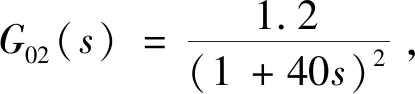
(13)

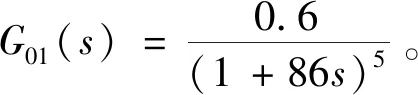
(14)

100%工况下对象的动态特性为

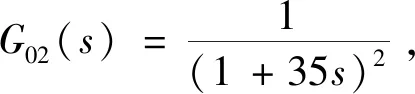
(15)

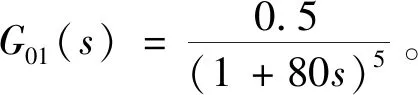
(16)

控制系统结构为双回路汽温系统，对内外回路的参数分别进行整定，内回路采用PI调节器，整定方法运用衰减曲线法；外环路采用自抗扰控制，按照上述自抗扰控制器的整定方法，根据被控对象的动态特性，获取系统的调节时间ts，计算控制带宽ωc和观测带宽ω0，整定ADRC控制参数kp和kd以及观测器参数β1、β2、β3，逐渐增大b0值，直至系统动态性能指标满足系统要求。

3.2 跟踪实验

利用仿真平台Simulink对ADRC-PI汽温控制系统和PI-PI汽温控制系统进行分析。当给定值单位阶跃变化时，观察自抗扰调节系统的跟踪情况。将运行时间设为8000 s时，其单位阶跃响应曲线如图2、图3所示。

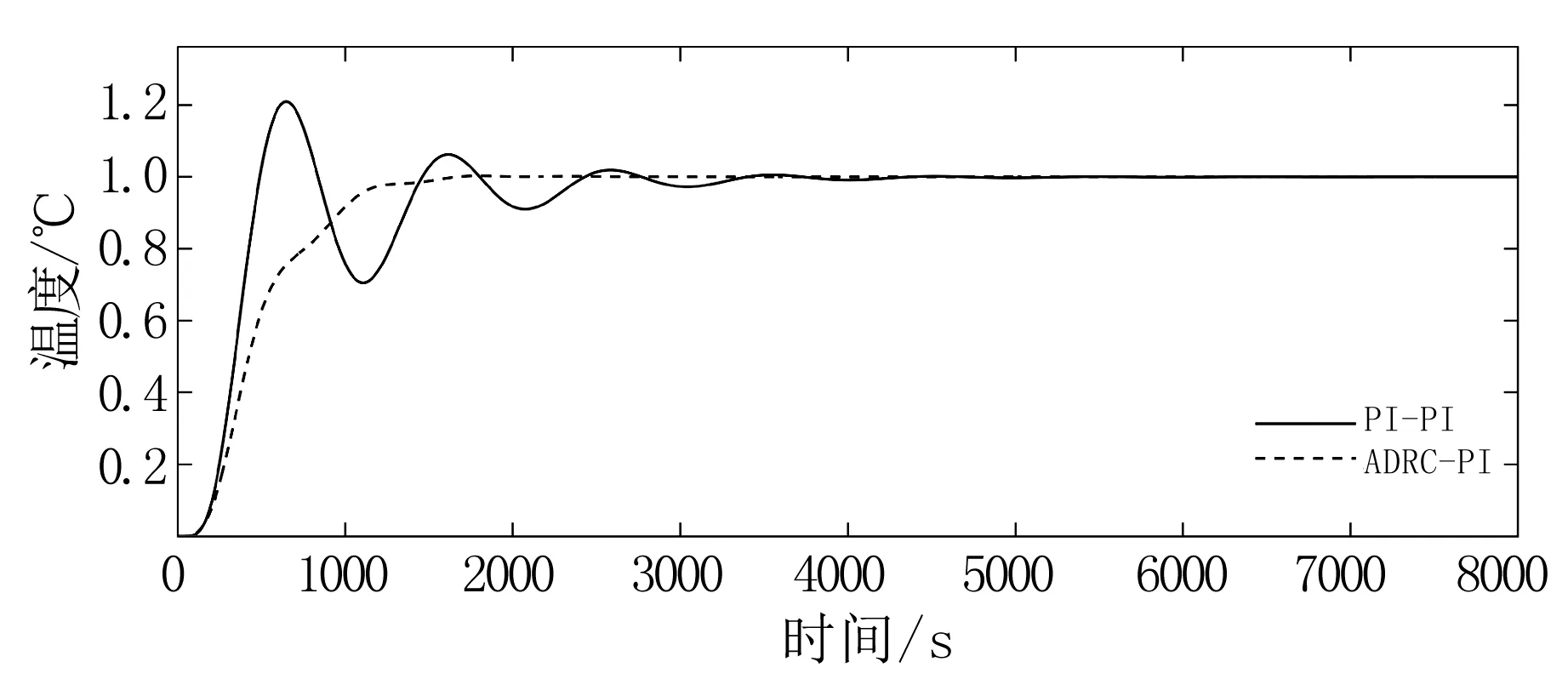
图2 100%负荷时汽温控制系统阶跃响应曲线

Fig.2 Step response curve of the steam temperature control system at 100% load

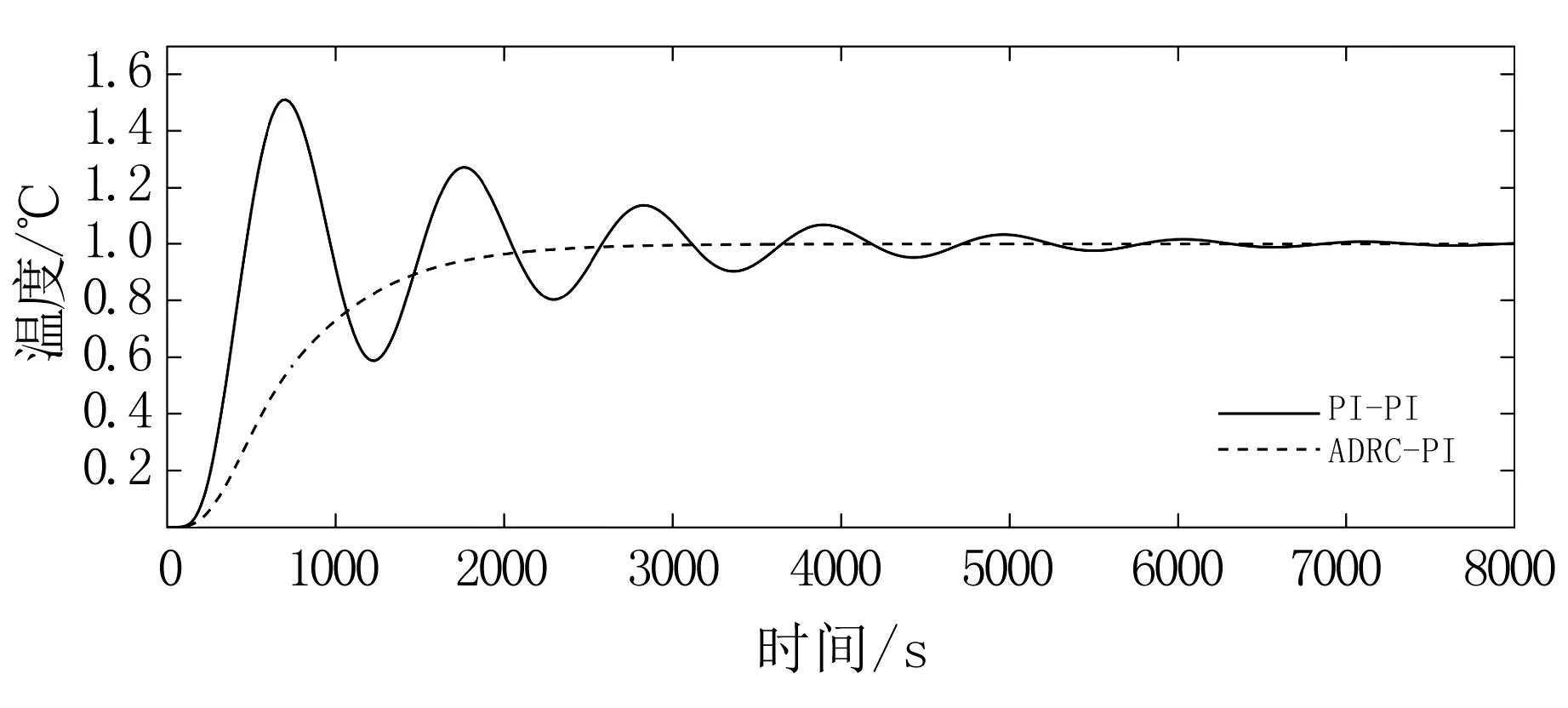
图3 75%负荷时汽温控制系统阶跃响应曲线Fig.3 Step response curve of steam temperature control system at 75% load

由图2可知，PI-PI汽温控制系统的调节时间比ADRC-PI增加1000 s，而且超调量也远高于ADRC-PI。因此，100%负荷时，ADRC-PI汽温控制系统具有更好的控制品质，能够更快达到稳定。

由图3可知，ADRC-PI汽温控制系统的调节时间比PI-PI减少3500 s，相较于PI-PI汽温控制系统高达50%的超调量，ADRC-PI超调量仅为0.01%。这说明ADRC-PI汽温控制系统效果明显优于PI-PI汽温控制系统。

3.3 扰动实验

在汽温控制系统稳定运行的基础上，在其内回路加入一个终值是20，取样时间为1000 s的扰动。观察两种控制系统在有扰动的情况下的输出。

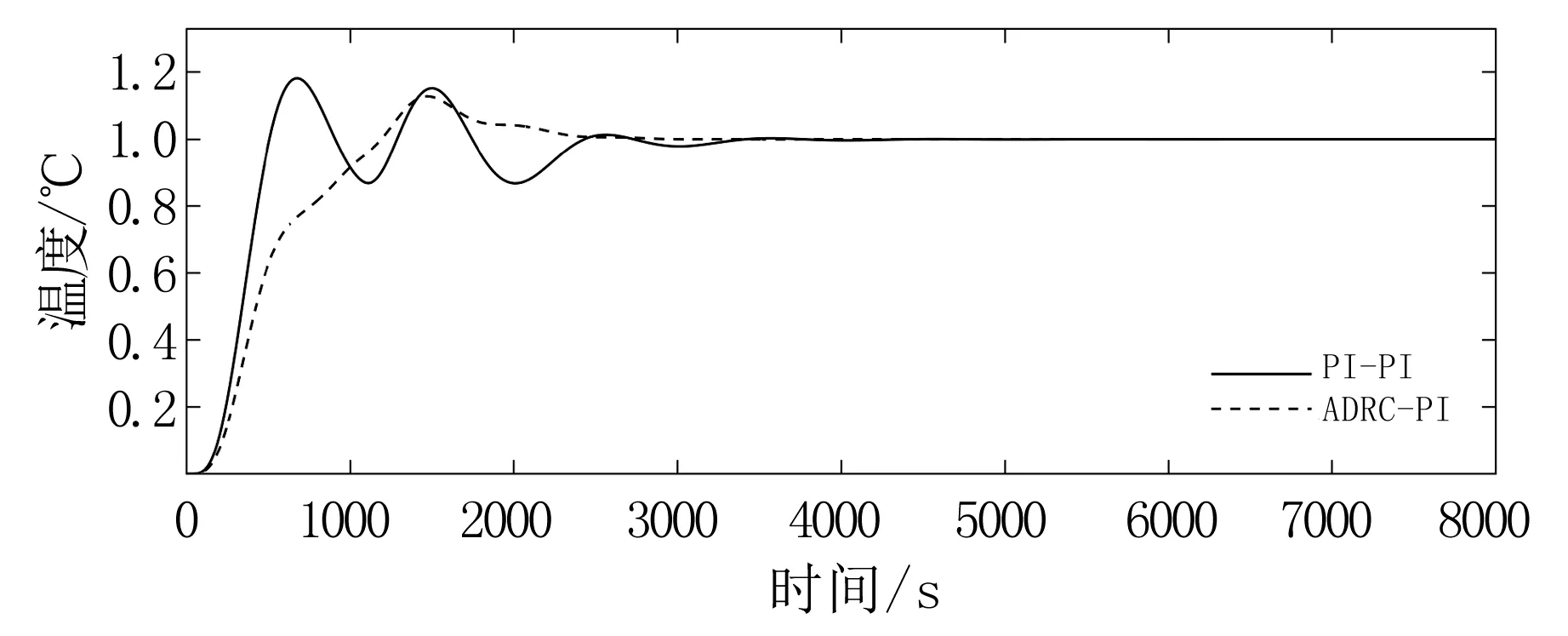
图4 加干扰后系统的响应曲线Fig.4 The response curve of the system after adding interference

由图4可知，PI-PI汽温控制系统的曲线波动多且幅值大，而且调节时间比ADRC-PI增加1500 s。所以就抗干扰能力而言，自抗扰技术有很大的优势。

3.4 鲁棒性实验

在燃烧的实际过程中，对象的实际数学模型会随时间发生变化，无法得到确定的数学模型，存在很大的不确定性，因此对控制系统的鲁棒性有很大的要求。将100%负荷整定出的控制器参数对不同负荷的工作状态进行控制，比较控制效果，如图5、图6所示。

图5 100%负荷时ADRC-PI控制系统在不同工况下响应曲线Fig.5 Response curve of ADRC-PI control system at 100% load under different working conditions

由图5和图6可知，100%负荷下整定的PI-PI汽温控制系统，在25%负荷的工况下无法使系统达到稳定，其余工况的稳定性和快速性也较ADRC-PI差。ADRC-PI汽温控制系统具有较强的鲁棒性，它比PI-PI汽温控制系统能够更快地达到稳定，而且超调量较小。

图6 100%负荷时PI-PI控制系统在不同工况下响应曲线Fig.6 Response curve of PI-PI control system at 100% load under different working conditions

4 结语

本文分别对ADRC-PI汽温控制系统和PI-PI汽温控制系统进行跟踪实验、扰动实验和鲁棒性实验，分析结果表明运用自抗扰控制技术能使循环流化床锅炉汽温控制系统达到更好的控制效果，具有良好的跟踪性及抗扰动的能力，不仅曲线波动少平衡快，而且所需的控制时间短。此外，本文采用新型自抗扰控制器参数整定方法，能够使自抗扰控制更易于实现且具有更广泛的适用性。