基于集中补给-排泄的裂隙水运移模拟试验

张雪梅，丁坚平*，褚学伟,2，令狐燕艳，吕子明

(1.贵州大学 资源与环境工程学院，贵州 贵阳 550025；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610005)

基岩在应力作用下常产生各种裂隙：成岩裂隙、构造裂隙和风化裂隙等[1]。裂隙发育的岩溶区，常存在落水洞的点状集中入渗和泉点的集中排泄的裂隙地下水流[2]。赋存于裂隙中的水是地下水的重要组成部分。随着人类日益增长的物质需求，对地下水资源的开采利用也日益加剧，世界上很多地区如欧洲、亚洲、美国的地下岩溶系统赋存了大量的地下水资源。然而我们对复杂地下含水系统的认识还处在探索阶段。地下裂隙既是地下水资源的储存空间也是地下水的运移通道[3]。探究裂隙中的水流状况对解决水文地质、工程地质及环境地质问题有极大的帮助[4]。与松散沉积物形成的孔隙相比，裂隙在空间分布上具有显著的方向性，各裂隙板间存在较弱的水力联系，且水量分布极不均匀，从而使裂隙水具有强烈的不均匀性、各向异性和随机性[5]。这是导致水流呈非线性的根本原因，从而达西定律的适用性受到限制。

由于地下含水介质的形态、空间分布极其复杂，根据当前的技术手段和勘测设备很难准确测量出其空间位置和几何尺寸。众多研究者便从室内模拟出发，降低研究对象的空间尺度，通过设计室内模型来模拟水流在含水层中的运动[6-8]。ZHANG基于实验室模型以裂隙开度的尺寸为判据来区分裂隙和管道[9]。后来ZHANG又设计了在不同的水文情景下用主控管道和裂隙模拟岩溶含水层的水头变化特征[10]。FAULKNER在室内进行了岩溶含水层地下水流和溶质运移模拟研究[11]。KARAY在室内模拟了裂隙岩体中的地下水流场[12]。

上述试验研究分别从不同的角度对裂隙、管道中水流及溶质运移特性进行模拟和分析，取得很大的进展，但更深入的问题有待进一步研究。如裂隙中水流的运移机理有待进一步完善，裂隙三次方定律在不同条件下的适用性有待进一步研究。为了深入研究裂隙中水流的水动力特征，本文针对不同的裂隙宽度，进行定水头补给条件下的稳定流模拟试验，研究裂隙稳定流中流量与隙宽的关系；进行不同初始水头补给条件下的退水过程模拟试验，分析退水曲线的形状，对退水过程进行非线性拟合。

1 试验模型

试验装置的主要组成部分有：补给系统，裂隙渗流模拟系统，监测系统。装置的主视平面图见图1。

图1 单裂隙渗流室内试验装置简图Fig.1 The sketch of laboratory test device for single fracture flow

补给系统主要由电源、微型潜水泵、循环水箱以及柱型溢流水箱构成，稳定水头主要由溢流孔、调节阀以及微型潜水泵共同控制。

裂隙渗流模拟系统主要由三块隙宽不同的单裂隙板组成，裂隙的裂缝宽度分别为：b1=0.5 mm、b2=1.0 mm、b3=2.0 mm；各裂隙板缝隙的有效延伸长度为110 cm，有效延伸宽度为50 cm；裂隙板上有注水孔、泄水孔以及测压管连接孔。为了便于观察和排除裂隙装置中的气泡，单裂隙板选用两块透明的有机玻璃板组成，采用弹性硅胶管连接裂隙板侧面的管嘴形成测压管，用于监测裂隙装置的测压水头。

监测系统由水头监测与流量监测两部分组成，由于裂隙的尺度比较小，很难安装满足精度要求的自动监测仪，所以外接测压管监测其水头，流量监测采用体积法进行。

2 试验过程

试验中主要观测的水力要素有水头和流量：(1)监测定水头补给时裂隙进口水头、出口水头和出口处稳定流量，(2)监测不同初始水头补给时退水过程的裂隙进口水头、出口水头和出口流量。试验选取与地面水平的平面作为基准面。试验方案及步骤：(1)首先将裂隙进口处的水阀关闭，通过调节补给箱中的溢流孔使箱内水头H0达到指定高度并保持稳定，在本研究中选定的定水头H0分别为190 cm、180 cm、170 cm、160 cm、150 cm、140 cm、130 cm、120 cm、110 cm(溢流水箱标尺标高加试验台标高)共9组。(2)打开裂隙进口处的水阀，使水流流畅地(有时需要排除装置中的空气)通过裂隙，并再次调节溢流水箱中的水头，使其保持在原始的高度。(3)待水箱水头再次稳定后读取裂隙进、出口处的水头h1、h2，同时测量出口处的稳定流量。(4)稳定水头和稳定流量测量后，进行退水过程监测，关闭溢流箱的供水泵，停止供水，随后立即开始监测裂隙进、出口处的水头和出口处的流量，直到水箱和裂隙装置中的水完全排尽后停止试验。(5)按照补给水箱中水头高度由高到低的顺序分别重复步骤(1)-(4)，本试验中共有三块隙宽不同的单裂隙装置，试验共进行了81组(稳定水头测定27组、稳定流量测定27组、退水过程监测27组)。退水过程的试验结果及非线性拟合均以b3为例。

3 试验结果与分析

3.1 试验结果

3.1.1稳定流中裂隙进出口水头

在溢流箱中设置多组定水头(H0)，分别在b1、b2和b3裂隙中进行试验，试验过程中监测单裂隙进、出口处的测压管水头。当供水箱中的补给水头稳定不变时，进、出口处的测压管水头也恒定不变，不同水文情景下的测压管水头如表1所示。随着定水头H0的减小，裂隙进、出口处的恒定水头也随之递减。

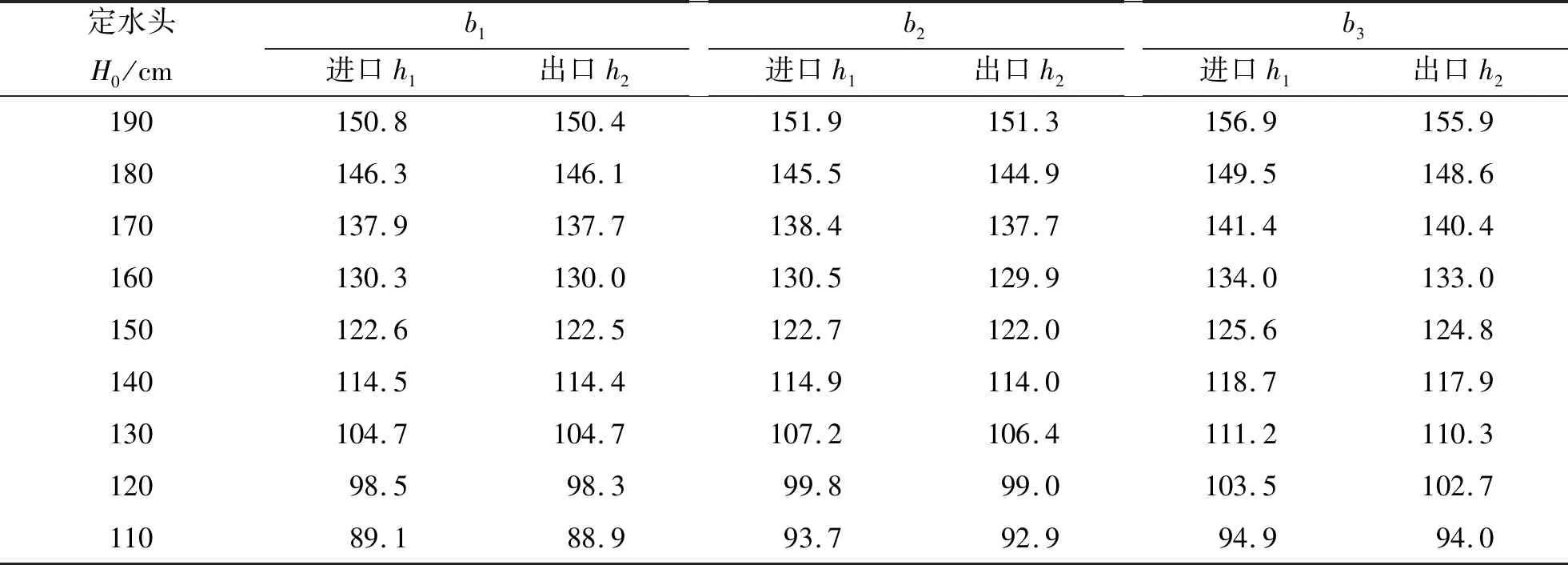
表1 不同隙宽定水头补给的裂隙进、出口水头Tab.1 The steady head at the inlet and outlet of fracture with different gap width and constant supply

3.1.2定水头补给的恒定出流

裂隙的排泄方式采用内径为8 mm的硅胶管连接裂隙排泄孔进行排泄，不同的定水头、隙宽，可得出不同的稳定流量Q。根据各定水头在不同隙宽中的稳定流量数据，作流量柱状图。由图2可知，b1裂隙的流量值与较大两块裂隙的流量相差较大；b2和b3裂隙的流量差值较小，并随着水头H0的减小，两者的流量越接近。

图2 不同隙宽定水头补给裂隙的恒定出流量柱状图Fig.2 The bar graph of steady flow at the outlet of fracture with different gap width and constant supply

3.1.3实测退水过程(水头-时间关系)

分别模拟了b1、b2、b3退水过程的水头-时间关系。根据模拟结果，在给定初始水头的退水过程中，水头-时间过程曲线出现明显的分段现象(图3)，透过裂隙板可见拐点前为饱水的承压过程，拐点后为非承压过程。

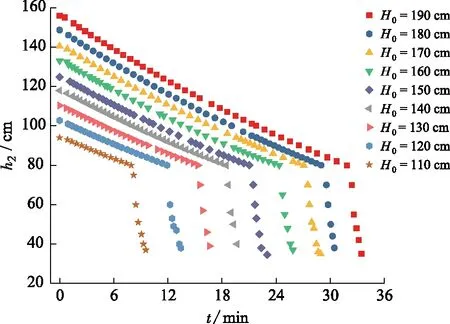
图3 隙宽b3单裂隙出口的实测退水过程(水头-时间)Fig.3 The measured value of single fracture flow recession with b3(h2-t)

3.1.4实测退水过程(流量-时间关系)

由裂隙b1、b2、b3出口处监测其流量衰退过程，结果显示，流量衰退过程也出现分段现象。其中b1裂隙的起退流量随初始水头的递减从0.03571 L/s到0.02259 L/s之间逐级递减；b2裂隙的起退流量随初始水头的递减从0.04327 L/s到0.03018 L/s之间逐级递减；b3裂隙的起退流量随初始水头的递减从0.04885 L/s到0.03108 L/s之间逐级递减。图4为b3的退水过程。

图4 裂隙b3的实测退水过程(流量-时间)Fig.4 The measured value of single fracture flow recession with b3(Q-t)

3.2 结果分析

3.2.1单裂隙稳定出流

三条裂隙的进、出口之间均存在水头差，根据溢流箱定水头的补给，监测不同隙宽裂隙的进、出口实际水头，计算出不同隙宽的水头差，b2与b3裂隙的水头差较明显，b1裂隙的水头差较小。

由图5可见，b1裂隙的水头差仅为2 mm，和b2、b3裂隙分别相差了5 mm和7 mm。由此可推测隙宽越大能量损失越大。

图5 不同隙宽进、出口水头差柱状图Fig.5 The head difference bar graph of inlet and outlet under different gap width

根据单裂隙渗流的三次方定律公式[3]：

(1)

式中：q为单宽流量，m2/s；b为裂隙缝隙宽度，m；ΔH为裂隙水头差，m；L为裂隙长度，m；ρ为流体密度，kg/m3；g为重力加速度，m/s2；μ为动力粘滞系数，N·s/m2。

已知流体的密度和重力加速度，试验过程中的平均温度为25 ℃，查表得动力粘度值[13]，将不同的隙宽值以及水力梯度代入式(1)，计算发现不同隙宽下的裂隙渗流单宽流量与实测流量相差很大。如隙宽为2 mm单裂隙的实测单宽流量为2.0×10-2m2/s，而根据三次方定律求出的单宽流量才6.6×10-5m2/s，两者相差了几百倍，三次方定律远远低估了该模型的渗流通量。周志芳(2007年)也曾提到：三次方定律仅近似地描述两侧壁光滑平直，张开度较大且无充填物的渗流规律，只有当光滑平直单裂隙中的水流呈层流状态时，才满足线性立方定律[3]。

对该裂隙模型的实测稳定流量进行拟合，得出流量是关于隙宽的二次多项式。

Q=A1b2+A2b+A3。

(2)

式中：Q为裂隙出口处流量，L/s；b为隙宽，mm；A1为二次项系数；A2为一次项系数；A3为常数项系数。

在每一个稳定补给(H0)条件下，分别测定b1、b2、b3的稳定流大小，把所测的流量值和隙宽代入(2)式，可列出3个关于A1,A2,A3的线性方程，通过求线性方程组的解可得出一组系数值，则不同的定水头(H0)对应着不同的A1,A2,A3,根据不同隙宽在不同定水头下的实测流量，便可求出一系列的系数组合。根据若干个定水头的实测流量，可拟合出一系列的A1，A2，A3，由此可作出各系数关于定水头的曲线(图6，7，8)。所以当隙宽b已知时，把定水头代入图中便可查得A1，A2，A3，将A1，A2，A3代入式(2)便可求得不同隙宽下的流量。该方法可用于不同补给条件的泉流量估算。

3.2.2退水过程的拐点分析

TANG的研究用主控管道和裂隙对岩溶泉退水曲线进行实验室模拟分析[14]，本文退水过程与TANG的试验结果存在相似之处，即退水过程也分为两个部分，但与TANG不同的是本文试验的整个退水过程发生在闭合裂隙内，裂隙渗流的退水过程明显地分为两个阶段并存在明显的拐点：补给水头较高时，裂隙完全被水充满，裂隙水呈承压状态，此过程即为承压阶段；随着水头的降低，透过有机玻璃明显可见裂隙中进入空气而呈非承压状态，此过程即为非承压阶段。承压阶段裂隙进、出口水头以及出口流量衰退缓慢、平稳，历时长(图3、图4)；非承压阶段裂隙进、出口水头迅速下降，历时短，裂隙中的水很快排泄完，出口流量先呈股状出流、再呈线状、最后以水滴的形式排尽。根据实测退水过程便可求得不同隙宽的临界水头和临界流量。已知排泄管的内径，可计算出每个裂隙的临界流速。经计算得出本试验三个不同尺寸裂隙的各临界值如表2所示。各裂隙的进口临界水头比出口处大，随着隙宽的增大，临界水头、流量、流速随之增大。

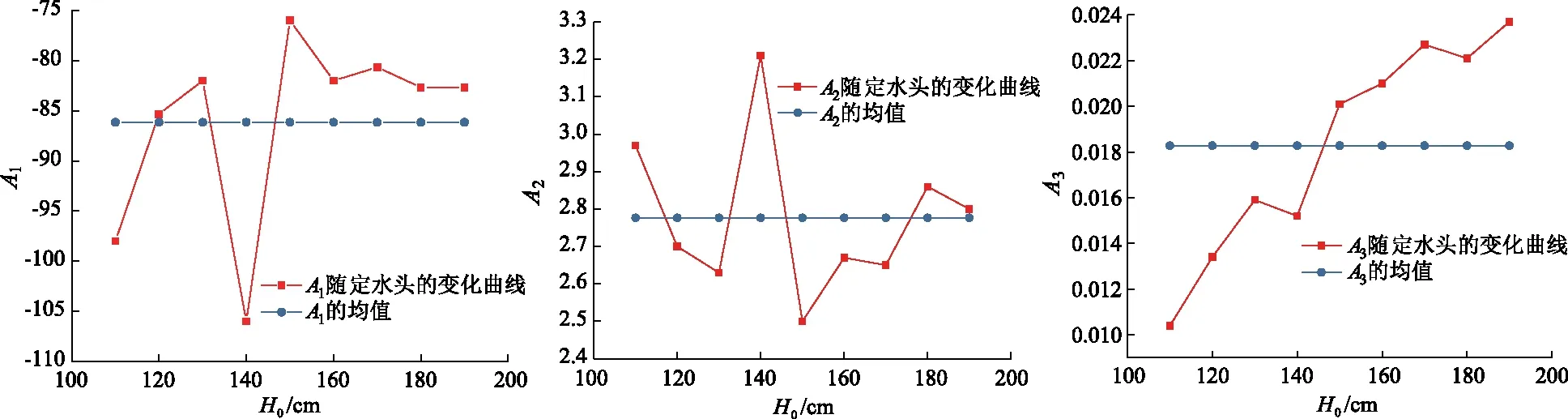
图6 二次项系数 图7 一次项系数 图8 常数项Fig.6 The quadratic coefficient Fig.7 The first-degree coefficient Fig.8 The constant term

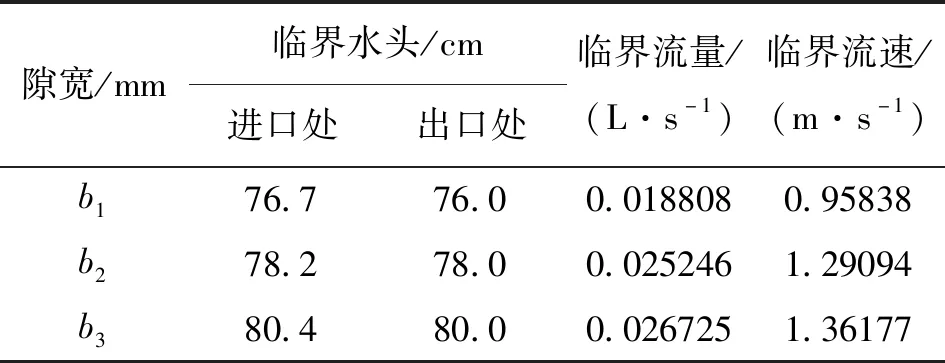
表2 不同裂隙的临界水力要素Tab.2 The critical hydraulic elements of different fractures

3.2.3退水过程非线性拟合

根据试验结果知退水过程分为两个阶段，第二阶段的水头、流量衰退迅速，历时短，监测点数少。从时间尺度上裂隙排泄过程主要由承压阶段控制。该研究对实测退水过程承压阶段的退水规律分别进行了指数曲线拟合与多项式拟合。

1)退水过程指数拟合

由退水过程的实测数据，针对不同裂隙宽度和不同初始水头进行退水过程的指数拟合。拟合曲线见图9和图10，退水过程中的水头衰退规律和流量衰退规律基本符合指数衰退曲线的变化趋势，其中水头拟合的相关性系数为0.99961，流量拟合的相关性系数为0.92286。对不同裂隙宽度和不同初始水头，水头衰退过程和流量衰退过程与指数曲线均有良好的相关性，水头拟合中的相关性系数均值达0.99以上，流量拟合达0.95以上。

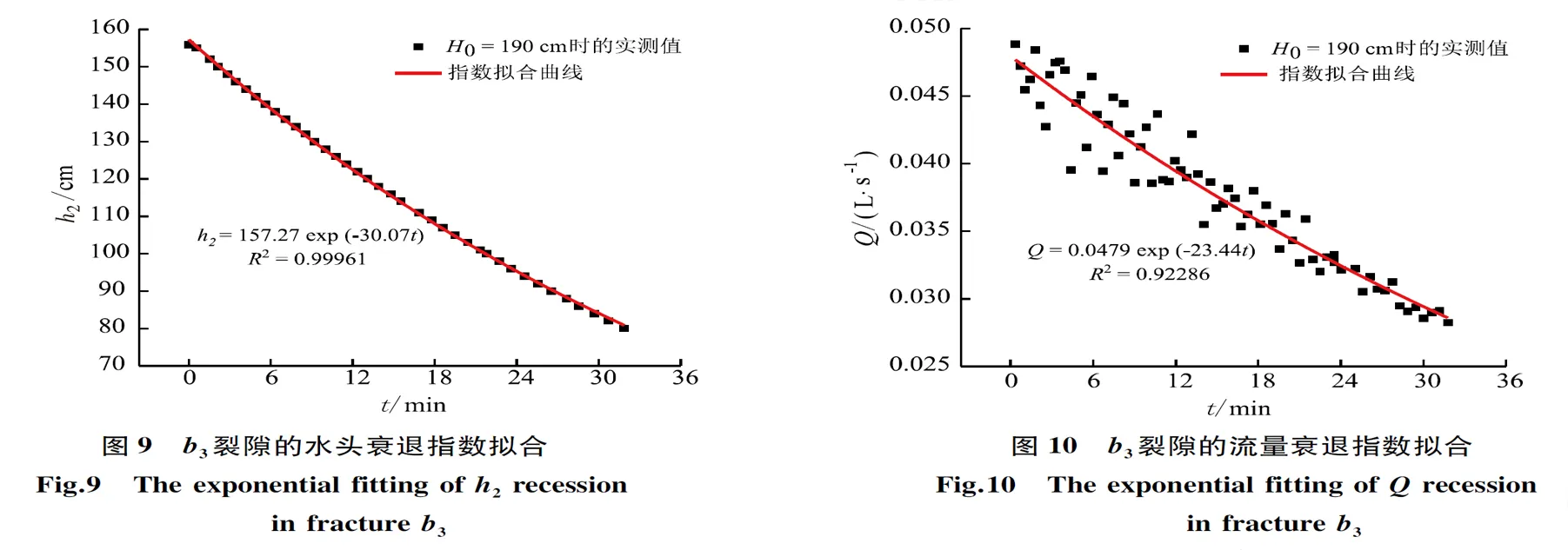
退水过程水头衰退指数拟合满足

h2=h0exp(at)，

(3)

式中：h2为任意时刻的水头，cm；t为时间，s；h0为初始水头，cm；a为指数衰退系数，1/s。

退水过程流量衰退指数拟合满足

Q=Q0exp(at)，

(4)

式中：Q为任意时刻的流量，m3/s；Q0为初始流量，m3/s。

2)退水过程多项式拟合

由退水过程的实测数据进行多项式拟合，如图11和12所示。

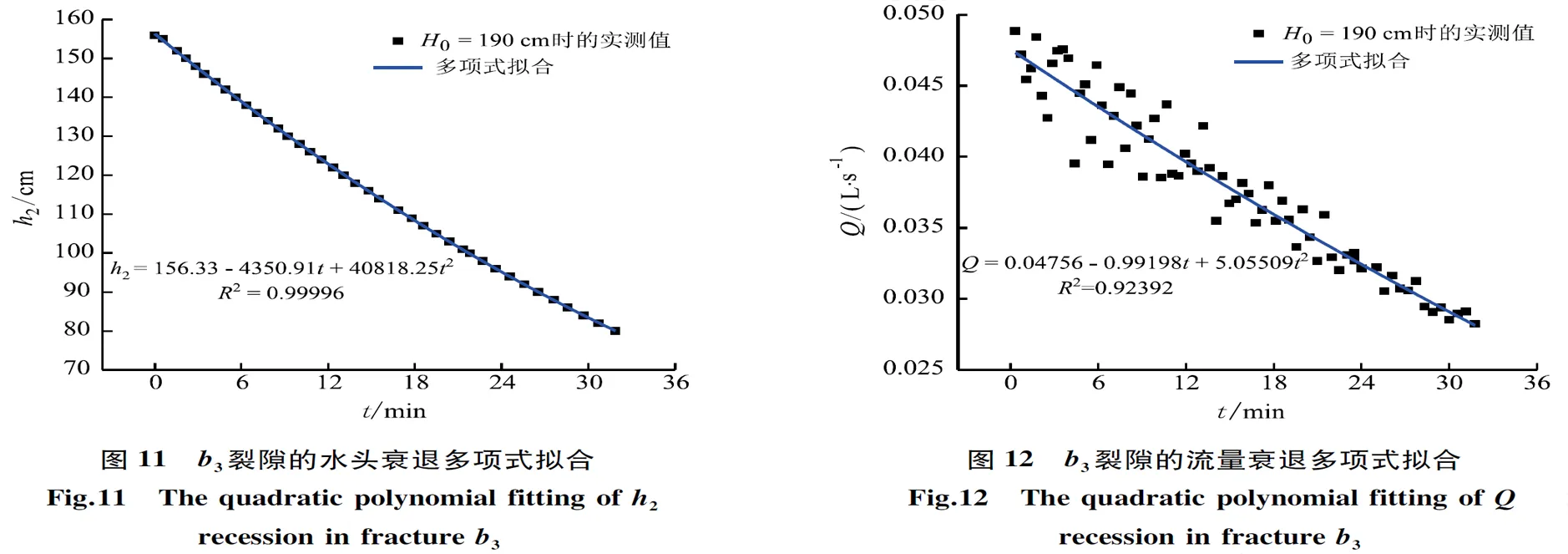
如图所示水头的多项式拟合相关性系数为0.99996，比指数拟合的相关性更强；流量的多项式拟合相关性系数为0.92392，同样优于指数拟合的结果。

退水过程水头衰退多项式拟合满足

h2=h0+Bt+Ct2，

(5)

式中：B为一次项系数，C为二次项系数。

退水过程流量衰退多项式拟合满足

Q=Q0+Bt+Ct2。

(6)

由多项式拟合知当初始水头为190 cm时：水头衰退的多项式拟合方程为H=40818t2-4350.9t+156.33，常数项为156.33 cm，与实测值155.9 cm之间的相对误差仅为0.276%；流量衰退方程为Q=5.0551t2- 0.992t+ 0.0476，常数项为0.0476 L/s，与实测值0.0489 L/s之间的相对误差为2.658%。

3)退水过程拟合相关性分析

对比指数拟合与多项式拟合的相关性如图13所示。

图13 退水过程拟合相关性分析Fig.13 The correlation analysis of recession fitting

水头和流量的拟合均有较好的相关性，但水头拟合的相关性较流量更好，其相关性系数基本没波动，保持在0.99左右。流量拟合的相关性系数较小且波动较大，经分析得出最大的误差来源是采用体积法测流在操作过程中产生了误差，对结果造成了一定影响。

3.2.4裂隙衰退系数

本文试验的指数拟合结果类似于布西涅斯克在泉流量和含水层排泄机理理论研究中对水流扩散方程求得的近似解析解[15]。

Qt=Q0exp(-at)，

(5)

式中：Qt为t时刻的流量，m3/s。

根据退水过程的流量拟合，不同隙宽的单裂隙流量衰退系数变化情况如图14所示，衰退系数均在21-29之间变化，并且随着隙宽的增大，衰退系数也随之增大；同时当初始水头发生变化时，衰退系数也相应变化，其变化趋势为：初始水头的大小与衰退系数呈负相关关系。由此表明大裂隙中水流衰退的速率快，初始水头较高时，水流衰退速率反而变慢。

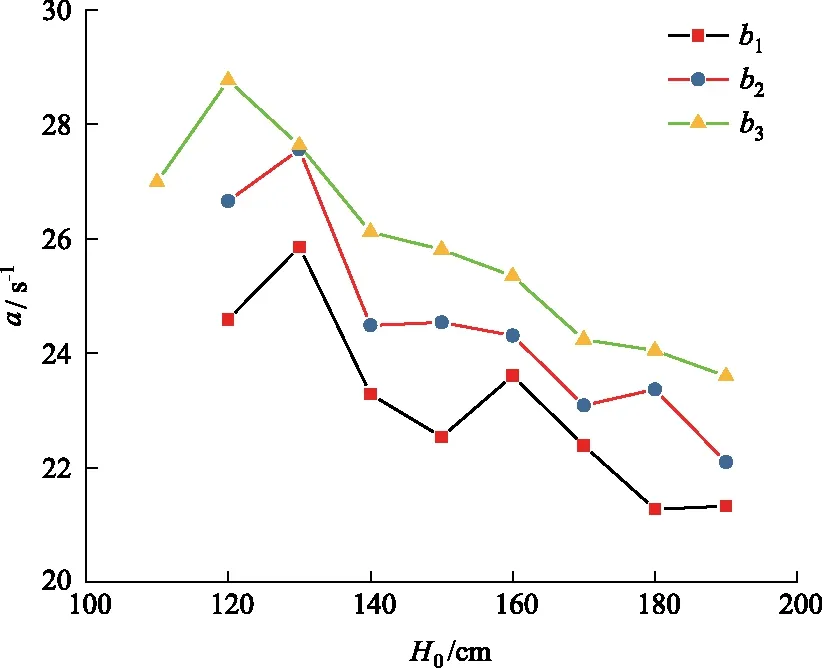
图14 衰退系数分布曲线Fig.14 The distribution curve of recession coefficients

4 结论

根据试验结果及其分析主要得出以下几点结论。(1)在稳定流试验中，隙宽越大，裂隙进、出口水头差越大，稳定流的流量同隙宽之间有很好的二次多项式关系。(2)退水过程分为两个阶段，分别为承压阶段和非承压阶段。(3)对裂隙的退水过程同时进行指数拟合和多项式拟合，多项式的拟合较指数拟合精度高，相关性较好；在不同的补给条件下，不同隙宽中水头衰退拟合出的初始水头与实测值的误差均小于1%，流量衰退拟合出的初始流量与实测值的误差均小于10%，该结论可应用于泉流量的估算；少有学者对泉流量及裂隙流的退水过程进行多项式拟合，该方法对研究不同补给条件下裂隙流规律有参考意义。