基于局部Fisher准则判别投影的人脸识别算法*

任克强, 张静然

(江西理工大学 信息工程学院，江西 赣州 341000)

0 引 言

在自动人脸识别过程中，如何高效的将原人脸图像空间中数据映射到低维空间中是一个关键问题，特征降维不仅可以使原数据变换后有特定属性，而且可以提高计算的效率。子空间作为一种有效的降维和特征提取方法在人脸识别领域有广泛应用[1]。

线性子空间降维方法有基于主成分分析(principle component analysis，PCA)[2]、线性判别分析(linear discriminant analysis，LDA)及二维的2DPCA和2DLDA等方法，但以欧氏结构来衡量样本点间相似性难以挖掘数据本征的特征，导致传统的线性子空间算法很难对数据在低维空间的分布做合理的估计。近年来流形学习领域产生的大量研究成果表明人脸图像数据呈现非线性结构，且可能取样于嵌入在高维欧氏空间的低维流形子空间中，很难利用全局线性映射来寻求这种低维投影。以不同准则来对数据进行降维的流形学习算法尝试揭示数据的本征分布结构，这种非线性降维方式直观有效，目前在人脸识别方向基于流形的子空间算法有局部保持投影(locality preserving projection，LPP)[3]以及对称局部保持的半监督维数约简[4]等。但为了更加有效的利用样本标签信息进行样本的分类，研究者们提出了监督的判别流形学习算法，如监督拉普拉斯特征图[5]、多邻域保持嵌入[6]等，在保持样本局部信息的同时，提升由样本类别信息带来的判别能力。以上降维约简技术从样本中提取有较好判别性的子特征，但对噪声和有损信号的应对能力不理想，而稀疏表示则对有损信号有较好的建模能力。文献[7]借鉴LPP的局部嵌入思想以保持数据的稀疏l1图结构，编码阶段先根据以训练样本作为字典学习稀疏系数，然后投影保持这种稀疏关系；识别阶段直接将测试样本由学到的投影矩阵投影到低维子空间，用最近邻识别器分类。文献[7]能够较好地提取保持数据间稀疏特性的特征，但没有合理利用样本标签信息；文献[8]在此基础上考虑稀疏结构投影保持的同时，利用样本标签信息来提升特征判别能力及降低算法复杂度。文献[9]在样本标签信息可利用情况下保持数据的稀疏l1图结构，最终转化为回归问题求解投影矩阵。文献[10]在获取数据特征表示的同时保持变换后的样本关系，可以提取利于子空间分类的稀疏的近邻结构。

针对近邻图中通过实验方法选择近邻参数K不能完全反映数据真实近邻分布的问题，本文提出局部Fisher准则判别投影算法，通过求解样本在总体样本下稀疏表示来自适应选择样本的近邻参数，以使样本间分布关系尽可能符合真实情况，在此基础上利用样本标签信息构造自定义的类内局部散度矩阵和类间局部散度矩阵，以提高样本标签信息带来的判别能力。

1 局部Fisher判别投影

局部保持算法的识别效果很大程度依赖近邻图中参数K的选择，实际应用要进行大量实验来选择最优参数，而且对于分类任务而言，首要目标是设法让不同类的样本有区分度。针对这些问题，本文提出局部Fisher准则判别投影算法。

1.1 近邻矩阵的稀疏构造

通过实验来选择近邻矩阵中近邻尺寸K的大小相当的耗时，而且以欧氏距离作为样本点间相似性度量，是建立在样本相互独立的基础上，实际上会忽略不同样本间的联系性。所有的样本都使用人工选择的固定K近邻参数，实际应用中不合理，也不能真正的反应样本流形结构，如果从邻接矩阵中元素稀疏的角度考虑，可以运用稀疏表示来获取邻接矩阵，使得样本点的近邻结构非固定大小。

(1)

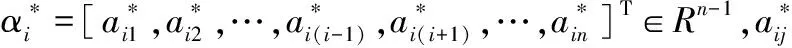
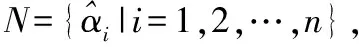
(2)

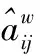
1.2 局部散度矩阵

如果同类样本在低维子空间中分布聚集，而不同类样本在低维子空间中分布分散，那么分类算法构造的分类超平面具有更强的泛化能力，而且有更优的分类性能。

为保证样本xi与同类近邻样本在降维后仍然保持近邻关系，可以考虑减小样本xi与同类邻域矩阵中样本的平均距离来实现，该距离表示为

(3)

式中X′为全体样本集合构成的矩阵

X′=[x1,x2,…,xn]∈Rm×n

由此构造类内局部散度矩阵为

(4)

本文不是按每个样本等权值的方式来构造类内散度矩阵，而是根据信号稀疏表示后的重构系数，即使是同类样本信号它们间也有不同的相似性，利用这种稀疏关系来构造类内散度矩阵可以更优的逼近样本的真实分布。

样本xi与近邻矩阵中不同类样xj(li≠lj,j=1,2,…,n)本间平均距离为

(5)

为了有更优的分类特性，类间散度分布应尽量的大，可以考虑增大降维后的不同类样本点间的稀疏近邻距离。由不同类样本的稀疏近邻关系构造类间散度矩阵为

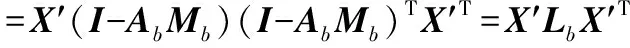
(6)

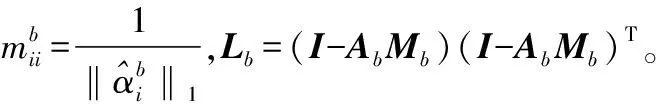
一般将每个近邻图上的样本视作嵌入在同一个子流形上，这样两个非同类的近邻样本就可能位于同一子流形，直接采取保持局部近邻关系的投影算法会导致样本在低维子空间重叠的现象。用于分类的降维投影算法应考虑将处于同一子流形上非同类样本进行相互分离。

(7)

式中μ为均衡因子，0<μ<1。

同时需考虑投影降维后局部的近邻结构得到保持

(8)

为防止投影方向的幅值随意变化而影响求解，可以添加如下正交投影限制条件

WTW=Id×d

(9)

因此,本文局部Fisher准则判别投影的目标函数表示为

γWTX′LX′TW),s.t.WTW=I

(10)

式中γ为均衡因子，用来平衡局部判别项和局部近邻结构保持项的重要性，其中γ>0。式(16)的约束问题可以转化为Lagrange乘子法进行求解

γwTX′LX′Tw-λwTw=wTX′(μ(Lw+Lb)-Lb+γL)X′Tw-λwTw

(11)

Lagrange乘子法最优解的充要条件需满足

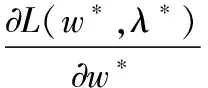
X′(μ(Lw+Lb)-Lb+γL)X′Tw*=λ*w*

(12)

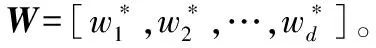
本文局部Fisher准则判别投影算法的步骤描述如下：

S1：PCA降维。通常训练样本的个数远小于样本的维数，为保证应用稀疏表示求稀疏近邻关系时，由训练样本组成的字典超完备，需运用PCA算法将原始样本投影到低维子空间中。

S2：利用式(1)求每个样本的稀疏近邻权值矩阵A，再利用式(2)分别求取同类样本近邻权值矩阵Aw和非同样本近邻权值矩阵Ab。

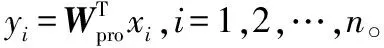
2 实验结果与分析

本文在Yale、AR、Yale B三个公共人脸数据库上进行实验，其中从AR库中选取由50个男性和50个女性组成的共1 400幅只有光照和表情变化的图像子集进行测试。每幅图像剪裁成32×32的尺寸。

为评估本文算法的识别效果，实验将本文算法与PCA，LDA，LPP和文献[9]的DSLFDA以及文献[10]的OSSPP算法进行比较，在Yale，AR及Yale B人脸数据库上，分别测试这些子空间算法在不同训练集和不同降维特征维数下的识别率，图像空间中的二维图像展开表示为1 024维的向量，以便训练获得特征子空间，在实施其它子空间算法来提取特征之前需先应用PCA来预处理数据，且均采用最近邻(nearest neighbor,NN)分类器来进行分类。

2.1 不同特征维数的算法性能比较

本节实验主要分析比较不同降维子空间维数对人脸识别率的影响。实验在Yale数据库上按每人6幅图像来训练，在PCA降维阶段选择特征降维的维数为89，各子空间算法的人脸识别率随维数变化的曲线如图1(a)所示；在AR数据库中按每人7幅图像来训练，PCA降维阶段选择特征降维的维数为200，各子空间算法的人脸识别率随维数变化的曲线如图1(b)所示；在Yale B数据库上按每人32幅来训练，PCA降维阶段选择特征降维的维数为200，不同子空间算法的人脸识别率随特征维数变化曲线如图1(c)所示。

图1 不同维数下的识别率

由图1可知本文算法随着所提取的样本子空间特征维数的增多，人脸识别率开始增长较快，后来慢慢趋于平稳；在图1(a)中Yale数据库上由于训练集样本较少，子空间算法的识别率都没有超过85 %，本文算法有稍优于其它算法的识别性能；而在图1(b)的AR数据库和图1(c)的Yale B数据库上本文算法则有明显优于其他算法的表现。

2.2 不同训练样本个数的算法性能比较

本节实验主要分析比较不同训练样本个数对人脸识别率的影响。实验在Yale数据库中每人随机选取l(l=4,5,6)幅图像用于训练，剩余11-l幅图像用于测试；AR数据库中每个人的14幅图像，随机选取l(l=3,5,7)幅图像用于训练，剩余14-l幅图形用于测试；Yale B数据库中每个人随机选取l(l=10,20,32)幅图像用于训练，剩余的图像用于测试。重复20次实验，取实验平均结果。

在Yale、AR、Yale B这3个数据库上进行不同的训练样本数量对最终识别率的实验，结果如表1、表2和表3所示，表中数据组织为“均值±标准差(维数)”，Baseline为用1024维的人脸数据进行最近邻分类。

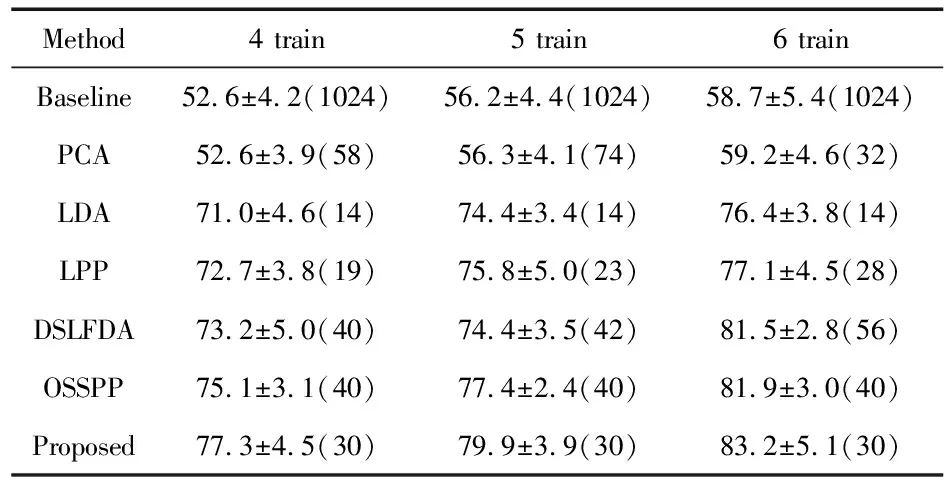
表1 算法识别性能比较(Yale)

从表1结果可知，在小型数据库Yale上，样本数量较少，姿态和光照变化等因素的影响会较明显，所以LDA与PCA的识别率都不理想；相较于DSLFDA和OSSPP，本文算法在考虑稀疏近邻结构的同时，提升了由标签到来的判别能力，能提取信号判别特征，最终计算的子空间有最优的识别率。

表2 算法识别性能比较(AR)

表3 算法识别性能比较(Yale B)

从表2结果可知，在AR数据库上，实验集上的人脸图像信号受身份外的因素影响较小，在训练样本充足时，除PCA之外，具有判别特征提取能力的算法识别率均有提升，但本文算法考虑保持稀疏的近邻结构同时，添加全局类别差异，有优于其它算法的性能。

从表3所示，由于数据库中某些图片的光照因素引起的变化比图片类别变化都要剧烈，所以，PCA在寻求数据最大方差变化方向时极有可能求得由光照引起变化的特征方向，这不利于对图像样本的身份识别，所以，PCA在该样本大的数据库中反而识别效果较差；LDA、LPP直接从原样本中提取具有判别特性的特征，识别性能较PCA有较大提升，但还是较易受光照等因素的干扰；样本足够时，DSLFDA、OSSPP以及本文算法有更高的识别率，且本文算法有更优的识别性能。

3 结束语

本文算法使得同类样本在低维线性子空间中分布聚集，而非同类样本在低维线性子空间中分布分散，以保证最终分类超平面拥有更强的泛化能力。在与相关文献的算法仿真比较实验中，本文算法表现出了更加优异的人脸识别性能，可以有效提升人脸识别率。