SUV汽车悬架下摆臂有限元分析及结构优化

马修文，郑银环，耿 娟，赵 燕

(武汉理工大学 机电工程学院，湖北 武汉 430070)

下摆臂是悬架中重要的导向机构，起传递力和力矩的作用，并保证车轮按照一定运动规律运动，保证车辆的安全平稳行驶，以及整车的操纵稳定性能。在国内早有学者对悬架系统进行分析，黄向东等[1]首先用有限元方法模拟悬架的弹性运动特性并针对麦弗逊等3种悬架建立有限元模型，为悬架建模和有限元分析奠定了基础。朱文学等[2]对前悬架和副车架建立有限元模型，选取6种危险工况获取最大应力位置及数值，进行实车测试，并比较两者的差异。张海波等[3]应用逆向工程技术对其进行逆向建模，应用ANSYS 分析软件对控制臂进行强度分析。

国外研究人员运用有限元法对悬架下摆臂进行轻量化设计，采用拓扑优化和形状优化方法寻求下摆臂最优结构。Banitalebi[4]对悬架下摆臂进行了振动及受力分析，并采用MATLAB和遗传算法对悬架系统进行优化。Kim等[5]提出了一种基于拓扑优化的悬架合成方法，使用由非线性杆和零长度弹簧构成的三维模型，将杆横截面和弹簧刚度值作为设计变量，杆元件的节点位置作为形状优化变量，同时优化拓扑和形状。与国外相比，国内早期轻量化方法主要运用在汽车车架的研究上。范文杰等[6]对车架实现轻量化，既能满足车架的刚度要求，保证汽车的安全性，又能减轻汽车的重量。张兰春等[7]以静态多工况下刚度和动态特征值作为性能指标，构建多目标连续体结构拓扑优化数学模型，进行悬架多目标优化。肖光育等[8]研究了基于静态强度特性的轻量化。扶原放等[9]进行多工况条件下的悬架下摆臂轻量化。张志飞等[10]充分考虑多个优化目标，将单目标拓扑优化形成的子序列与各个目标最优值形成的最优序列进行灰色综合关联分析，并用折衷规划法进行多目标拓扑优化，根据优化结果对控制臂进行改进设计。上官文斌等[11]在建立下摆臂有限元模型的同时也建立了与之相连的球铰和衬套的有限元模型，再对其进行拓扑优化。

综上所述，在对悬架下摆臂进行优化设计时，往往只研究一种性能指标，利用这样的研究结果来评价结构显得太过片面；也有针对多个工况中的每个工况分别进行拓扑优化，但没有综合考虑各个工况在结构设计中的重要程度及影响大小。因此，笔者综合考虑下摆臂的静态和动态特性，基于麦弗逊前悬架系统，在保证这些性能的基础上对悬架下摆臂进行有限元分析与结构优化，使整车性能得到改善。

1 SUV悬架下摆臂结构有限元分析

以SUV汽车通常使用的麦弗逊前悬架系统为研究对象，如图1所示。在CATIA中建立下摆臂结构的几何模型，将下摆臂结构分为上板、下板、球铰座、前后衬套以及前后套管7个部分，然后将这几个部分的几何模型逐个导入Hypermesh中。利用Hyperworks软件进行下摆臂的有限元分析和后续的拓扑优化及尺寸优化，采用Hypermesh、OptiStruct和Hyperview等进行分析和优化。

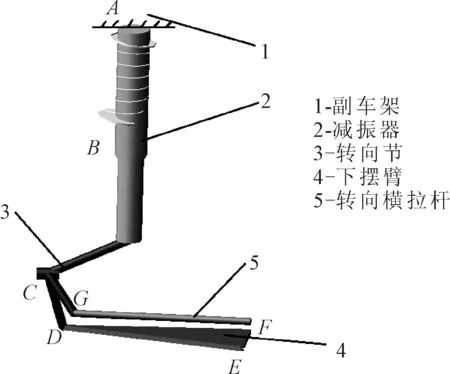
图1 悬架系统机构简图

对悬架系统进行仿真时，还需要部分整车参数，如表1所示。

表1 建模所需部分整车参数

1.1 有限元建模

由于上下板的厚度远小于其长度和宽度，故采用2D单元网格划分方式，在中面上划分网格。对于与上下板都有连接关系的球铰座，形状厚度比较均匀，采用四面体网格划分。上下板的前后套管也属于实体网格划分范围，由于结构形状规则，故选择六面体网格划分。

下摆臂与转向节之间通过球铰相连，与副车架之间通过衬套连接，利用Hypermesh中的1D连接单元(Rigids/RBE2)来模拟。下摆臂的上板和下板之间的连接，球铰座与上下板间的螺栓连接以及衬套安装底座与上下板的连接均采用此刚性连接单元来模拟。下摇臂的有限元模型如图2所示。

图2 下摆臂的有限元模型

该悬架下摆臂的材料名称为SAPH440，其弹性模量E=210 000 MPa、泊松比μ=0.3，屈服极限σ0.2=305 MPa，密度ρ=7.85 g/cm3。对其添加属性材料为Optistruct中的各向同性材料MAT1。

对于下摆臂载荷的提取，首先求得悬架系统在各种典型极限工况下的轮胎接地力，轮胎接地力可以通过经验公式计算得到，再以轮胎接地力作为输入条件，在ADAMS中对系统进行静载仿真，由仿真结果提取下摆臂连接点处的载荷。此方法针对悬架系统更容易实现，利用仿真得到的载荷更加可靠。

选定汽车坐标系如下：X轴正方向是由车头指向车尾，Y轴正方向是从主驾驶位置指向副驾驶的方向，Z轴正方向指向汽车正上方。在文中下摆臂前后点都与副车架相连，约束前点的X、Y、Z轴方向的移动和绕Y、Z轴方向的转动，限制后点的X、Y、Z轴方向的移动和绕X、Y轴方向的转动，施加边界条件后进行有限元分析。

1.2 结果分析

(1)最大垂直力工况。在该工况下，悬架只受垂直力作用，在该力作用下，下摆臂正好绕副车架旋转，因此受到的应力小，与实际相符，其应力云图如图3所示，变形图如图4所示。在下摆臂外点与球铰座相连处有微小应力集中现象，但不超过材料的许用应力，满足强度要求。

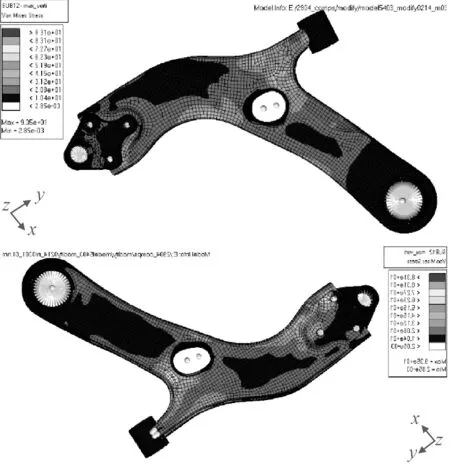
图3 最大垂直力工况应力云图

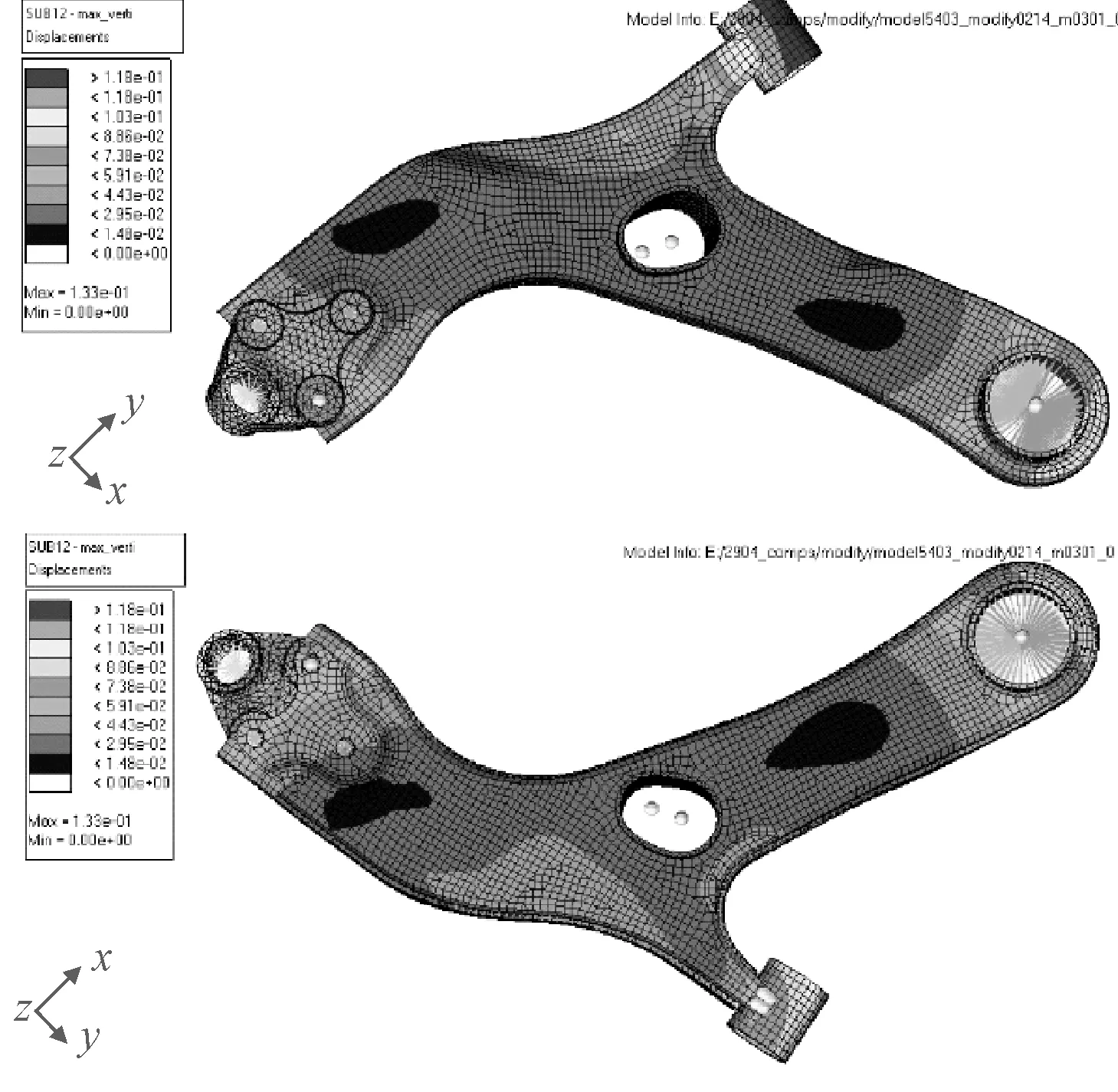
图4 最大垂直力工况变形图

(2)最大侧向力工况。在该工况下的应力云图和变形图如图5和图6所示，其最大应力为93.5 MPa，在靠近下摆臂前点有应力集中，该位置曲面有一定的弧度变化，并受到弯矩作用，出现大的应力。其他部位应力平滑过渡，总体所受应力较小。由于侧向力和垂直力的作用，下摆臂会绕副车架做微小转动，致使前点和外点的位移量较大。

图5 最大侧向力工况应力云图

图6 最大侧向力工况变形图

(3)最大制动力工况。在该工况下的应力云图和变形图如图7和图8所示。

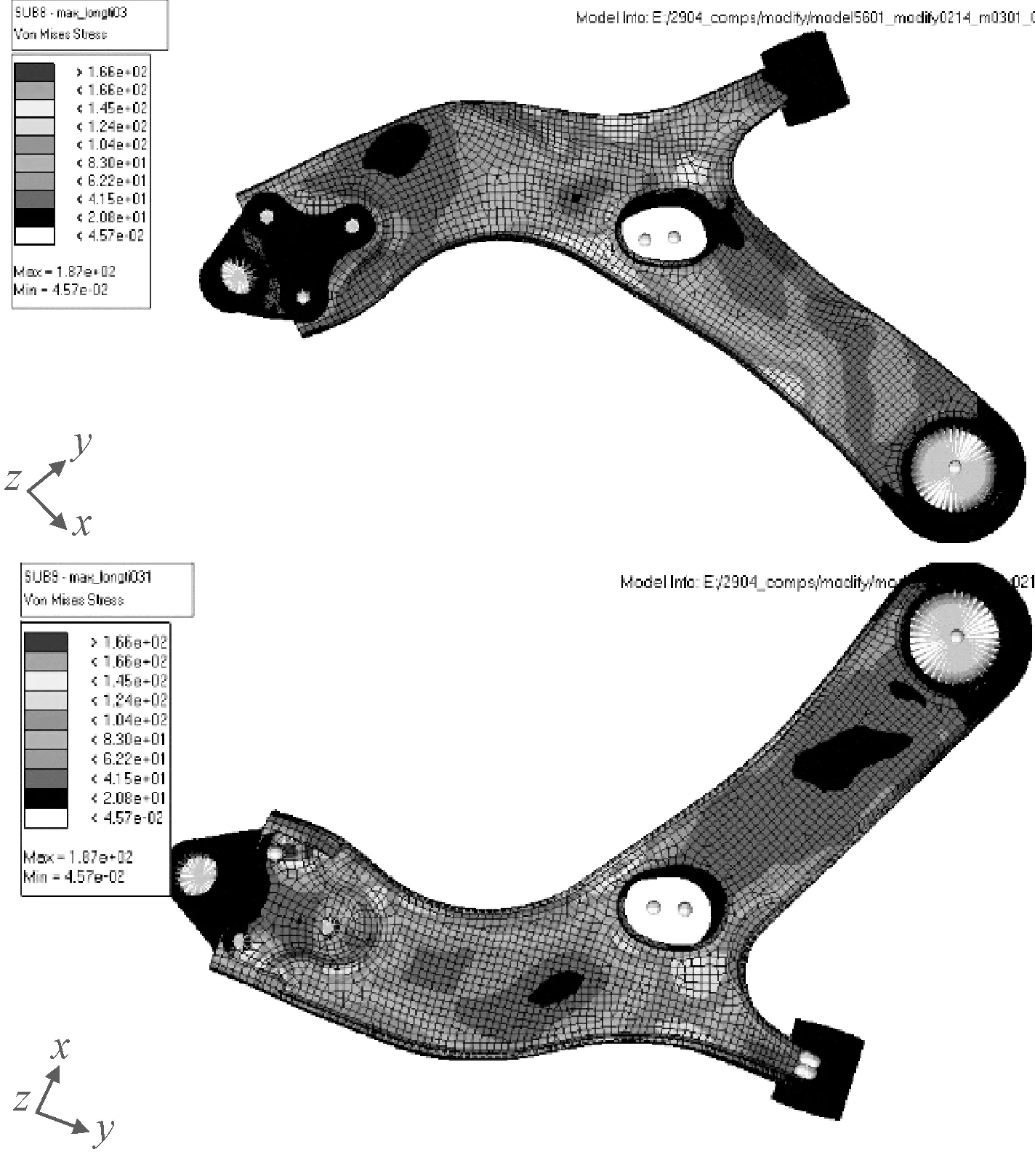
图7 最大制动力工况应力云图

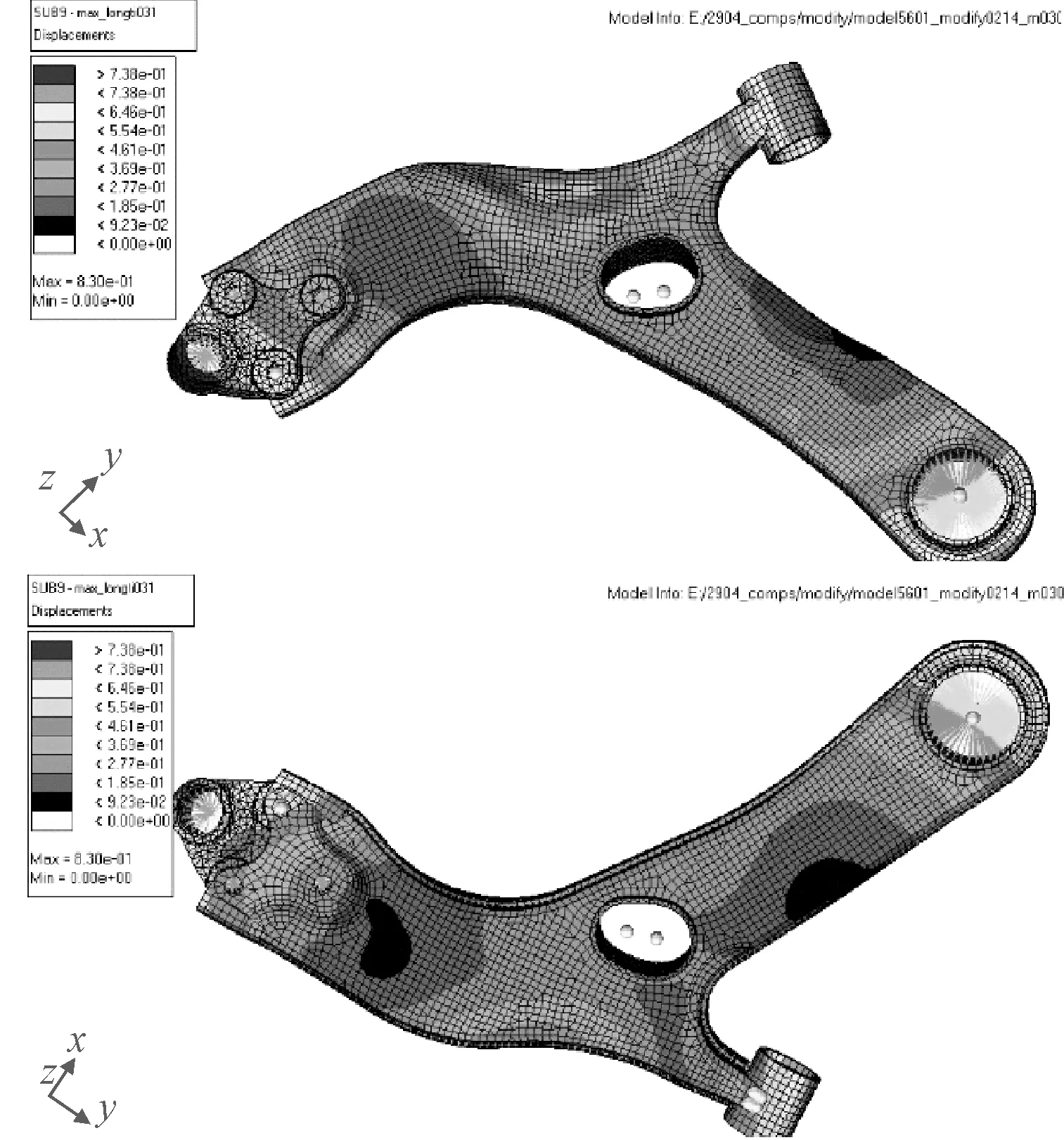
图8 最大制动力工况变形图

从以上3种工况下的应力云图可以看出下摆臂在受到极限工况时的应力分布情况，下摆臂的主体芯部等区域的应力很小，基本不承受载荷。因此，该部位还有一定的材料冗余，可进行下一步的结构轻量化优化设计。

2 下摆臂结构优化

以多工况结构加权应变能为目标函数，对下摆臂进行拓扑优化，得到下摆臂的优化轮廓结构。再根据拓扑优化结果，对优化后的模型进行几何重构及改进，最后对重构后的下摆臂进行尺寸优化。

2.1 拓扑优化

在拓扑优化中，取下摆臂模型中的相对密度Xe作为拓扑优化的设计变量，Xe的值在0与1之间连续变化，其中0定义为空，1定义为实体，0～1之间为中间密度。

2.1.1 建立静态应变能的拓扑优化模型

根据折衷规划法理论解决静态多工况的应变能优化问题[12]，目标函数为:

(1)

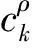
2.1.2 等值面云图

密度阈值分别取0.3、0.4、0.5、0.6，图9～图12分别为相对密度值大于0.3、0.4、0.5、0.6时下摆臂的拓扑结构。经过对比分析，相对密度值Xe大于0.5时下摆臂具有相对清晰的拓扑结构，并选择此结构作为详细优化设计阶段模型的基本结构。

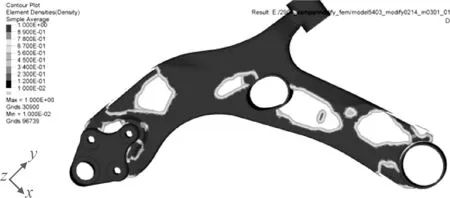
图9 相对密度值大于0.3的下摆臂拓扑结构

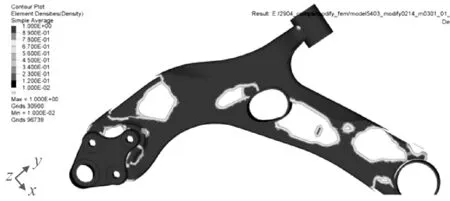
图10 相对密度值大于0.4的下摆臂拓扑结

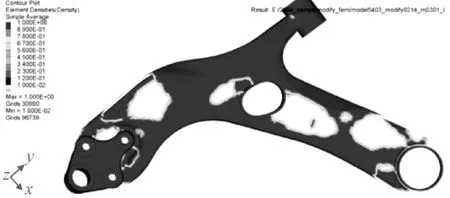
图11 相对密度值大于0.5的下摆臂拓扑结构

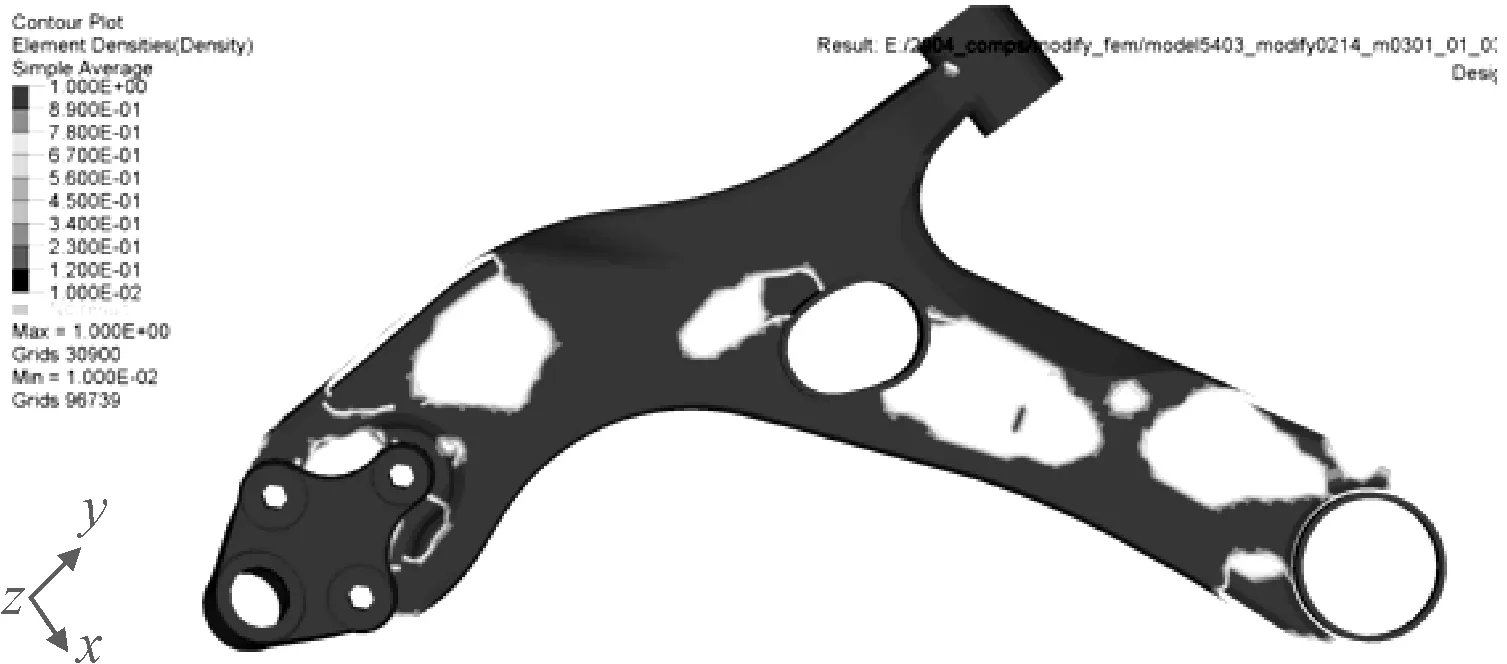
图12 相对密度值大于0.6的下摆臂拓扑结构

2.1.3 结构改进

根据优化结果可知，浅色区域是可以去除材料的，由于下摆臂是冲压板件焊接组合而成，因此对上下板的中间主体结构采用打孔的方式去除材料，可以达到减重的目的，改进方案模型如图13所示。

图13 改进方案模型

2.2 下摆臂尺寸优化

以重构后下摆臂有限元模型为研究对象，施加与原结构相同的载荷约束等边界条件，在Optistruct中进行尺寸优化，以壳单元厚度为设计变量，结构质量和模态分析结果、下摆臂在各工况下所受的应力为分析对象，并采用将第一级优化(拓扑优化)的结果作为第二级优化(尺寸优化)约束的多级容差序列法来优化。选取容差系数为0.35、0.45、0.55分别进行计算。经模态分析可知，第7阶固有频率远大于共振频率，只需将其作为约束条件进行限制。同时保证下摆臂在3种工况下的应力小于许用应力值。故约束条件为：

(2)

式中：ci为第i个工况的下摆臂应变能；c*为拓扑优化得到的最小加权应变量；σi为第i个工况的下摆臂应力，取i=1,2,3，分别为最大垂直力工况、最大侧向力工况和最大制动力工况；[σ]为许用应力；ξ为容差系数，分别取0.35,0.45,0.55。优化结果如表2所示。

表2 3种优化结果的比较

ξ=0.45和ξ=0.55的优化结果相同，ξ=0.35与ξ=0.45的差异也很小，说明此时ξ的变化对尺寸优化影响不大，最终选取ξ=0.45的优化结果。

3 优化前后下摆臂性能分析与对比

3.1 优化前后装配说明与质量对比

优化后去除了下摆臂部分材料，减轻了质量，但其各个连接点与装配位置的结构并无改变，因此装配方式也没有改变，各个部件的布置不会存在干涉问题；优化前的总质量为3.404 kg。下摆臂的上下板经过拓扑优化和尺寸优化后的质量约为3.125 kg，故优化后质量减轻了0.279 kg，减少了8.2%，达到了减重的目的。

3.2 优化后的下摆臂模态分析

优化后下摆臂的各阶振型的频率值如图14所示，从图14可知，前六阶的频率较小，视为刚体运动，第7阶固有频率值为671.86 Hz，其后的各阶频率逐渐增大，并且第7阶固有频率远大于共振频率，故不会发生共振现象，保证了下摆臂的动态特性。

图14 下摆臂自由模态分析各阶频率值

3.3 优化后的下摆臂结构强度与刚度分析

对优化后的下摆臂同样在3种极限工况下、施加相同载荷进行有限元分析，获得的强度刚度结果如图15～图20所示。

(1)最大垂直力工况应力云图和变形云图如图15和图16所示。

图15 最大垂直力工况应力云图(最大应力为91.1 MPa)

图16 最大垂直力工况变形云图(最大变形量为0.138 mm)

(2)最大侧向力工况应力云图和变形云图如图17和图18所示。

图17 最大侧向力工况应力云图(最大应力为111 MPa)

图18 最大侧向力工况变形云图(最大变形量为0.244 mm)

(3)最大制动力工况应力云图和变形云图如图19和图20所示。

图19 最大制动力工况应力云图(最大应力为192 MPa)

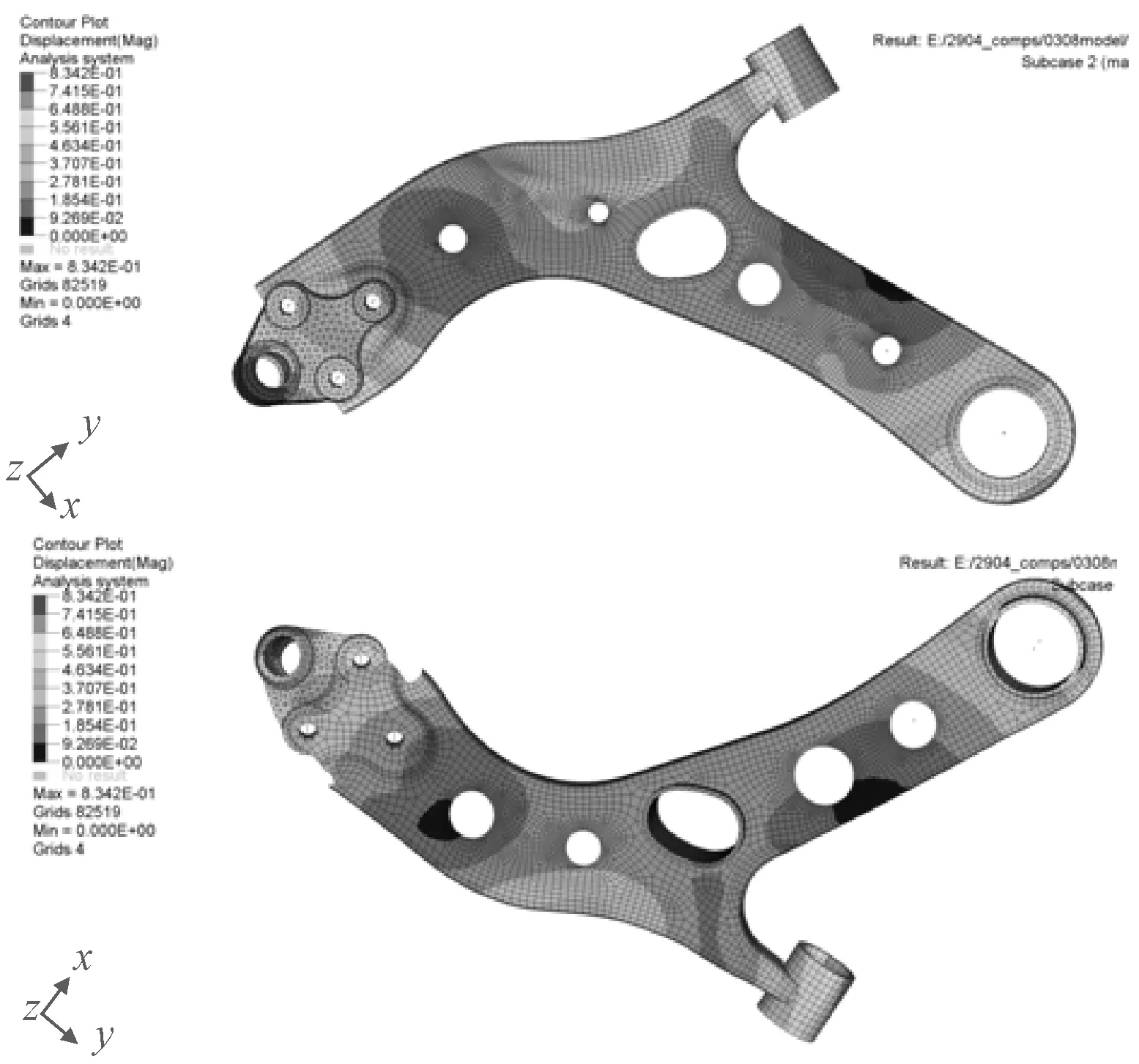
图20 最大制动力工况变形云图(最大变形量为0.834 mm)

从以上3种工况下的应力云图和变形云图来看，在孔周围无集中应力，且孔周围应力不大，在该位置打孔对结构强度影响不大，能达到轻量化目的。较大应力主要分布在上板和下板的边缘，最大应力主要集中在上下板与球铰座连接处，也在应力要求范围内。下摆臂的最大变形量都小于1 mm，整体变形很小，结构具有良好的刚度性能。

4 结论

笔者对SUV汽车悬架下摆臂进行了有限元分析，并对其进行了结构优化，包括拓扑优化及尺寸优化。通过结构优化，减轻了下摆臂的重量，并通过对优化后的结构进行各项性能分析得知，其满足实际要求，保证了结构的强度和刚度及其动态特性。