基于响应曲面法的曲面抛光工艺参数研究

陈满意,樊江龙,林文访

(武汉理工大学 机电工程学院，湖北 武汉 430070)

自由曲面零件以其优良的空气动力学、流体动力学和热力学等特性大量使用在模具、汽车零部件、航空航天和船舶等领域。自由曲面使得模具结构更加紧凑，减轻了模具的质量，延长了模具的寿命。据统计模具加工周期中，表面抛光时间占总加工时间的30%～50%[1]。目前，曲面零件的抛光仍然主要依赖于手工作业，存在效率低、耗时长、不能保证加工质量等缺点。国内外针对曲面零件自动抛光技术的研究[2]取得大量成果，但目前涉及机器人曲面零件抛光工艺参数的研究以及粗糙度预测还是不多。陈国达等[3]采用气囊抛光，提出区分不同抛光阶段来选择磨料粒度的工艺规划方法，通过试验验证了该工艺方法的优越性，取得了较好的抛光效果；Zhao等[4]通过建立砂轮表面数字化仿真模型以及分析磨粒的运动轨迹对BK7 光学玻璃的超声振动磨削加工建立了表面粗糙度预测模型；Arunangsu等[5]应用Box-Behnken设计和响应曲面法对线切割加工的CP-Ti粉末冶金零件建立表面粗糙度预测模型;Senthil等[6]采用改进的粒子群算法建立前馈神经网络模型，该模型可有效地降低粗糙度预测误差。

曲面抛光工艺由抛光平台、抛光工具、工件材料、抛光工具材料、抛光系统等众多因素[7]决定。工艺参数主要由抛光力、抛光刀具的转速、抛光工具材料等组成，是否选择最优工艺参数组合直接关系到抛光效率高低和抛光质量的好坏[8]。笔者采用球形刀具，利用6自由度工业机器人平台和自主开发的控制软件来搭建具有恒力控制功能的抛光控制系统试验平台完成曲面零件抛光工艺参数优化的研究，使用响应曲面法对抛光工艺参数进行回归分析，建立表面粗糙度预测模型获得每道工序的最优工艺参数组合，实现对抛光表面质量和抛光效率的控制，改变目前严重依赖人工抛光的现状。

1 抛光试验

1.1 抛光机理

抛光机理的研究是分析抛光质量影响因素的重要部分，笔者采用球形磨头对零件型腔抛光，因此有必要针对球形磨头的抛光机理进行研究分析。材料去除量与各工艺参数的关系可以采用Preston模型来描述球形磨头抛光过程,Preston函数方程为：

(1)

式中：dH(x,y)/dt为材料平均去除率；k为压力和速度之外的综合影响系数；P(x,y)为接触区域内的抛光压力；v(x,y)为接触点处刀具与零件的相对速度。

由Preston函数方程可以得出材料去除率与接触区域内的压力和相对速度成正比。由赫兹接触理论可得接触区域压力分布方程式(2)。

(2)

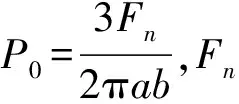
通过式(2)可求出球形磨头对型腔曲面零件抛光时在接触区域的抛光压力分布函数，现需要知道在接触区域内的速度分布函数，接触区域内的速度分布与刀具转速、刀具姿态和刀具尺寸有关[9]。设刀具的角速度为ω，其矢量表示为:

ω=ω(sinσ,0,cosσ)

(3)

向量r为球形磨头半径矢量，即：

r=(x,y,-h)

(4)

接触区域内产生的速度矢量记作vp，即：

vp=ω×r

(5)

根据推导出来的接触区域速度分布函数和压力分布函数可以得到球形磨头的材料去除函数如下：

(6)

在抛光工艺研究中，材料去除量对抛光质量有很大的影响。由式(6)可得，使用球形磨头对型腔曲面进行抛光时，影响材料去除量的因素有接触压力、刀具转速、刀具轴线与接触面法线夹角、刀具材料、工件材料、刀具与曲面等效曲率半径等。

1.2 搭建试验平台

在对抛光工艺和抛光机理进行分析的基础上，搭建试验平台进行抛光工艺试验。影响抛光的因素众多，这里采用单因素试验的方法研究工艺参数中的主要影响因素：刀具转速、进给速度、接触压力和轨迹行距。

试验使用的硬件设备包括工业机器人本体、NI PCIe-6320数据采集卡、信号放大器、E550-2S0004(B)变频器、ME3DT120三轴力传感器、电主轴及连接装置、控制柜、上位机、时代TR210手持式粗糙度测量仪、抛光磨头、抛光介质、待抛光工件(凹形柱面零件)，试验硬件设备如图1所示。

图1 实验硬件设备

除使用图1所示的装置外，还使用自主开发的多轴刀位点数据生成软件和机器人控制系统。在UG进行二次开发完成有限元网格生成、多轴刀位点数据自动生成和刀具轨迹规划[10-11]功能，采用等参数法[12]通过控制系统来驱动机器人完成恒力抛光[13]。

本试验待抛光工件如图2所示，材料为45钢，最终要求工件曲面表面粗糙度小于0.1 μm。由于曲面零件的前道工序为铣削，表面刀痕较深，经测量表面粗糙度在3～6 μm之间，质量较差，为达到超精细抛光目的，制定3道工序对其进行打磨。①粗抛。采用球形砂轮磨头进行加工，主要作用是快速除掉铣削工序中的刀痕；②半精抛。采用弹性球形磨头，主要作用是去除粗抛划痕，为精抛打基础；③精抛。采用羊毛球形磨头配合研磨膏，达到超精抛光甚至镜面效果。

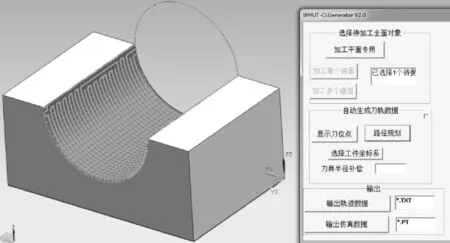
图2 待抛光工件的多轴刀位点数据生成界面

1.3 单因素试验

零件的抛光工艺试验先进行平面单因素试验，然后根据单因素试验结果来设计曲面零件复合试验，这样不仅可以减小试验组数而且可以获得较精确的最优工艺参数组合。平面试验采用球形刀具进行抛光不仅效率低而且刀具磨损严重，因此平面试验采用柱状尼龙刀具。在抛光前对工件抛光表面粗糙度测量3次求取平均值，抛光结束后再测量3次求取平均值，将粗糙度值改变量作为因素水平。根据试验结果可以得到刀具转速、接触压力、进给速度、轨迹行距与工件表面粗糙度的关系变化，如图3所示。

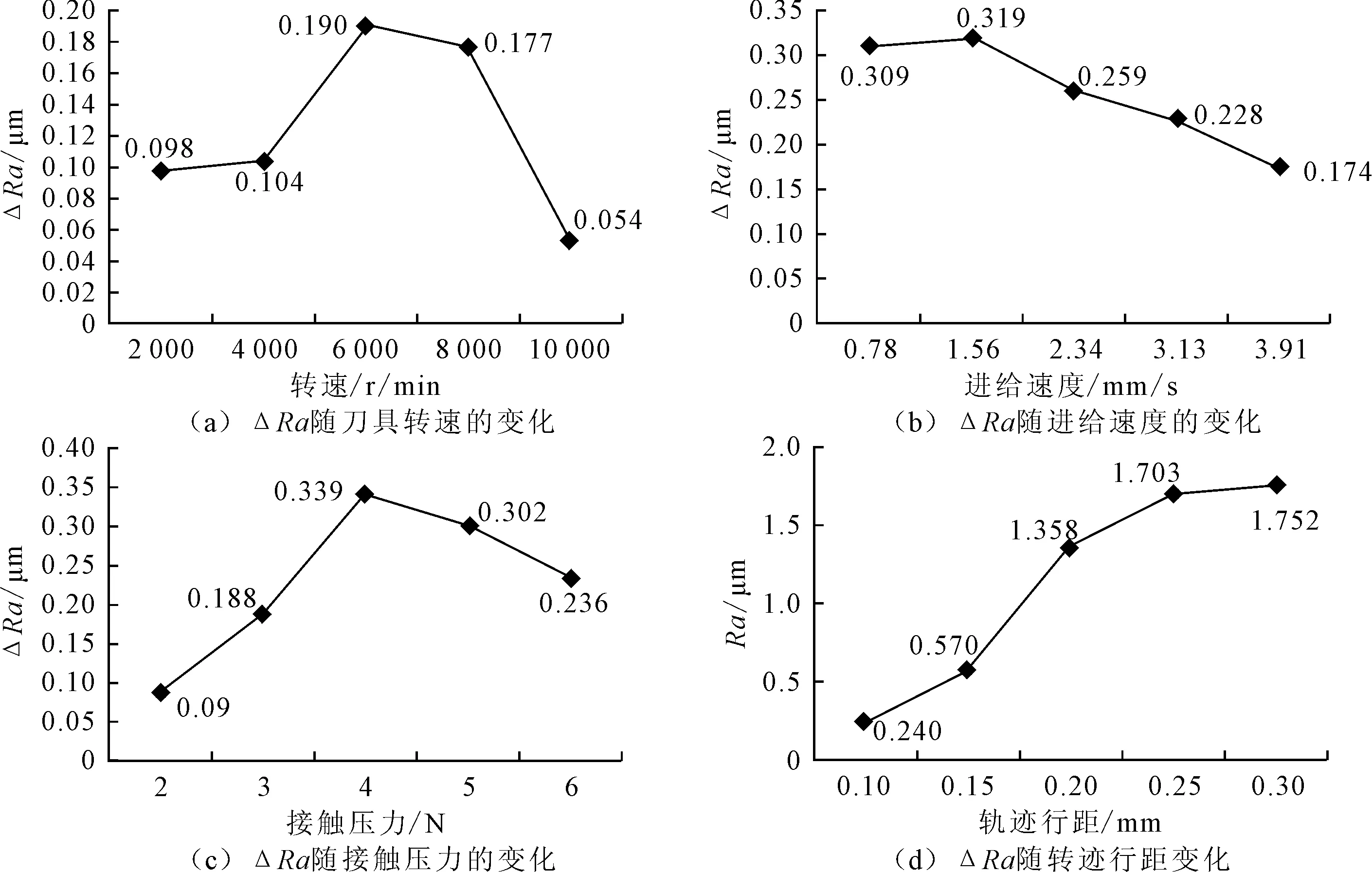
图3 关键工艺参数的单因素试验规律

由图3(a)可知，粗糙度值随着刀具转速的提高而增加，但是转速过高时变化值减小。这是因为在一定范围内，转速越高，相当于单位时间内磨削次数增加，因此表面质量更好。转速过高时，由于摩擦发热作用，在高温下，弹性刀具材料里的结合剂橡胶易发生软化现象，刀具的磨粒由于结合剂的软化与工件的接触压力将大大减小，导致磨削效果下降。

由图3(b)可知，抛光表面质量随进给速度的增大而降低。这是因为进给速度越小抛光次数越多，但在实际抛光过程中，为了保证抛光效率，进给速度应尽量提高。

由图3(c)可知，工件表面质量随接触压力的变化先逐渐增大后变小。接触压力的增大会使磨粒与接触表面作用增加，在一定范围内会获得较好的表面质量。但接触压力过大会使吃刀深度增加，导致刀痕的产生和磨粒作用力减小，最后使粗糙度值改变值较小。

由图3(d)可知，轨迹行距对抛光质量影响非常显著，选择合理抛光轨迹行距以提高抛光表面质量的同时保证抛光效率。抛光轨迹行距较小时，易导致过抛，而且会降低抛光效率；抛光轨迹行距过大时，会导致欠抛，而且会产生明显的抛光纹路，影响抛光表面质量。轨迹行距与抛光效率密切相关，轨迹行距越小获得的抛光质量越好，但抛光相同面积所花费的时间将大大增加。因此在选择轨迹行距时要综合考虑考虑抛光质量和抛光效率。

2 抛光试验结果分析

2.1 中心复合试验

抛光工艺参数有刀具转速、刀具进给速度、接触压力和轨迹行距等[14]。如果这些因素按4水平进行试验，试验组数非常多，因此合理安排试验很有必要。笔者采用基于响应曲面法中的中心复合设计建立抛光表面粗糙度预测模型，该方法是基于多元线性回归采取主动收集数据的方法得到较好的回归方程[15]。为达到最佳抛光效果并且有较高的抛光效率，对砂轮、弹性磨头和羊毛抛光分别安排中心复合试验，这里以第二道工序球形弹性磨头为例进行说明。根据单因素试验结果，将各因子的取值范围定为：刀具转速5 000～9 000 r/min,接触压力4～6 N，轨迹行距0.1～0.5 mm，进给速度3.13～6.25 mm/s。对凹形柱面工件使用机器人系统进行抛光试验。试验安排如表1所示。

由于前道工序获得粗糙度值一致性较好，因此表1中测量得到的粗糙度值，可作为粗糙度预测模型的响应值。

2.2 粗糙度预测模型的建立和验证

表面粗糙度受众多抛光工艺参数耦合作用影响，预测模型非线性，一般采用二阶模型，粗糙度预测模型如下：

(7)

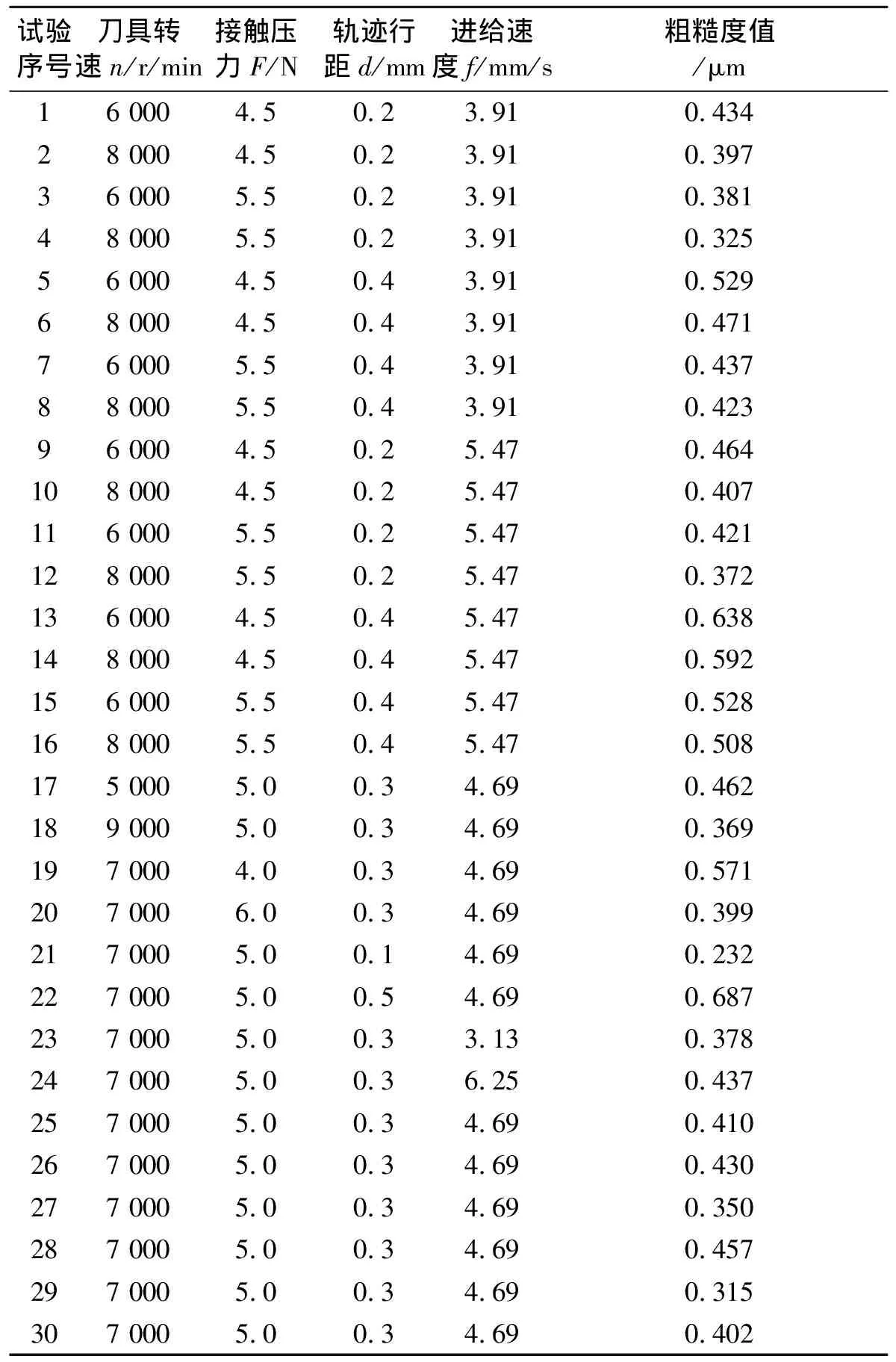
表1 中心复合试验设计安排表

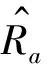
将表1试验结果在Design Expert软件中进行方差分析，为提高模型的可靠性，一般需要剔除模型中的不显著因子。根据逐步选择法思想对模型中的因子进行剔除，由此获得预测模型，其参数如表2所示，其结果用来判断预测模型的准确性。由表2可知，模型的F值为15.76，P值远远小于0.000 1，说明该模型较为显著。表2中失拟检验F值为0.56，P值为0.829 5，说明该模型失拟不显著。求得试验样本标准差值为0.043,平均值为0.44，变异系数为9.68，预测残差平方和为0.11,R2值为0.857 2，校正R2为0.802 8,预测R2为0.600 4，说明试验结果和预测值比较接近。信噪比为13.863，本模型有效的情况下，要求信噪比大于4。根据这些对模型评价的指标，可得建立的粗糙度预测模型能够实现精度较高的预测效果。

在对模型整体预测效果分析后，需对模型中的因子进行显著性分析，剔除不显著因子。预测模型中的单因子如刀具转速、接触压力、轨迹行距、进给速度对响应值都是显著的，因此都应保留。而因子交互作用响应值Fd和和df并不显著，但是相对于其他因子交互组合，其显著性较高，为便于研究交互项，选择保留显著度最高的df交互项。最后根据因子实际值得到的预测模型如下：

Ra=3.371 81-2.179 17×10-5n-

1.019 98F-1.321 25d-0.032 292f+

0.223 56df+0.094 656F2+1.728 91d2

(8)

试验测试值与预测值的关系如图4所示。由图4可知，试验测量值在模型的预测线附近，因此模型是有效的。

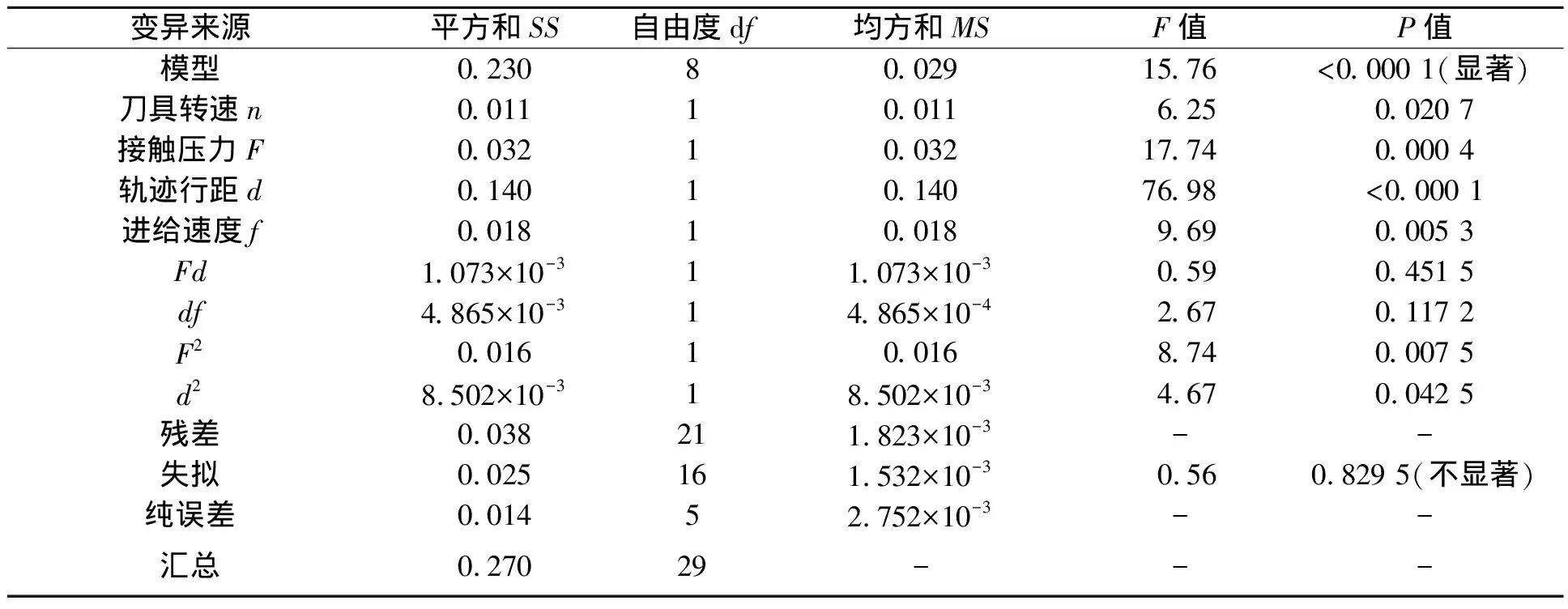
表2 试验方差分析

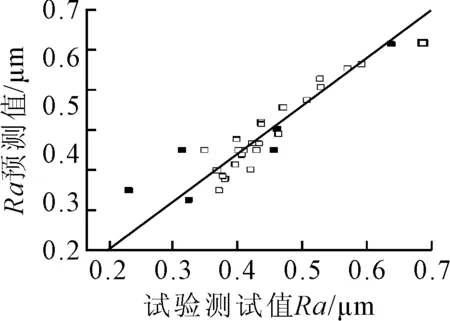
图4 试验测试值与预测值的关系

为验证模型预测精度，在模型的参数值变化范围内进行试验来检验预测模型的精度，试验结果如表3所示。

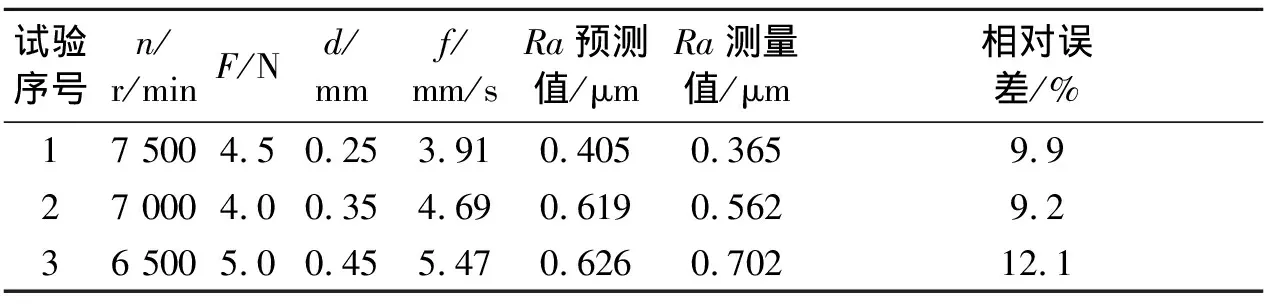
表3 预测值与试验结果对比

由表3可知，在误差允许的范围内，预测模型能够达到预测的目的。

2.3基于曲面响应法的工艺参数研究

图5、图6是抛光工艺参数中轨迹行距与进给速度对Ra值响应曲面图和等高线图。由图5可知，该响应面曲率较小，这与表3中轨迹行距和进给速度交互作用显著性较差有关。由图5可知，Ra值随进给速度的减小而减小，在轨迹行距为0.20 mm时，Ra值变化速度较小，在轨迹行距为0.40 mm时，Ra值变化速度较大，且Ra值随轨迹行距的减小而减小。由图6可知，在轨迹行距较大时，响应值Ra变化较大。由此判断，最优点应该在轨迹行距为0.20 mm和进给速度取3.91 mm/s时的位置。

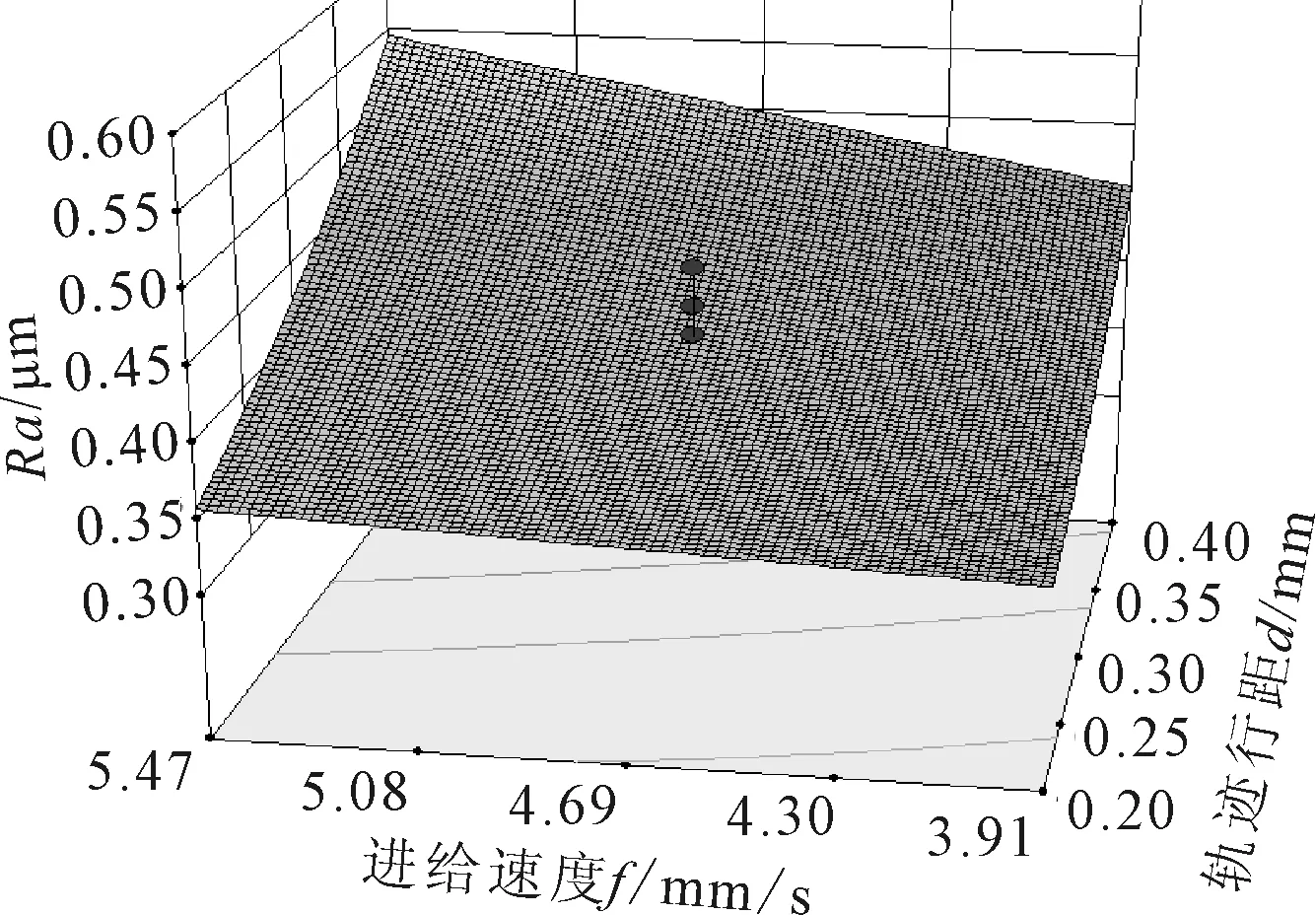
图5 轨迹行距与进给速度交互作用响应曲面图

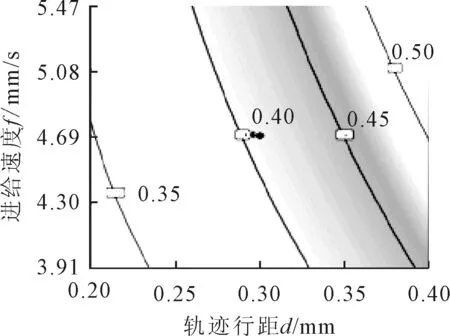
图6 轨迹行距与进给速度交互作用等高线图

在本预测模型因子变化范围内，根据曲面响应模型对工艺参数进行优化，首先将响应值最小设为目标，然后使用Design-Expert软件进行优化，在设置好初始条件后，使用合意度最大来得到最优参数组合。得到5组优化的参数组合，如表4所示。

表4 优化的参数组合

根据表4可得弹性球形磨头最优的工艺参数组合为：刀具转速为6 000 r/min,接触压力为5.39 N，轨迹行距为0.2 mm,进给速度为3.91 mm/s。使用这组抛光工艺参数抛光后，经过3次测量后取平均值得到粗糙度值为0.381 μm，误差值为10.09%，说明该明预测模型可靠性较高。

3 试验验证

根据弹性磨头中心复合试验结果，采用最优的工艺参数组合对曲面零件进行抛光可显著提高表面质量。类比弹性磨头试验，砂轮磨头及羊毛磨头同样采用响应曲面法以提高表面质量和抛光效率为目标得到最优工艺参数。最终抛光工艺参数为：第一道工序使用球形砂轮抛光，刀具转速为2 000 r/min, 接触压力为2 N，轨迹行距为0.5 mm,进给速度为7.81 mm/s。第二道工序使用弹性磨头，刀具转速为6 000 r/min,接触压力为5.39 N，轨迹行距为0.2 mm,刀具进给速度为3.91 mm/s时，可获得较好的抛光效果。第三道工序抛光工艺参数为：刀具转速为8 000 r/min,接触压力为3 N，行距为0.4 mm,进给速度为7.03 mm/s,研磨膏粒度为8 000目。使用TR210手持式粗糙度测量仪，如图7所示。在工件分割线左侧加工表面依次选取6点垂直抛光轨迹方向测量粗糙度值，求取平均值作为最终结果，分割线右侧为未加工表面同样取6个点测粗糙度求平均值作为对照。

图7 粗糙度测量点分布图

经测量可得，未抛光时工件曲面粗糙度在3.038～4.534 μm，粗糙度均值为3.789 5 μm；经过第一道工序砂轮抛光，表面粗糙度降低到1.215～1.903 μm，粗糙度均值为1.448 7 μm；经过第二道工序弹性球形磨头抛光，表面粗糙度降低到0.353～0.412 μm，粗糙度均值为0.381 3 μm；经过第三道工序羊毛磨头+研磨膏抛光，表面粗糙度降低到0.019～0.041 μm，粗糙度均值为0.033 2 μm，达到镜面效果。由此可知，使用优化的工艺参数可以显著降低曲面粗糙度，满足表面粗糙度小于0.1 μm的质量要求。

4 结论

(1)根据抛光机理，分析了球形磨头材料去除量与各工艺参数的关系，搭建机器人恒力抛光试验平台，进行单因素试验,分析影响抛光质量的工艺参数。获得关键工艺参数的最佳水平范围。

(2)抛光工艺参数回归分析。参考单因素试验得到的抛光工艺参数水平范围，使用曲面响应法建立粗糙度二阶预测模型。通过对模型显著性、失拟和准确性进行分析和试验验证，证明模型的精度较高。

(3)由于工件曲面的前道工序为铣削加工，表面刀痕较深，为达到超精加工的目的，需使用3道工序对其进行抛光，对3道工序分别进行中心复合试验。根据建立的预测模型对抛光工艺参数进行优化，使用每道工序的最佳参数水平组合对工件进行抛光，试验结果获得镜状光泽面，说明该预测模型及优化的工艺参数可明显提高工件表面质量。