旋转变换贯通思路，同类呈现加深理解——从两道较难考题的思路说起

筅江苏省江阴市华士实验中学 赵丹农

最近笔者在某校八、九年级两份阶段试卷看到两道本质类似的考题，都需要通过旋转变换进行思路突破，实现解决.但是在一些解题研究的QQ群里，有不少老师仍然在求助解法，笔者感觉有必要做些关联式讲评，于是将这两道习题设计成同类习题微教学，在班级讲评之后，取得了较好的效果.本文先给出这两道较难习题的思路分析，再跟进教学微设计及教学立意的解读，供研讨.

一、两道较难考题的思路解析

考题1：（某校八年级下学期阶段检测卷，填空较难题）如图1，点C为线段AB的中点，E为直线AB上方的一点，且满足CE=CB，连接AE，以AE为腰、A为顶角的顶点作等腰Rt△ADE，连接CD，当CD最大时，∠DEC= .

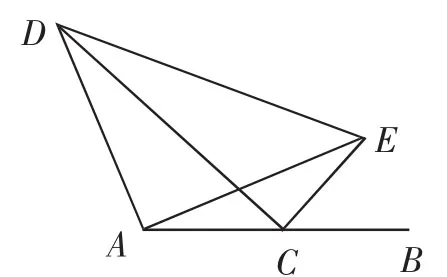
图1

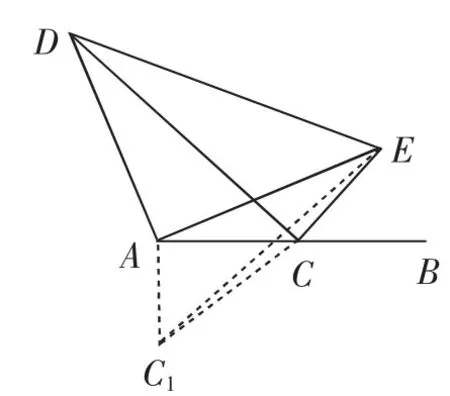
图2

思路1：如图2，将△ADC绕点A顺时针旋转90°得△AEC1，点D、E重合，点C对应着C1，连接CC1（或以A为顶点，AC为直角边，在AC的下方作等腰直角△ACC1）.

则△ADC △AEC1.则CD=EC1，AC=AC1.

在△ECC1中，EC1＜EC+CC1.则只有当E、C、C1共线时，EC1的值最大，即CD最大.

由AC=AC1，得∠ACC1=45°，则∠ACE=135°.

由点C为线段AB的中点，得CA=CB.又CE=CB，则CE=CA.则∠AEC=22.5°.

在等腰Rt△ADE中，∠AED=45°.则∠DEC=67.5°.

思路2：如图3，将△ACE绕点A逆时针旋转90°得△ADE1（点E与点D对应），连接CE1（或以A为顶点，AC为直角边，在AC的上方作等腰直角△ACE1）.

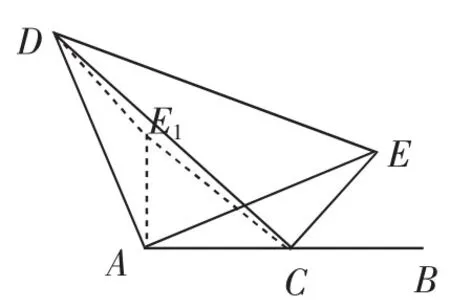
图3

则△AEC △ADE1.则AC=AE1，∠AEC=∠ADE1.在△DCE1中，CD＜CE1+DE1.

则只有当D、C、E1三点共线时，CD最大.

由AC=AE1，得∠AE1C=45°，则∠AE1D=135°.

由点C为线段AB的中点，得CA=CB.又CE=CB.则CE=CA.则DE1=AE1.则∠ADE1=∠AEC=22.5°.又等腰Rt△ADE中，∠AED=45°，则∠DEC=67.5°.

考题2：（某校九年级下学期阶段检测卷，填空较难题）如图4，P是半圆O上一点，Q是半径OA的延长线上一点，AQ=OA=1，以PQ为斜边作等腰直角三角形PQR，连接OR，则线段OR的最大值为 .

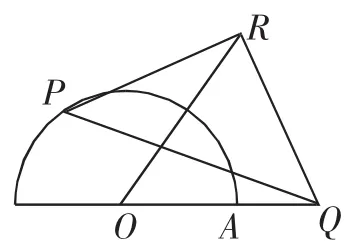
图4

图5

思路1：如图5，将△ROQ绕R点顺时针旋转90°，得到△RO1P，连接PO、RO1、OO1、OP（或以R为顶点，RO为直角边，在RO的上方作等腰直角△ROO1）.

在△POO1中，OO1＜PO+PO1.则只有当P、O、O1三点共线时，OO1最大.

由△ROO1为等腰直角三角形，得OR=

此时，OO1=PO+PO1=1+2=3.

思路2：如图6，将△ROP绕R点逆时针旋转90°，得到△RQO1，连接PO、RO1、OO1、QO1（或以R为顶点，RO为直角边，在RO的下方作等腰直角△ROO1）.

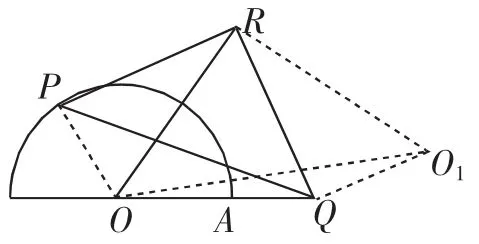
图6

则△ROP △RO1Q，则QO1=OP=1.

在△QOO1中，OO1＜QO+QO1.则只有当Q、O、O1三点共线时，OO1最大.

由△ROO1为等腰直角三角形，得OR=

此时，OO1=QO+QO1=2+1=3.则OR=

二、同类习题的微教学设计

问题1：如图7，△ABC与△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，连接BE、DC.

（1）探究CD、BE的数量关系与位置关系；

（2）连接CE，求证：线段AC、CE的长度之和不小于CD的长.

设计意图：先以两个共顶点的等腰直角三角形的一道经典习题训练学生，为后续研究提供思路上的启示.

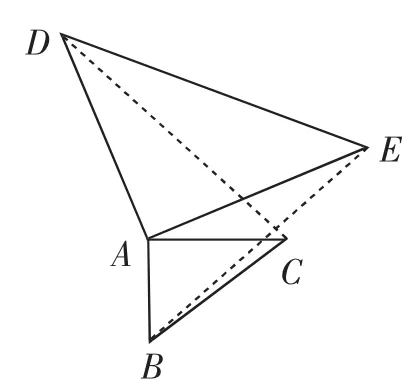
图7

问题2：如图1，点C为线段AB的中点，E为直线AB上方的一点，且满足CE=CB，连接AE，以AE为腰、A为顶角的顶点作等腰Rt△ADE，连接CD.

（1）求证CD≤AC+CE；

（2）当CD最大时，求∠DEC的度数.

设计意图：考虑到与问题1保持一定的连续性，在上文“考题1”基础上，设计了铺垫式问题，讲评时注意启发学生不同的旋转变换的解法（如上文中两种思路）.

问题3：如图4，P是半圆O上一点，Q是半径OA的延长线上一点，AQ=OA=1，以PQ为斜边作等腰直角三角形PQR，连接OR，探究线段OR的最大值.

设计意图：问题3直接使用“考题2”，不预设铺垫，安排学生挑战难题，而且有两种不同的旋转构图的方法，教学时注意启发学生从不同的角度进行构图、推理.

三、关于同类习题的教学思考

1.重视跨年级研究习题，收集“关联”习题

教师在各自年级任教时往往眼之所及都是本年级的习题，特别是有些教师多年任教同一年级，往往缺少对其他年级习题的关注.我们认为，教师研究解题不能囿于任教年级，因为习题的结构或解题策略有时会在不同年级的习题中得到体现，如果教师能跨年级研究习题、收集“关联”习题，并将问题变式、拓展，对于开阔学生眼界、启发学生打开思路是十分重要的.

2.要精选“关联”习题，预设同类习题教学

教师注意跨年级研究习题之后，将收集到的“关联”习题进行恰当的重组，在备课选题时加强同类习题的链接与变式，以题组呈现的方式开展解题教学，往往能取得较好的解题教学效果，并且能促进学生识别同类问题，对相同结构问题的理解走向深入.像上文两道较难题，如果孤立地在八年级时练过一次，到九年级时学生再遇到很容易遗忘，从而找不到思路，这时如果能链接式讲评，八年级的学生印象就会很深.也许有老师说，学生在八年级时还不宜超前接触有关圆的习题，讲了是不是超标教学、超前教学？事实上并不是这样的，因为考题2本质上并不涉及圆的更多性质，只是利用圆的半径相等这个简单性质，小学生都知道.

3.难题求解要一题多解，教学时要多题归一

教师在研究习题解法时，针对难题求解要追求一题多解，尽可能从不同角度突破思路，并且思考哪种解法是最简单、最自然、最初等的解法（倡导回到核心概念去解题），这样在解题教学时就能驾驭不同的教学生成，因为学生的解法可能会多种多样，如果教师课前没有深入思考可能的解法与思路，教学现场对有些独特的解法进行准确理解和恰当评析就会有很大的挑战，有时就容易听不清、想不明，造成误判，或评价“不作为”.当然，作为教师，在较难题的多解之后，还可引导学生加强解后反思与回顾，思考“殊途何以同归”，即多解归一，这样可以有效达成学生解一题、会一类的效果.